5.5 Heron的公式

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 海隆的方程式

  Collapse Expand

  海隆的方程式

  播放段落

  You are in History class learning about different artifacts from other cultures, when the subject of pyramids is presented by your teacher. He informs the class that pyramids come in a variety of sizes, designs, and styles, and are found not only in Egypt, but in many other countries around the world. He tells everyone that a typical pyramid might be approximately 200 meters long at the base and 175 meters up each of the diagonal sides.
  ::您正在历史课学习来自其他文化的不同文物, 当您的老师介绍金字塔的主题时。 他告诉该课金字塔的大小、设计和风格各不相同, 不仅在埃及, 而且在世界上许多其他国家都有。 他告诉大家典型的金字塔在基底大约200米长, 在对角两边各175米宽。

  播放段落

  Your mind wanders back to your math class from that morning, and you find yourself wondering if there is a straightforward way to determine the area of one of the faces of the pyramid from the information you have been given.
  ::从那天早上起,你的头脑又回到你的数学课, 你发现自己在想是否有直截了当的方法 从你得到的信息中 确定金字塔面部的面积。

  播放段落

  Do you think there is a way to do this?
  ::你认为有办法这样做吗?

  播放段落

  Heron's Formula
  ::海隆的方程式

  播放段落

  One way to find the area of an oblique triangle when we know two sides and the included angle is by using the formula $\begin{align*}K = \frac{1}{2} \ bc \sin A\end{align*}$ . We could also find the area of a triangle in which we know all three sides by first using the to find one of the angles and then using the formula $\begin{align*}K = \frac{1}{2} \ bc \sin A\end{align*}$ . While this process works, it is time-consuming and requires a lot of calculation. Fortunately, we have another formula, called Heron’s Formula, which allows us to calculate the area of a triangle when we know all three sides. It is derived from $\begin{align*}K = \frac{1}{2} \ bc \sin A\end{align*}$ , the Law of Cosines and the Pythagorean Identity .
  ::当我们认识两边和包含角度时,找到斜方三角形区域的一个方法就是使用公式 K=12 bcsinA。 我们还可以找到一个三角形区域,在这个三角形中,我们首先通过找到一个角度,然后使用公式 K=12 bcsinA 来找到所有三方。 虽然这一过程有效,但它耗时且需要大量计算。 幸运的是,我们还有另一个公式,叫做Heron的公式,它允许我们在认识所有三面时计算三角形区域。 它来自K=12 bcsinA、Cosines法和Pythagorean 身份。

  播放段落

  $\begin{align*}K = \sqrt{s(s - a)(s - b)(s - c)}\end{align*}$ where $\begin{align*}s =\frac{1}{2}(a+b+c)\end{align*}$ or half of the perimeter of the triangle.
  ::在s=12(a+b+c)或三角形半边角的Ks(s-a)(s-b)(s-c)处。

  播放段落

  Finding the Area of a Triangle 
  ::查找三角区域

  播放段落

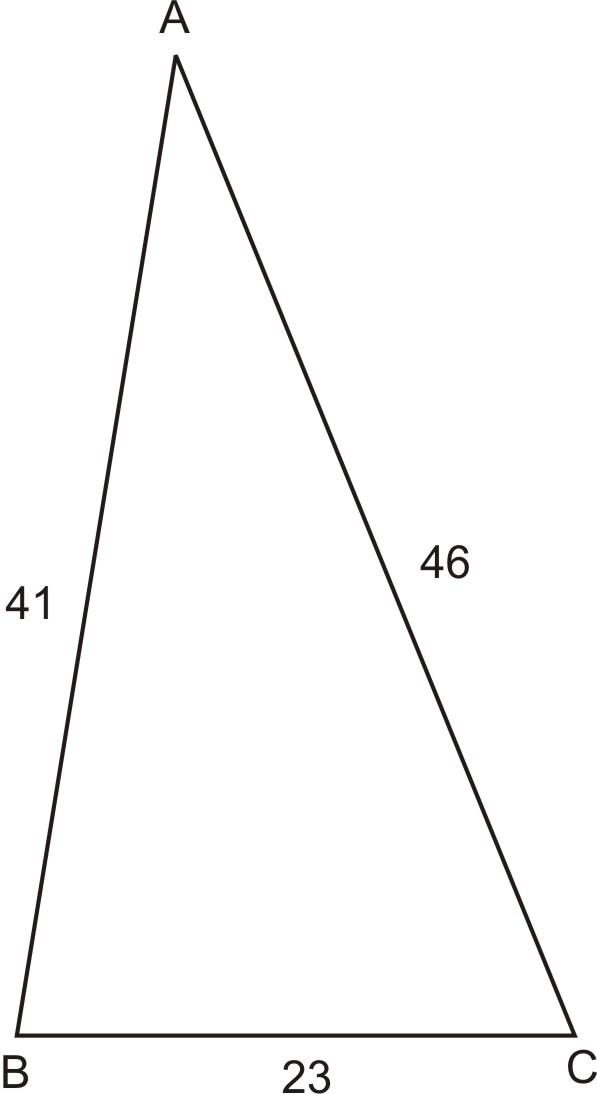
  1. In $\begin{align*}\triangle{ABC}, a = 23, b = 46\end{align*}$ , and $\begin{align*}c = 41\end{align*}$ . Find the area of the triangle.
  ::1. 在 ABC, a=23, b=46, c=41。 查找三角形的区域 。

  

  播放段落

  First, you need to find $\begin{align*}s\end{align*}$ : $\begin{align*}s = \frac{1}{2}(23 + 41 + 46) = 55\end{align*}$ . Now, plug s and the three sides into Heron’s Formula and simplify.
  ::首先,您需要找到 s: s=12( 23+41+46) = 55。 现在, 将 s 和三边插入 Heron 的公式并简化 。

  播放段落

  $$\begin{align*}K & = \sqrt{55(55-23)(55-46)(55-41)} \\ K & = \sqrt{55(32)(9)(14)} \\ k & = \sqrt{221760} \\ K & \approx 470.9\end{align*}$$
  ::K55(55-23)(55-46)(55-41)K55(32)(9)(14)k221760K470.9)

  播放段落

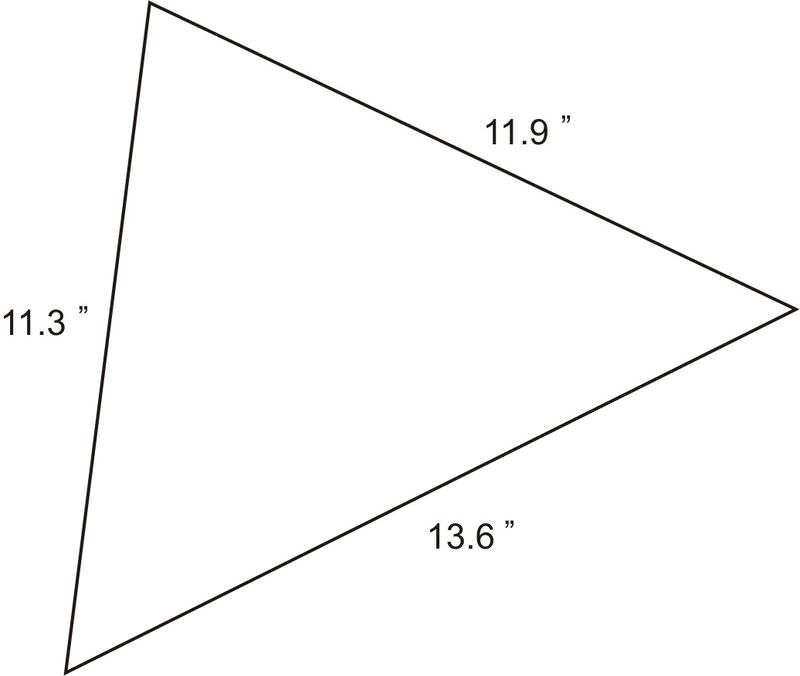
  2. A handyman is installing a tile floor in a kitchen. Since the corners of the kitchen are not exactly square, he needs to have special triangular shaped tile made for the corners. One side of the tile needs to be 11.3”, the second side needs to be 11.9”, and the third side is 13.6”. If the tile costs $\begin{align*}\$4.89\end{align*}$ per square foot, and he needs four of them, how much will it cost to have the tiles made?
  ::2. 一名杂工在厨房安装瓷砖地板,由于厨房的角落不完全平方,他需要为角落制作特殊的三角形瓷砖;瓷砖的一方需要11.3张;第二面需要11.9张;第三面需要13.6张;如果瓷砖每平方英尺需要4.89美元,而他需要4张,那么制作瓷砖要花多少钱?

  

  播放段落

  In order to find the cost of the tiles, we first need to find the area of one tile. Since we know the measurements of all three sides, we can use Heron’s Formula to calculate the area.
  ::为了找到瓷砖的成本,我们首先需要找到一块瓷砖的面积。 由于我们知道所有三边的测量方法,我们可以使用Heron的公式来计算面积。

  播放段落

  $$\begin{align*}s & = \frac{1}{2}(11.3 + 11.9 + 13.6) = 18.4 \\ K & = \sqrt{18.4(18.4 - 11.3)(18.4 - 11.9)(18.4 - 13.6)} \\ K & = \sqrt{18.4(7.1)(6.5)(4.8)} \\ K & = \sqrt{4075.968}\\ K & \approx63.843\ in^2\end{align*}$$
  ::=12(11.3+11.9+13.6)=18.4KQ18.4(18.4-11.3)(18.4-11.3)(18.4-11.9)(18.4-11.9)(18.4-13.6)(K)18.4(7.1)(6.5)(4.8)K4075.968K63.843 in2)

  播放段落

  The area of one tile is 63.843 square inches. The cost of the tile is given to us in square feet, while the area of the tile is in square inches. In order to find the cost of one tile, we must first convert the area of the tile into square feet.
  ::一个瓷砖的面积是63.843平方英寸。瓷砖的成本以平方英尺表示,而瓷砖的面积则以平方英寸表示。为了找到一块瓷砖的成本,我们必须首先将瓷砖的面积转换成平方英尺。

  播放段落

  $$\begin{align*}1\ \text{square foot} & = 12in \times 12in = 144in^2 \\ \frac{63.843}{144} & = 0.443\ ft^2 && \text{Convert square inches into square feet} \\ 0.443\ ft^2 \times 4.89 & = 2.17 && \text{Multiply by the cost of the tile}.\\ 2.17 \times 4 & = 8.68\end{align*}$$
  ::1平方英尺=12inx12in=144in263.843144=0.443平方英寸为平方英尺0.443平方英尺=2.243平方英尺=2.489平方英尺=2.17平方英尺=2.17平方英尺,按平方英尺2.17×4=8.68的成本计算。

  播放段落

  The cost for four tiles would be $\begin{align*}\$8.68\end{align*}$ .
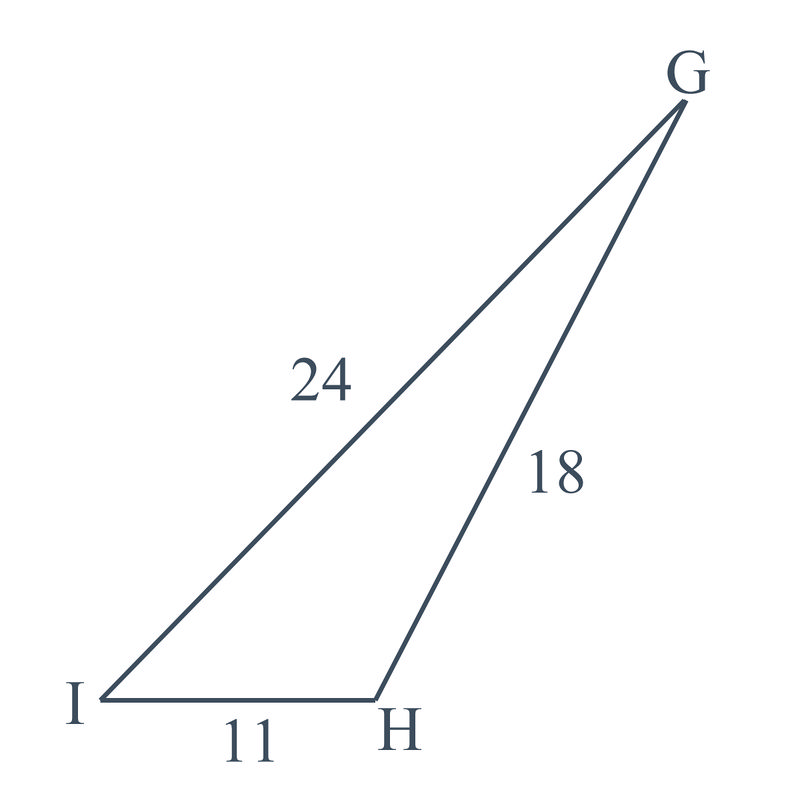
  ::四张瓷砖的费用为8.68美元。

  播放段落

  3. In $\begin{align*}\triangle{GHI}, g = 11, h = 24\end{align*}$ , and $\begin{align*}i = 18\end{align*}$ . Find the area of the triangle.
  ::3. 在 GHI, g=11, h=24, 和i=18。 找到三角形的区域 。

  

  播放段落

  First, you need to find $\begin{align*}s\end{align*}$ : $\begin{align*}s = \frac{1}{2}(11 + 24 + 18) = 26.5\end{align*}$ . Now, plug s and the three sides into Heron’s Formula and simplify.
  ::首先,您需要找到 s: s=12( 11+24+18) =26.5。 现在, 在 Heron 的公式中插入 s 和三边, 并简化 。

  播放段落

  $$\begin{align*}K & = \sqrt{26.5(26.5-11)(26.5-24)(26.5-18)} \\ K & = \sqrt{26.5(15.5)(2.5)(8.5)} \\ k & = \sqrt{8728.44} \\ K & \approx 93.43\end{align*}$$
  ::K26.5(26.5-11)(26.5-24)(26.5-18)(26.5-24)(26.5-18)K}26.5(15.5)(2.5)(8.5)k8728.44K93.43

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a problem about the pyramid. 
  ::之前,你被问及金字塔的问题

  播放段落

  You can use Heron's Formula to find the area of one of the faces of the pyramid.
  ::你可以用Heron的公式 找到金字塔面孔之一的面积

  播放段落

  The equation for the area of the triangle is: $\begin{align*}K = \sqrt{s(s - a)(s - b)(s - c)}\end{align*}$ where $\begin{align*}s =\frac{1}{2}(a+b+c)\end{align*}$ or half of the perimeter of the triangle.
  ::三角形区域的方程是:S=12(a+b+c)或三角形半边角的Ks(s-a)(s-b)(s-c)。

  播放段落

  so, in this case,
  ::所以,在这种情况下,

  播放段落

  $\begin{align*}s =\frac{1}{2}(200+175+175) = \frac{550}{2} = 225\end{align*}$
  ::=12(200+175+175)=5502=225

  播放段落

  And
  ::还有

  播放段落

  $\begin{align*}K = \sqrt{225(225-200)(225-175)(225-175)} = 3,750\end{align*}$ square meters.
  ::K225(225-200)(225-175)(225-175)=3,750平方米。

  播放段落

  Example 2
  ::例2

  播放段落

  Use Heron's formula to find the area of a triangle with the following sides: $\begin{align*}HC = 4.1, CE = 7.4\end{align*}$ , and $\begin{align*}HE = 9.6\end{align*}$
  ::使用 Heron 的公式来找到三角形区域,其侧面如下: HC=4.1, CE=7.4, HE=9.6。

  

  播放段落

  $\begin{align*}A = 14.3\end{align*}$
  ::A=14.3 A=14.3

  播放段落

  Example 3
  ::例3

  播放段落

  The Pyramid Hotel is planning on repainting the exterior of the building. The building has four sides that are isosceles triangles with bases measuring 590 ft and legs measuring 375 ft.
  ::金字塔酒店正计划对大楼外部进行再油漆,大楼有四面是等分三角形,基地590英尺,腿375英尺。

  播放段落

  What is the total area that needs to be painted?
  ::需要绘制的总面积是多少?

  播放段落

  Use Heron’s Formula, then multiply your answer by 4, for the 4 sides.
  ::使用 Heron 的公式, 然后将您的答复乘以 4 乘以 4 。

  播放段落

  $\begin{align*}s = \frac{1}{2}(375 + 375 + 590) = 670\end{align*}$
  ::=12(375+375+590)=670

  播放段落

  $\begin{align*}A = \sqrt{670(670 - 375)(670-375)(670-590)} = 68,297.4\end{align*}$
  ::A670(670-375)(670-375)(670-590)=68 297.4

  播放段落

  The area multiplied by 4: $\begin{align*}68,297.4\cdot 4 = 273,189.8\end{align*}$ total square feet.
  ::面积乘以4:68 297.4 4= 273 189.8总平方英尺。

  播放段落

  If one gallon of paint covers 25 square feet, how many gallons of paint are needed?
  ::如果一加仑的油漆覆盖25平方英尺,需要多少加仑的油漆?

  播放段落

  $\begin{align*}\frac{273,189.8}{25} \approx 10,928\end{align*}$ gallons of paint are needed.
  ::需要273,189.82510,928加仑油漆。

  播放段落

  Example 4
  ::例4

  播放段落

  A contractor needs to replace a triangular section of roof on the front of a house. The sides of the triangle are 8.2 feet, 14.6 feet, and 16.3 feet. If one bundle of shingles covers $\begin{align*}33 \ \frac{1}{3}\end{align*}$ square feet and costs $\begin{align*}\$15.45\end{align*}$ , how many bundles does he need to purchase? How much will the shingles cost him? How much of the bundle will go to waste?
  ::承包商需要更换房子前面的三边屋顶。 三角形的两边是8. 2英尺、 14. 6英尺和 16. 3英尺。 如果一捆闪光覆盖33 13平方英尺, 费用为15. 45美元, 他需要购买多少捆? 闪光要花多少钱? 捆闪光会浪费多少?

  播放段落

  Using Heron’s Formula, s and the area are: $\begin{align*}s = \frac{1}{2}(8.2 + 14.6+16.3) = 19.55\end{align*}$ and $\begin{align*}A = \sqrt{19.55(19.55 - 8.2)(19.55-14.6)(19.55 - 16.3)} = 59.75\ sq. ft.\end{align*}$ He will need 2 bundles $\begin{align*}\left (\frac{59.75}{33.3} = 1.8 \right )\end{align*}$ . The shingles will cost him $\begin{align*}2\cdot \$15.45 = \$30.90\end{align*}$ and 6.92 square feet will go to waste $\begin{align*}(66.67-59.75 = 6.92)\end{align*}$ .
  ::使用Heron的公式,S和面积是:s=12(8.2+14.6+16.3)=19.55和A19.55(19.55-8.2)(19.55-14.6)(19.55-16.3)=59.75 sq.ft。他需要2捆(59.7533.3=1.8)。 闪光将花费他2+15.45美元=30.90美元,6.92平方英尺将浪费(66.67-59.75=6.92)。

  播放段落

  Review
  ::回顾

  播放段落

  Find the area of each triangle with the three given side lengths.
  ::以给定的三边长度查找每个三角形的区域 。

  1. 2, 14, 15
  2. 6, 8, 9
  3. 10, 14, 20
  4. 11, 15, 6
  5. 4, 4, 4
  6. 4, 5, 3
  7. 32, 40, 50
  8. 20, 18, 22
  9. 20, 20, 20
  10. 18, 17, 12
  11. 9, 12, 10
  12. 11, 18, 8
  播放段落
  13. Describe when it makes the most sense to use Heron's formula to find the area of a triangle.
      ::使用 Heron 的公式查找三角形区域最合情合理时, 请描述 。
  播放段落
  14. A tiling is made of 30 congruent triangles. The lengths of the sides of each triangle are 3 inches, 5 inches, and 7 inches. What is the area of the tiling?
      ::砖块由 30 个相似的三角形组成。 三角形两边的长度是 3 英寸、 5 英寸和 7 英寸。 砖块的面积是 多少 ?
  播放段落
  15. What type of triangle with have the maximum area for a given perimeter? Show or explain your reasoning.
      ::哪种三角形具有给定周边的最大面积? 显示或解释您的理由 。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。