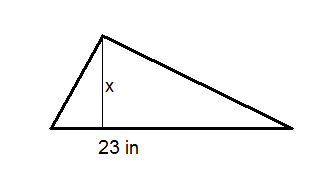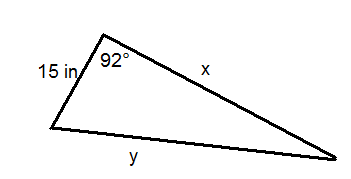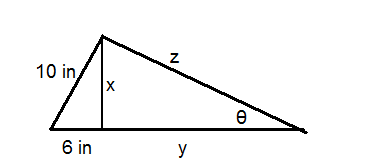5.6 确定未知三角区特定面积措施

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 确定未知三角区特定面积措施

  Collapse Expand

  确定未知三角区特定面积措施

  播放段落

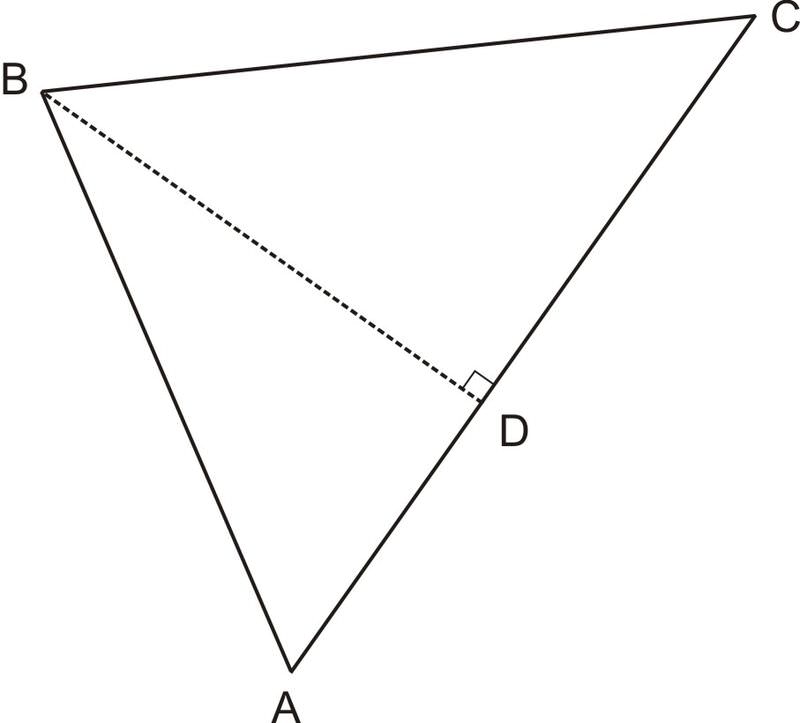
  You are working on creating a mobile for your art class. A mobile is a piece of art that has a rod with different shapes hanging from it, so they can spin.
  ::您正在为您的艺术类创建手机。 手机是一种艺术作品, 上面挂着不同形状的棒子, 这样它们可以旋转。

  播放段落

  To create your project, you need to cut a set of triangles that have a variety of sizes. You are about to start cutting triangles, when your friend, who is helping you with the project, comes over. She tells you that each piece needs to have a rod through the side of it to balance the shape in a certain way. She wants you to make a piece that looks like this:
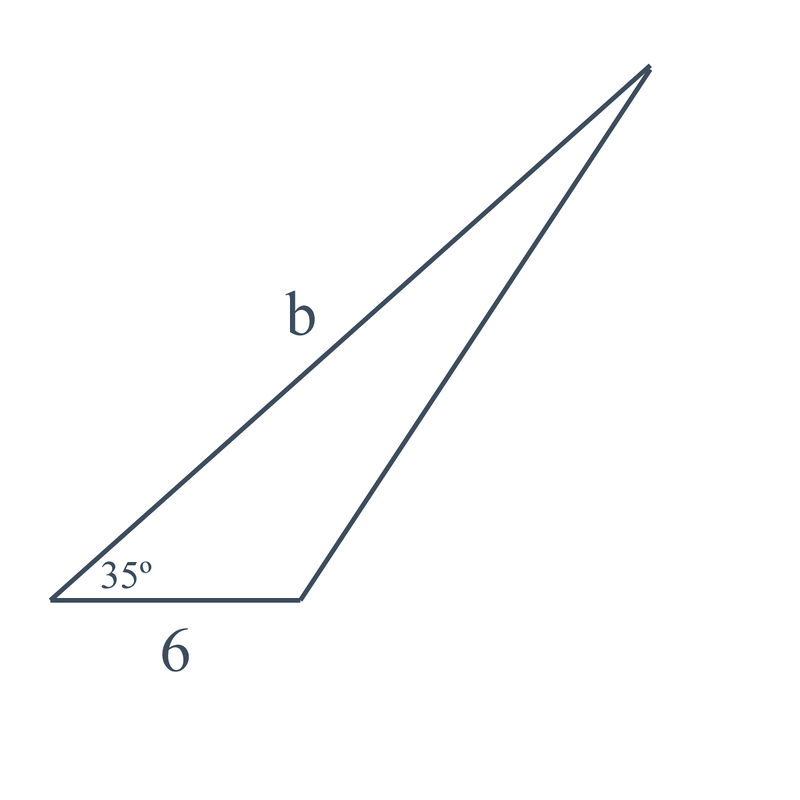
  ::要创建您的工程, 您需要切开一组三角形, 三角形大小各异。 您即将开始切开三角形, 当帮助您执行此工程的朋友过来时, 她告诉你每块需要一根棍子通过它的侧面, 才能以某种方式平衡形状 。 她希望您制作一块像这样的三角形 :

  

  播放段落

  You have already cut a triangle by cutting a piece out of construction paper. You know that one side of your triangle is 6 inches long, but you don't know the length of the other two sides. Can you use the information you have to find the length of $\begin{array}{r}b\end{array}$ in the mobile piece above? (The area of the triangle is $\begin{array}{r}25i{n}^2\end{array}$ , and the interior angle between the six inch side and the side you want to know is $\begin{array}{r}{35}^{\circ }\end{array}$ ).
  ::您已经通过剪切建筑纸的一块块剪切了三角形。 您知道三角形的一边长6英寸, 但是您不知道另外两边的长度 。 您能否使用您需要的信息在以上移动片段找到 b 的长度 ? (三角形区域是 25 英寸 2 , 6 英寸侧与您想知道的侧之间的内角是 35 英寸 ) 。

  播放段落

  Finding the Measures of a Triangle Given the Area
  ::" 区域 " 内三角区的措施

  播放段落

  In this section, we will look at situations where we know the area but need to find another part of the triangle, as well as an application involving a quadrilateral. All of this will involve the use of the , , and the Alternate Formula for the Area of a Triangle.
  ::在本节中,我们将审视我们了解区域但需要找到三角区另一部分的情况,以及涉及四边形的申请。 所有这些都涉及使用 、 和三角区替代公式。

  播放段落

  1. The jib sail on a sailboat came untied and the rope securing it was lost. If the area of the jib sail is 56.1 square feet, use the figure and information below to find the length of the rope.
  ::1. 帆船上的船帆松开,安全绳索丢失,如果船帆面积为56.1平方英尺,用下面的数字和资料找到绳索的长度。

  

  播放段落

  Since we know the area, one of the sides, and one angle of the jib sail, we can use the formula $\begin{array}{r}K=\frac{1}{2}bc\sin A\end{array}$ to find the side of the jib sail that is attached to the mast. We will call this side $\begin{array}{r}y\end{array}$ .
  ::既然我们知道这个区域,一个侧面,一个方向, 和jib帆的一个角度, 我们可以使用公式 K=12 bcsinA 来找到连接在顶杆上的 jib帆的侧面。我们称它为Y。

  播放段落

  %5Csin%2011%20%5C%5C%0A56.1%20%26%20%3D%202.671325935%5C%20y%20%5C%5C%0A21.0%20%26%20%3D%20y">

  $$\begin{array}{rl}56.1& =\frac{1}{2}28(y)\sin 11\\ 56.1& =2.671325935y\\ 21.0& =y\end{array}$$

  
  ::56.1=12 28sin1156.1=2.671325935y21.0=y

  播放段落

  Now that we know side $\begin{array}{r}y\end{array}$ , we know two sides and the included angle in the triangle formed by the mast, the rope, and the jib sail. We can now use the Law of Cosines to calculate the length of the rope.
  ::现在我们知道侧面了。 我们知道了两面和三角形中包括的角度,三角形是由船顶、绳子和帆组成的。我们现在可以使用科辛斯定律来计算绳子的长度。

  播放段落

  $$\begin{array}{rl}{x}^2& ={21}^2+{27}^2-2(21)(27)\cos 18\\ x^2& =91.50191052\\ x& \approx 9.6ft\end{array}$$

  
  ::x2=212+272-2(21)(27cos18x2=91.50191052x9.6英尺)

  播放段落

  The length of the rope is approximately 9.6 feet.
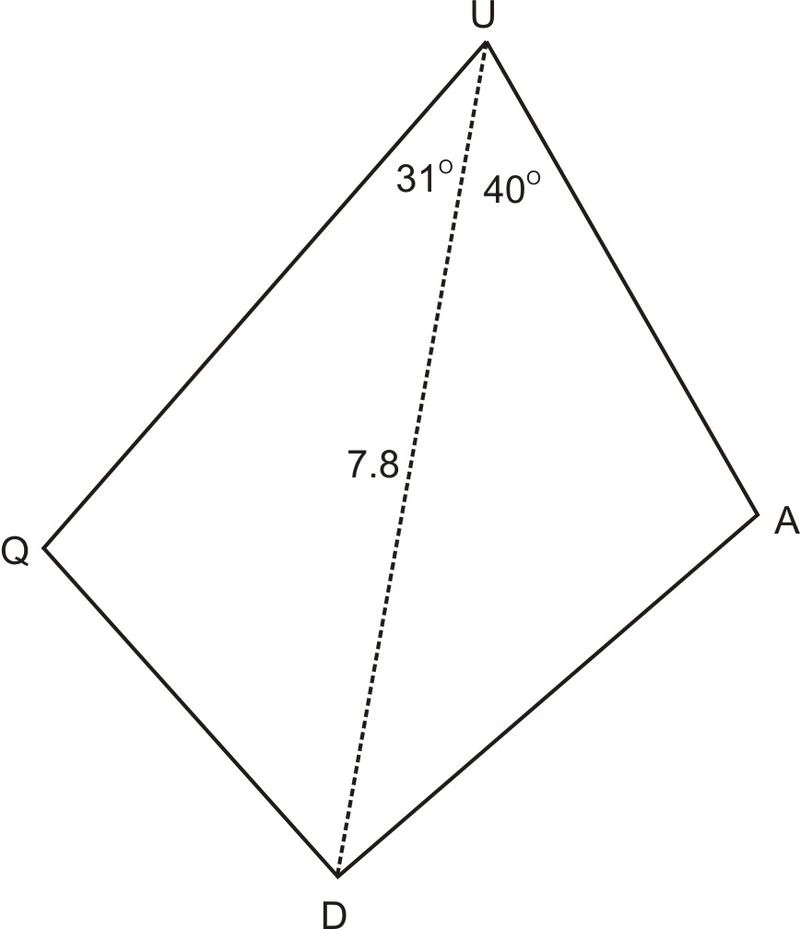
  ::绳索的长度约为9.6英尺。

  播放段落

  2. In quadrilateral $\begin{array}{r}QUAD\end{array}$ below, the area of $\begin{array}{r}\mathrm{△}QUD=5.64\end{array}$ , the area of $\begin{array}{r}\mathrm{△}UAD=6.39,\mathrm{\angle }QUD={31}^{\circ },\mathrm{\angle }DUA={40}^{\circ }\end{array}$ , and $\begin{array}{r}UD=7.8\end{array}$ . Find the perimeter of $\begin{array}{r}QUAD\end{array}$ .
  ::2. 在以下四边QUAD中,ZUD=5.64的区域,ZUAD=6.39,ZUAD=31,ZUDA=40,UD=7.8。 找出QUAD的周界。

  

  播放段落

  In order to find the perimeter of $\begin{array}{r}QUAD\end{array}$ , we need to know sides $\begin{array}{r}QU,QD,UA\end{array}$ , and $\begin{array}{r}AD\end{array}$ . Since we know the area, one side, and one angle in each of the triangles, we can use $\begin{array}{r}K=\frac{1}{2}bc\sin A\end{array}$ to figure out $\begin{array}{r}QU\end{array}$ and $\begin{array}{r}UA\end{array}$ .
  ::为了找到QUAD的周边,我们需要知道QU、QD、UA和AD的侧面。因为我们知道每个三角形的面积、一面和角,我们可以用K=12 bcsinA来找出QU和UA。

  播放段落

  $$\begin{array}{rlrl}5.64& =\frac{1}{2}(7.8)(QU)\sin 31& & 6.39=\frac{1}{2}(7.8)UA\sin 40\\ 2.8& \approx QU& & 2.5\approx UA\end{array}$$

  
  ::5.64=12(7.8)(QU)sin316.39=12(7.8)UAsin402.8U2.5UA

  播放段落

  Now that we know $\begin{array}{r}QU\end{array}$ and $\begin{array}{r}UA\end{array}$ , we know two sides and the included angle in each triangle (SAS). This means that we can use the Law of Cosines to find the other two sides, $\begin{array}{r}QD\end{array}$ and $\begin{array}{r}DA\end{array}$ . First we will find $\begin{array}{r}QD\end{array}$ and $\begin{array}{r}DA\end{array}$ .
  ::现在我们知道QU和UA了, 我们知道了两个侧面, 每个三角形(SAS)中包含的角度。 这意味着我们可以使用Cosines定律找到另外两个侧面, QD和DA。 首先我们会找到QD和DA。

  播放段落

  $$\begin{array}{rlrl}Q{D}^2& ={2.8}^2+{7.8}^2-2(2.8)(7.8)\cos 31& & D{A}^2={2.5}^2+{7.8}^2-2(2.5)(7.8)\cos 40\\ Q{D}^2& =31.23893231& & D{A}^2=37.21426672\\ QD& \approx 5.6& & DA\approx 6.1\end{array}$$

  
  ::QD2 = 2.82+7.82-2(2.8)(7.8)cos 31DA2 = 2.52+7.82-2(2.5)(7.8)cos QD2 = 31.23893231DA2 = 37.21426672QD 5.6DA_6.1

  播放段落

  Finally, we can calculate the perimeter since we have found all four sides of the quadrilateral.
  ::最后,我们可以计算周界,因为我们找到了四边线的所有四面线。

  播放段落

  $$\begin{array}{r}pQUAD=2.8+5.6+6.1+2.5=17\end{array}$$

  
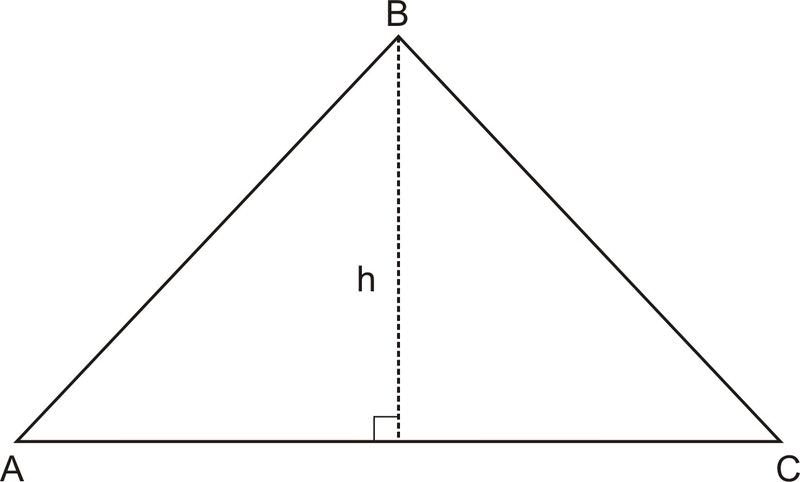
  ::pUAD=2.8+5.6+6.1+2.5=17

  播放段落

  3. In $\begin{array}{r}\mathrm{△}ABC,BD\end{array}$ is an altitude from $\begin{array}{r}B\end{array}$ to $\begin{array}{r}AC\end{array}$ . The area of $\begin{array}{r}\mathrm{△}ABC=232.96,AB=16.2\end{array}$ , and $\begin{array}{r}AD=14.4\end{array}$ . Find $\begin{array}{r}DC\end{array}$ .
  ::3. 在ABC中,BD是从B到AC的高度。 ABC=232.96、AB=16.2和AD=14.4的区域。

  播放段落

  First, find $\begin{array}{r}BD\end{array}$ by using the . $\begin{array}{r}BD=\sqrt{{16.2}^2-{14.4}^2}=7.42\end{array}$ . Then, using the area and formula $\begin{array}{r}(A=\frac{1}{2}bh)\end{array}$ , you can find $\begin{array}{r}AC\end{array}$ . $\begin{array}{r}232.96=\frac{1}{2}(7.42)AC\to AC=62.78\end{array}$ . $\begin{array}{r}DC=62.78-14.4=48.38\end{array}$ .
  ::首先,使用.BD=16.22-14.42=7.42,找到BD。然后,使用区域和公式(A=12bh),可以找到AC232.96=12(7.42)AC=62.78.DC=62.78-14.4=48.38。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find the length of  $\begin{array}{r}b\end{array}$  in the mobile piece. 
  ::早些时候,你被要求在移动片中找到b的长度。

  播放段落

  Since you know that the mobile piece is six inches on one side, and that the area of the triangle is $\begin{array}{r}25i{n}^2\end{array}$ , you can use the formula $\begin{array}{r}K=\frac{1}{2}ab\sin C\end{array}$ to find the length of the other side:
  ::既然您知道移动片在一边是6英寸, 而三角形的面积是25英寸2, 您可以使用公式 K=12absinC 来找到另一边的长度 :

  播放段落

  $$\begin{array}{r}K=\frac{1}{2}ab\sin C\\ 25=\frac{1}{2}(6)(b)\sin {35}^{\circ }\\ 25=1.72b\\ b=\frac{25}{1.72}\\ b=14.53in\end{array}$$

  
  ::K=12absinC25=12(6)(b)sin3525=1.72bb=251.72b=14.53in

  播放段落

  Example 2
  ::例2

  播放段落

  Find "h" in the triangle below: Area $\begin{array}{r}=1618.98,b=36.3\end{array}$
  ::在以下三角形中查找“h”:面积=1618.98,b=36.3

  

  播放段落

  Since we know the area, one of the sides (18.15), and one angle of the triangle ( $\begin{array}{r}{45}^{\circ }\end{array}$ ), we can use the formula $\begin{array}{r}K=\frac{1}{2}bc\sin A\end{array}$ to find the other side of the triangle. We can then use the Pythagorean Theorem to find the height of the triangle.
  ::既然我们知道区域, 边边之一( 18.15) , 三角形的一个角度( 45) , 我们可以使用公式 K= 12 bcsinA 来找到三角形的另一边。 然后我们可以使用 Pytagoren 理论来找到三角形的高度 。

  播放段落

  This gives a result of:
  ::其结果是:

  播放段落

  $\begin{array}{r}h=89.2\end{array}$
  ::h=89.2

  播放段落

  Example 3
  ::例3

  播放段落

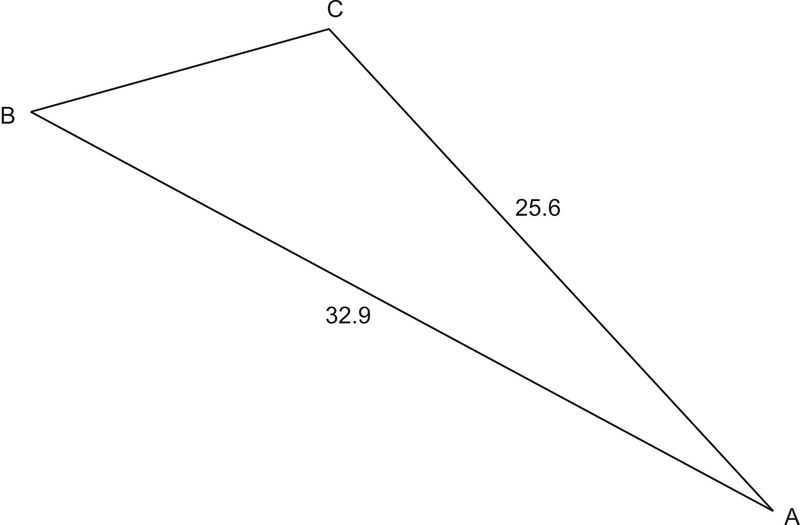
  Find $\begin{array}{r}\mathrm{\angle }A\end{array}$ in the triangle below: Area $\begin{array}{r}=387.6,b=25.6,c=32.9\end{array}$
  ::在以下三角形中查找A:面积=387.6,b=25.6,c=32.9。

  

  播放段落

  Since we know the area and the lengths of two of the sides of the triangle, we can use the formula $\begin{array}{r}K=\frac{1}{2}bc\sin A\end{array}$ to solve for the included angle, which gives:
  ::由于我们知道三角形两边的面积和长度,我们可以使用公式K=12 bcsinA来解决包含的角度,它提供:

  播放段落

  $\begin{array}{r}\mathrm{\angle }A={67}^{\circ }\end{array}$
  ::A=67

  播放段落

  Example 4
  ::例4

  播放段落

  Find the area of $\begin{array}{r}\mathrm{△}ABC\end{array}$ below: Area $\begin{array}{r}\mathrm{△}ABD=16.96,AD=3.2,\mathrm{\angle }DBC={49.6}^{\circ }\end{array}$
  ::在以下区域查找ABC区域:are area ABD=16.96,AD=3.2,DBC=49.6

  

  播放段落

   Area of $\begin{array}{r}\mathrm{△}ABC=83.0\end{array}$
  ::ABC=83.0的面积

  播放段落

  Review
  ::回顾

  播放段落
  1. The area of the triangle below is $\begin{array}{r}138i{n}^2\end{array}$ . Solve for x, the height.
     ::下面三角形的面积是138in2。 解决 x, 高度 。
  播放段落
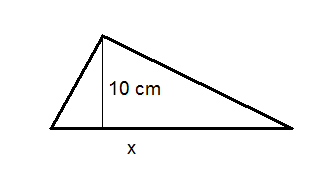
  2. The area of the triangle below is $\begin{array}{r}250c{m}^2\end{array}$ . A height is given on the diagram. Solve for x.
     ::下面三角形的面积是250厘米2。图中给出了高度。为 x 解密 。

  播放段落

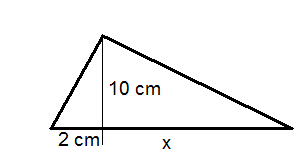
  Use the triangle below for questions 3-5. The area of the large triangle is $\begin{array}{r}65c{m}^2\end{array}$ .
  ::问题3-5使用下面的三角形。大三角形的面积为65cm2。

  

  播放段落
  3. Solve for x.
     ::解决x。
  播放段落
  4. Find the perimeter of the large triangle.
     ::找到大三角形的周边
  播放段落
  5. Find the measure of all three angles of the large triangle.
     ::查找大三角形所有三个角度的度量。

  播放段落

  Use the triangle below for questions 6-8. The area of the triangle is $\begin{array}{r}244c{m}^2\end{array}$ .
  ::问题 6-8 使用下面的三角形。 三角形区域为 244 cm2。

  

  播放段落
  6. Solve for $\begin{array}{r}\theta \end{array}$ .
     ::解决... . .
  播放段落
  7. Solve for x.
     ::解决x。
  播放段落
  8. Find the perimeter of the triangle.
     ::找到三角形的周边

  播放段落

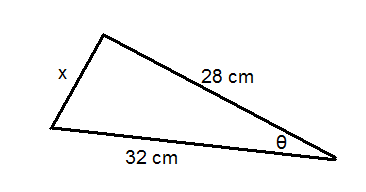
  Use the triangle below for questions 9-11. The area of the triangle is $\begin{array}{r}299.8i{n}^2\end{array}$ .
  ::问题9-11使用下面的三角形。三角形的面积为299.8英寸2。

  

  播放段落
  9. Solve for x.
     ::解决x。
  播放段落
  10. Solve for y.
      ::解决你。
  播放段落
  11. Find the measure of the other two angles of the triangle.
      ::查找三角形其他两个角度的度量。

  播放段落

  Use the triangle below for questions 12-15. The area of the large triangle is $\begin{array}{r}84i{n}^2\end{array}$ .
  ::问题12-15使用下面的三角形。大三角形的面积为84英寸2。

  

  播放段落
  12. Solve for x.
      ::解决x。
  播放段落
  13. Solve for y.
      ::解决你。
  播放段落
  14. Solve for z.
      ::解决z。
  播放段落
  15. Solve for $\begin{array}{r}\theta \end{array}$ .
      ::解决... . .

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。