2.1 找出线的斜度和平方
章节大纲
-
The grade, or , of a road is measured in a percentage. For example, if a road has a downgrade of 7%, this means, that over every 100 horizontal feet, the road will slope down 7 feet vertically .
::道路的等级或程度以百分比衡量。 比如,如果道路降级为7%,这意味着每100个水平英尺,公路将垂直向下倾斜7英尺。If a highway has a downgrade of 12% for 3 miles (5280 feet in a mile), how much will the road drop? What is the slope of this stretch of highway?
::如果一条高速公路在3英里(每英里5280英尺)上降12%,公路会跌落多少?这段公路的斜坡是多少?Finding the Slope and Equation of a Line
::查找线条的曲率和公式The slope of a line determines how steep or flat it is. When we place a line in the coordinate plane , we can measure the slope, or steepness, of a line. Recall the parts of the coordinate plane, also called a plane and the Cartesian plane , after the mathematician Descartes.
::线的斜坡决定它有多陡峭或平坦。 当我们在坐标平面上设置一条线时, 我们可以测量线的斜度或陡度。 回顾坐标平面的各个部分, 也称为X- y 平面和笛卡尔平面, 以数学运货师为后。To plot a point, order matters. First, every point is written where is the movement in the direction and is the movement in the direction. If is negative, the point will be in the or quadrants . If is negative, the point will be in the or quadrants. The quadrants are always labeled in a counter-clockwise direction and using Roman numerals.
::要绘制一个点, 命令很重要 。 首先, 每个点都是书面的 (x, y) , 其中 x 是 x - 方向的移动, y 是 y - 方向的移动 。 如果 x 是负的, 点将是 2 或 3 之四 。 如果 y 是 负的, 点将是 3 或 4 之四 。 四重点总是以反时针方向贴上标签, 并使用罗马数字 。The point in the quadrant would be (9, -5).
::第四象限的点将是( 9, 5 ) 。To find the slope of a line or between two points, first, we start with right triangles. Let’s take the two points (9, 6) and (3, 4). Plotting them on a plane, we have:
::为了找到一条线的斜坡或两点之间的斜坡, 首先, 我们从右三角开始。 让我们选择两点( 9, 6 ) 和 ( 3, 4 ) 。 在 x - y 平面上绘制它们, 我们有 :To turn this segment into a right triangle, draw a vertical line down from the higher point, and a horizontal line from the lower point, towards the vertical line. Where the two lines intersect is the third vertex of the slope triangle.
::要将此段转换为右三角形, 请从高点向下绘制一条垂直线, 从下点向下绘制一条水平线, 到垂直线。 在两条线相交之处, 两条线是斜度三角形的第三个顶点 。Now, count the vertical and horizontal units along the horizontal and vertical sides ( dotted lines).
::现在,沿着水平和垂直两侧(红色虚线)计算垂直和水平单位。The slope is a fraction with the vertical distance over the horizontal distance, also called the “ rise over run .” Because the vertical distance goes down, we say that it is -2. The horizontal distance moves towards the negative direction (the left), so we would say that it is -6. So, for slope between these two points, the slope would be or .
::斜坡是水平距离垂直距离的一个小块,水平距离上也称为“环向上升 ” 。 因为垂直距离是 -2. 水平距离向负方向(左)移动,所以我们说它就是 -6. 因此,对于这两点之间的斜坡来说,斜坡将是-2-6或13。Note : You can also draw the right triangle above the line segment.
::注意:您也可以在线段上绘制右三角形。Now, let's find the slope of the following lines.
::现在,让我们找到以下线条的斜坡。-
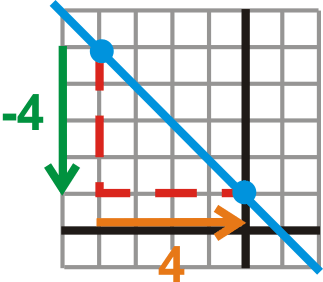
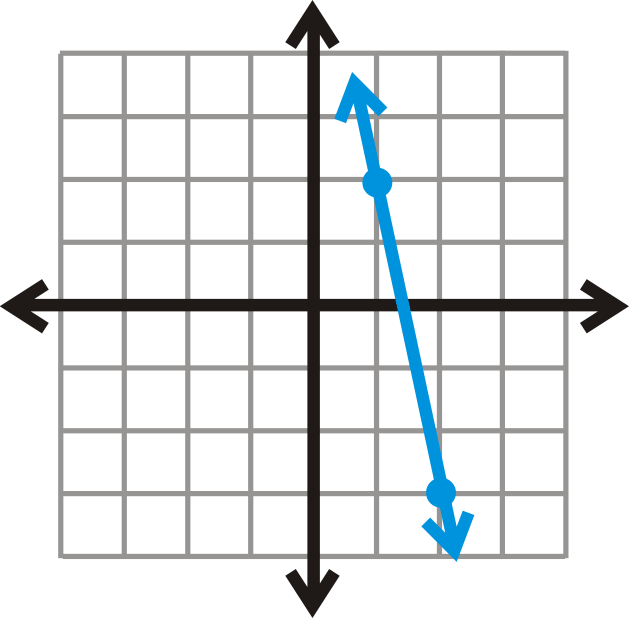
Use a slope triangle to find the slope of the line below.
::使用斜度三角形查找下线的斜度。
Notice the two points that are drawn on the line. These are given to help you find the slope. Draw a triangle between these points and find the slope.
::注意线上绘制的两点。 这些是用来帮助您找到斜坡的。 在这些点之间绘制三角形并找到斜坡 。From the slope triangle above, we see that the slope is .
::从上面的斜坡三角形,我们看到斜坡是 - 441。Whenever a slope reduces to a whole number, the “run” will always be positive 1. Also, notice that this line points in the opposite direction as the line segment above. We say this line has a negative slope because the slope is a negative number and points from the to quadrants. A line with positive slope will point in the opposite direction and point between the and quadrants.
::1. 另外,请注意,这条线点与上面的线段方向相反。我们说,这条线的斜坡是负的,因为斜坡是2号至4号方位的负数和点。正斜坡的直线将指向1号和3号方位之间的相反方向和点。-
If we go back to our previous example with points (9, 6) and (3, 4), we can find the vertical distance and horizontal distance another way.
::如果我们回到我们以前的例子,加上点(9,6)和点(3,4),我们可以找到另一条垂直距离和水平距离。
From the picture, we see that the vertical distance is the same as the difference between the values and the horizontal distance is the difference between the values. Therefore , the slope is . We can extend this idea to any two points, and .
::从图中可以看出,垂直距离与 y- 值和水平距离之间的差别是相同的。 因此,斜坡是 6-49-3 。 我们可以将这个概念扩大到任何两个点, (x1,y1) 和 (x2,y2) 。Slope Formula : For two points and the slope between them is . The symbol for slope is .
::斜坡公式: 对于两个点(x1,y1)和(x2,y2),两点之间的斜坡是 y2-y1,x2-x1. 斜坡的符号是 m。It does not matter which point you choose as or .
::您选择哪个点为 (x1,y1) 或 (x2,y2) 并不重要 。Let's find the slope of the following lines using the Slope Formula.
::让我们用“斜坡公式”找到以下线条的斜坡。-
Find the slope between (-4, 1) and (6, -5).
::在(4、1)和(6、5)之间找到斜坡。
Set and .
::设置 (x1,y1) = (- 4, 1) 和 (x2,y2) = (6, 5) 。
::my2-y1x2-x1=6-(-4)-5-1=10-653-
Find the slope between (9, -1) and (2, -1).
::查找在(9,-1)和(2,-1)之间的斜坡。
Set and .
::设置 (x1,y1) =(9,-1) 和(x2,y2) =(2,-1)。
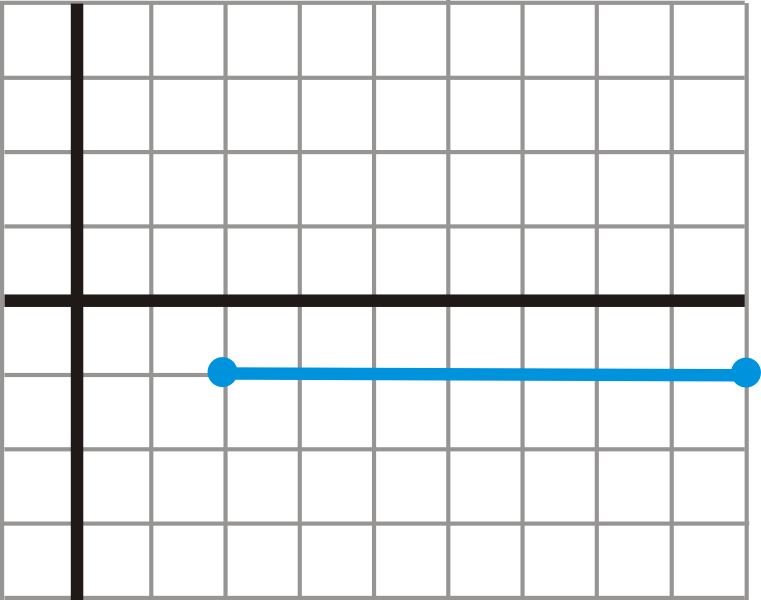
::m1-(- 1)2-9=0-7=0Here, we have zero slope . Plotting these two points we have a horizontal line. This is because the values are the same. Anytime the values are the same we will have a horizontal line and the slope will be zero.
::在这里,我们有零斜度。 绘制这两个点的横线。 这是因为 y - 值是相同的。 只要 y - 值是相同的, 我们就会有一个水平线, 而斜度是零 。Examples
::实例Example 1
::例1Earlier, you were asked to find how much the road will drop and the slope of the stretch of highway.
::早些时候,有人要求你找到 道路将下降多少 和高速公路的斜坡。The road slopes down 12 feet over every 100 feet.
::路坡每100英尺下下12英尺。Let's set up a ratio to find out how much the road slopes in 3 miles, or feet.
::让我们设定一个比率 来找出三英里内 公路坡有多高 也就是3 5 5 280=15 840英尺
::12100=x15,8401584012100=xx=1900.8The road drops 1900.8 feet over the 3 miles. The slope of the road is or when the fraction is reduced.
::公路在3英里处跌落1900.8英尺,路坡为12100或325英尺,当分数减少时。Example 2
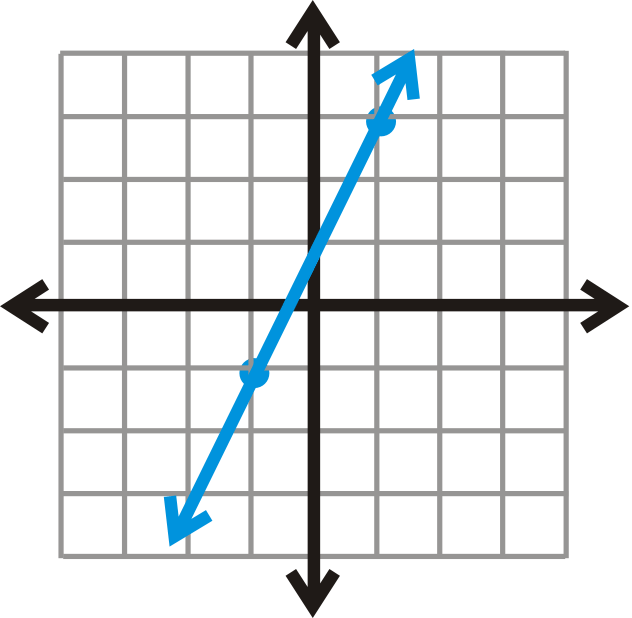
::例2Use a slope triangle to find the slope of the line below.
::使用斜度三角形查找下线的斜度。Counting the squares, the vertical distance is down 6, or -6, and the horizontal distance is to the right 8, or +8. The slope is then or .
::计算方形时,垂直距离向下为6或-6,水平距离向右为8或+8。 斜度为-68或-23。Example 3
::例3Find the slope between (2, 7) and (-3, -3).
::查找(2、7)和(3、3和3)之间的斜坡。Use the Slope Formula. Set and .
::使用斜坡公式。 设置 (x1,y1) = (2, 7) 和 (x2,y2) = (- 3, 3) 。
::my2 - y1x2 - x1 - x1 - 3 - 7 - 3 - 2 - 2 - 10 - 5=2Example 4
::例4Find the slope between (-4, 5) and (-4, -1).
::在(4、5)和(4、1)之间找到斜坡。Again, use the Slope Formula. Set and .
::再次使用斜坡公式。 设定 (x1, y1) = (- 4, 5) 和 (x2, y2) = (- 4, -1) 。
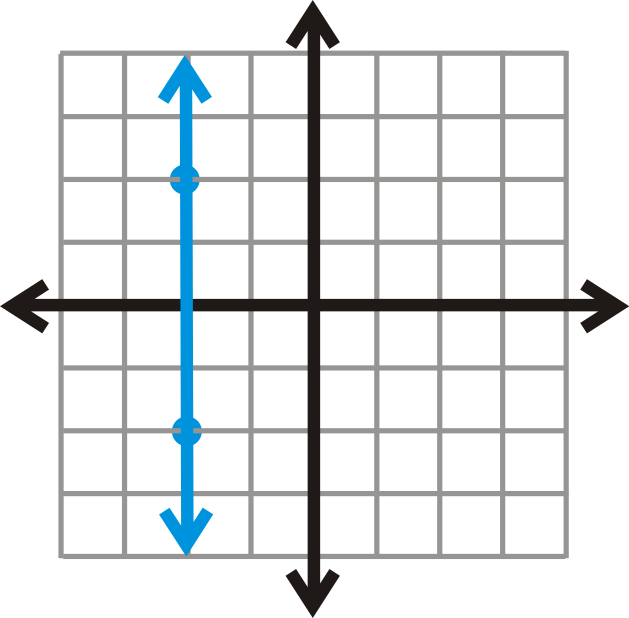
::my2-y1x2-x1_x1___1-5-4-(-4)_(-4)_________________________________________________________________________________________________________________You cannot divide by zero. Therefore, this slope is undefined . If you were to plot these points, you would find they form a vertical line. All vertical lines have an undefined slope .
::您不能除以 0 。 因此, 此斜坡是未定义的 。 如果您要绘制这些点, 您就会发现它们形成一条垂直线 。 所有垂直线都有一个未定义的斜坡 。Important Note : Always reduce your slope fractions. Also, if the numerator or denominator of a slope is negative, then the slope is negative. If they are both negative, then we have a negative number divided by a negative number, which is positive, thus a positive slope.
::重要注意 : 总是减少您的斜坡分数。 另外, 如果斜坡的分子或分母为负数, 那么斜坡为负数。 如果两者均为负数, 那么我们就会发现负数除以负数, 负数是正数, 因此是正数 。Review
::回顾Find the slope of each line by using slope triangles.
::使用斜度三角形查找每条线的斜度。Find the slope between each pair of points using the Slope Formula.
::使用“斜坡公式”在每对点之间查找斜度。-
(-5, 6) and (-3, 0)
:5-5,6)和(3,0)
-
(1, -1) and (6, -1)
:1,-1)和(6,-1)
-
(3, 2) and (-9, -2)
:3,2和3,3,2)和(9,9,2)
-
(8, -4) and (8, 1)
:8,4和8,1)
-
(10, 2) and (4, 3)
:10、2和4、3)
-
(-3, -7) and (-6, -3)
:3-3,7)和(6,6,3)
-
(4, -5) and (0, -13)
:4、5和5)和(0、13)
-
(4, -15) and (-6, -11)
:4,15,4,4,15)和(6,11)
-
(12, 7) and (10, -1)
:12,7)和(10,-1)
-
Challenge
The slope between two points
and (1, -2) is
. Find
and
.
::两点(a、b)和1点(1、2点)之间的斜坡是12点。
Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -
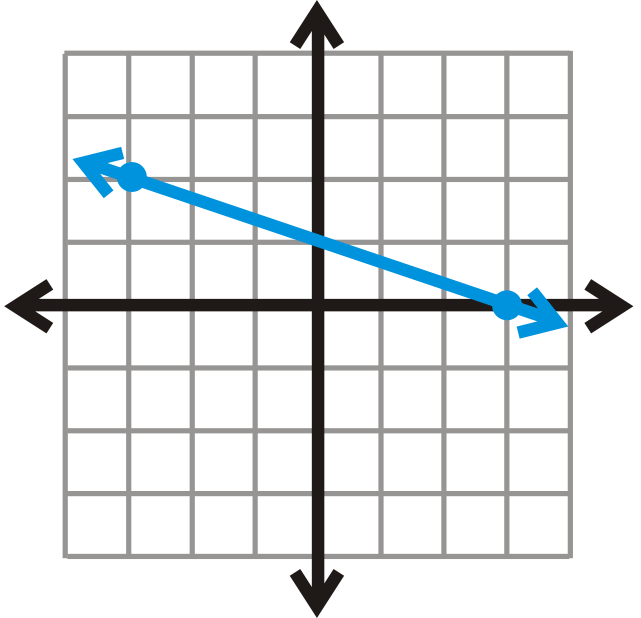
Use a slope triangle to find the slope of the line below.