5.7 角度- 角度- 侧边三角
章节大纲
-
You and a friend decide to go fly kites on a breezy Saturday afternoon. While sitting down to make your kites, you are working on make the best shape possible to catch the breeze. While your friend decides to go with a diamond shaped kite, you try out making a triangle shaped one. While trying to glue the kite together, you make the first and second piece lock together with a angle. The angle between the first and third pieces is . Finally, you also have measured the length of the second piece and found that it is 22 inches long.
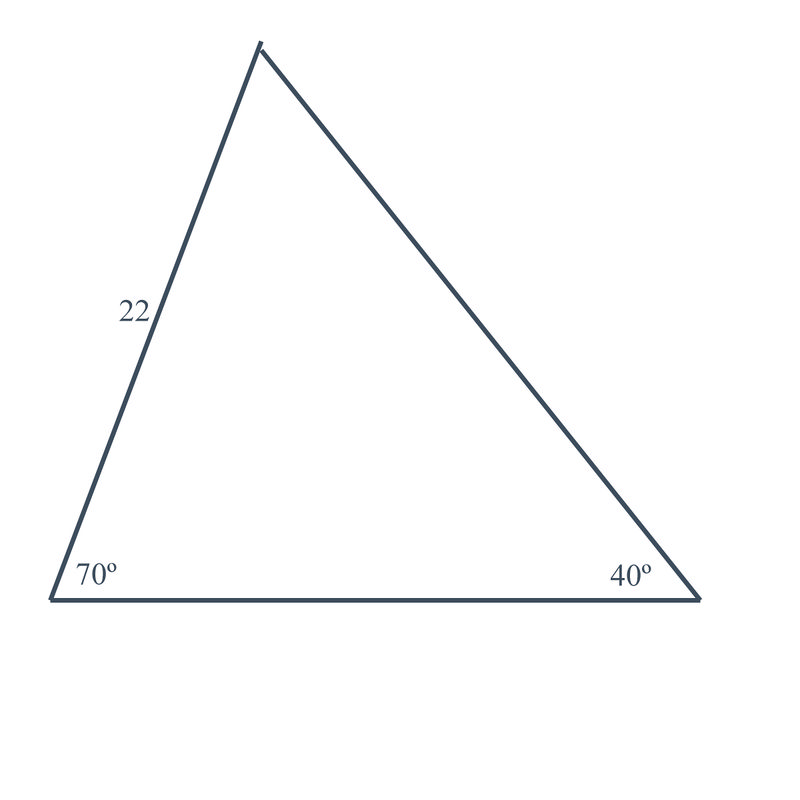
::你和一个朋友决定周六下午去吹风。 当坐下来做风筝的时候, 你正在做最好的风扇。 当你的朋友决定用钻石形状的风筝去吹风, 你尝试做一个三角形的风筝。 在试图把风筝粘在一起的时候, 你用70英寸的角度把第一和第二块锁在一起。 第一和第三块之间的角是40英寸。 最后, 你还测量了第二块的长度, 发现它长22英寸。Your kite looks like this:
::你的风筝看起来是这样的:Is there a way to find out, using math, what the length of the third side will be?
::有没有办法用数学找出 第三方的长度是多少?AAS Triangles
::AAS 三角The states: . This is a ratio between the sine of an angle in a triangle and the length of the side opposite that angle to the sine of a different angle in that triangle and the length of the side opposing that second angle.
::状态 : sinAa=sinBb 。 这是三角形角的正弦值与三角形角对面角与该三角形不同角的正弦值和对面第二个角的侧面长度之间的比例 。The Law of Sines allows us to find many quantities of interest in triangles by comparing sides and interior angles as a ratio. One case where we can to use the Law of Sines is when we know two of the angles in a triangle and a non-included side (AAS).
::《辛那斯定律》允许我们通过比较侧面和内侧角度作为比例来发现三角关系中的许多兴趣。 我们可以使用辛那斯定律的一个例子是,我们知道三角关系中的两个角度和没有包括的方面(AAS ) 。Using the Law of Sines.
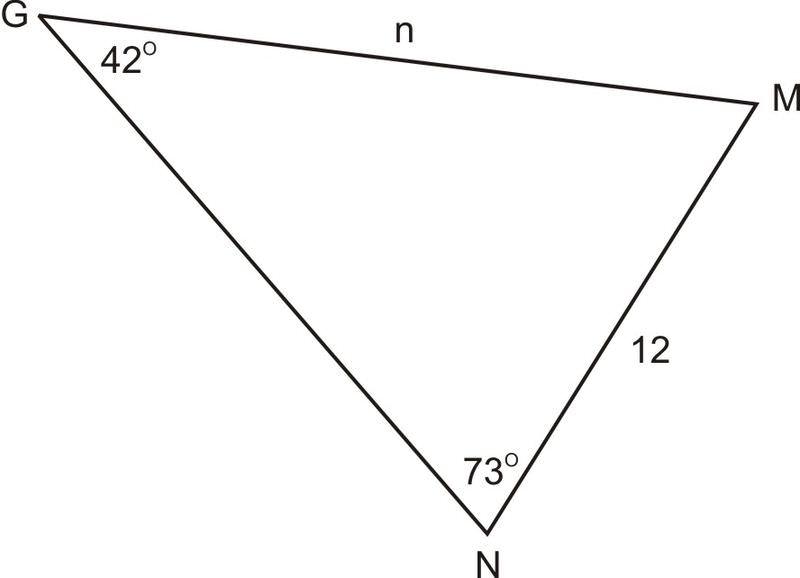
::使用Sines法则。1. Using and . Find .
::1. 使用GMN,G=42,N=73和g=12。Since we know two angles and one non-included side , we can find the other non-included side "> .
::由于我们知道两个角度和一个未包括的方面(g),我们可以找到另一个未包括的方面。
::12sin\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\1715。2. Continuing on from #1, find and .
::2. 继续从#1开始,找到#M和M。is simply . To find side , you can now use either the Law of Sines or . Considering that the Law of Sines is a bit simpler and new, let’s use it. It does not matter which side and opposite angle you use in the ratio with and .
::”M 简单就是 18042736565。要找到侧面,您现在可以使用松树定律,也可以使用。考虑到松树定律比较简单和新,让我们使用它。与 @M 和 m 的比例相比,您使用哪个侧面和相反的角度并不重要。Option 1: and
::备选1:G和g
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}为什么?Option 2: and
::备选2:N和n
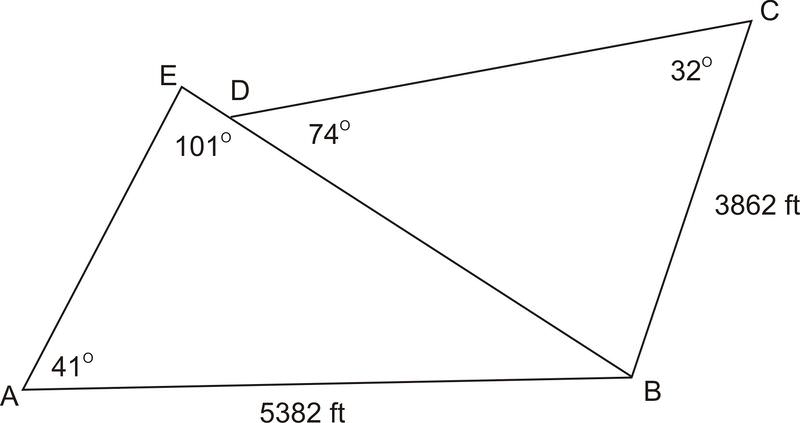
::1715 msin 73 73 1715 msin 73 *1715 sin 65 m=1715 msin *65 75 @sin 73 @m_16.253. A business group wants to build a golf course on a plot of land that was once a farm. The deed to the land is old and information about the land is incomplete. If is 5382 feet, is 3862 feet, is is is and is , what are the lengths of the sides of each triangular piece of land? What is the total area of the land?
::3. 一个商业团体希望在曾经是农场的一块土地上建造高尔夫球场,地契是旧的,有关土地的信息是不完整的,如果AB是5382英尺,BC是3862英尺,AEB是101,BDC是74,EAB是41,DCB是32,三边土地两边的长度是多少?土地的总面积是多少?Before we can figure out the area of the land, we need to figure out the length of each side. In , we know two angles and a non-included side. This is the AAS case. First, we will find the third angle in by using the Triangle Sum Theorem. Then, we can use the Law of Sines to find both and .
::在确定陆地面积之前,我们需要弄清楚每一边的长度。 在 QABE 中, 我们知道两个角度和一个非包含的侧面。 这是 AAS 案例。 首先, 我们会通过使用三角区 Sum Theorem 在 ABE 中找到第三个角度 。 然后, 我们可以使用 Sines 法则来同时找到 AE 和 EB 。
::ABE=180-(41+101)=38sin1015382=sin38AEsin1015382=sin41EBAE(sin101)=5382(sin38)EB(sin101)=5382(sin38)AE=5382(sin38)_101EB=5382(sin101E=515.5英尺EB_359700英尺)Next, we need to find the missing side lengths in . In this triangle, we again know two angles and a non-included side (AAS), which means we can use the Law of Sines. First, let’s find . Since both and measure , is an isosceles triangle. This means that since is 3862 feet, is also 3862 feet. All we have left to find now is .
::接下来,我们需要在 DCB 中找到缺失的侧边长度。 在这个三角形中, 我们再次知道两个角度和一个不包含的侧面( AAS ) , 这意味着我们可以使用Sines 定律 。 首先, 让我们找到 DBC =180- (74+32) = 74\ 。 由于 BDC 和 DB 度量 74 , DCB 是一个等分形三角形。 这意味着自 BC 是 3862 英尺, DC 也是 3862 英尺。 我们现在只能找到 DB 。
::=3862(sin32)DB(sin74)=3862(sin32)DB=3862(sin32)sin74DB2129.0英尺Finally, we need to calculate the area of each triangle and then add the two areas together to get the total area. From the last section, we learned two area formulas, and Heron’s Formula. In this case, since we have enough information to use either formula, we will use since it is less computationally intense.
::最后,我们需要计算每个三角形的面积, 然后将两个区域加在一起才能获得总面积。 从最后一节, 我们学到了两个区域公式, K=12 bcsinA 和 Heron 公式。 在这种情况下, 既然我们有足够的信息可以使用其中任何一个公式, 我们将使用 K=12 bcsinA, 因为计算强度较小 。First, we will find the area of .
::首先,我们将找到AABE地区。:
::亚伯:
::K=12(3375.5)(5382)sin41K=5 959,292.8平方英尺:
::DBC:
::K=12(3862)(3862sin32K=3,951,884.6英尺)The total area is .
::总面积为5,959,292.8+3,951,884.6=9,911,177.4平方英尺。Examples
::实例Example 1
::例1Earlier, you were asked to find the length of the third side of the triangle.
::早些时候,有人要求你找到三角形第三边的长度。Since you know two angles and one non-included side of the kite, you can find the other non-included side using the Law of Sines. Set up a ratio using the angles and side you know and the side you don't know.
::既然您知道风筝的两个角度和一个没有包含的侧面, 您可以使用“ 松树法则” 找到另一个没有包含的侧面。 使用角度和侧面设置比例, 您知道, 以及您不知道的侧面 。
::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么? {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}什么?The length of the dowel rod on the unknown side will be approximately 32 inches.
::不明侧面的围巾杆长度大约为32英寸。Example 2
::例2Find side "d" in the triangle below with the following information:
::在下方三角形中用以下信息查找侧边“d”:e=214.9,D=39.7,E=41.3
::41.3214.9=sin39.7d d=208.0Example 3
::例3Find side "o" in the triangle below with the following information:
::在下方三角形中找到侧边的“o” , 并有以下信息: M=31, O=9, m=15
::9o=sin3115154.6Example 4
::例4Find side "q" in the triangle below with the following information:
::在下方三角形中找到侧边“q”并有以下信息:127,R=21.8,r=3.62。
::=7.8 3.62,q=7.8 3.62,q=7.8 2.8 3.62,q=7.8Review
::回顾In , , , and a=6.
::在ABC, mA=50, mB=34,和a=6。-
Find the length of b.
::查找 b 的长度。 -
Find the length of c.
::查找 c 的长度 。
In , , , and k=14.
::在 @KMS, mK=42, mM=26和k=14。-
Find the length of m.
::查找 m 长度 -
Find the length of s.
::查找 s. 的长度。
In , , , and d=23.
::在“DEF, mD=52, mE=78, d=23”。-
Find the length of e.
::查找 e 的长度。 -
Find the length of f.
::查找 f. 的长度
In , , , and p=20.
::在“PQR”中, mP=2, m79和p=20。-
Find the length of q.
::查找 q 的长度 。 -
Find the length of r.
::查找 r 的长度 。
In , , , and o=12.
::在“DOG”,MD=50,MG=59,O=12。-
Find the length of d.
::查找 d 的长度 。 -
Find the length of g.
::查找 g 的长度。
In , , , and a=8.
::在《禁止酷刑公约》中, mC=82, mT=4和a=8。-
Find the length of c.
::查找 c 的长度 。 -
Find the length of t.
::查找 t 的长度 。
In , , , and s=15.
::在“YOS”, mY=65, mO=72,和S=15。-
Find the length of o.
::查找 o 的长度 。 -
Find the length of y.
::查找 y 的长度。
In , , , and o=19.
::在HCO, mH=87, mC=14,和o=19。-
Find the length of h.
::查找 h. 的长度 -
Find the length of c.
::查找 c 的长度 。
Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -
Find the length of b.