5.8 角度- 角度- 角度- 角度- 角度三角

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节角度- 角度- 角度- 角度- 角度三角形

  折叠 展开

  角度- 角度- 角度- 角度- 角度三角形

  播放段落

  You're eating lunch in the cafeteria one afternoon while working on your math homework. Lately you seem to notice the triangular shapes in everything. At home, at school, with your friends. It seems like triangles are everywhere. And you find yourself trying to apply what you are learning in math class to all of the triangles around you. And today is no exception. As you start to take a bite of your chip, you suddenly recognize that familiar shape - the triangle.
  ::你有一个下午在餐厅吃午餐, 做你的数学作业。 最近你似乎注意到每样东西的三角形。 在家里, 在学校, 和你的朋友在一起。 似乎三角形无处不在。 你发现自己在数学课上学习的东西 应用到周围所有三角形上。 今天也不例外。 当你开始咬一口你的芯片时, 你突然认出了那种熟悉的三角形—— 三角形。

  播放段落

  You estimate the length of one of the sides of the chip to be 3 cm. You also can tell that the angle adjacent to the 3 cm side is $\begin{array}{r}{50}^{\circ }\end{array}$ and the angle adjacent on the other side of the 3 cm edge is $\begin{array}{r}{60}^{\circ }\end{array}$ . Can you find the lengths of the other two sides using techniques from your math class?
  ::您估计芯片两侧的长度为 3 厘米。 您也可以从数学课中找到另外两侧的长度吗 ?

  播放段落

  ASA Triangles
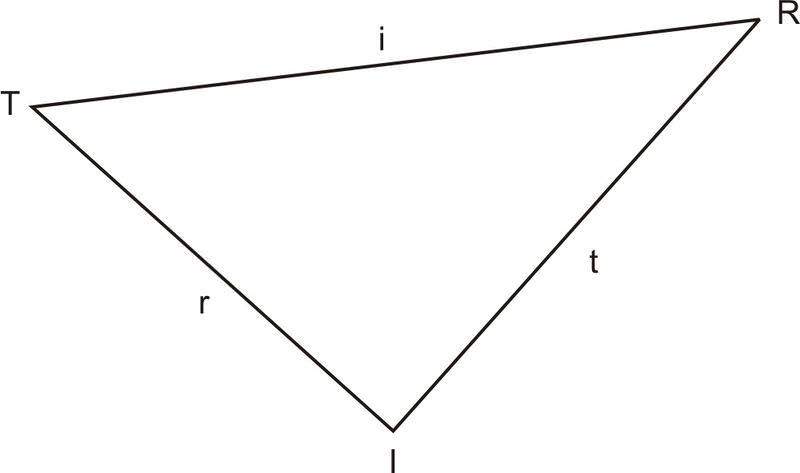
  ::ASA 三角

  播放段落

  The states: $\begin{array}{r}\frac{\sin A}{a}=\frac{\sin B}{b}\end{array}$ . This is a ratio between the sine of an angle in a triangle and the length of the side opposite that angle to the sine of a different angle in that triangle and the length of the side opposing that second angle.
  ::状态 : sinAa=sinBb 。 这是三角形角的正弦值与三角形角对面角与该三角形不同角的正弦值和对面第二个角的侧面长度之间的比例 。

  播放段落

  One case where we use the Law of Sines is when we know two angles in a triangle and the included side (ASA). For instance, in $\begin{array}{r}\mathrm{△}TRI\end{array}$ :
  ::我们使用Sines定律的一个例子是,我们知道三角形和包括的侧面的两个角度(ASA)。

  

  播放段落

  $\begin{array}{r}\mathrm{\angle }T,\mathrm{\angle }R\end{array}$ , and $\begin{array}{r}i\end{array}$ are known
  ::T, R, 和我已知的

  播放段落

  $\begin{array}{r}\mathrm{\angle }T,\mathrm{\angle }I\end{array}$ ,and $\begin{array}{r}r\end{array}$ are known
  ::T, i, r, 和r已知

  播放段落

  $\begin{array}{r}\mathrm{\angle }R,\mathrm{\angle }I\end{array}$ , and $\begin{array}{r}t\end{array}$ are known
  ::R, I, 和 t已知

  播放段落

  In this case, the Law of Sines allows us to find either of the non-included sides.
  ::在此情况下,《辛那法》允许我们找到一个未包括的方面。

  播放段落

  Using the Law of Sines 
  ::使用Sines定律

  播放段落

  1. In the triangle above, $\begin{array}{r}\mathrm{△}TRI,\mathrm{\angle }T={83}^{\circ },\mathrm{\angle }R={24}^{\circ }\end{array}$ , and $\begin{array}{r}i=18.5\end{array}$ . Find the measure of $\begin{array}{r}t\end{array}$ .
  ::1. 在上述三角形上,请找到 t 的度量。

  播放段落

  Since we know two angles and the included side, we can find either of the non-included sides using the Law of Sines. Since we already know two of the angles in the triangle, we can find the third angle using the fact that the sum of all of the angles in a triangle must equal $\begin{array}{r}{180}^{\circ }\end{array}$ .
  ::既然我们知道两个角度和包括的一面,我们就可以用“辛那斯定律”找到一个未包括的两边。 既然我们已经知道三角形的两个角度,我们就可以用三角形中所有角度的总和必须等于180来找到第三个角度。

  播放段落

  $$\begin{array}{rl}\mathrm{\angle }I& =180-(83+24)\\ \mathrm{\angle }I& =180-107\\ \mathrm{\angle }I& ={73}^{\circ }\end{array}$$

  
  ::*I=180 -(83+24)... *I=180 -107 *I=73*

  播放段落

  Now that we know $\begin{array}{r}\mathrm{\angle }I={73}^{\circ }\end{array}$ , we can use the Law of Sines to find $\begin{array}{r}t\end{array}$ .
  ::现在我们知道"I=73"了, 我们可以用辛尼定律来找到t。

  播放段落

  $$\begin{array}{rl}\frac{\sin 73}{18.5}& =\frac{\sin 83}{t}\\ t(\sin 73)& =18.5(\sin 83)\\ t& =\frac{18.5(\sin 83)}{\sin 73}\\ t& \approx 19.2\end{array}$$

  
  ::7318.5=sin83t(sin73)=18.5(sin83t)=18.5(sin83)sin73t19.2

  播放段落

  Notice how we wait until the last step to input the values into the calculator. This is so our answer is as accurate as possible.
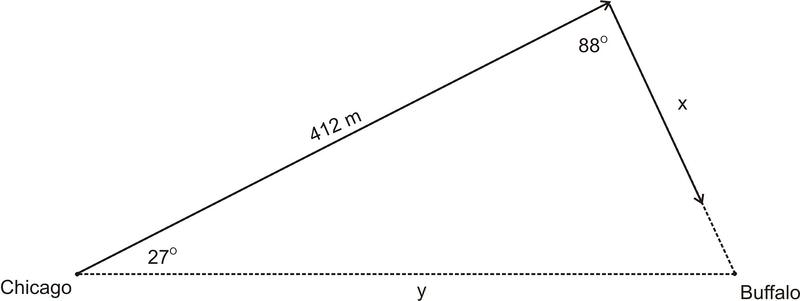
  ::注意我们如何等待最后一步将值输入计算器。 所以我们的答案尽可能准确 。

  播放段落

  2. In order to avoid a large and dangerous snowstorm on a flight from Chicago to Buffalo, pilot John starts out $\begin{array}{r}{27}^{\circ }\end{array}$ off of the normal flight path. After flying 412 miles in this direction, he turns the plane toward Buffalo. The angle formed by the first flight course and the second flight course is $\begin{array}{r}{88}^{\circ }\end{array}$ . For the pilot, two issues are pressing:
  ::2. 为了避免从芝加哥飞往水牛城的航班发生大规模和危险的暴风雪,驾驶员约翰从正常飞行路线出发,从27°Z出发,朝这个方向飞行412英里后,将飞机转向水牛岛。

  播放段落
  1. What is the total distance of the modified flight path?
     ::修改后的飞行路径的总距离是多少?
  播放段落
  2. How much further did he travel than if he had stayed on course?
     ::他旅行的距离比他停留在航道上还远吗?

  

  播放段落

  In order to find the total distance of the modified flight path, we need to know side $\begin{array}{r}x\end{array}$ . To find side $\begin{array}{r}x\end{array}$ , we will need to use the Law of Sines. Since we know two angles and the included side, this is an ASA case. Remember that in the ASA case, we need to first find the third angle in the triangle.
  ::为了找到修改后的飞行路径的总距离,我们需要知道侧面 x。 要找到侧面 x, 我们需要使用Sines 定律 。 由于我们知道两个角度和包含的侧面, 这是 ASA 案例 。 记住在 ASA 案例中, 我们首先需要在三角形中找到第三个角度 。

  播放段落

  $$\begin{array}{rlrl}MissingAngle& =180-(27+88)={65}^{\circ }& & \text{The sum of angles in a triangle is}180\\ \frac{\sin 65}{412}& =\frac{\sin 27}{x}& & \text{Law of Sines}\\ x(\sin 65)& =412(\sin 27)& & \text{Cross multiply}\\ x& =\frac{412(\sin 27)}{\sin 65}& & \text{Divide by sin}65\\ x& \approx 206.4miles\end{array}$$

  
  ::缺少 Angle=180 -( 27+88)=65 三角形中角的和值是 180sin65412=sin27xxx( sin65)=412( sin27)=412( sin27)Cross 乘数=412( sin27)sin65*65Divide by sin 65x206.4英里

  播放段落

  The total distance of the modified flight path is $\begin{array}{r}412+206.4=618.4miles\end{array}$ .
  ::经修改的飞行路径总距离为412+206.4=618.4英里。

  播放段落

  To find how much farther John had to travel, we need to know the distance of the original flight path, $\begin{array}{r}y\end{array}$ . We can use the Law of Sines again to find $\begin{array}{r}y\end{array}$ .
  ::要找到约翰必须走多远, 我们需要知道原始飞行路径的距离, y. 我们可以再次使用辛斯定律来找到y.

  播放段落

  $$\begin{array}{rlrl}\frac{\sin 65}{412}& =\frac{\sin 88}{y}& & \text{Law of Sines}\\ y(\sin 65)& =412(\sin 88)& & \text{Cross multiply}\\ y& =\frac{412(\sin 88)}{\sin 65}& & \text{Divide by}\sin 65\\ y& \approx 454.3miles\end{array}$$

  
  ::辛尼西法(辛尼西法)=412(辛尼西里加88)Cross乘数=412(辛西里加882)65Divide by sinci=65y454.3英里

  播放段落

  John had to travel $\begin{array}{r}618.4-454.3=164.1miles\end{array}$ farther.
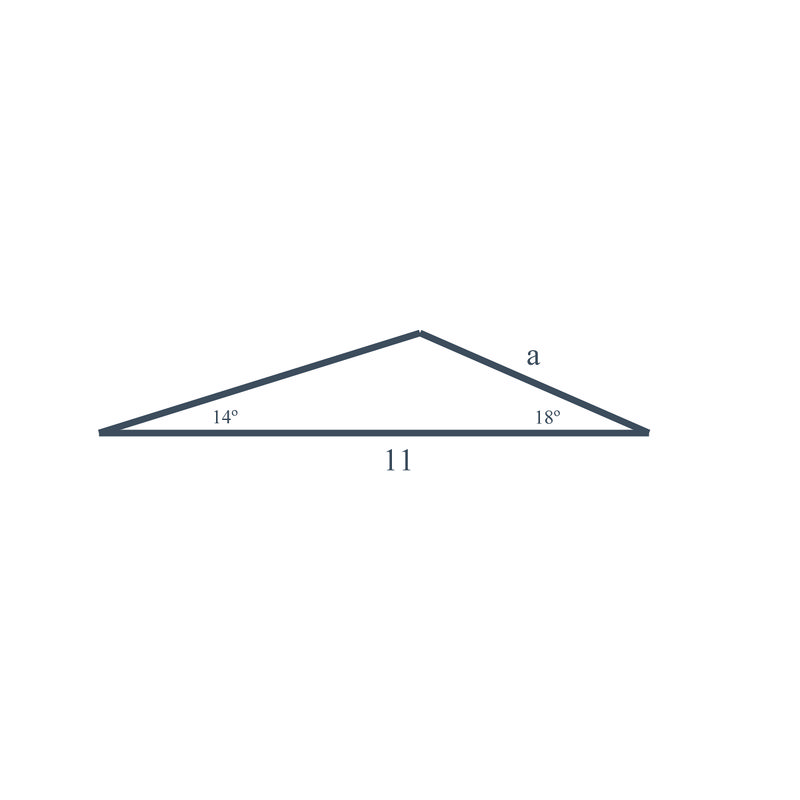
  ::约翰不得不远行618.4-454.3=164.1英里。

  播放段落

  2. In the triangle shown here:
  ::2. 在此处显示的三角形中:

  

  播放段落

  The sides given are $\begin{array}{r}\mathrm{\angle }A={14}^{\circ }\end{array}$ , $\begin{array}{r}\mathrm{\angle }B={18}^{\circ }\end{array}$ , and c = 11. Find the length of side "a".
  ::给出的两边是A=14,B=18,和 c=11。 找出侧“a”的长度。

  播放段落

  Since we know two angles and the included side, we can find either of the non-included sides using the Law of Sines. Since we already know two of the angles in the triangle, we can find the third angle using the fact that the sum of all of the angles in a triangle must equal $\begin{array}{r}{180}^{\circ }\end{array}$ .
  ::既然我们知道两个角度和包括的一面,我们就可以用“辛那斯定律”找到一个未包括的两边。 既然我们已经知道三角形的两个角度,我们就可以用三角形中所有角度的总和必须等于180来找到第三个角度。

  播放段落

  $$\begin{array}{rl}\mathrm{\angle }C& =180-(18+14)\\ \mathrm{\angle }C& =180-32\\ \mathrm{\angle }C& ={148}^{\circ }\end{array}$$

  
  ::*C=180-(18+14)C=180-32*C=148*

  播放段落

  Use the Law of Sines to find the length of side "a":
  ::使用Sines法则 找到侧面的“a”长度 :

  播放段落

  $$\begin{array}{rl}\frac{\sin 14}{a}& =\frac{\sin 148}{11}\\ 11(\sin 14)& =a(\sin 148)\\ a& =\frac{11(\sin 14)}{\sin 148}\\ a& \approx 5.02\end{array}$$

  
  ::-=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find the other two lengths of the triangle. 
  ::早些时候,你被要求 找到另外两个三角形的长度。

  播放段落

  You can use the Law of Sines to find the length of either of the other 2 sides. However, first it is good to note that since the sum of the interior angles of a triangle must equal $\begin{array}{r}{180}^{\circ }\end{array}$ , the third angle in the triangle must measure $\begin{array}{r}{180}^{\circ }-{50}^{\circ }-{60}^{\circ }={70}^{\circ }\end{array}$ .
  ::您可以使用Sines Law 来找到另外两边的长度。 但是, 首先, 值得注意的是, 由于三角形内部角的总和必须等于 180 , 三角形中第三个角必须测量 180 50 60 70 。

  播放段落

  Now to set up the ratios:
  ::现在设置比率 :

  播放段落

  $$\begin{array}{rl}\frac{\sin 60}{a}& =\frac{\sin 70}{3}\\ 3(\sin 60)& =a(\sin 70)\\ a& =\frac{3(\sin 60)}{\sin 70}\\ a& \approx 2.7647\end{array}$$

  
  ::-=====================================================================================================================================================================================================================================================================================================================================================================================================

  播放段落

  The length of one of the other 2 sides is approximately 2.7647 centimeters.
  ::另外两边之一的长度约为2.7647厘米。

  播放段落

  To find the length of the last side:
  ::要找到最后一面的长度 :

  播放段落

  $$\begin{array}{rl}\frac{\sin 50}{b}& =\frac{\sin 70}{3}\\ 3(\sin 50)& =b(\sin 70)\\ b& =\frac{3(\sin 50)}{\sin 70}\\ b& \approx 2.46\end{array}$$

  
  ::-=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

  播放段落

  The length of the other one of the 2 unknown sides is approximately 2.46 centimeters.
  ::两个未知边的另一边的长度约为2.46厘米。

  播放段落

  Example 2
  ::例2

  播放段落

  Find side "a" in the triangle below using the following information: $\begin{array}{r}b=16,A={11.7}^{\circ },C={23.8}^{\circ }\end{array}$
  ::在下方三角形中用以下信息查找侧边“a”:b=16,A=11.7,C=23.8

  

  播放段落

  $\begin{array}{r}\frac{\sin {11.7}^{\circ }}{a}=\frac{\sin {144.5}^{\circ }}{16},a=5.6\end{array}$
  ::一九零七年一月一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一日一夜

  播放段落

  Example 3
  ::例3

  播放段落

  Find side "a" in the triangle below using the following information: $\begin{array}{r}k=6.3,J={16.2}^{\circ },L={40.3}^{\circ }\end{array}$
  ::使用以下信息查找三角形下方的侧边“a” : k=6.3, J=16.2, L=40.3

  

  播放段落

  $\begin{array}{r}\frac{\sin {40.3}^{\circ }}{l}=\frac{\sin {123.5}^{\circ }}{6.3},l=4.9\end{array}$
  ::=40.3l=sin 123.56.3,l=4.9

  播放段落

  Example 4
  ::例4

  播放段落

  Even though ASA and AAS triangles represent two different cases of the Law of Sines, what do they both have in common?
  ::尽管ASA和AAS三角形代表了两个不同的Sines法律案例,但两者有什么共同之处?

  播放段落

  Student answers will vary but they should notice that in both cases you know or can find an angle and the side across from it.
  ::学生的回答会有所不同,但他们应该注意到,在这两种情况下,你都知道或能找到角度和侧面。

  播放段落

  Review
  ::回顾

  播放段落

  In $\begin{array}{r}\mathrm{△}ABC\end{array}$ , $\begin{array}{r}m\mathrm{\angle }A={40}^{\circ }\end{array}$ , $\begin{array}{r}m\mathrm{\angle }B={67}^{\circ }\end{array}$ , and c = 6.
  ::ABC, mA=40, mB=67,c=66

  播放段落
  1. Find $\begin{array}{r}m\mathrm{\angle }C\end{array}$ .
     ::寻找 mC。
  播放段落
  2. Find the length of a.
     ::查找 a 的长度 。
  播放段落
  3. Find the length of b.
     ::查找 b 的长度。

  播放段落

  In $\begin{array}{r}\mathrm{△}DEF\end{array}$ , $\begin{array}{r}m\mathrm{\angle }D={36}^{\circ }\end{array}$ , $\begin{array}{r}m\mathrm{\angle }E={101}^{\circ }\end{array}$ , and f = 11.
  ::在“DEF”, mD=36, mE=101, f=11。

  播放段落
  4. Find $\begin{array}{r}m\mathrm{\angle }F\end{array}$ .
     ::去找MF
  播放段落
  5. Find the length of d.
     ::查找 d 的长度 。
  播放段落
  6. Find the length of e.
     ::查找 e 的长度。

  播放段落

  In $\begin{array}{r}\mathrm{△}BIG\end{array}$ , $\begin{array}{r}m\mathrm{\angle }B={56}^{\circ }\end{array}$ , $\begin{array}{r}m\mathrm{\angle }I={71}^{\circ }\end{array}$ , and g = 23.
  ::在“BIG”中, mB=56, mI=71, g=23。

  播放段落
  7. Find $\begin{array}{r}m\mathrm{\angle }G\end{array}$ .
     ::去找MG
  播放段落
  8. Find the length of b.
     ::查找 b 的长度。
  播放段落
  9. Find the length of i.
     ::查找 i 的长度。

  播放段落

  In $\begin{array}{r}\mathrm{△}APL\end{array}$ , $\begin{array}{r}m\mathrm{\angle }A={79}^{\circ }\end{array}$ , $\begin{array}{r}m\mathrm{\angle }P={40}^{\circ }\end{array}$ , and l = 15.
  ::在 APL, mA=79, mP=40,l=15。

  播放段落
  10. Find $\begin{array}{r}m\mathrm{\angle }L\end{array}$ .
      ::去找ML
  播放段落
  11. Find the length of a.
      ::查找 a 的长度 。
  播放段落
  12. Find the length of p.
      ::查找 p.

  播放段落

  In $\begin{array}{r}\mathrm{△}SAU\end{array}$ , $\begin{array}{r}m\mathrm{\angle }S=5^{\circ }\end{array}$ , $\begin{array}{r}m\mathrm{\angle }A={99}^{\circ }\end{array}$ , and u = 21.
  ::在 SAU 中, mS=5, mA=99, u=21

  播放段落
  13. Find $\begin{array}{r}m\mathrm{\angle }U\end{array}$ .
      ::去找妈妈
  播放段落
  14. Find the length of s.
      ::查找 s. 的长度。
  播放段落
  15. Find the length of a.
      ::查找 a 的长度 。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。