Course: 5.9 可能具有双侧角三角形的三角形

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

可能有侧侧侧角三角形的三角形

Your team has just won the flag in a flag football tournament at your school. As a reward, you get to take home the flag and keep it until the next game, when the other team will try to win it back. The flag looks like this:
::你们的球队刚刚在你们学校的一场国旗足球锦标赛中赢得了国旗。作为奖赏,你们可以把国旗带回家,直到下一场比赛,然后另一队将试图赢回来。

It makes an isosceles triangle. You start to wonder how many different possible triangles there are for different lengths of sides. For example, if you make an oblique triangle that has a given angle greater than ninety degrees, how many ways are there to do this? Can you determine how many different possible triangles there are if the triangle is an isosceles triangle?
::它会形成一个等分形三角形。您开始想知道不同的边边有多少个不同可能的三角形。例如, 如果您制造一个角大于90度的斜角三角形, 那么可以用多少种方法来做到这一点 ? 您能否确定如果三角形是一个等分形三角形, 那么可能有多少个不同的三角形 ?

SSA Triangles
::SSA 三角

In Geometry, you learned that two sides and a non-included angle do not necessarily define a unique triangle.
::在几何学中,你了解到,两面和未包含的角度并不一定定义一个独特的三角形。

Consider the following cases given $\begin{aligned} a, b \end{aligned}$ , and $\begin{aligned} ∠ A \end{aligned}$ :
::考虑下列情况a、b和A:

Case 1: No triangle exists $\begin{aligned} (a < b) \end{aligned}$
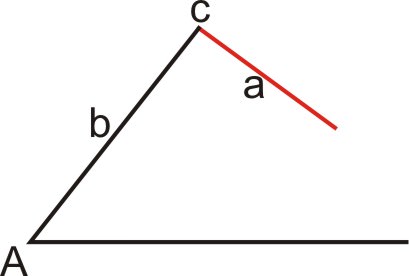
::案件1:不存在三角关系(a <b)

In this case $\begin{aligned} a < b \end{aligned}$ and side $\begin{aligned} a \end{aligned}$ is too short to reach the base of the triangle. Since no triangle exists, there is no solution.
::在此情况下, <b 和侧面 a 的长度太短, 无法到达三角形的底部。由于不存在三角形, 因此没有解决方案。

Case 2: One triangle exists $\begin{aligned} (a < b) \end{aligned}$
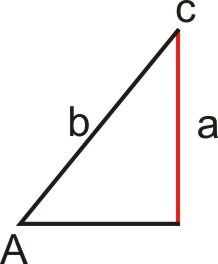
::案例2:存在一个三角形(a<b)

In this case, $\begin{aligned} a < b \end{aligned}$ and side $\begin{aligned} a \end{aligned}$ is perpendicular to the base of the triangle. Since this situation yields exactly one triangle, there is exactly one solution.
::在此情况下, <b 和侧面 a 与三角形底部垂直。由于此情况产生一个三角形, 完全只有一个解决方案。

Case 3: Two triangles exist $\begin{aligned} (a < b) \end{aligned}$
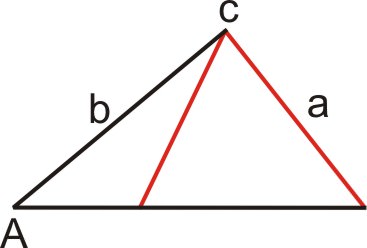
::案例3:存在两个三角形(a < (b))

In this case, $\begin{aligned} a < b \end{aligned}$ and side $\begin{aligned} a \end{aligned}$ meets the base at exactly two points. Since two triangles exist, there are two solutions.
::在此情况下, a < b 和 a 的侧面在精确的两点满足基点。由于存在两个三角形, 有两个解决方案。

Case 4: One triangle exists $\begin{aligned} (a = b) \end{aligned}$
::案例4:存在一个三角形(a=b)

In this case $\begin{aligned} a = b \end{aligned}$ and side $\begin{aligned} a \end{aligned}$ meets the base at exactly one point. Since there is exactly one triangle, there is one solution.
::在此情况下 a=b 和侧向a 与基点完全匹配一个点。因为完全只有一个三角形, 只有一个解决方案。

Case 5: One triangle exists $\begin{aligned} (a > b) \end{aligned}$
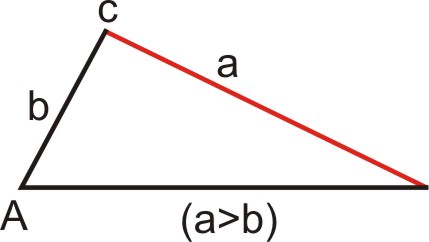
::案例5:存在一个三角形(a>b)

In this case, $\begin{aligned} a > b \end{aligned}$ and side $\begin{aligned} a \end{aligned}$ meets the base at exactly one point. Since there is exactly one triangle, there is one solution.
::在此情况下, a> b 和侧面与基点完全匹配一个点。由于完全只有一个三角形, 只有一个解决方案。

Case 3 is referred to as the Ambiguous Case because there are two possible triangles and two possible solutions. One way to check to see how many possible solutions (if any) a triangle will have is to compare sides $\begin{aligned} a \end{aligned}$ and $\begin{aligned} b \end{aligned}$ . If you are faced with the first situation, where $\begin{aligned} a < b \end{aligned}$ , we can still tell how many solutions there will be by using $\begin{aligned} a \end{aligned}$ and $\begin{aligned} b \sin A \end{aligned}$ .
::案例3被称为“模糊案例”,因为有两种可能的三角形和两种可能的解决方案。检查三角形将有多少可能的解决方案(如果有的话)的一种方法是比较a和b。如果你面临第一种情况,即 <b,我们仍能通过使用 a 和 bsina 来判断有多少解决方案。

	If:	Then:
a.	$\begin{aligned} a < b \end{aligned}$	No solution, one solution, two solutions
i.	$\begin{aligned} a < b \sin A \end{aligned}$	No solution
ii.	$\begin{aligned} a = b \sin A \end{aligned}$	One solution
iii.	$\begin{aligned} a > b \sin A \end{aligned}$	Two solutions
b.	$\begin{aligned} a = b \end{aligned}$	One solution
c.	$\begin{aligned} a > b \end{aligned}$	One solution

Identifying Triangles
::辨别三角三角形

For the following problems, determine if the sides and angles given determine no, one or two triangles.
::对于下列问题,确定所给方和角度是否确定为否,一个或两个三角形。

1. The set contains an angle, its opposite side and the side between them.
::1. 这套装置包含一个角度,即其对面和两侧之间的角。

$\begin{aligned} a = 5, b = 8, A = {62.19}^{\circ} \end{aligned}$
::a=5,b=8,A=62.19

$\begin{aligned} 5 < 8, 8 \sin {62.19}^{\circ} = 7.076 \end{aligned}$ . So $\begin{aligned} 5 < 7.076 \end{aligned}$ , which means there is no solution.
::5<8,8sin62.197.076. 所以5<7.076,这意味着没有解决办法。

2. The set contains an angle, its opposite side and the side between them.
::2. 这套装置包含一个角度,即其对面和两侧之间的角。

$\begin{aligned} c = 14, b = 10, B = {15.45}^{\circ} \end{aligned}$
::c=14,b=10,B=15.45

Even though $\begin{aligned} a, b \end{aligned}$ and $\begin{aligned} ∠ A \end{aligned}$ is not used in this example, follow the same pattern from the table by multiplying the non-opposite side (of the angle) by the angle.
::即使本例未使用 a、b 和 A, 也照样从表格中采用相同的模式, 将非对面侧( 角度) 乘以角度。

$\begin{aligned} 10 < 14, 14 \sin {15.45}^{\circ} = 3.73 \end{aligned}$ . So $\begin{aligned} 10 > 3.73 \end{aligned}$ , which means there are two solutions.
::10<14,14sin15.453.73。 10>3.73, 这意味着有两种解决办法。

3. The set contains an angle, its opposite side and the side between them.
::3. 这套装置包含一个角度,即其对面和两侧之间的角。

$\begin{aligned} d = 16, g = 11, D = {44.94}^{\circ} \end{aligned}$
::d=16,g=11,D=44,94

$\begin{aligned} 16 > 11 \end{aligned}$ , there is one solution.
::16>11,有一个解决办法。

Examples
::实例

Example 1
::例1

Earlier, you were given a problem about a triangle.
::早些时候,有人给了你一个三角形的问题。

As you now know, when two sides of a triangle with an included side are known, and the lengths of the two sides are equal, there is one possible solution. Since an isosceles triangle meets these criteria, there is only one possible solution.
::正如你现在所知道的,当三角形中包含一方的两面已知,而两边的长度相等时,就有一个可能的解决办法。由于一个等分三角形符合这些标准,只有一个可能的解决办法。

Example 2
::例2

Determine how many solutions there would be for a triangle based on the given information and by calculating $\begin{aligned} b \sin A \end{aligned}$ and comparing it with $\begin{aligned} a \end{aligned}$ . Sketch an approximate diagram for each problem in the box labeled “diagram.”
::依据给定的信息,确定三角形将有多少解决方案, 计算 bsinaA, 并将其与 a 进行比较。绘制标有“ 图表” 标签的框中每个问题的大致图表。

$\begin{aligned} A = {32.5}^{\circ}, a = 26, b = 37 \end{aligned}$
::A=32.5,a=26,b=37

$\begin{aligned} A = {32.5}^{\circ}, a = 26, b = 37 \end{aligned}$ $\begin{aligned} 26 > 19.9 \end{aligned}$ 2 solutions
::A=32.5,a=26,b=3726>19.9 2 溶液

Example 3
::例3

$\begin{aligned} A = {42.3}^{\circ}, a = 16, b = 26 \end{aligned}$
::A=42.3,a=16,b=26

$\begin{aligned} A = {42.3}^{\circ}, a = 16, b = 26 \end{aligned}$ $\begin{aligned} 16 < 17.5 \end{aligned}$ 0 solutions
::A=42.3,a=16,b=2616<17.50溶液

Example 4
::例4

$\begin{aligned} A = {47.8}^{\circ}, a = 13.48, b = 18.2 \end{aligned}$
::A=47.8,a=13.48,b=18.2

$\begin{aligned} A = {47.8}^{\circ}, a = 13.48, b = 18.2 \end{aligned}$ $\begin{aligned} 13.48 = 13.48 \end{aligned}$ 1 solution
::A=47.8,a=13.48,b=18.213.48=13.48 1溶液

Review
::回顾

Determine if the sides and angle given determine no, one or two triangles. The set contains an angle, its opposite side and another side of the triangle.
::确定给定的边和角度是否确定为否, 一个或两个三角形。集包含一个角度, 其对面和三角形的另一侧。

$\begin{aligned} a = 6, b = 6, A = 45^{\circ} \end{aligned}$
::a=6,b=6,A=45

$\begin{aligned} a = 4, b = 7, A = 115^{\circ} \end{aligned}$
::a=4,b=7,A=115

$\begin{aligned} a = 5, b = 2, A = 68^{\circ} \end{aligned}$
::a=5,b=2,A=68

$\begin{aligned} a = 7, b = 6, A = 34^{\circ} \end{aligned}$
::a=7,b=6,A=34

$\begin{aligned} a = 5, b = 3, A = 89^{\circ} \end{aligned}$
::a=5,b=3,A=89

$\begin{aligned} a = 4, b = 4, A = 123^{\circ} \end{aligned}$
::a=4,b=4,A=123

$\begin{aligned} a = 6, b = 8, A = 57^{\circ} \end{aligned}$
::a=6,b=8,A=57

$\begin{aligned} a = 4, b = 9, A = 24^{\circ} \end{aligned}$
::a=4,b=9,A=24

$\begin{aligned} a = 12, b = 11, A = 42^{\circ} \end{aligned}$
::a=12,b=11,A=42

$\begin{aligned} a = 15, b = 17, A = 96^{\circ} \end{aligned}$
::a=15,b=17,A=96

$\begin{aligned} a = 9, b = 10, A = 22^{\circ} \end{aligned}$
::a=9,b=10,A=22

In $\begin{aligned} △ A B C \end{aligned}$ , a=4, b=5, and $\begin{aligned} m ∠ A = 32^{\circ} \end{aligned}$ . Find the possible value(s) of c.
::在 ABC 中, a= 4, b=5, mA=32 。查找 c 的可能值。

In $\begin{aligned} △ D E F \end{aligned}$ , d=7, e=5, and $\begin{aligned} m ∠ D = 67^{\circ} \end{aligned}$ . Find the possible value(s) of f.
::在 DEF 中, d= 7, e= 5, mD= 67 。找出 f 的可能值。

In $\begin{aligned} △ K Q D \end{aligned}$ , $\begin{aligned} m ∠ K = 20^{\circ} \end{aligned}$ , k=24, and d=31. Find $\begin{aligned} m ∠ D \end{aligned}$ .
::在 @QQD, mQK=20, k=24, 和 d=31。找到 mQD 。

In $\begin{aligned} △ M R S \end{aligned}$ , $\begin{aligned} m ∠ M = 70^{\circ} \end{aligned}$ , m=44, and r=25. Find $\begin{aligned} m ∠ R \end{aligned}$ .
::在 MRS 中, mM=70, m=44, r=25。找到 mR 。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

可能有侧侧侧角三角形的三角形

SSA Triangles ::SSA 三角

Identifying Triangles ::辨别三角三角形

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)