Course: 2.8 界定关系和职能

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 界定关系和职能

Collapse Expand
界定关系和职能
On a road trip, you stop at a vending machine during a lunch break. Each item in the vending machine has a unique code that consists of a letter followed by a number. No two items in the machine are the same. Is the vending machine an example of a function ?
::在一次公路旅行中,您在午餐休息期间在自动售货机停靠一个自动售货机。自动售货机中的每件物品都有独特的代码,由字母和号码组成。机器中无两件物品是相同的。自动售货机是功能的示例吗?

Relations and Functions
::关系和职能

Functions are a very important part of Algebra II. From this point on, we are going to study several different types of functions: linear, quadratic, cubic, polynomial , rational and trigonometric.
::函数是代数II非常重要的一部分。从这一点开始,我们将研究几种不同类型的函数:线性、四方形、立方体、多元性、合理性和三角性。

First, every set of points is called a relation . A relation is a grouped set of points that relate, or have something in common with each other. Here are a few examples of relations.
::首先,每一组要点都被称为关系。关系是一组相关或有共同点的一组要点。以下是几个关系的例子。

$\begin{aligned} {(3, - 2), (- 4, - 5), (7, - 2), (9, 1)} & {(- 4, 1), (0, 3), (0, 0), (6, - 7)} & y = \sqrt{x + 6} \\ y = - 2 x + 3 & x^{2} + y^{2} = 9 & 3 y - x^{2} + 4 x = 15 \end{aligned}$

::{(3)-2,(-4)-5,(7)-2,(9)-1}(4),(1)3,(0),(0),(6)-7)}y=x+6y×2x+3x2+y2=93-x2+4x=15

Whenever we talk about a set of points, the { }, or brackets are used. In the examples above, there are two sets of points. All 6 of these sets or equations are examples of relations. Relations also have an input and an output. Typically, all inputs are the $\begin{aligned} x - \end{aligned}$ values (and can be called the domain ), and all outputs are the $\begin{aligned} y - \end{aligned}$ values (and can be called the range ). The input could also be considered the independent variable and the output would be the dependent variable. Again, the $\begin{aligned} y - \end{aligned}$ value depends on the value of $\begin{aligned} x \end{aligned}$ . As in the equation of the line, above, if we plug in -1 for $\begin{aligned} x \end{aligned}$ , then we can determine what $\begin{aligned} y \end{aligned}$ is.
::每当我们谈论一组点, {} 或括号时, 都会使用。在以上示例中, 有两组点。所有六组或方程式都是关系的例子。关系中也有输入和输出。通常, 所有输入都是 x - 值( 也可以称为域) , 所有输出都是 y - 值( 也可以称为范围 ) 。输入也可以被视为独立的变量, 输出也会是依附变量。另外, y - 值取决于 x 值。与以上线条的方程式一样, 如果我们插入 x - 1, 那么我们可以确定什么是 y 。

A more specific type of relation is a function. A function is a relation where there is exactly one output for every input. It cannot be a function if at least one input has more than one output. Simply stated, the $\begin{aligned} x - \end{aligned}$ values of a function cannot repeat. When an equation is a function, $\begin{aligned} y \end{aligned}$ is sometimes rewritten as $\begin{aligned} f (x) \end{aligned}$ (pronounced " $\begin{aligned} f \end{aligned}$ of $\begin{aligned} x \end{aligned}$ "). $\begin{aligned} f (x) \end{aligned}$ is the . $\begin{aligned} f (x) \end{aligned}$ will be used more in later chapters.
::更具体的关系类型是一个函数。一个函数是每个输入都有一个输出的关联。如果至少一个输入有一个以上的输出,则该函数不能是一个函数。简单地说,一个函数的 x - 值不能重复。当一个公式是一个函数时,y 有时被重写成 f(x) (被发号为“f of x”)。f(x) 是 .f(x) 将在后面的章节中使用更多。

Let's compare {(3, -2), (-4, -5), (7, -2), (9, 1)} and {(-4, 1), (0, 3), (0, 0), (6, -7)} from above. One is a function and one is not. Which one is the function?
::让我们比较{( 3) , (4) , (5) , (7), (2), (9, 1) 和 {( 4) 1, (0) , (3) , (0) , (0) , (6) , (7) 。一个是函数, 一个不是函数。哪一个函数?

Look in each set to see if the $\begin{aligned} x - \end{aligned}$ values repeat at all. In the second set of points, the $\begin{aligned} x - \end{aligned}$ value, 0, is repeated in the second and third points. There is not exactly one output for this value. That means the second set of points is not a function. The first set is.
::在每个集中查看 x - 值重复是否重现。在第二组点中, X - 值 0 在第二和第三点中重复。这个值没有完全的输出。这意味着第二组点不是一个函数。第一组是。

Below are input/output tables. Let's determine which table represents a function.
::下面是输入/产出表。让我们确定哪个表格代表函数。

a)

::a) (a)

b)

:b) b)

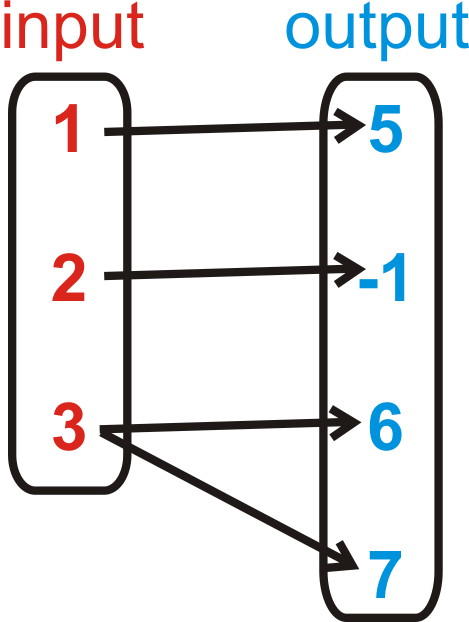
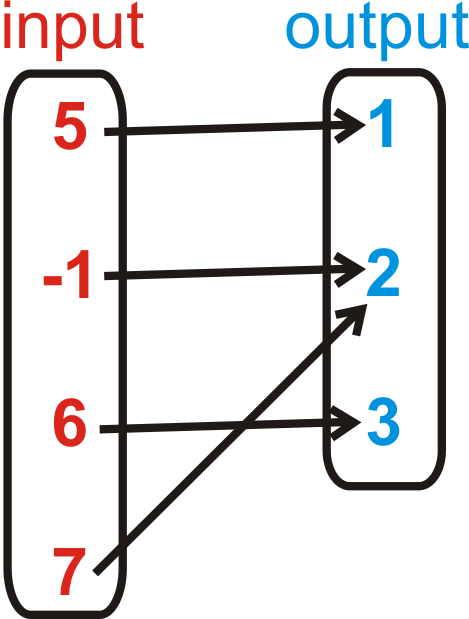
Think back to the definition of a function, “it cannot be a function if at least one input has more than one output.” a) has one input that has more than one output. Therefore , it is not a function. b) does not have an input with two different outputs. Therefore, it is a function.
::回想一个函数的定义,“如果至少一个输入有一个以上的输出,则该函数不能是一个函数。” a)有一个具有多个输出的输入。因此,它不是一个函数。b)没有有两个不同输出的输入。因此,它是一个函数。

Another way to approach these problems is to write out the points that are created and then determine if the $\begin{aligned} x - \end{aligned}$ values repeat. For instance , in part a, the points would be {(1, 5), (2, -1), (3, 6), (3, 7)}. 3 is repeated, meaning it is not a function.
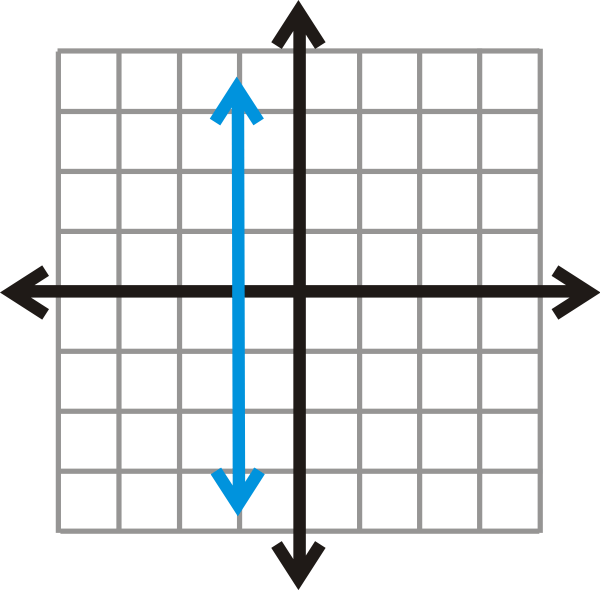
::解决这些问题的另一种方法是写出创建的点,然后确定 x- 值是否重复。例如, 在 a 部分中, 点为 {( 1 、 5 、 2 、 1 、 ( 3 、 6 、 ( 3 、 7 ) 。 ) 3 重复, 意思是它不是一个函数。

We can also apply this idea to equations. Every equation is a relation, but not every equation is a function. The easiest way to determine if an equation is a function is to do the Vertical Line Test . The Vertical Line Test will help you determine if any $\begin{aligned} x - \end{aligned}$ values repeat. First, plot or graph the equation. Then draw several vertical lines. If the graph of the equation touches any vertical line more than once, it is not a function. This works because all vertical lines are in the form $\begin{aligned} x = a \end{aligned}$ , so the $\begin{aligned} x - \end{aligned}$ value for any vertical line will always be the same. The Vertical Line Test tells us if any $\begin{aligned} x - \end{aligned}$ values repeat within a graphed relation.
::我们也可以对方程式应用这个概念。每个方程式是一个关系, 但并不是每个方程式都是一个函数。确定一个方程式是否是一个函数的最简单方式是进行垂直线测试。垂直线测试将有助于您确定是否有任何 x- 值重复。首先, 绘制方程式或图形。然后绘制数条垂直线。如果方程式的图形不止一次触动任何垂直线, 它不是一个函数。这是有效的, 因为所有垂直线都是表 x=a, 因此任何垂直线的x- 值总是相同的。垂直线测试告诉我们在图形关系中是否有 X- 值重复。

Now, let's determine if the equation $\begin{aligned} x^{2} + y^{2} = 9 \end{aligned}$ represents a function.
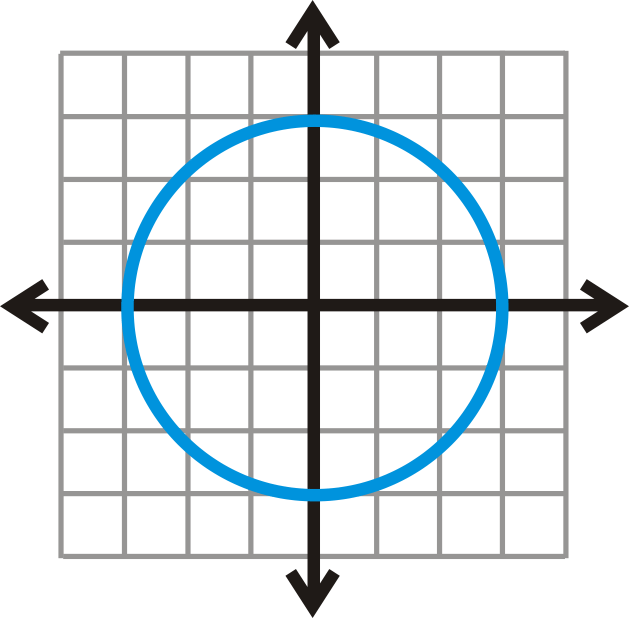
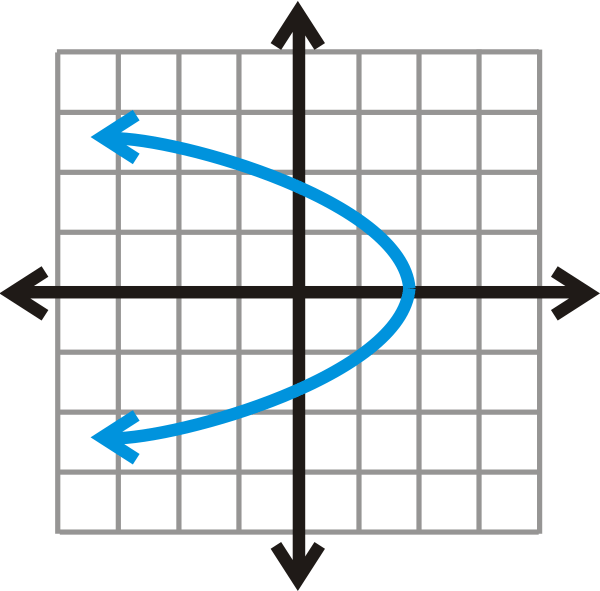
::现在,让我们确定公式 x2+y2=9 是否代表函数。

The graph of $\begin{aligned} x^{2} + y^{2} = 9 \end{aligned}$ is a circle with radius 3.
::x2+y2=9的图形是一个半径为3的圆形。

Drawing vertical lines through the circle, we see that it touches them twice.
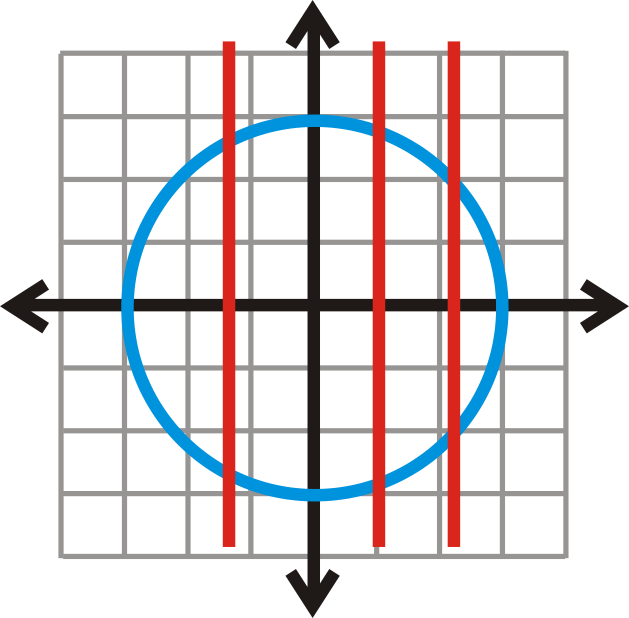
::在圆上画垂直线,我们看到它两次触碰它们。

This tells us that a circle is not a function.
::这告诉我们圆不是函数。

However, if we solve the equation for $\begin{aligned} y \end{aligned}$ , we get $\begin{aligned} y = \pm \sqrt{- x^{2} + 9} \end{aligned}$ or $\begin{aligned} y = \sqrt{- x^{2} + 9} \end{aligned}$ and $\begin{aligned} y = - \sqrt{- x^{2} + 9} \end{aligned}$ . These two equations separately are functions. Think of them as the top and bottom halves of the circle.
::然而,如果我们解决y的方程式, 我们就会得到 y x2+9 或 y x2+9 和 y x2+9 。这两个方程式是独立的函数。把它们想象成圆的顶部和底部。

Examples
::实例

Example 1
::例1

Earlier, you were asked if the vending machine is an example of a function.
::早些时候,有人问你自动售货机是否是一个函数的例子。

Each input (a letter/number combination) into the vending machine results in one and only one item. Since none of the items appear more than once in the vending machine, it is an example of a function.
::自动售货机的每个输入(字母/数字组合)只产生一个项目,因为没有一个项目在自动售货机中出现一次以上,所以它是一个函数的示例。

Example 2
::例2

Determine if the following relation is a function: {(3, -5), (8, 1), (-3, -3), (5, 1)}. Briefly explain your answer.
::确定以下关系是否为函数 {( 3, - 5) (8, 1), (3, 3, 3), (5, 1)}。简要解释您的答复。

Yes, the $\begin{aligned} x - \end{aligned}$ values do not repeat.
::是的, x - 值不重复。

Example 3
::例3

Determine if the following relation is a function: {(9, -2), (0, 0), (7, 4), (9, 3)}. Briefly explain your answer.
::确定以下关系是否是一个函数 {( 9) , (2) , (0) , (7, 4), (9, 3) 。简要解释您的答复。

No, there are two 9’s in the $\begin{aligned} x - \end{aligned}$ values.
::不,x-价值中有两个9。

Example 4
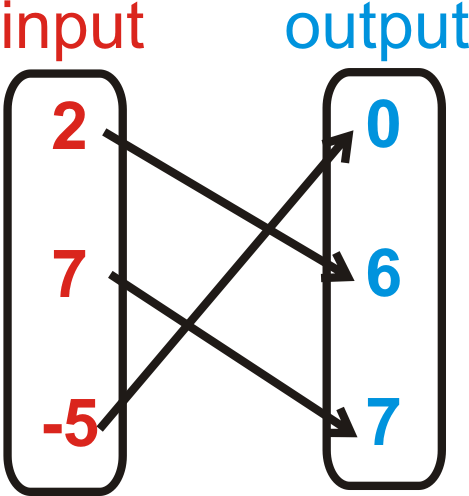
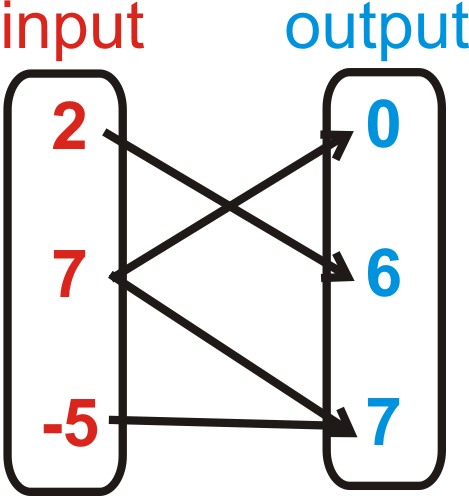
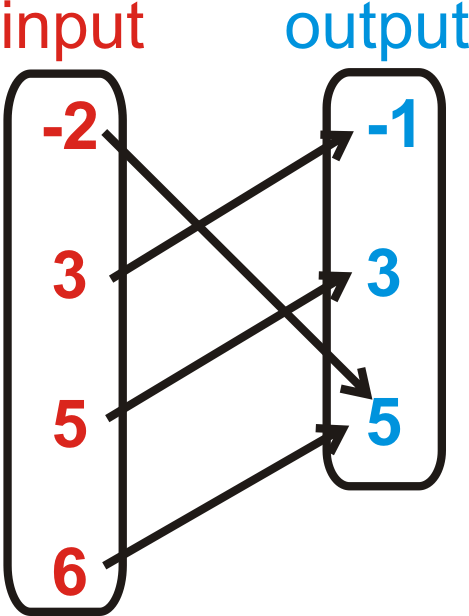
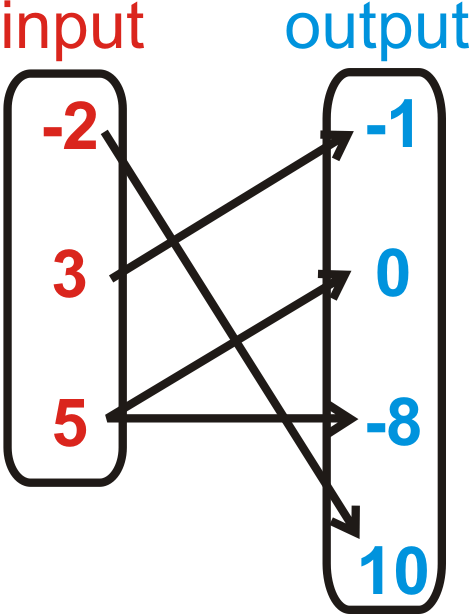
::例4

Determine if the relation below is a function. Briefly explain your answer.
::确定下面的关联是否是一个函数。简要解释您的答复。

Yes, all the outputs have different inputs.
::是的,所有产出都有不同的投入。

Example 5
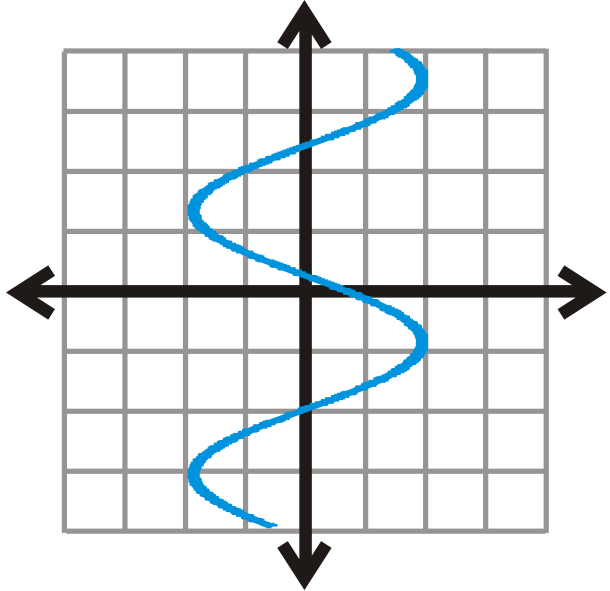
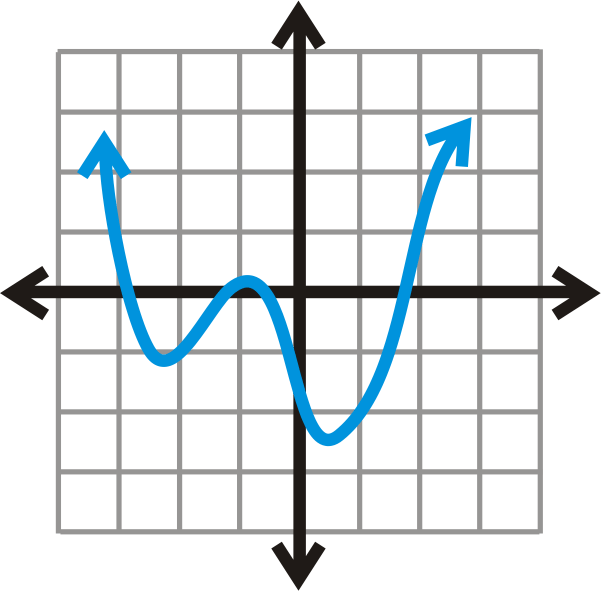
::例5

Determine if the relation below is a function. Briefly explain your answer.
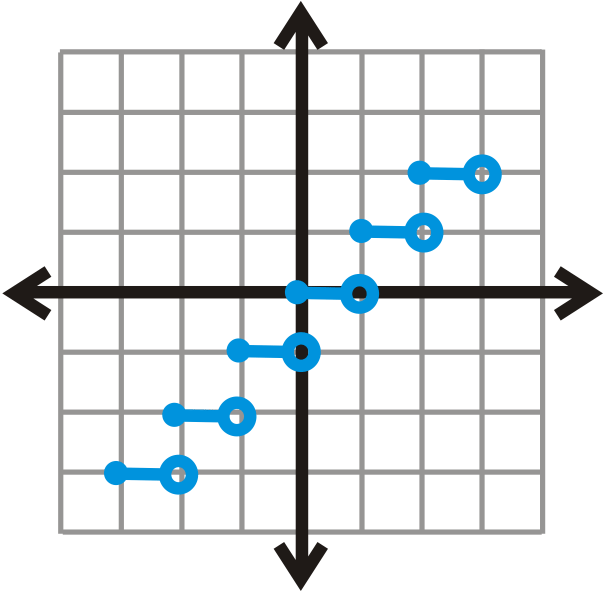
::确定下面的关联是否是一个函数。简要解释您的答复。

Yes, this graph passes the Vertical Line Test. Any vertical line touches this graph once.
::是的, 此图通过垂直线测试。任何垂直线都接触过此图一次。

Review
::回顾

Determine if the following relations are functions. Briefly explain your answer.
::确定以下关系是否为函数。简要解释您的答复。

{(3, 4), (5, 6), (7, 8), (9, 10)}

{(-9, -10), (4, -5), (6, -5), (4, -10)}

{(-5, -7), (0, 4), (-5, 3), (9, 4)}

{(3, -12), (6, -1), (-10, 5), (-2, 9)}

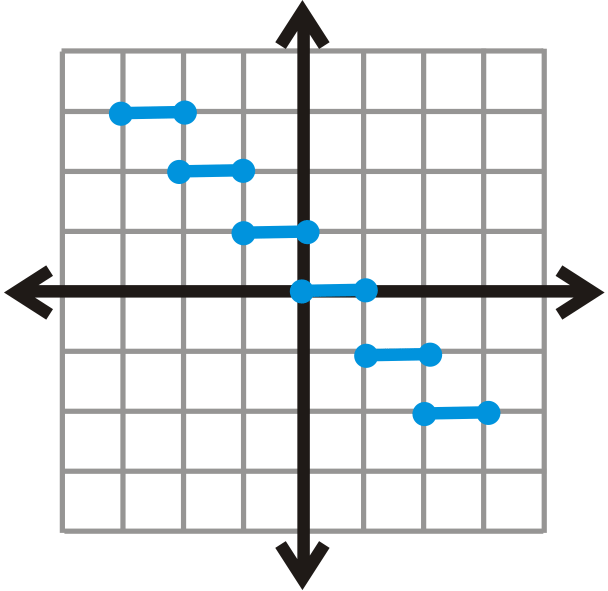
HINT: Recall that with open circles, the point is not included.
::HINT:回顾,在开放的圆圈中,这一点没有包括在内。

For problems 17-19, determine if the following lines are functions.
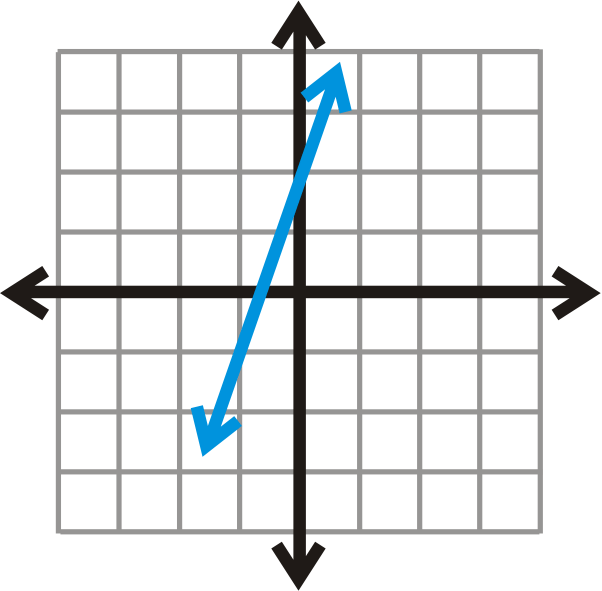
::对于第17-19号问题,确定以下几行是否为职能。

$\begin{aligned} y = - 3 x - 1 \end{aligned}$
::y3x-1

$\begin{aligned} y = \frac{2}{3} x + 6 \end{aligned}$
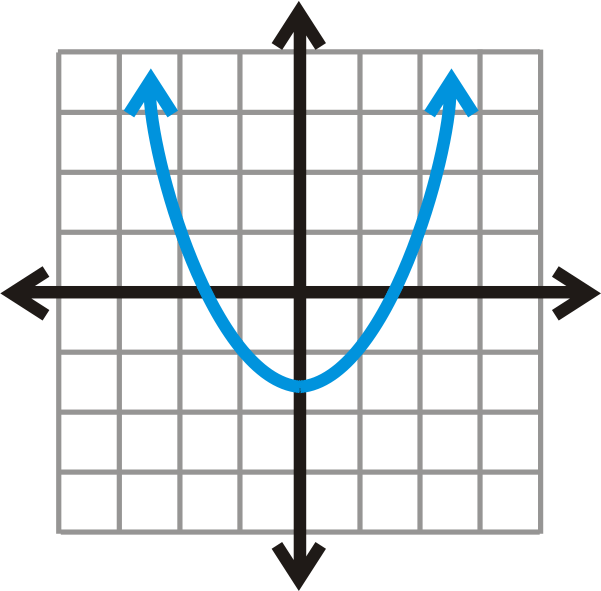
::y=23x+6 y=23x+6

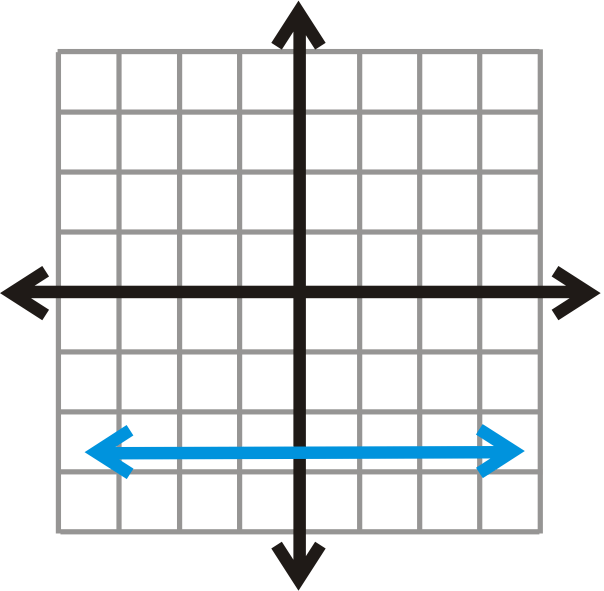
$\begin{aligned} y = - 2 \end{aligned}$
::y2

Is $\begin{aligned} x = 4 \end{aligned}$ a function? Why or why not?
::x=4 是函数吗? 为什么或为什么不是?

From problems 17-20, what can you conclude about linear equations?
::从问题17 -20, 你能得出什么结论关于线性方程?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

界定关系和职能

Relations and Functions ::关系和职能

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Relations and Functions
::关系和职能

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)