课程： 5.10 《锡纳法》

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节Sines法律

折叠展开
Sines法律
While working in art class you are trying to design pieces of glass that you will eventually fit together into a sculpture. You are drawing out what you think will be a diagram of one of the pieces. You have a side of length 14 inches, and side of length 17 inches, and an angle next to the 17 in side of $\begin{aligned} 35^{\circ} \end{aligned}$ (not the angle between the 14 in and 17 in pieces, but the one at the other end of the 17 in piece). Your diagram looks like this:
::在艺术类中工作的时候, 您正在尝试设计玻璃碎片, 您最终会把玻璃碎片放在一个雕塑中。您正在绘制您认为其中一块碎片的图表。您的边长为 14 英寸, 边长为 17 英寸, 边长为 17 英寸, 边近于 17 英寸, 边距为 35 英寸( 不是 14 和 17 之间的角度, 而是 17 段的另一端的角 ) 。您的图表是这样的 :

It occurs to you that you could use your knowledge of math to find out if you are going to be able to finish the drawing and make a piece that could actually be built.
::你会想到,你可以利用数学知识来了解你是否能够完成绘画并制作一个可以实际建造的作品。

Can you figure out how to do this?
::你能想出办法吗?

Law of Sines
::Sines法律

In $\begin{aligned} △ A B C \end{aligned}$ below, we know two sides and a non-included angle. Remember that the Law of Sines states: $\begin{aligned} \frac{\sin A}{a} = \frac{\sin B}{b} \end{aligned}$ . Since we know $\begin{aligned} a, b \end{aligned}$ , and $\begin{aligned} ∠ A \end{aligned}$ , we can use the Law of Sines to find $\begin{aligned} ∠ B \end{aligned}$ . However, since this is the SSA case, we have to watch out for the Ambiguous case. Since $\begin{aligned} a < b \end{aligned}$ , we could be faced with situations where either no possible triangles exist, one possible triangle exists, or two possible triangles exist.
::在下面的 QABC 中,我们知道两面, 还有一个没有包含的角度。记住, Sines 法则指出: sina=sinBb。由于我们知道 a, b 和 A, 我们可以使用 Sines 法则来找到 B。但是, 由于这是 SSA 案例, 我们必须注意这个模糊的个案。从 a < b > 开始, 我们可能会遇到这样的情况: 要么没有可能的三角形, 一个可能的三角形, 或者两个可能的三角形。

To find out how many solutions there are in an ambiguous case, compare the length of $\begin{aligned} a \end{aligned}$ to $\begin{aligned} b \sin A \end{aligned}$ . If $\begin{aligned} a < b \sin A \end{aligned}$ , then there are no solutions. If $\begin{aligned} a = b \sin A \end{aligned}$ , then there is one solution. If $\begin{aligned} a > b \sin A \end{aligned}$ , then there are two solutions.
::要找到一个模糊的案例中有多少解决方案, 请比较 a 和 bsina 的长度。如果 a 和 bsina 的长度, 那么就没有解决方案。如果 a = bsina, 那么只有一个解决方案。如果 a 和 bsina 的长度, 那么有两个解决方案。

Let's take a took at a few problems where we use the Law of Sines
::让我们来讨论一下几个问题在那里我们使用Sines定律

1. Find $\begin{aligned} ∠ B \end{aligned}$ .
::1. 查找B.

Use the Law of Sines to determine the angle.
::使用Sines法则来确定角度。

$\begin{aligned} \frac{\sin 41}{12} & = \frac{\sin B}{23} \\ 23 \sin 41 & = 12 \sin B \\ \frac{23 \sin 41}{12} & = \sin B \\ 1.257446472 & = \sin B \end{aligned}$

::-=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

Since no angle exists with a sine greater than 1, there is no solution to this problem.
::由于没有任何角度存在超过1的必备条件,因此这个问题没有解决办法。

We also could have compared $\begin{aligned} a \end{aligned}$ and $\begin{aligned} b \sin A \end{aligned}$ beforehand to see how many solutions there were to this triangle.
::我们还可以事先比较一个和BsinA 来了解这个三角形有多少解决办法。

$\begin{aligned} a = 12, b \sin A = 15.1 \end{aligned}$ : since $\begin{aligned} 12 < 15.1, a < b \sin A \end{aligned}$ which tells us there are no solutions.
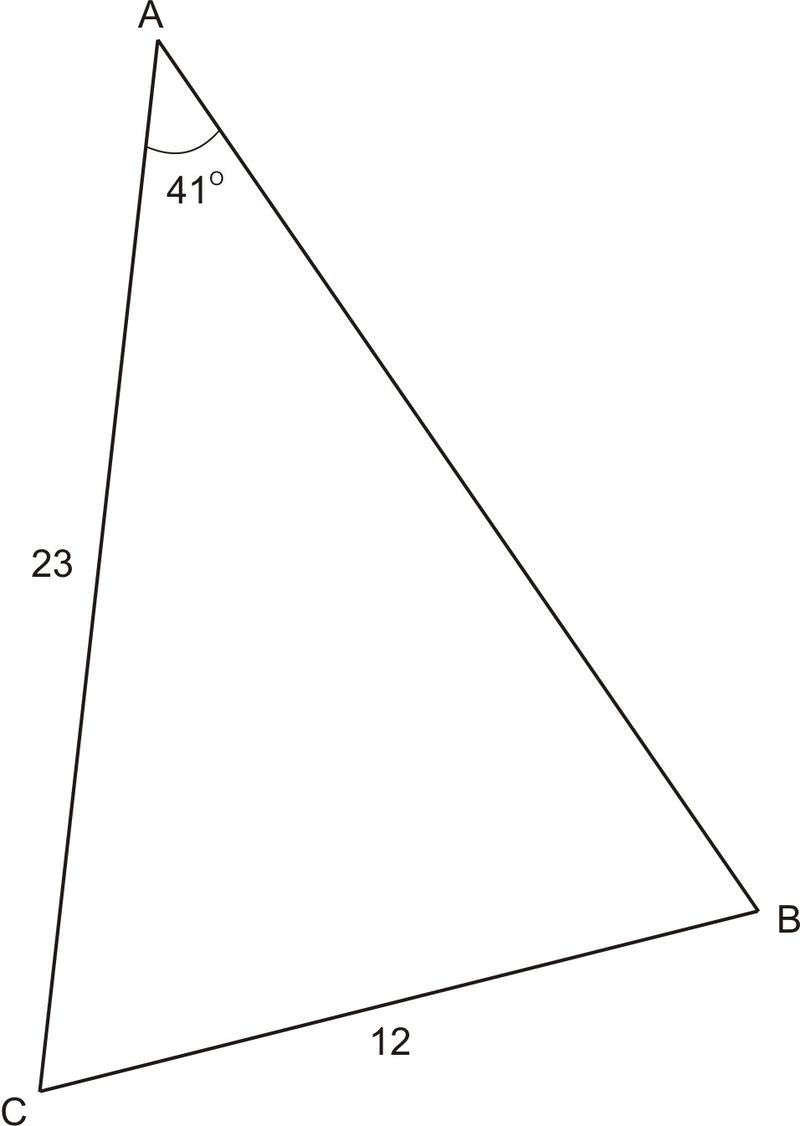
::a=12,bsinA=15.1:自12<15.1,a<bsinA 告诉我们没有解决办法。

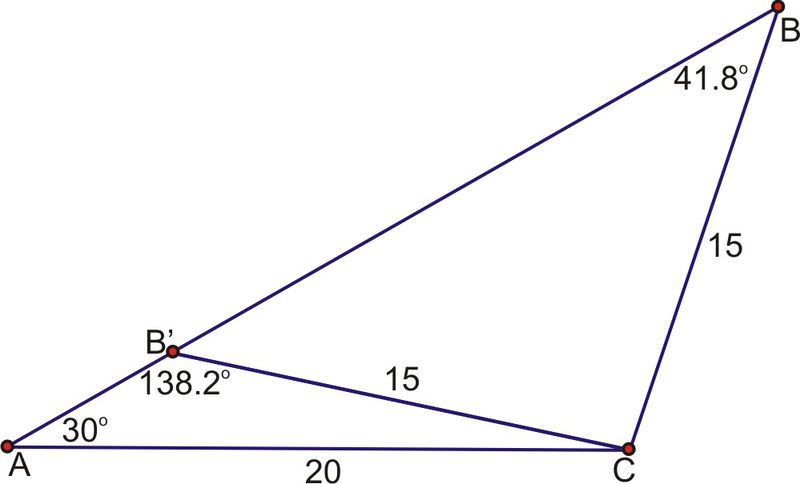
2. In $\begin{aligned} △ A B C, a = 15, b = 20 \end{aligned}$ , and $\begin{aligned} ∠ A = 30^{\circ} \end{aligned}$ . Find $\begin{aligned} ∠ B \end{aligned}$ .
::2. 在“ABC,a=15,b=20”和“A=30”。请查找“B”。

Again in this case, $\begin{aligned} a < b \end{aligned}$ and we know two sides and a non-included angle. By comparing $\begin{aligned} a \end{aligned}$ and $\begin{aligned} b \sin A \end{aligned}$ , we find that $\begin{aligned} a = 15, b \sin A = 10 \end{aligned}$ . Since $\begin{aligned} 15 > 10 \end{aligned}$ we know that there will be two solutions to this problem.
::在此情况下, a <b 和我们知道两面和一个未包含的角度。通过比较 a 和 bsina, 我们发现 a= 15, bsinA=10。因为15> 10 我们知道这个问题有两种解决办法。

$\begin{aligned} \frac{\sin 30}{15} & = \frac{\sin B}{20} \\ 20 \sin 30 & = 15 \sin B \\ \frac{20 \sin 30}{15} & = \sin B \\ 0.6666667 & = \sin B \\ ∠ B & = {41.8}^{\circ} \end{aligned}$

::-========================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

There are two angles less than $\begin{aligned} 180^{\circ} \end{aligned}$ with a sine of 0.6666667, however. We found the first one, $\begin{aligned} {41.8}^{\circ} \end{aligned}$ , by using the inverse sine function. To find the second one, we will subtract $\begin{aligned} {41.8}^{\circ} \end{aligned}$ from $\begin{aligned} 180^{\circ}, ∠ B = 180^{\circ} - {41.8}^{\circ} = {138.2}^{\circ} \end{aligned}$ .
::不过,有两个小于180的角,正弦为0.666667。我们通过使用逆正弦函数发现了第一个角,即41.8。要找到第二个角,我们将从180,B=18041.841.8138.2中减去41.8。

To check to make sure $\begin{aligned} {138.2}^{\circ} \end{aligned}$ is a solution, we will use the Triangle Sum Theorem to find the third angle. Remember that all three angles must add up to $\begin{aligned} 180^{\circ} \end{aligned}$ .
::要检查以确保138.2是一个解决方案, 我们将会使用三角 Sum 理论来找到第三个角度。记住所有三个角度必须加到 180 。

$\begin{aligned} 180^{\circ} - (30^{\circ} + {41.8}^{\circ}) = {108.2}^{\circ} & or & 180^{\circ} - (30^{\circ} + {138.2}^{\circ}) = {11.8}^{\circ} \end{aligned}$

::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}

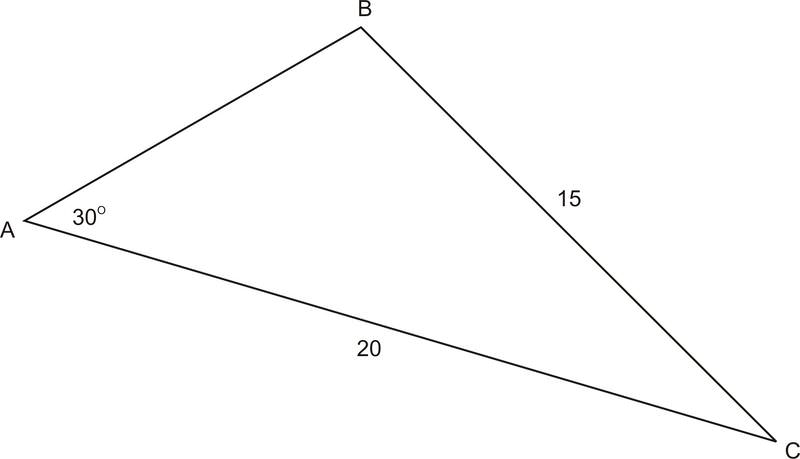
This problem yields two solutions. Either $\begin{aligned} ∠ B = {41.8}^{\circ} \end{aligned}$ or $\begin{aligned} {138.2}^{\circ} \end{aligned}$ .
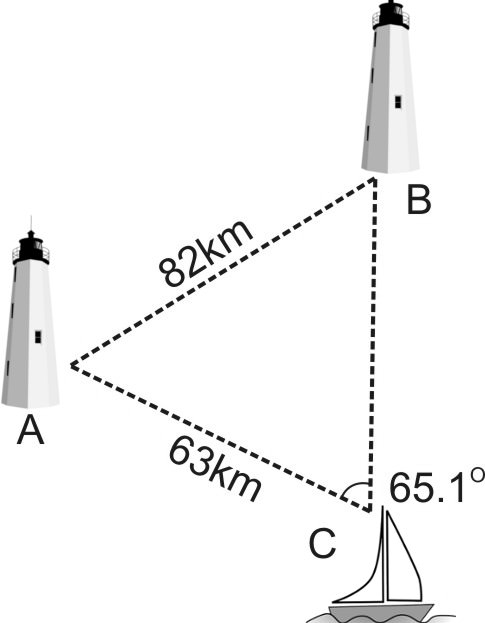
::这个问题产生两种解决办法,要么是B=41.8,要么是138.2。

3. A boat leaves lighthouse $\begin{aligned} A \end{aligned}$ and travels 63km. It is spotted from lighthouse $\begin{aligned} B \end{aligned}$ , which is 82km away from lighthouse $\begin{aligned} A \end{aligned}$ . The boat forms an angle of $\begin{aligned} {65.1}^{\circ} \end{aligned}$ with both lighthouses. How far is the boat from lighthouse $\begin{aligned} B \end{aligned}$ ?
::3. 一艘船离开灯塔A,旅行63公里。从离灯塔A82公里处的灯塔B可以看到该船。该船与两座灯塔的距离为65.1英寸。船离灯塔B有多远?

In this problem, we again have the SSA angle case. In order to find the distance from the boat to the lighthouse (a) we will first need to find the measure of $\begin{aligned} ∠ A \end{aligned}$ . In order to find $\begin{aligned} ∠ A \end{aligned}$ , we must first use the Law of Sines to find $\begin{aligned} ∠ B \end{aligned}$ . Since $\begin{aligned} c > b \end{aligned}$ , this situation will yield exactly one answer for the measure of $\begin{aligned} ∠ B \end{aligned}$ .
::在这个问题上,我们又有了SSA角度案例。为了找到从船到灯塔的距离(a) 我们首先需要找到QA。为了找到QA。为了找到QA,我们首先必须使用Sines法律来找到QB。由于c>b,这种情况将产生一个精确的答案,以达到QB。

$\begin{aligned} \frac{\sin {65.1}^{\circ}}{82} & = \frac{\sin B}{63} \\ \frac{63 \sin {65.1}^{\circ}}{82} & = \sin B \\ 0.6969 & \approx \sin B \\ ∠ B & = {44.2}^{\circ} \end{aligned}$

::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:

Now that we know the measure of $\begin{aligned} ∠ B \end{aligned}$ , we can find the measure of angle $\begin{aligned} A, ∠ A = 180^{\circ} - {65.1}^{\circ} - {44.2}^{\circ} = {70.7}^{\circ} \end{aligned}$ . Finally, we can use $\begin{aligned} ∠ A \end{aligned}$ to find side $\begin{aligned} a \end{aligned}$ .
::现在我们知道QB的度量了, 我们可以找到角度A的度量, A=18065.144.270.7。最后, 我们可以用QA找到侧A 。

$\begin{aligned} \frac{\sin {65.1}^{\circ}}{82} & = \frac{\sin {70.7}^{\circ}}{a} \\ \frac{82 \sin {70.7}^{\circ}}{\sin {65.1}^{\circ}} & = a \\ a & = 85.3 \end{aligned}$

::65.1

The boat is approximately 85.3 km away from lighthouse $\begin{aligned} B \end{aligned}$ .
::该船离灯塔B大约85.3公里。

Examples
::实例

Example 1
::例1

Earlier, you were asked to use your knowledge of math to draw a piece of glass for a sculpture.
::早些时候,你被要求使用你的数学知识为雕塑绘制一块玻璃

A drawing of this situation looks like this:
::情况看起来是这样的:

You can start by using the Law of Sines:
::您可以首先使用Sines法则:

$\begin{aligned} \frac{\sin A}{a} = \frac{\sin B}{b} \end{aligned}$
::Aa=sinBb 性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、性别、

and substitute known values:
::替换已知值:

$\begin{aligned} \frac{\sin 35}{14} = \frac{\sin B}{17} \end{aligned}$
::3514=sin_B17 时间轴: 3514=sin_B17

Then solving for $\begin{aligned} \sin B \end{aligned}$ :
::然后解决罪的B:

$\begin{aligned} \sin B = \frac{17 \sin 35^{\circ}}{14} \end{aligned}$
::B=17sin =35}=14

And so
::如此,这样

$\begin{aligned} B \approx {44.15}^{\circ} \end{aligned}$
::B44.15______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Since the interior angles of any triangle add up to $\begin{aligned} 180^{\circ} \end{aligned}$ , we can find $\begin{aligned} ∠ C \end{aligned}$ :
::因为任何三角形的内部角度加起来等于180,

$\begin{aligned} C = 180^{\circ} - 35^{\circ} - {44.15}^{\circ} \\ C = 100.85 \end{aligned}$

::C=180,35,44,15,C=100,85

This information can be used again in the Law of Sines:
::这些资料可再次用于《锡纳法》:

$\begin{aligned} \frac{\sin A}{a} = \frac{\sin C}{c} \\ \frac{\sin 35}{14} = \frac{\sin 100.86}{c} \\ c = \frac{14 \sin 100.86}{\sin 35} \\ c = \frac{13.75}{.5735} \\ c = 23.976 \end{aligned}$

::-====================================================================================================================================================================================================================================================================23===================================================================================================================================

Example 2
::例2

Prove using the Law of Sines: $\begin{aligned} \frac{a - c}{c} = \frac{\sin A - \sin C}{\sin C} \end{aligned}$
::使用Sines法证明: a-cc=sinA-sinC

$\begin{aligned} \frac{\sin A}{a} & = \frac{\sin C}{c} \\ c \sin A & = a \sin C \\ c \sin A - c \sin C & = a \sin C - c \sin C \\ c (\sin A - \sin C) & = \sin C (a - c) \\ \frac{\sin A - \sin C}{\sin C} & = \frac{a - c}{c} \end{aligned}$

:a-c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-(c)-

Example 3
::例3

Find all possible measures of angle $\begin{aligned} B \end{aligned}$ if any exist for the following triangle values: $\begin{aligned} A = {32.5}^{\circ}, a = 26, b = 37 \end{aligned}$
::如果对以下三角值存在的话, 查找角 B 的所有可能的度量 : A= 32.5 , a= 26, b= 37

$\begin{aligned} \frac{\sin {32.5}^{\circ}}{26} = \frac{\sin B}{37} \to B = {49.9}^{\circ} \end{aligned}$ or $\begin{aligned} 180^{\circ} - {49.9}^{\circ} = {130.1}^{\circ} \end{aligned}$
::或 180\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\B37B=49.9\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Example 4
::例4

Find all possible measures of angle $\begin{aligned} B \end{aligned}$ if any exist for the following triangle values: $\begin{aligned} A = {42.3}^{\circ}, a = 16, b = 26 \end{aligned}$
::如果对下列三角值存在的话,请查找角B的所有可能的测量尺度:A=42.3,a=16,b=26

no solution
::无解决方案

Review
::回顾

Find all possible measures of angle $\begin{aligned} B \end{aligned}$ if any exist for each of the following triangle values.
::如果对以下三角值中的每一值都存在,请查找角B的所有可能的度量。

$\begin{aligned} A = 30^{\circ}, a = 13, b = 15 \end{aligned}$
::A=30,a=13,b=15

$\begin{aligned} A = 42^{\circ}, a = 21, b = 12 \end{aligned}$
::A=42,a=21,b=12

$\begin{aligned} A = 22^{\circ}, a = 36, b = 37 \end{aligned}$
::A=22,a=36,b=37

$\begin{aligned} A = 87^{\circ}, a = 14, b = 12 \end{aligned}$
::A=87,a=14,b=12

$\begin{aligned} A = 31^{\circ}, a = 25, b = 44 \end{aligned}$
::A=31,a=25,b=44

$\begin{aligned} A = 59^{\circ}, a = 37, b = 41 \end{aligned}$
::A=59,a=37,b=41

$\begin{aligned} A = 81^{\circ}, a = 22, b = 20 \end{aligned}$
::A=81,a=22,b=20

$\begin{aligned} A = 95^{\circ}, a = 31, b = 34 \end{aligned}$
::A=95,a=31,b=34

$\begin{aligned} A = 112^{\circ}, a = 12, b = 15 \end{aligned}$
::A=112,a=12,b=15

$\begin{aligned} A = 78^{\circ}, a = 20, b = 16 \end{aligned}$
::A=78,a=20,b=16

In $\begin{aligned} △ A B C \end{aligned}$ , a=10 and $\begin{aligned} m ∠ B = 39^{\circ} \end{aligned}$ . What's a possible value for b that would produce two triangles?
::在“ABC”中, a=10 和 mB=39\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\B\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

In $\begin{aligned} △ A B C \end{aligned}$ , a=15 and $\begin{aligned} m ∠ B = 67^{\circ} \end{aligned}$ . What's a possible value for b that would produce no triangles?
::在 ABC 中, a= 15 和 mB= 67\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ xB\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\B\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\BBBBBBB

In $\begin{aligned} △ A B C \end{aligned}$ , a=21 and $\begin{aligned} m ∠ B = 99^{\circ} \end{aligned}$ . What's a possible value for b that would produce one triangle?
::在 ABC 中, a= 21 和 mB= 99\\\\\\\\\\\\\\\\\\\\\\\\可以产生一个三角形的 b 值是多少?

Bill and Connie are each leaving for school. Connie's house is 4 miles due east of Bill's house. Bill can see the school in the direction $\begin{aligned} 40^{\circ} \end{aligned}$ east of north. Connie can see the school on a line $\begin{aligned} 51^{\circ} \end{aligned}$ west of north. What is the straight line distance of each person from the school?
::比尔和康妮都要去上学康妮的房子在比尔房子东面4英里处

Rochelle and Rose are each looking at a hot air balloon. They are standing 2 miles apart. The angle of elevation for Rochelle is $\begin{aligned} 30^{\circ} \end{aligned}$ and the angle of elevation for Rose is $\begin{aligned} 34^{\circ} \end{aligned}$ . How high off the ground is the balloon?
::Rochelle和Rose都看着热气球,它们相距两英里。 Rochelle的高度角是30°C,Rose的高度角是34°C。气球离地面有多高?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

Sines法律

Law of Sines ::Sines法律

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Law of Sines
::Sines法律

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)