Course: 5.11 科士法 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 科士法

Collapse Expand
科士法
While helping your mom bake one day, the two of you get an unusual idea. You want to cut the cake into pieces, and then frost over the surface of each piece. You start by cutting out a slice of the cake, but you don't quite cut the slice correctly. It ends up being an oblique triangle , with a 5 inch side, a 6 inch side, and an angle of $\begin{aligned} 70^{\circ} \end{aligned}$ between the sides you measured. Can you help your mom determine the length of the third side, so she can figure out how much frosting to put out?
::在帮助你妈妈做饭的某一天, 你们两个得到一个不同寻常的想法。你想把蛋糕切成碎片, 然后在每块表面结霜。您先切出一块蛋糕, 但是您没有完全正确切开切片。最后它变成了一个斜形三角形, 侧面为5英寸, 侧面为6英寸, 侧面为70英寸。您可以帮助你妈妈确定第三边的长度, 这样她就能弄清楚要喷出多少糖霜吗 ?

Law of Cosines
::科士法

The is a fantastic extension of the to oblique triangles. In this section, we show some interesting ways to utilize this formula to analyze real world situations.
::这是对斜三角形的惊人延伸。在本节中,我们展示了一些有趣的方法来利用这个公式来分析真实的世界局势。

Let's take a look at a few problems where we use the Law of Cosines.
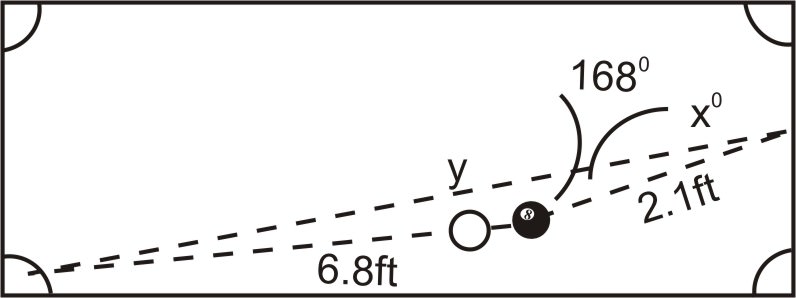
::让我们来看看几个问题我们使用科辛斯定律。

1. In a game of pool, a player must put the eight ball into the bottom left pocket of the table. Currently, the eight ball is 6.8 feet away from the bottom left pocket. However, due to the position of the cue ball, she must bank the shot off of the right side bumper. If the eight ball is 2.1 feet away from the spot on the bumper she needs to hit and forms a $\begin{aligned} 168^{\circ} \end{aligned}$ angle with the pocket and the spot on the bumper, at what angle does the ball need to leave the bumper?
::1. 在游泳池游戏中,玩家必须把8个球放入桌子的左下角口袋,目前,8个球离左下角6.8英尺,然而,由于球的位置,她必须把右侧保险杠的射击打下来,如果8个球离保险杠的点2.1英尺远,她需要用口袋和保险杠上的点子打到168角,球需要从哪个角度离开保险杠?

Note: This is actually a trick shot performed by spinning the eight ball, and the eight ball will not actually travel in straight-line trajectories. However, to simplify the problem, assume that it travels in straight lines.
::注意 : 这实际上是通过旋转 8 球所执行的魔术射击, 而 8 球将不实际在直线轨道中运行。但是, 为了简化问题, 假设它沿直线运行。

In the scenario above, we have the SAS case, which means that we need to use the Law of Cosines to begin solving this problem. The Law of Cosines will allow us to find the distance from the spot on the bumper to the pocket "> $\begin{aligned} (y) \end{aligned}$ . Once we know $\begin{aligned} y \end{aligned}$ , we can use the to find the angle $\begin{aligned} (X) \end{aligned}$ .
::在以上情况下,我们有SAS案例,这意味着我们需要使用Casines法来开始解决这个问题。 Cosines法将允许我们找到从保险杠上到口袋的距离。一旦我们知道 y,我们就可以用它来找到角度(X ) 。

$\begin{aligned} y^{2} & = {6.8}^{2} + {2.1}^{2} - 2 (6.8) (2.1) \cos 168^{\circ} \\ y^{2} & = 78.59 \\ y & = 8.86 f e e t \end{aligned}$

::y2=78.59y=8.86英尺 y2=78.59y=8.86英尺

2. The distance from the spot on the bumper to the pocket is 8.86 feet. We can now use this distance and the Law of Sines to find angle $\begin{aligned} X \end{aligned}$ . Since we are finding an angle, we are faced with the SSA case, which means we could have no solution, one solution, or two solutions. However, since we know all three sides this problem will yield only one solution.
::2. 从保险杠上到口袋的距离为8.86英尺,我们现在可以利用这条距离和辛那斯定律寻找角度X。由于我们找到一个角度,我们面临特别敏感区的情况,这意味着我们不可能有解决办法、一个解决办法或两个解决办法,然而,由于我们知道所有三个方面,这个问题只能产生一个解决办法。

$\begin{aligned} \frac{\sin 168^{\circ}}{8.86} & = \frac{\sin X}{6.8} \\ \frac{6.8 \sin 168^{\circ}}{8.86} & = \sin X \\ 0.1596 & \approx \sin B \\ ∠ B & = {8.77}^{\circ} \end{aligned}$

::188.86=sinX6.86.8sin1688.86=sinX0.1596B=8.77

In the previous example, we looked at how we can use the Law of Sines and the Law of Cosines together to solve a problem involving the SSA case. In this section, we will look at situations where we can use not only the Law of Sines and the Law of Cosines, but also the Pythagorean Theorem and trigonometric ratios. We will also look at another real-world application involving the SSA case.
::在前一例中,我们研究了我们如何能够共同使用《辛那斯法》和《科辛斯法》来解决涉及特别敏感区案件的问题。在本节中,我们将审视我们不仅可以使用辛那斯法和科辛斯法的情况,而且可以使用毕达哥伦理论和三角比的情况。我们还将审视涉及特别敏感区案件的另一个现实应用情况。

3. Three scientists are out setting up equipment to gather data on a local mountain. Person 1 is 131.5 yards away from Person 2, who is 67.8 yards away from Person 3. Person 1 is 72.6 yards away from the mountain. The mountains forms a $\begin{aligned} 103^{\circ} \end{aligned}$ angle with Person 1 and Person 3, while Person 2 forms a $\begin{aligned} {92.7}^{\circ} \end{aligned}$ angle with Person 1 and Person 3. Find the angle formed by Person 3 with Person 1 and the mountain.
::3. 三名科学家正在建立收集当地山地数据的设备。人1距离人2131.5码,距离人267.8码。人1离人62.6码。人1离人山72.6码。人1与人1和人3形成103角,人2与人1和人3形成92.7角。人3与人1和人3形成角。

In the triangle formed by the three people, we know two sides and the included angle (SAS). We can use the Law of Cosines to find the remaining side of this triangle, which we will call $\begin{aligned} x \end{aligned}$ . Once we know $\begin{aligned} x \end{aligned}$ , we will two sides and the non-included angle (SSA) in the triangle formed by Person 1, Person 2, and the mountain. We will then be able to use the Law of Sines to calculate the angle formed by Person 3 with Person 1 and the mountain, which we will refer to as $\begin{aligned} Y \end{aligned}$ .
::在三人组成的三角形中,我们知道两面和包括的角度(SAS)。我们可以使用Cisines法则找到这个三角形的剩余面,我们称之为x。一旦我们知道x,我们将在人1、人2和山组成的三角形中找到两面和非包括的角度(SSA)。然后,我们将能够使用Sines法则来计算人3与人1和山形成的角度,我们将称之为Y。

To find $\begin{aligned} x \end{aligned}$ :
::要查找 x:

$\begin{aligned} x^{2} & = {131.5}^{2} + {67.8}^{2} - 2 (131.5) (67.8) \cos 92.7 \\ x^{2} & = 22729.06397 \\ x & = 150.8 y d s \end{aligned}$

::x2=131.52+67.82-2-11.5(67.8)cos92.7x2=22729.06397x=150.8Yds

Now that we know $\begin{aligned} x = 150.8 \end{aligned}$ , we can use the Law of Sines to find $\begin{aligned} Y \end{aligned}$ . Since this is the SSA case, we need to check to see if we will have no solution, one solution, or two solutions. Since $\begin{aligned} 150.8 > 72.6 \end{aligned}$ , we know that we will have only one solution to this problem.
::既然我们知道x=150.8,我们可以使用辛那斯定律来找到Y。由于这是特别敏感区的情况,我们需要检查我们是否没有解决办法、一个解决办法或两个解决办法。自从150.8>72.6以来,我们知道我们只有一种办法解决这个问题。

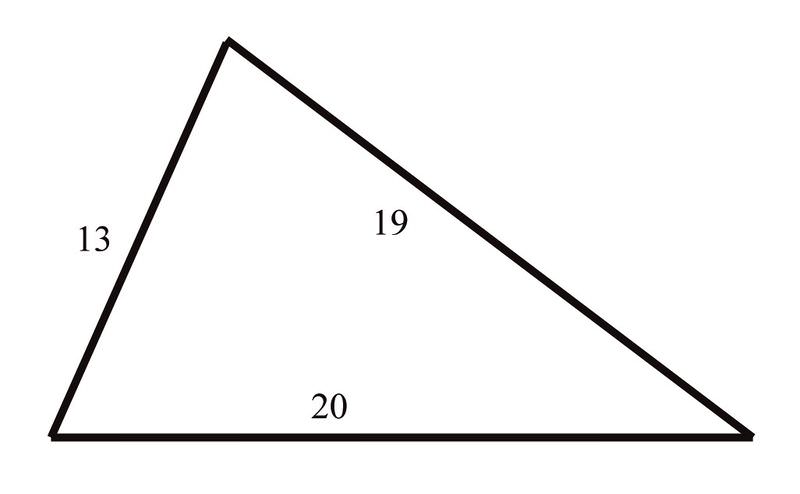
$\begin{aligned} \frac{\sin 103}{150.8} & = \frac{\sin Y}{72.6} \\ \frac{72.6 \sin 103}{150.8} & = \sin Y \\ 0.4690932805 & = \sin Y \\ 28.0 & \approx ∠ Y \end{aligned}$

::103150.8=sinY72.62.6sin103150.8=sinY0.4690932805=sinY2.80.Y

4. Katie is constructing a kite shaped like a triangle.
::4. 凯蒂正在建造一个三角形的风筝。

She knows that the lengths of the sides are a = 13 inches, b = 20 inches, and c = 19 inches. What is the measure of the angle between sides "a" and "b"?
::她知道两边的长度是 a = 13 英寸, b = 20 英寸, c = 19 英寸。 A 和 B 之间的角是多少?

Since she knows the length of each of the sides of the triangle, she can use the Law of Cosines to find the angle desired:
::既然她知道三角形每一边的长度, 她可以使用科辛斯定律来找到理想的角度:

$\begin{aligned} c^{2} & = a^{2} + b^{2} - 2 (a) (b) \cos C \\ 19^{2} & = 13^{2} + 20^{2} - (2) (13) (20) \cos C \\ 361 & = 169 + 400 - 520 \cos C \\ - 208 & = - 520 \cos C \\ \cos C & = 0.4 \\ C \approx {66.42}^{\circ} \end{aligned}$

::c2=a2+b2-2(a)(b)cosC192=132+202-(2)(13)(20cosC361=169+400-520cC-208=520cosCosCosC=0.4C66.42

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine the length of the third side.
::早些时候,有人要求你确定第三边的长度。

You can use the Law of Cosines to help your mom find out the length of the third side on the piece of cake:
::你可以用《科辛斯定律》来帮助你妈妈找出蛋糕上第三边的长度

$\begin{aligned} c^{2} = a^{2} + b^{2} - 2 a b \cos C \\ c^{2} = 5^{2} + 6^{2} + (2) (5) (6) \cos 70^{\circ} \\ c^{2} = 25 + 36 + 60 (.342) \\ c^{2} = 81.52 \\ c \approx 9.03 \end{aligned}$

::c2=a2+b2-2abcosc2=52+62+(2)(6)(6)cos70c2=25+36+60(3.442)c2=81.52c9.03

The piece of cake is just a little over 9 inches long.
::蛋糕只长了9英寸多一点

Example 2
::例2

You are cutting a triangle out for school that looks like this:
::你为学校切开三角形看起来像这样:

Find side $\begin{aligned} c \end{aligned}$ (which is the side opposite the $\begin{aligned} 14^{\circ} \end{aligned}$ angle) and $\begin{aligned} ∠ B \end{aligned}$ (which is the angle opposite the side that has a length of 14).
::查找 c 和和和和和 B 的边( 是 14 的边对面的角 ) ( 是 14 长 14 的边对面的角 ) 。

You know that two of the sides have lengths of 11 and 14 inches, and that the angle between them is $\begin{aligned} 14^{\circ} \end{aligned}$ . You can use this to find the length of the third side:
::你知道两边的长度是11和14英寸, 它们之间的角是14英寸。您可以用这个来找到第三边的长度 :

$\begin{aligned} c^{2} = a^{2} + b^{2} - 2 a b \cos θ \\ c^{2} = 121 + 196 - (2) (11) (14) (.97) \\ c^{2} = 121 + 196 - 307.384 \\ c^{2} = 9.16 \\ c = 3.03 \end{aligned}$

::c2=a2+b2-2abc2=121+196-(2)(11) (14) (.97c2=121+196-307.384c2=9.16c=3.03)

And with this you can use the Law of Sines to solve for the unknown angle:
::用这个你可以用辛那定律解决未知角度的问题:

$\begin{aligned} \frac{\sin 14^{\circ}}{3.03} = \frac{\sin B}{11} \\ \sin B = \frac{11 \sin 14^{\circ}}{3.03} \\ \sin B = .878 \\ B = \sin^{- 1} (.0307) = {61.43}^{\circ} \end{aligned}$

::143.03=sinB11sinB=11sin143.03sinB=878B=sin-1(.0307)=61.43

Example 3
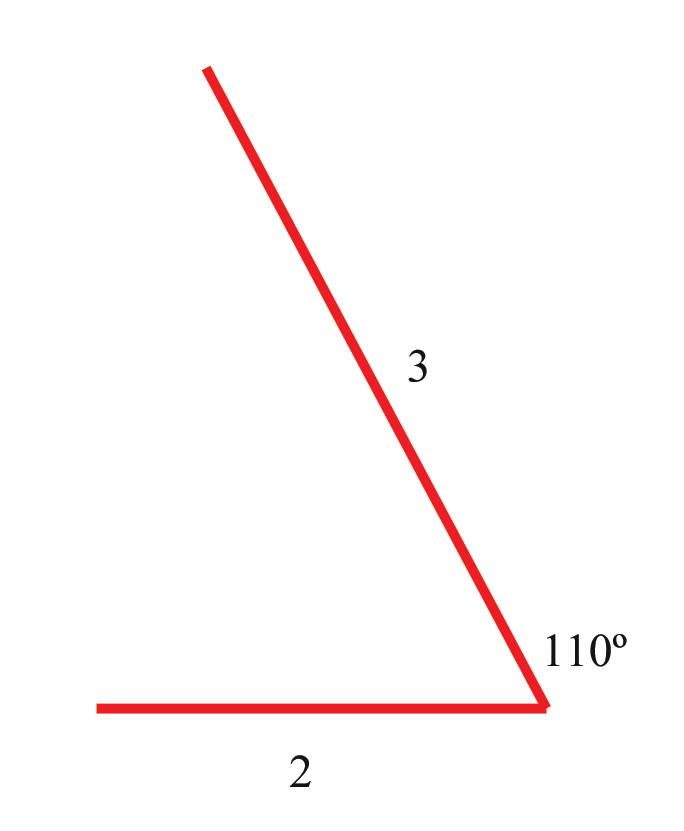
::例3

While hiking one day you walk for 2 miles in one direction. You then turn $\begin{aligned} 110^{\circ} \end{aligned}$ to the left and walk for 3 more miles. Your path looks like this:
::在徒步旅行的一天,你向一个方向走2英里。然后左转110英里,再行走3英里。你的路径是这样的:

When you turn to the left again to complete the triangle that is your hiking path for the day, how far will you have to walk to complete the third side? What angle should you turn before you start walking back home?
::当您再次向左翻转以完成您一天的徒步路线的三角形时, 您需要走多远才能完成第三边? 在您开始走回家之前, 您应该从哪个角度转弯 ?

Since you know the lengths of two of the legs of the triangle, along with the angle between them, you can use the Law of Cosines to find out how far you'll have to walk along the third leg:
::既然你知道三角形两条腿的长度以及两条三角形之间的角你可以用《科辛斯定律》

$\begin{aligned} c^{2} = a^{2} + b^{2} + 2 a b \cos 70^{\circ} \\ c^{2} = 4 + 1 + (2) (2) (1) (.342) \\ c^{2} = 6.368 \\ c = \sqrt{6.368} \approx 2.52 \end{aligned}$

::c2=a2+b2+2abcos @70*c2=4+1+(2)(1)(342)c2=6.368c=6.3682.52

Now you have enough information to solve for the interior angle of the triangle that is supplementary to the angle you need to turn:
::现在您有足够的信息可以解答三角形的内部角, 该三角形是您需要翻转角的补充 :

$\begin{aligned} \frac{\sin A}{a} = \frac{\sin B}{b} \\ \frac{\sin 70^{\circ}}{2.52} = \frac{\sin B}{2} \\ \sin B = \frac{2 \sin 70^{\circ}}{2.52} = \frac{1.879}{2.52} = .746 \\ B = \sin^{- 1} (.746) = {48.25}^{\circ} \end{aligned}$

::-========================================================================================================================================================================================48.25===================================================================================================================================================================================================================================================================================================================================

The angle $\begin{aligned} {48.25}^{\circ} \end{aligned}$ is the interior angle of the triangle. So you should turn $\begin{aligned} 90^{\circ} + (90^{\circ} - {48.25}^{\circ}) = 90^{\circ} + {41.75}^{\circ} = {131.75}^{\circ} \end{aligned}$ to the left before starting home.
::角度 48.25 是三角形的内部角。所以您在开始返回前应该向左转90( 9048.25) =9041. 75131.75。

Example 4
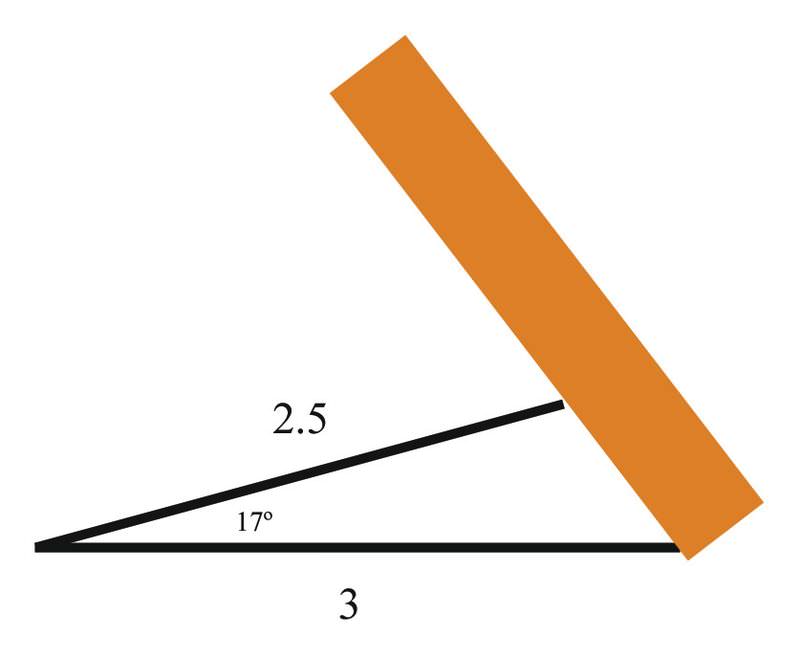
::例4

A support at a construction site is being used to hold up a board so that it makes a triangle, like this:
::建筑工地的支持被用来支撑一个板子这样它就能形成一个三角形,像这样:

If the angle between the support and the ground is $\begin{aligned} 17^{\circ} \end{aligned}$ , the length of the support is 2.5 meters, and the distance between where the board touches the ground and the bottom of the support is 3 meters, how far along the board is the support touching? What is the angle between the board and the ground?
::如果支持与地面之间的角是 17 ,支持的长度是 2.5米, 而板与支持底部之间的距离是 3米, 支持与地面之间的距离是多少? 支持与地面之间的角是多少?

You should use the Law of Cosines first to solve for the distance from the ground to where the support meets the board:
::您应该首先使用Casines定律来解决支持与董事会的距离问题:

$\begin{aligned} c^{2} = a^{2} + b^{2} + 2 a b \cos 17^{\circ} \\ c^{2} = 6.25 + 9 + (2) (2.5) (3) \cos 17^{\circ} \\ c^{2} = 6.25 + 9 + (2) (2.5) (3) (.956) \\ c^{2} = 26.722 \\ c \approx 5.17 \end{aligned}$

::C2=a2+b2+2abcos17c2=6.25+9+(2)(2.5)(3)cs17c2=6.25+9+(2)(2.5)(3)(3)(956)c2=26.722c5.17

And now you can use the Law of Sines:
::现在你可以使用辛尼定律了:

$\begin{aligned} \frac{\sin A}{a} = \frac{\sin B}{b} \\ \frac{\sin 17^{\circ}}{5.17} = \frac{\sin B}{2.5} \\ \sin B = \frac{2.5 \sin 17^{\circ}}{5.17} = .1414 \\ B = \sin^{- 1} (.1414) = {8.129}^{\circ} \end{aligned}$

::-=====================================================================================================================================================================================8.

Review
::回顾

In $\begin{aligned} △ A B C \end{aligned}$ , a=12, b=15, and c=20.
::在 ABC 中, a=12, b=15, c=20。

Find $\begin{aligned} m ∠ A \end{aligned}$ .
::找妈妈吧

Find $\begin{aligned} m ∠ B \end{aligned}$ .
::去找MB

Find $\begin{aligned} m ∠ C \end{aligned}$ .
::寻找 mC。

In $\begin{aligned} △ D E F \end{aligned}$ , d=25, e=13, and f=16.
::在“DEF, d=25, e=13, f=16”中。

Find $\begin{aligned} m ∠ D \end{aligned}$ .
::去找MD

Find $\begin{aligned} m ∠ E \end{aligned}$ .
::去找妈妈

Find $\begin{aligned} m ∠ F \end{aligned}$ .
::去找MF

In $\begin{aligned} △ K B P \end{aligned}$ , k=19, $\begin{aligned} ∠ B = 61^{\circ} \end{aligned}$ , and p=12.
::KBP,k=19,B=61,p=12。

Find the length of b.
::查找 b 的长度。

Find $\begin{aligned} m ∠ K \end{aligned}$ .
::去找妈妈

Find $\begin{aligned} m ∠ P \end{aligned}$ .
::寻找 mP。

While hiking one day you walk for 5 miles due east, then turn to the left and walk 3 more miles $\begin{aligned} 30^{\circ} \end{aligned}$ west of north. At this point you want to return home. How far are you from home if you were to walk in a straight line?
::有一天,你徒步往东走5英里,然后向左转,再往北走3英里30英里。此时,你想要回家。如果你走一条直线,你离家多远?

A parallelogram has sides of 20 and 31 ft, and an angle of $\begin{aligned} 46^{\circ} \end{aligned}$ . Find the length of the longer diagonal of the parallelogram.
::平行图的侧面为 20 和 31 英尺,角度为 46 。查找平行图的长对角长度。

Dirk wants to find the length of a long building from one side (point A) to the other (point B). He stands outside of the building (at point C), where he is 500 ft from point A and 220 ft from point B. The angle at C is $\begin{aligned} 94^{\circ} \end{aligned}$ . Find the length of the building.
::德克希望从一面(A点)到另一面(B点)找到长建筑物的长度。他站在大楼外(C点),从A点起为500英尺,从B点起为220英尺。C点为94英尺。找到大楼的长度。

Determine whether or not each triangle is possible.
::确定每个三角形是否都可能。

a=12, b=15, c=10
::a=12, b=15, c=10

a=1, b=5, c=4
::a=1,b=5,c=4

$\begin{aligned} ∠ A = 32^{\circ} \end{aligned}$ , a=8, b=10
::A=32, a=8, b=10

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

科士法

Law of Cosines ::科士法

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Law of Cosines
::科士法

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)