Course: 5.12 三角通用解决方案

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

三角通用解决方案

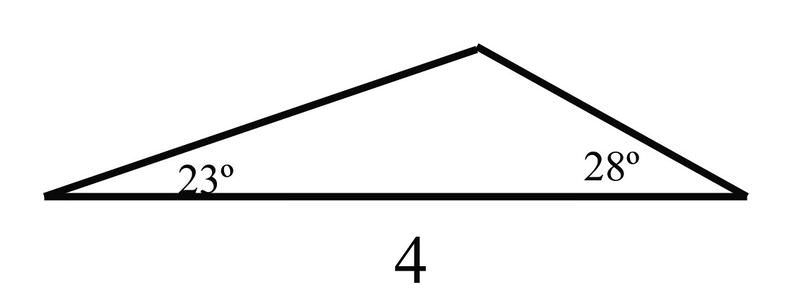
While talking with your little sister one day, the conversation turns to shapes. Your sister is only in junior high school, so while she knows some things about right triangles, such as the , she doesn't know anything about other types of triangles. You show her an example of an oblique triangle by drawing this on a piece of paper:
::有一天,你和你妹妹交谈时,谈话就变成形形色色的。你妹妹只上初中,所以虽然她了解一些右三角,比如右三角,但她对其他三角形一无所知。你用一张纸来给她展示一个斜三角形的例子:

Fascinated, she tells you that she knows how to calculate the area of a triangle using the familiar formula $\begin{aligned} \frac{1}{2} b h \end{aligned}$ and the lengths of sides if the triangle is a right triangle, but that she can't use the formulas on the triangle you just drew.
::她告诉你,她知道如何使用熟悉的公式12bh 来计算三角形的面积,如果三角形是右三角形,则边边的长度,但是她不能在您刚刚绘制的三角形上使用公式。

"Do you know how to find the lengths of sides of the triangle and the area?" she asks.
::“你知道如何找到三角形和区域两边的长度吗?”她问道:

Finding Solutions for Triangles
::为三角寻找解决方案

Finding the sides, angles, and area for right triangles is often learned in Algebra and/or Geometry. However, it is common to learn how to determine this information in non-right triangles in Trigonometry.
::在代数和(或)几何中往往会发现右三角的边、角和区域。然而,在三角测量的非右三角中,通常会学会如何确定这些信息。

Below is a chart summarizing
::下面是一张图表,总结如下:

common
::常见

triangle techniques. This chart describes the type of triangle (either right or oblique), the given information, the appropriate technique to use, and what we can find using each technique.
::三角技术。此图表描述三角形的类型( 右侧或斜角)、给定的信息、合适的使用技术, 以及使用每种技术我们能找到什么。

Type of Triangle:	Given Information:	Technique:	What we can find:
Right	Two sides	Pythagorean Theorem	Third side
Right	One angle and one side	Trigonometric ratios	Either of the other two sides
Right	Two sides	Trigonometric ratios	Either of the other two angles
Oblique	2 angles and a non-included side (AAS)		The other non-included side
Oblique	2 angles and the included side (ASA)	Law of Sines	Either of the non-included sides
Oblique	2 sides and the angle opposite one of those sides (SSA) – Ambiguous case	Law of Sines	The angle opposite the other side (can yield no, one, or two solutions)
Oblique	2 sides and the included angle (SAS)		The third side
Oblique	3 sides	Law of Cosines	Any of the three
			angles

Solving Triangles
::溶解三角形

1. In $\begin{aligned} △ A B C, a = 12, b = 13, c = 8 \end{aligned}$ . Solve the triangle.
::1. ABC,a=12,b=13,c=8. 解决三角形。

Since we are given all three sides in the triangle, we can use the Law of Cosines. Before we can solve the triangle, it is important to know what information we are missing. In this case, we do not know any of the angles, so we are solving for $\begin{aligned} ∠ A, ∠ B \end{aligned}$ , and $\begin{aligned} ∠ C \end{aligned}$ . We will begin by finding $\begin{aligned} ∠ A : \end{aligned}$
::既然三角形的三边都给了我们,我们就可以使用科辛斯定律。在解决三角形之前,重要的是要知道我们缺少了哪些信息。在这种情况下,我们不知道任何角度,所以我们正在解决A,B和C。我们首先要找到A:

\begin{aligned} 12^{2} & = 8^{2} + 13^{2} - 2 (8) (13) \cos A \\ 144 & = 233 - 208 \cos A \\ - 89 & = - 208 \cos A \\ 0.4278846154 & = \cos A \\ 64.7 & \approx ∠ A \end{aligned}

::122=82+132-2(8)(13)cosA144=233-208cosA-89208cos*A.4278846154=cosA.64.7A

Now, we will find $\begin{aligned} ∠ B \end{aligned}$ by using the Law of Cosines. Keep in mind that you can now also use the Law of Sines to find $\begin{aligned} ∠ B \end{aligned}$ . Use whatever method you feel more comfortable with.
::现在,我们将通过使用“科辛定律”来找到“B”。记住,你现在也可以使用“Sine定律”来找到“B”。使用你觉得更舒服的方法。

\begin{aligned} 13^{2} & = 8^{2} + 12^{2} - 2 (8) (12) \cos B \\ 169 & = 208 - 192 \cos B \\ - 39 & = - 192 \cos B \\ 0.2031 & = \cos B \\ {78.3}^{\circ} & \approx ∠ B \end{aligned}

::132=82+122-2(8)(12)cos_B169=208-192cos_B-39_192cos_B_39_192cos_B0.2031=cos_B78.3_B

We can now quickly find $\begin{aligned} ∠ C \end{aligned}$ by using the Triangle Sum Theorem, $\begin{aligned} 180^{\circ} - {64.7}^{\circ} - {78.3}^{\circ} = 37^{\circ} \end{aligned}$
::利用三角理论 18064.778.337

2. In triangle $\begin{aligned} D E F, d = 43, e = 37 \end{aligned}$ , and $\begin{aligned} ∠ F = 124^{\circ} \end{aligned}$ . Solve the triangle.
::2. 在三角DEF,d=43,e=37,和F=124。解决三角。

In this triangle, we have the SAS case because we know two sides and the included angle. This means that we can use the Law of Cosines to solve the triangle. In order to solve this triangle, we need to find side $\begin{aligned} f, ∠ D \end{aligned}$ , and $\begin{aligned} ∠ E \end{aligned}$ . First, we will need to find side $\begin{aligned} f \end{aligned}$ using the Law of Cosines.
::在这个三角形中,我们有SAS案例, 因为我们知道两面和包括的角度。这意味着我们可以使用Cosines定律来解决三角形。为了解决这个三角形, 我们需要找到F, D, 和 E。首先, 我们需要找到使用Cosines定律的侧面。

\begin{aligned} f^{2} & = 43^{2} + 37^{2} - 2 (43) (37) \cos 124 \\ f^{2} & = 4997.351819 \\ f & \approx 70.7 \end{aligned}

::f2=432+372-2(43)(37cos124f2=4997.351819f_70.7)

Now that we know $\begin{aligned} f \end{aligned}$ , we know all three sides of the triangle. This means that we can use the Law of Cosines to find either $\begin{aligned} ∠ D \end{aligned}$ or $\begin{aligned} ∠ E \end{aligned}$ . We will find $\begin{aligned} ∠ D \end{aligned}$ first.
::现在我们知道F,我们知道三角形的三边。这意味着我们可以使用Casines定律来找到“D”或“E”。我们会先找到“D”。

\begin{aligned} 43^{2} & = {70.7}^{2} + 37^{2} - 2 (70.7) (37) \cos D \\ 1849 & = 6367.49 - 5231.8 \cos D \\ - 4518.49 & = - 5231.8 \cos D \\ 0.863658779 & = \cos D \\ {30.3}^{\circ} & \approx ∠ D \end{aligned}

::432=70.72+372-2(70.7)(37cosD1849=6367.49-5231.8cosD-4518.49523.8cosD0.86658779=cosD30.3D

To find $\begin{aligned} ∠ E \end{aligned}$ , we need only to use the Triangle Sum Theorem, $\begin{aligned} ∠ E = 180 - (124 + 30.3) = {25.7}^{\circ} \end{aligned}$ .
::要找到“E”,我们只需要使用“三角理论”,“E”=180-(124+30.3)=25.7。

3. In triangle $\begin{aligned} A B C, A = 43^{\circ}, B = 82^{\circ} \end{aligned}$ , and $\begin{aligned} c = 10.3 \end{aligned}$ . Solve the triangle.
::3. 在三角ABC,A=43,B=82和c=10.3。解决三角。

This is an example of the ASA case, which means that we can use the Law of Sines to solve the triangle. In order to use the Law of Sines, we must first know $\begin{aligned} ∠ C \end{aligned}$ , which we can find using the Triangle Sum Theorem, $\begin{aligned} ∠ C = 180^{\circ} - (43^{\circ} + 82^{\circ}) = 55^{\circ} \end{aligned}$ .
::这是ASA案例的一个例子,这意味着我们可以使用Sines定律来解决三角问题。为了使用Sines定律,我们必须首先知道QC,我们可以用三角Sum Theorem,QC=180(4382)=55。

Now that we know $\begin{aligned} ∠ C \end{aligned}$ , we can use the Law of Sines to find either side $\begin{aligned} a \end{aligned}$ or side $\begin{aligned} b . \end{aligned}$
::既然我们知道C, 我们可以用辛尼定律来找到任何一边或另一边的b。

\begin{aligned} \frac{\sin 55}{10.3} & = \frac{\sin 43}{a} & \frac{\sin 55}{10.3} = \frac{\sin 82}{b} \\ a & = \frac{10.3 \sin 43}{\sin 55} & b = \frac{10.3 \sin 82}{\sin 55} \\ a & = 8.6 & b = 12.5 \end{aligned}

::-=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

Examples
::实例

Example 1
::例1

Earlier, you were asked how you might help your sister find the lengths of the sides and the area of a non-right triangle.
::早些时候,有人问过你如何帮助你妹妹找到两边的长度以及一个非右三角的面积

Since you know that two of the angles are $\begin{aligned} 23^{\circ} \end{aligned}$ and $\begin{aligned} 28^{\circ} \end{aligned}$ , the third angle in the triangle must be $\begin{aligned} 180^{\circ} - 23^{\circ} - 28^{\circ} = 129^{\circ} \end{aligned}$ . Using these angles and the knowledge that one of the sides has a length of 4, you can solve for the lengths of the other two sides using the Law of Sines:
::既然你知道其中两个角度是 23 和 28 , 三角形中第三个角度必须是 180 23 28 129 。使用这些角度, 并知道其中一方的长度为 4, 您可以使用 Sines 法则解决另外两边的长度 :

\begin{aligned} \frac{\sin A}{a} = \frac{\sin B}{b} \\ \frac{\sin 23^{\circ}}{a} = \frac{\sin 129^{\circ}}{4} \\ a = \frac{4 \sin 23^{\circ}}{\sin 129^{\circ}} = \frac{1.56}{.777} \\ a \approx 2 \end{aligned}

::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译:

And repeating the process for the third side:
::并重复第三个方面的过程:

\begin{aligned} \frac{\sin A}{a} = \frac{\sin C}{c} \\ \frac{\sin 23^{\circ}}{2} = \frac{\sin 28^{\circ}}{c} \\ c = \frac{2 \sin 28^{\circ}}{\sin 23^{\circ}} = \frac{.939}{.781} \\ c \approx 1.2 \end{aligned}

::=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

Now you know all three angles and all three sides. You can use or the alternative formula for the area of a triangle to find the area:
::现在您知道所有三个角度和所有三个侧面。您可以使用或使用三角形区域的替代公式来找到区域 :

\begin{aligned} K = \frac{1}{2} b c \sin A \\ K = \frac{1}{2} (4) (1.2) \sin 23^{\circ} \\ K = \frac{1}{2} (4) (1.2) (.391) \\ K \approx .9384 \end{aligned}

::K=12bcsinAK=12(4)(1.2)sin23K=12(4)(1.2)(391)K9384

Example 2
::例2

Using the information provided, decide which case you are given (SSS, SAS, AAS, ASA, or SSA), and whether you would use the Law of Sines or the Law of Cosines to find the requested side or angle. Make an approximate drawing of the triangle and label the given information. Also, state how many solutions (if any) the triangle would have. If a triangle has no solution or two solutions, explain why.
::使用所提供的信息,决定给您提供哪种情况( SSS、 SAS、 AAS、 ASA 或 SSA) , 以及您是否会使用 Sines 法或 Cosines 法找到所请求的侧面或角度。绘制三角形的大致图和给定信息的标签。另外, 说明三角形会有多少解决方案( 如果有的话 ) 。如果三角形没有解决方案或两个解决方案, 请解释原因。

$\begin{aligned} A = 69^{\circ}, B = 12^{\circ}, a = 22.3 \end{aligned}$ , find $\begin{aligned} b \end{aligned}$
::A=69,B=12,a=22.3,找b

AAS, Law of Sines, one solution
::AAS,Sines定律,一个解决方案

Example 3
::例3

$\begin{aligned} a = 1.4, b = 2.3, C = 58^{\circ} \end{aligned}$ , find $\begin{aligned} c \end{aligned}$ .
::a=1.4,b=2.3,C=58,找c。

SAS, Law of Cosines, one solution
::SAS, Cosines定律,一个解决方案

Example 4
::例4

$\begin{aligned} a = 3.3, b = 6.1, c = 4.8 \end{aligned}$ , find $\begin{aligned} A \end{aligned}$ .
::a=3.3,b=6.1,c=4.8,见A。

SSS, Law of Cosines, one solution
::SSS, 共信定律, 一种解决办法

Review
::回顾

Using the information provided, decide which case you are given (SSS, SAS, AAS, ASA, or SSA), and whether you would use the Law of Sines or the Law of Cosines to find the requested side or angle. Make an approximate drawing of the triangle and label the given information. Also, state how many solutions (if any) the triangle would have.
::使用所提供的信息,决定您被给出的案件( SSS、 SAS、 AAS、 ASA 或 SSA) , 以及您是否将使用 Sines 法或 Cosines 法来找到所请求的侧面或角度。绘制三角形的大致图和给定信息的标签。另外, 说明三角形将有多少解决方案( 如果有的话 ) 。

$\begin{aligned} a = 3, b = 4, C = 71^{\circ} \end{aligned}$ , find $\begin{aligned} c \end{aligned}$ .
::a=3,b=4,C=71,找c。

$\begin{aligned} a = 8, b = 7, c = 9 \end{aligned}$ , find $\begin{aligned} A \end{aligned}$ .
::a=8,b=7,c=9,见A。

$\begin{aligned} A = 135^{\circ}, B = 12^{\circ}, c = 100 \end{aligned}$ , find $\begin{aligned} a \end{aligned}$ .
::A=135,B=12,c=100,找一个。

$\begin{aligned} a = 12, b = 10, A = 80^{\circ} \end{aligned}$ , find $\begin{aligned} c \end{aligned}$ .
::a=12,b=10,A=80,找c。

$\begin{aligned} A = 50^{\circ}, B = 87^{\circ}, a = 13 \end{aligned}$ , find $\begin{aligned} b \end{aligned}$ .
::A=50,B=87,a=13,找到b

In $\begin{aligned} △ A B C \end{aligned}$ , $\begin{aligned} a = 15, b = 19, c = 20 \end{aligned}$ . Solve the triangle.
::在 ABC 中, a= 15,b=19,c=20。解开三角形。

In $\begin{aligned} △ D E F \end{aligned}$ , $\begin{aligned} d = 12, E = 39^{\circ}, f = 17 \end{aligned}$ . Solve the triangle.
::在 DEF, d=12, E=39, f=17。解开三角形。

In $\begin{aligned} △ P Q R \end{aligned}$ , $\begin{aligned} P = 115^{\circ}, Q = 30^{\circ}, q = 10 \end{aligned}$ . Solve the triangle.
::在 QPQR, P=115, 30,q=10。解开三角形。

In $\begin{aligned} △ M N L \end{aligned}$ , $\begin{aligned} m = 5, n = 9, L = 20^{\circ} \end{aligned}$ . Solve the triangle.
::在“MNL”中, m=5,n=9,L=20。解决三角形。

In $\begin{aligned} △ S E V \end{aligned}$ , $\begin{aligned} S = 50^{\circ}, E = 44^{\circ}, s = 12 \end{aligned}$ . Solve the triangle.
::在 SEV 中, S=50, E=44, s=12。解开三角形。

In $\begin{aligned} △ K T S \end{aligned}$ , $\begin{aligned} k = 6, t = 15, S = 68^{\circ} \end{aligned}$ . Solve the triangle.
::在 QKTS 中, k=6, t=15, S=68。解开三角形。

In $\begin{aligned} △ W R S \end{aligned}$ , $\begin{aligned} w = 3, r = 5, s = 6 \end{aligned}$ . Solve the triangle.
::在WRS, w=3,r=5,s=6. 解开三角形。

In $\begin{aligned} △ D L P \end{aligned}$ , $\begin{aligned} D = 52^{\circ}, L = 110^{\circ}, p = 8 \end{aligned}$ . Solve the triangle.
::在“DLP”,D=52,L=110,p=8. 解决三角形。

In $\begin{aligned} △ X Y Z \end{aligned}$ , $\begin{aligned} x = 10, y = 12, z = 9 \end{aligned}$ . Solve the triangle.
::在XYZ, x=10,y=12,z=9. 解开三角形。

In $\begin{aligned} △ A M F \end{aligned}$ , $\begin{aligned} A = 99^{\circ}, m = 15, f = 16 \end{aligned}$ . Solve the triangle.
::在 AMF, A=99, m=15, f=16。解开三角形。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

三角通用解决方案

Finding Solutions for Triangles ::为三角寻找解决方案

Solving Triangles ::溶解三角形

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)