5.14 矢量添加

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 矢量加进

  Collapse Expand

  矢量加进

  播放段落

  You and a friend are pulling a box across a floor. However, each of you is pulling at a different angle. A diagram of your efforts looks like this:
  ::你和一个朋友在地板上拉着一个盒子。 但是,你们每个人都拉着一个不同的角度。你们努力的图表是这样的:

  

  播放段落

  Each of these forces is a vector. Can you determine the net force you and your friend are applying to the box? To find the net result of the effort, you need to add the vectors for each of the forces.
  ::这些力量中的每一力量都是矢量。 您可以确定您和您的朋友对盒子施用的净力 。 要找到努力的净结果, 您需要为每个力量添加矢量 。

  播放段落

  Adding Vectors
  ::添加矢量

  播放段落

  The sum of two or more vectors is called the of the vectors. There are two methods we can use to find the resultant: the parallelogram method and the triangle method.
  ::两个或两个以上矢量的总和被称为矢量的矢量。我们可以使用两种方法来找到结果:平行图法和三角法。

  播放段落

  The Parallelogram Method: Another method we could use is the parallelogram method. To use the parallelogram method, we draw the vectors so that their initial points meet. Then, we draw in lines to form a parallelogram. The resultant is the diagonal from the initial point to the opposite vertex of the parallelogram. It is important to note that we cannot use the parallelogram method to find the sum of a vector and itself .
  ::平行图方法: 另一种我们可以使用的方法是平行图方法。 为了使用平行图方法, 我们绘制矢量, 以便它们的初始点相交 。 然后, 我们绘制线条以形成平行图 。 其结果就是从初始点到平行图相反的顶点的对角。 必须指出的是, 我们无法使用平行图方法找到矢量和自身的总和 。

  

  播放段落

  To find the sum of the resultant vector, we would again use a ruler and a protractor to find the magnitude and direction.
  ::为了找到由此产生的矢量的总和, 我们将再次使用标尺和减速器 来找到数量和方向。

  播放段落

  If you look closely, you’ll notice that the parallelogram method is really a version of the triangle or tip-to-tail method. If you look at the top portion of the figure above, you can see that one side of our parallelogram is really vector $\begin{array}{r}b\end{array}$ translated.
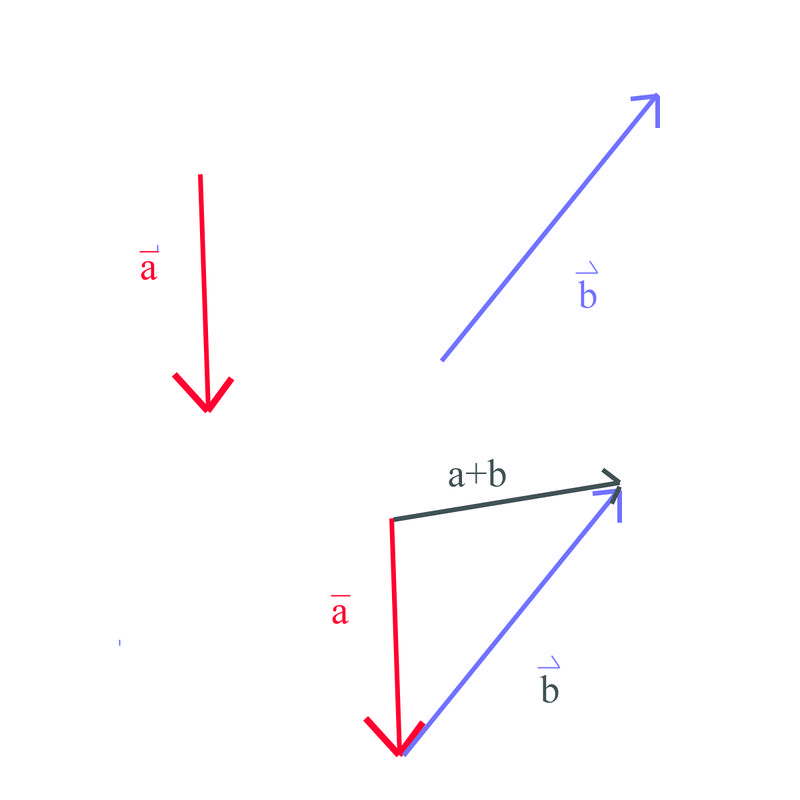
  ::如果您仔细看一看, 您就会注意到平行图法实际上是三角形的版本, 或者从小到尾的方法。 如果您查看以上图的顶部, 您可以看到我们平行图的一面真的翻译了矢量 b 。

  

  播放段落

  The Triangle Method: To use the triangle method, we draw the vectors one after another and place the initial point of the second vector at the terminal point of the first vector. Then, we draw the resultant vector from the initial point of the first vector to the terminal point of the second vector. This method is also referred to as the tip-to-tail method .
  ::三角方法 : 要使用三角法, 我们将矢量逐个绘制, 然后将第二个矢量的初始点放在第一个矢量的终端点。 然后, 我们将由此产生的矢量从第一个矢量的初始点拖到第二个矢量的终端点。 这个方法也被称为小到尾方法 。

  

  播放段落

  To find the sum of the resultant vector we would use a ruler and a protractor to find the magnitude and direction.
  ::为了找到由此产生的矢量的总和,我们将使用标尺和减速器来找到星度和方向。

  播放段落

  The resultant vector can be much longer than either $\begin{array}{r}\stackrel{\to }{a}\end{array}$ or $\begin{array}{r}\stackrel{\to }{b}\end{array}$ , or it can be shorter. Below are some more examples of the triangle method.
  ::由此产生的矢量可能比 a 或 b 或 长得多, 也可能更短。 下面是三角法的一些例子 。

  播放段落

  Solve the following problems below using the triangle method.
  ::使用三角法解决以下问题 。

  1.

  

  2. 

  

  3. 

  

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to determine the net force you and your friend are applying to the box. 
  ::早些时候,你被要求确定 你和你朋友申请的 净力

  播放段落

  A triangle method diagram of the vectors being added looks like this:
  ::所添加矢量的三角方法图表看起来是这样 :

  

  播放段落

  As you can see, the resultant force has a magnitude of 100 Newtons at an angle of $\begin{array}{r}{45}^{\circ }\end{array}$
  ::如你所见 后继力在45度角的100牛顿 高度为100牛顿

  播放段落

  Example 2
  ::例2

  播放段落

  Vectors $\begin{array}{r}\stackrel{\to }{m}\end{array}$ and $\begin{array}{r}\stackrel{\to }{n}\end{array}$ are perpendicular. Make a diagram of each addition, find the magnitude and direction (with respect to $\begin{array}{r}\stackrel{\to }{m}\end{array}$ and $\begin{array}{r}\stackrel{\to }{n}\end{array}$ ) of their resultant if $\begin{array}{r}|\stackrel{\to }{m}|=29.8|\stackrel{\to }{n}|=37.7\end{array}$
  ::矢量 m 和 n 是垂直的。 绘制每增加的图表, 找到其结果的大小和方向( 相对于 m 和 n) , 如果 \\ m 29. 8 n 37.7 的话 。

  播放段落

  For the problem, use the Pythagorean Theorem to find the magnitude and $\begin{array}{r}\tan \theta =\frac{|\stackrel{\to }{n}|}{|\stackrel{\to }{m}|}\end{array}$
  ::对于问题,请使用毕达哥里安神话来找出其规模和程度。

  播放段落

  magnitude $\begin{array}{r}=48.1\end{array}$ , direction $\begin{array}{r}={51.7}^{\circ }\end{array}$
  ::级数 = 48.1, 方向 = 51.7

  播放段落

  Example 3
  ::例3

  播放段落

  Vectors $\begin{array}{r}\stackrel{\to }{m}\end{array}$ and $\begin{array}{r}\stackrel{\to }{n}\end{array}$ are perpendicular. Make a diagram of each addition, find the magnitude and direction (with respect to $\begin{array}{r}\stackrel{\to }{m}\end{array}$ and $\begin{array}{r}\stackrel{\to }{n}\end{array}$ ) of their resultant if $\begin{array}{r}|\stackrel{\to }{m}|=2.8|\stackrel{\to }{n}|=5.4\end{array}$
  ::矢量 m 和 n 是垂直的。 绘制每增加的图表, 找到其结果的大小和方向( 相对于 m 和 n ) , 如果 \\ m 2. 8 n 5. 4 的话 。

  播放段落

  For the problem, use the Pythagorean Theorem to find the magnitude and $\begin{array}{r}\tan \theta =\frac{|\stackrel{\to }{n}|}{|\stackrel{\to }{m}|}\end{array}$
  ::对于问题,请使用毕达哥里安神话来找出其规模和程度。

  播放段落

  magnitude $\begin{array}{r}=6.1\end{array}$ , direction $\begin{array}{r}={62.6}^{\circ }\end{array}$
  ::级数=6.1,方向=62.6

  播放段落

  Example 4
  ::例4

  播放段落

  Vectors $\begin{array}{r}\stackrel{\to }{m}\end{array}$ and $\begin{array}{r}\stackrel{\to }{n}\end{array}$ are perpendicular. Make a diagram of each addition, find the magnitude and direction (with respect to $\begin{array}{r}\stackrel{\to }{m}\end{array}$ and $\begin{array}{r}\stackrel{\to }{n}\end{array}$ ) of their resultant if $\begin{array}{r}|\stackrel{\to }{m}|=11.9|\stackrel{\to }{n}|=9.4\end{array}$
  ::矢量 m 和 n 是垂直的。 绘制每增加的图表, 找到其结果的大小和方向( 相对于 m 和 n) , 如果 \\\\\\ 11. 9\\\ n 9. 4 的话 。

  播放段落

  For the problem, use the Pythagorean Theorem to find the magnitude and $\begin{array}{r}\tan \theta =\frac{|\stackrel{\to }{n}|}{|\stackrel{\to }{m}|}\end{array}$
  ::对于问题,请使用毕达哥里安神话来找出其规模和程度。

  播放段落

  magnitude $\begin{array}{r}=15.2\end{array}$ , direction $\begin{array}{r}={38.3}^{\circ }\end{array}$
  ::等量=15.2,方向=38.3

  播放段落

  Review
  ::回顾

  播放段落

  $\begin{array}{r}\stackrel{\to }{a}\end{array}$ is in standard position with terminal point (1, 5) and $\begin{array}{r}\stackrel{\to }{b}\end{array}$ is in standard position with terminal point (4, 2).
  ::a 处于标准位置,有终点(1,5),b 处于标准位置,有终点(4,2)。

  播放段落
  1. Find the coordinates of the terminal point of the resultant vector.
     ::查找结果矢量的终点点的坐标 。
  播放段落
  2. What is the magnitude of the resultant vector?
     ::由此产生的矢量的大小是多少?
  播放段落
  3. What is the direction of the resultant vector?
     ::由此产生的矢量的方向是什么?

  播放段落

  $\begin{array}{r}\stackrel{\to }{c}\end{array}$ is in standard position with terminal point (4, 3) and $\begin{array}{r}\stackrel{\to }{d}\end{array}$ is in standard position with terminal point (2, 2).
  ::c 处于标准位置,有终点点(4,3),d 处于标准位置,有终点点(2,2))。

  播放段落
  4. Find the coordinates of the terminal point of the resultant vector.
     ::查找结果矢量的终点点的坐标 。
  播放段落
  5. What is the magnitude of the resultant vector?
     ::由此产生的矢量的大小是多少?
  播放段落
  6. What is the direction of the resultant vector?
     ::由此产生的矢量的方向是什么?

  播放段落

  $\begin{array}{r}\stackrel{\to }{e}\end{array}$ is in standard position with terminal point (3, 2) and $\begin{array}{r}\stackrel{\to }{f}\end{array}$ is in standard position with terminal point (-1, 2).
  ::e处于标准位置,终点点(3,2)和F处于标准位置,终点点(1,2)为标准位置。

  播放段落
  7. Find the coordinates of the terminal point of the resultant vector.
     ::查找结果矢量的终点点的坐标 。
  播放段落
  8. What is the magnitude of the resultant vector?
     ::由此产生的矢量的大小是多少?
  播放段落
  9. What is the direction of the resultant vector?
     ::由此产生的矢量的方向是什么?

  播放段落

  $\begin{array}{r}\stackrel{\to }{g}\end{array}$ is in standard position with terminal point (5, 5) and $\begin{array}{r}\stackrel{\to }{h}\end{array}$ is in standard position with terminal point (4, 2).
  ::g 处于标准位置,端点(5,5),h 处于标准位置,端点(4,2),端点(4,2)

  播放段落
  10. Find the coordinates of the terminal point of the resultant vector.
      ::查找结果矢量的终点点的坐标 。
  播放段落
  11. What is the magnitude of the resultant vector?
      ::由此产生的矢量的大小是多少?
  播放段落
  12. What is the direction of the resultant vector?
      ::由此产生的矢量的方向是什么?

  播放段落

  $\begin{array}{r}\stackrel{\to }{i}\end{array}$ is in standard position with terminal point (1, 5) and $\begin{array}{r}\stackrel{\to }{j}\end{array}$ is in standard position with terminal point (-3, 1).
  ::i 处于标准位置,有终点(1,5),j 处于标准位置,有终点(-3,1)。

  播放段落
  13. Find the coordinates of the terminal point of the resultant vector.
      ::查找结果矢量的终点点的坐标 。
  播放段落
  14. What is the magnitude of the resultant vector?
      ::由此产生的矢量的大小是多少?
  播放段落
  15. What is the direction of the resultant vector?
      ::由此产生的矢量的方向是什么?
  播放段落
  16. Vectors $\begin{array}{r}\stackrel{\to }{k}\end{array}$ and $\begin{array}{r}\stackrel{\to }{l}\end{array}$ are perpendicular. Make a diagram of each addition, find the magnitude and direction (with respect to $\begin{array}{r}\stackrel{\to }{k}\end{array}$ and $\begin{array}{r}\stackrel{\to }{l}\end{array}$ ) of their resultant if $\begin{array}{r}|\stackrel{\to }{k}|=42\end{array}$ and $\begin{array}{r}|\stackrel{\to }{l}|=30\end{array}$ .
      ::k 和 l 是垂直的 矢量 k 和 l 。 绘制每增加一个图表, 找到其结果的大小和方向( k 和 l) , 如果 k 42 和 l 30 。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。