3.1 检查线性系统的解决方案

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节检查线性系统的解决方案

  折叠 展开

  检查线性系统的解决方案

  播放段落

  The Hiking Club is buying nuts to make trail mix for a fundraiser. Three pounds of almonds and two pounds of cashews cost a total of $36. Three pounds of cashews and two pounds of almonds cost a total of $39. Is ( a , c ) = ($6, $9) a solution to this system?
  ::三磅杏仁和两磅腰果总共需要36美元。 三磅腰果和两磅杏仁总共需要39美元。 (a, c) = (6, 9) 是这个系统的解决办法吗?

  播放段落

  Solution to a System of Linear Equations
  ::线线性等式系统解决方案

  播放段落

  A system of linear equations consists of the equations of two lines. The solution to a system of linear equations is the point which lies on both lines. In other words, the solution is the point where the two lines intersect. To verify whether a point is a solution to a system or not, we will either determine whether it is the point of intersection of two lines on a graph or we will determine whether or not the point lies on both lines algebraically.
  ::线性方程式系统由两行的方程式组成。 线性方程式系统的解决方案是两行的点。 换句话说, 解决方案是两行交叉的点。 要验证一个点是否是一个系统的解决方案, 我们要么确定它是否是一个图形上两行的交叉点, 要么我们确定该点是否位于两行的代数线上。

  播放段落

  Let's determine whether the given points are a solution to the systems of equations below.
  ::让我们来决定给定的点数是否是以下方程式系统的解决办法。

  播放段落
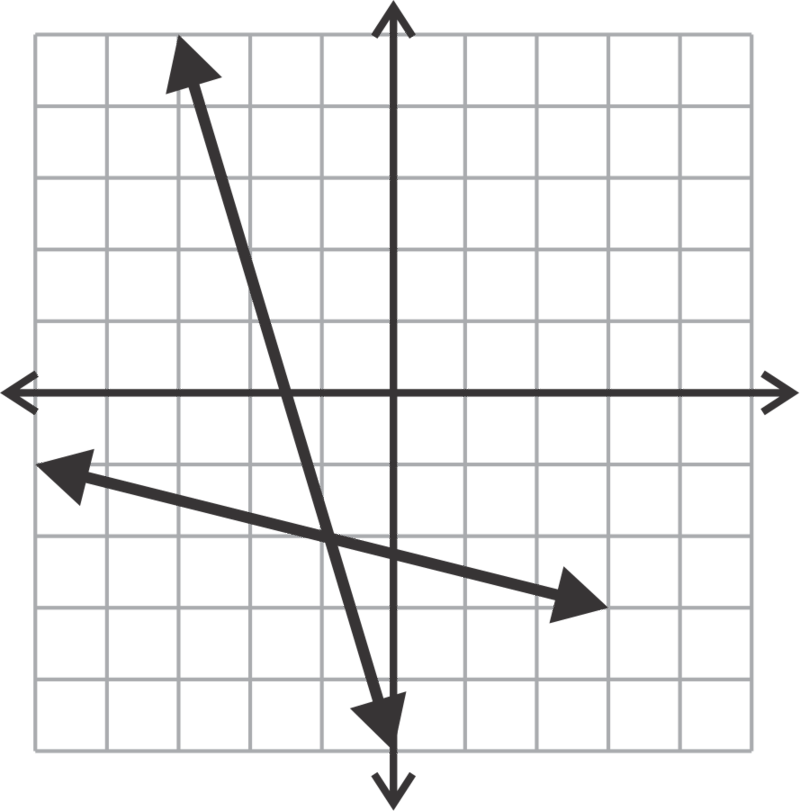
  1. Is the point (5, -2) the solution of the system of linear equations shown in the graph below?
     ::点(5, 2)是否是下图所示线性方程式系统的解决办法?

  

  播放段落

  Yes, the lines intersect at the point (5, -2) so it is the solution to the system.
  ::是的,线在点(5,2)交叉,所以这是系统的解决办法。

  播放段落
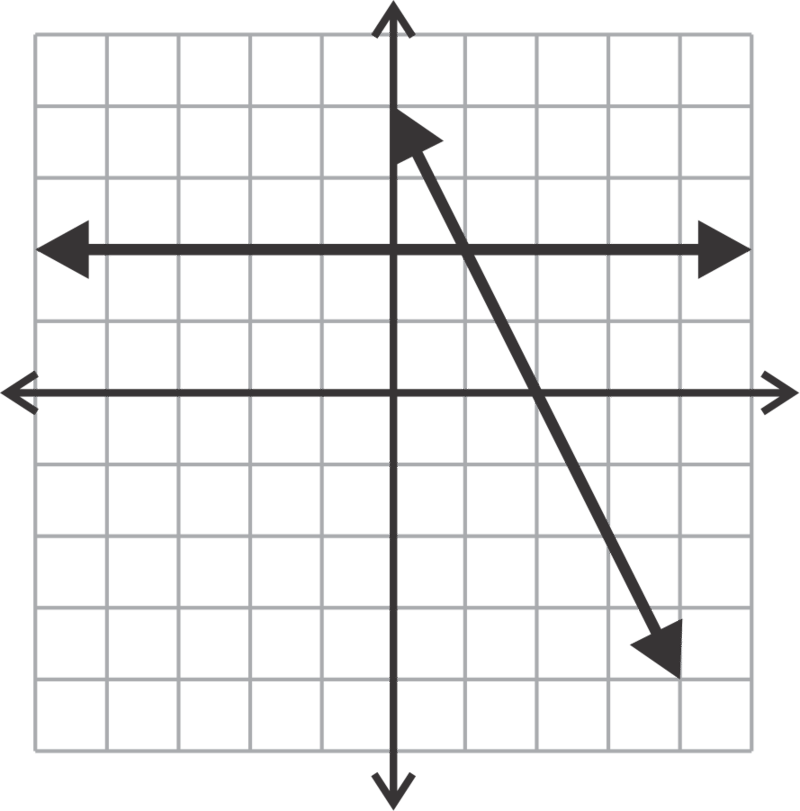
  2. Is the point (-3, 4) the solution to the system given below?
     ::要点(-3,4)是否是下文所述系统的解决办法?

  播放段落

  $$\begin{array}{rl}2x-3y& =-18\\ x+2y& =6\end{array}$$

  
  ::2 - 3y18x+2y=6

  播放段落

  No, (-3, 4) is not the solution. If we replace the $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ in each equation with -3 and 4 respectively, only the first equation is true. The point is not on the second line; therefore it is not the solution to the system.
  ::否, (3, 4) 不是解决方案。 如果我们将每个方程中的 x 和 y 分别替换为 - 3 和 4, 只有第一个方程是真实的。 点不在第二行, 因此不是系统的解决办法 。

  播放段落

  Now, let's find the solution to the system below.
  ::现在,让我们找出下面系统的解决办法。

  播放段落

  $$\begin{array}{rl}x& =5\\ 3x-2y& =25\end{array}$$

  
  ::x=53x--2y=25

  播放段落

  Because the first line in the system is vertical , we already know the x -value of the solution, $\begin{array}{r}x=5\end{array}$ . Plugging this into the second equation, we can solve for y .
  ::因为系统中的第一行是垂直的, 我们已经知道溶液的 X 值, x= 5 。 将它插进第二个方程, 我们可以解决y 。

  播放段落

  $$\begin{array}{rl}3(5)-2y& =25\\ 15-2y& =25\\ -2y& =10\\ y& =-5\end{array}$$

  
  ::3(5)-2y=2515-2y=25-2y=10y=10y5

  播放段落

  The solution is (5, -5). Check your solution to make sure it's correct.
  ::答案是 (5,5,5) 检查你的解决方案以确保它是正确的 。

  $$\begin{array}{rl}3(5)-2(-5)& =25\\ 15+10& =25\end{array}$$

  播放段落

  You can also solve systems where one line is horizontal in this manner.
  ::您也可以用这种方式解析一条线是水平线的系统 。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked if (a, c) = ($6, $9) is a solution to the system of equations .
  ::早些时候,有人问你(a, c) = (6, 9) 是否是方程式系统的解决办法。

  播放段落

  The system of linear equations represented by this situation is:
  ::以这种情况为代表的线性方程式系统是:

  播放段落

  $$\begin{array}{rl}3a+2c& =36\\ 3c+2a& =39\end{array}$$

  
  ::3a+2c=363c+2a=39

  播放段落

  If we plug in $6 for a and $9 for c , both equations are true. Therefore ($6, $9) is a solution to the system.
  ::如果我们用6美元加1美元和9美元加C,这两个方程式都是真实的。因此(6,9美元)是系统的解决办法。

  播放段落

  Example 2
  ::例2

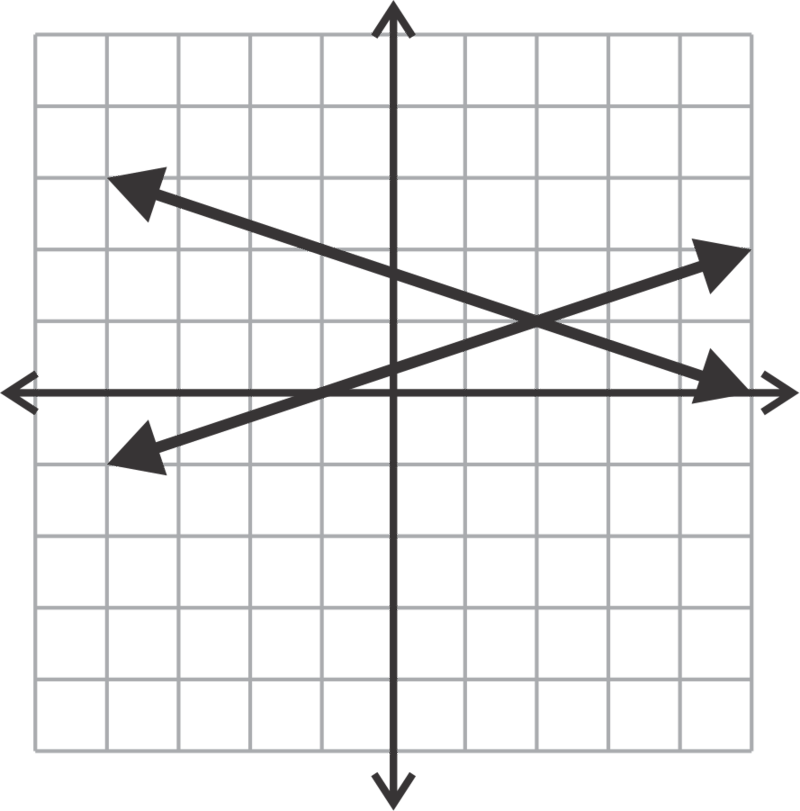
  播放段落

  Is the point (-2, 1) the solution to the system shown below?
  ::要点(-2,1)是否是下文所述系统的解决办法?

  

  播放段落

  No, (-2, 1) is not the solution. The solution is where the two lines intersect which is the point (-3, 1).
  ::否, (-2, 1) 不是解决办法, 解决办法是两条线相交之处, 也就是点( -3, 1) 。

  播放段落

  Example 3
  ::例3

  播放段落

  Verify algebraically that (6, -1) is the solution to the system shown below.
  ::校验代数(6,-1)是以下系统的解决办法。

  播放段落

  $$\begin{array}{rl}3x-4y& =22\\ 2x+5y& =7\end{array}$$

  
  ::3x-4y=222x+5y=7

  播放段落

  By replacing $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ in both equations with 6 and -1 respectively (shown below), we can verify that the point (6, -1) satisfies both equations and thus lies on both lines.
  ::通过将两个方程中的x和y分别替换为6和-1(如下文所示),我们可以核实点(6,-1)满足了两个方程,因此是两个线的。

  $$\begin{array}{rl}3(6)-4(-1)& =18+4=22\\ 2(6)+5(-1)& =12-5=7\end{array}$$

  播放段落

  Example 4
  ::例4

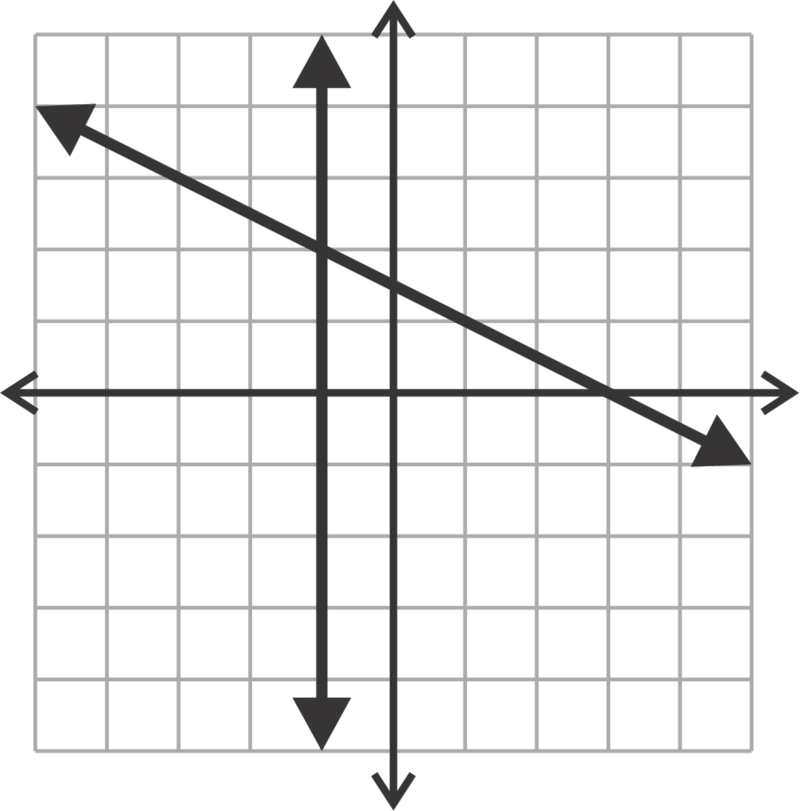
  播放段落

  Explain why the point (3, 7) is the solution to the system:
  ::解释为何系统的解决办法(3、7)是:

  播放段落

  $$\begin{array}{rl}y& =7\\ x& =3\end{array}$$

  
  ::y=7x=3 y=7x=3

  播放段落

  The horizontal line is the line containing all points where the $\begin{array}{r}y-\end{array}$ coordinate 7. The vertical line is the line containing all points where the $\begin{array}{r}x-\end{array}$ coordinate 3. Thus, the point (3, 7) lies on both lines and is the solution to the system.
  ::7. 垂直线是包含X-坐标3的所有点的线条。 因此,两条线上都有点(3、7),是系统的解决办法。

  播放段落

  Review
  ::回顾

  播放段落

  Match the solutions with their systems.
  ::解决方案与其系统匹配。

  1. (1, 2)
     1. 
     2. 
     3. 
     4. 

  2. (2, 1)
     1. 
     2. 
     3. 
     4. 

  3. (-1, 2)
     1. 
     2. 
     3. 
     4. 

  4. (-1, -2)
     1. 
     2. 
     3. 
     4. 

  播放段落

  Determine whether each ordered pair represents the solution to the given system.
  ::确定每对定购夫妇是否代表给定系统的解决方案。

  5. .

  $$\begin{array}{rl}4x+3y& =12\\ 5x+2y& =1;(-3,8)\end{array}$$

  6. .

  $$\begin{array}{rl}3x-y& =17\\ 2x+3y& =5;(5,-2)\end{array}$$

  7. .

  $$\begin{array}{rl}7x-9y& =7\\ x+y& =1;(1,0)\end{array}$$

  8. .

  $$\begin{array}{rl}x+y& =-4\\ x-y& =4;(5,-9)\end{array}$$

  9. .

  $$\begin{array}{rl}x& =11\\ y& =10;(11,10)\end{array}$$

  10. .

  $$\begin{array}{rl}x+3y& =0\\ y& =-5;(15,-5)\end{array}$$

  播放段落

  Find the solution to each system below.
  ::为下面的每个系统找出解决办法。

  11. .

  $$\begin{array}{rl}x& =-2\\ y& =4\end{array}$$

  12. .

  $$\begin{array}{rl}y& =-1\\ 4x-y& =13\end{array}$$

  13. .

  $$\begin{array}{rl}x& =7\\ y& =6\end{array}$$

  14. .

  $$\begin{array}{rl}x& =2\\ 8x+3y& =-11\end{array}$$

  播放段落
  15. Describe the solution to a system of linear equations.
      ::描述线性方程式系统的解决方案 。
  播放段落
  16. Can you think of why a linear system of two equations would not have a unique solution?
      ::你能想到两个方程式的线性系统 为何没有独特的解决方案吗?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。