5.15 矢量减法

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 矢量减法

  Collapse Expand

  矢量减法

  播放段落

  You and a friend are trying to position a heavy sculpture out in front of your school. Fortunately, the sculpture is on rollers, so you can move it around easily and slide it into place. While you are applying force to the sculpture, it starts to move. The vectors you and your friend are applying look like this:
  ::你和一个朋友正试图将一个重雕塑放在学校前面。幸运的是,雕塑在滚滚机上,这样你就可以轻而易举地移动它,然后滑到位置上。当你对雕塑施力时,它开始移动。你和你朋友的矢量都像这样应用:

  

  播放段落

  However, the sculpture starts to move too far and overshoots where it is supposed to be. You quickly tell your friend to pull instead of push, in effect subtracting her force vector, where before it was being added. Can you represent this graphically?
  ::然而, 雕塑开始移动太远, 并且超标了 。 您会很快地告诉您的朋友拉而不是推, 从而在添加它之前, 减去她的矢量 。 您能用图形来表达吗 ?

  播放段落

  Subtracting Vectors
  ::减量矢量

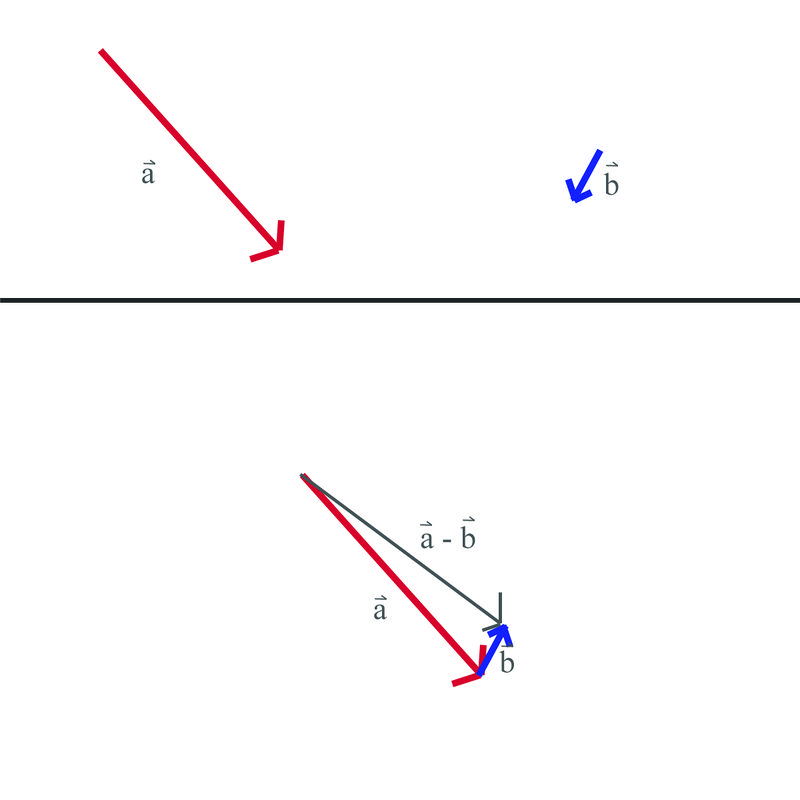
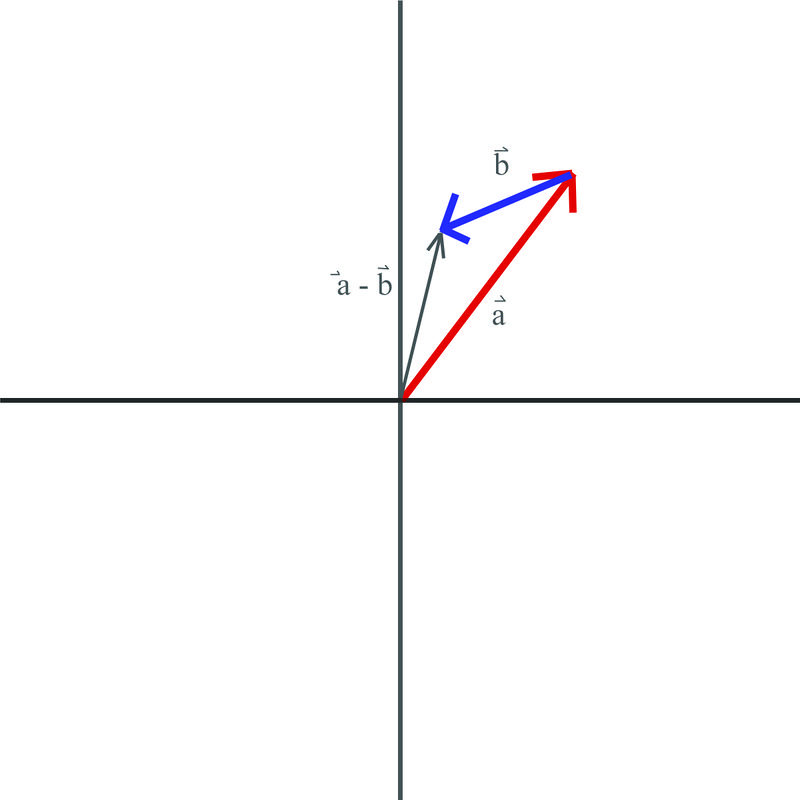
  播放段落

  As you know from Algebra, $\begin{array}{r}A-B=A+(-B)\end{array}$ . When we think of vector subtraction, we must think about it in terms of adding a negative vector.
  ::正如您从代数A-B=A+(-B)中知道的那样。当我们想到矢量减量时,我们必须考虑增加负矢量。

  播放段落

   A negative vector is the same magnitude of the original vector, but its direction is opposite.
  ::负向量与原向量的负向量相同,但其方向相反。

  

  播放段落

  In order to subtract two vectors, we can use either the triangle method or the parallelogram method from above. The only difference is that instead of adding vectors $\begin{array}{r}A\end{array}$ and $\begin{array}{r}B\end{array}$ , we will be adding $\begin{array}{r}A\end{array}$ and $\begin{array}{r}-B\end{array}$ .
  ::为了减去两个矢量, 我们可以使用三角法或从以上平行图示法。 唯一的区别是, 我们不用添加矢量 A 和 B, 而是要添加 A 和 B 。

  播放段落

  Let's solve the following problems using the triangle method for subtraction
  ::让我们用三角形的减法解决以下问题

  1. 

  

  

  2. 

  

  3. 

  

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to represent your work graphically. 
  ::早些时候,有人要求你以图形方式代表你的工作。

  播放段落

  As you've seen in this Concept, subtracting a vector is the same as adding the negative of the original vector. This is exactly like the rule for adding a negative number to a positive number. Therefore, to change your friend's force vector to a subtraction instead of an addition, you need to change the direction by $\begin{array}{r}{180}^{\circ }\end{array}$ while keeping the magnitude the same. The graph looks like this:
  ::正如您在此概念中看到的那样, 减去矢量与添加原始矢量的负值相同。 这和在正数中添加负数的规则完全相同。 因此, 要将您朋友的强制矢量修改为减法而不是加法, 您需要将方向修改为 180\\\\\ , 并保持不变的数值 。 图表是这样 :

  

  播放段落

  Example 2
  ::例2

  播放段落

  For the vector subtraction below, make a diagram of the subtraction. $\begin{array}{r}\stackrel{\to }{a}-\stackrel{\to }{d}\end{array}$
  ::对于下面的矢量减法,请绘制一个减法图表。

  

  播放段落

  Example 3
  ::例3

  播放段落

  For the vector subtraction below, make a diagram of the subtraction. $\begin{array}{r}\stackrel{\to }{b}-\stackrel{\to }{a}\end{array}$
  ::对于下面的矢量减法,请绘制一个减法图。

  

  播放段落

  Example 4
  ::例4

  播放段落

  For the vector subtraction below, make a diagram of the subtraction. $\begin{array}{r}\stackrel{\to }{d}-\stackrel{\to }{c}\end{array}$
  ::对于下面的矢量减法,请绘制一个减法图。

  

  播放段落

  Review
  ::回顾

  播放段落

  $\begin{array}{r}\stackrel{\to }{a}\end{array}$ is in standard position with terminal point (1, 5) and $\begin{array}{r}\stackrel{\to }{b}\end{array}$ is in standard position with terminal point (4, 2).
  ::a 处于标准位置,有终点(1,5),b 处于标准位置,有终点(4,2)。

  播放段落
  1. Find the coordinates of the terminal point of $\begin{array}{r}\stackrel{\to }{a}-\stackrel{\to }{b}\end{array}$ .
     ::查找 ab的终点点的坐标 。
  播放段落
  2. What is the magnitude of $\begin{array}{r}\stackrel{\to }{a}-\stackrel{\to }{b}\end{array}$ ?
     ::是什么程度的ABQQQQQQQQQQQQ?
  播放段落
  3. What is the direction of $\begin{array}{r}\stackrel{\to }{a}-\stackrel{\to }{b}\end{array}$ ?
     ::什么是方向 ab?

  播放段落

  $\begin{array}{r}\stackrel{\to }{c}\end{array}$ is in standard position with terminal point (4, 3) and $\begin{array}{r}\stackrel{\to }{d}\end{array}$ is in standard position with terminal point (2, 2).
  ::c 处于标准位置,有终点点(4,3),d 处于标准位置,有终点点(2,2))。

  播放段落
  4. Find the coordinates of the terminal point of $\begin{array}{r}\stackrel{\to }{c}-\stackrel{\to }{d}\end{array}$ .
     ::查找 cd的终点点的坐标 。
  播放段落
  5. What is the magnitude of $\begin{array}{r}\stackrel{\to }{c}-\stackrel{\to }{d}\end{array}$ ?
     ::CQDQQQQQQQQQQQQQQQQQQDQQQQQQQQQQQQQDQQQQQQQQQQQQQQQQQDQQQQQQQQQQQQQQQQQQQDQQQQQQQQQQQDQQQQQQQQQQQQDQQQQQQQQQQQQQQQQQQDQQDQQQQQQQQDQQQQQQDQQQQQQQQQQDQQQQDQQQQQQQQQQQQQDQQQQQQQQQQQQQQQQQQDQQQQQQQQQQQQDQQQQQQQQQQQQQQQQQQQQQDQQQQQQDQDQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ的大小的大小的大小的大小的大小的大小的大小的大小的大小大小大小的大小大小大小大小的大小大小大小的大小大小 的大小 的大小 的大小? QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ
  播放段落
  6. What is the direction of $\begin{array}{r}\stackrel{\to }{c}-\stackrel{\to }{d}\end{array}$ ?
     ::Cd的方向是什么?

  播放段落

  $\begin{array}{r}\stackrel{\to }{e}\end{array}$ is in standard position with terminal point (3, 2) and $\begin{array}{r}\stackrel{\to }{f}\end{array}$ is in standard position with terminal point (-1, 2).
  ::e处于标准位置,终点点(3,2)和F处于标准位置,终点点(1,2)为标准位置。

  播放段落
  7. Find the coordinates of the terminal point of $\begin{array}{r}\stackrel{\to }{e}-\stackrel{\to }{f}\end{array}$ .
     ::查找 ef的终点点的坐标 。
  播放段落
  8. What is the magnitude of $\begin{array}{r}\stackrel{\to }{e}-\stackrel{\to }{f}\end{array}$ ?
     ::ef的大小是多少?
  播放段落
  9. What is the direction of $\begin{array}{r}\stackrel{\to }{e}-\stackrel{\to }{f}\end{array}$ ?
     ::什么是方向 ef?

  播放段落

  $\begin{array}{r}\stackrel{\to }{g}\end{array}$ is in standard position with terminal point (5, 5) and $\begin{array}{r}\stackrel{\to }{h}\end{array}$ is in standard position with terminal point (4, 2).
  ::g 处于标准位置,端点(5,5),h 处于标准位置,端点(4,2),端点(4,2)

  播放段落
  10. Find the coordinates of the terminal point of $\begin{array}{r}\stackrel{\to }{g}-\stackrel{\to }{h}\end{array}$ .
      ::查找 gh的终点点的坐标 。
  播放段落
  11. What is the magnitude of $\begin{array}{r}\stackrel{\to }{g}-\stackrel{\to }{h}\end{array}$ ?
      ::GQHQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQHHQQQQQQQQQQQQQQQQQQQQQQQQHQQQQQQQQQQQQQQQQQQQQQHQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQOQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ的大小的大小的大小的大小 的大小 的大小 的大小 的大小? 的大小? 的大小? 的大小? 的大小? 大小
  播放段落
  12. What is the direction of $\begin{array}{r}\stackrel{\to }{g}-\stackrel{\to }{h}\end{array}$ ?
      ::什么是gh的方向?

  播放段落

  $\begin{array}{r}\stackrel{\to }{i}\end{array}$ is in standard position with terminal point (1, 5) and $\begin{array}{r}\stackrel{\to }{j}\end{array}$ is in standard position with terminal point (-3, 1).
  ::i 处于标准位置,有终点(1,5),j 处于标准位置,有终点(-3,1)。

  播放段落
  13. Find the coordinates of the terminal point of $\begin{array}{r}\stackrel{\to }{i}-\stackrel{\to }{j}\end{array}$ .
      ::查找 ij 的终点点的坐标 。
  播放段落
  14. What is the magnitude of $\begin{array}{r}\stackrel{\to }{i}-\stackrel{\to }{j}\end{array}$ ?
      ::是什么程度的ij?
  播放段落
  15. What is the direction of $\begin{array}{r}\stackrel{\to }{i}-\stackrel{\to }{j}\end{array}$ ?
      ::什么是方向 ij?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。