Course: 3.2 使用图形图解的单一解决办法的溶解系统

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 使用图形图解的单一解决办法的解决系统

Collapse Expand
使用图形图解的单一解决办法的解决系统
Two of coin $\begin{align*}a\end{align*}$ plus four of coin $\begin{align*}b\end{align*}$ equals a total of 70 cents. One of coin $\begin{align*}a\end{align*}$ plus five of coin $\begin{align*}b\end{align*}$ equals a total of 50 cents. What is the value of each type of coin?
::一枚硬币加五硬币等于50美分。每种硬币的价值是多少?

Solving Systems by Graphing
::通过图表绘制的解决系统

In this lesson we will be using various techniques to graph the pairs of lines in systems of linear equations to identify the point of intersection , which is the solution to the system. It is important to use graph paper and a straightedge to graph the lines accurately. Also, you are encouraged to check your answer algebraically to verify your work.
::在此教训中, 我们将使用各种技术来绘制线性方程系统中的线条配对图, 以辨别交叉点, 这是系统的解决办法。重要的是要使用图形纸和直线来精确地绘制线条。另外, 鼓励您检查您的答案代数, 以校验您的工作。

Let's solve the following systems by graphing.
::让我们通过图形化来解决以下系统。

Graph and solve the system: $\begin{align*}\begin{cases} y=\text{-}x+1\\ y=\frac{1}{2}x-2 \end{cases}\end{align*}$
::图形和解析系统 : {y=- x+1y=12x-2

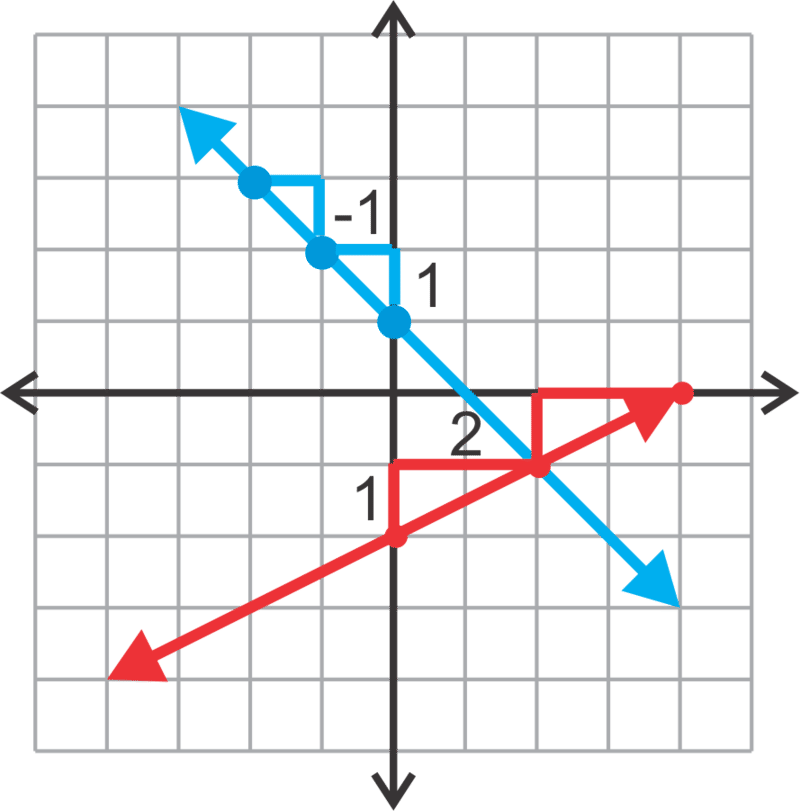
Since both of these equations are written in intercept form , graph them by plotting the $\begin{align*}y-\end{align*}$ intercept point and using the slope to locate additional points on each line.
::由于这两个方程式都是以截取形式写成的,因此通过绘制y-截取点和用斜坡确定每一行的其他点来绘制它们图。

The equation $\begin{align*}y=\text{-}x+1,\end{align*}$ graphed in $\begin{align*}{\color{blue}\mathbf{blue}}\end{align*}$ , has $\begin{align*}y-\end{align*}$ intercept 1 and slope $\begin{align*}\text{-} \frac{1}{1}\end{align*}$ .
::y=-x+1方程式,以蓝色图表显示,有y-intercut 1和斜度-11。

The equation $\begin{align*}y=\frac{1}{2}x-2,\end{align*}$ graphed in $\begin{align*}{\color{red}\mathbf{red}}\end{align*}$ , has $\begin{align*}y-\end{align*}$ intercept -2 and slope $\begin{align*}\frac{1}{2}\end{align*}$ .
::y=12x-2等式,以红色图表显示,有y-intercept-2和斜度12。

Now that both lines have been graphed, the intersection is easy to see at the point (2, -1).
::现在两条线都用图示了, 十字路口在点( 2, - 1) 很容易看到。

Check this solution algebraically by substituting the point into both equations.
::将点替换为两个方程式, 从代数中检查此解决方案。

Equation 1, $\begin{align*}y=-x+1\end{align*}$ : making the substitution gives: $\begin{align*}(\text{-}1)=(\text{-}2)+1. \end{align*}$
::方程式 1 yx+1 : 使替换提供 (-1) = (-2) +1 。

Equation 2, $\begin{align*}y=\frac{1}{2}x-2\end{align*}$ : making the substitution gives: $\begin{align*}\text{-}1=\frac{1}{2}(2)-2. \end{align*}$
::方程式 2 y= 12x-2 : 使替换提供 - 1= 12(2)-2 。

(2, -1) is the solution to the system.
:2,-1)是系统的解决办法。

Graph and solve the system: $\begin{align*}\begin{cases}3x+2y = 6\\ y = \text{-}\frac{1}{2}x-1 \end{cases}\end{align*}$
::图形和解析系统 : {3x+2y=6y=12x- 1

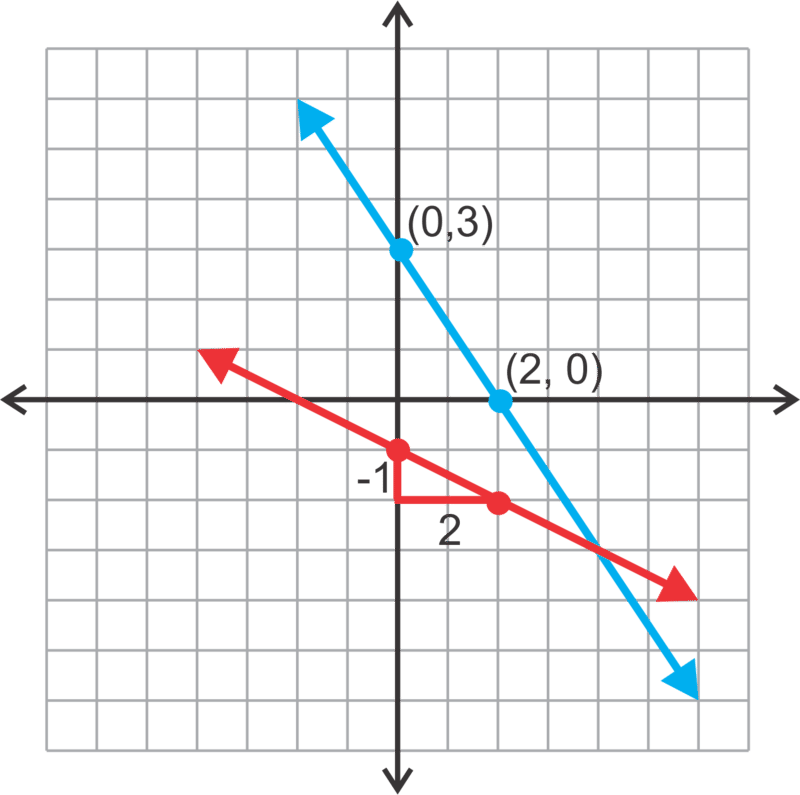
This problem is very similar to the previous problem . The only difference is that equation 1 is not in slope intercept form. We can either solve for $\begin{align*}y\end{align*}$ to put it in slope intercept form or we can use the intercepts to graph the equation. To review using intercepts to graph lines, we will use the latter method.
::这个问题与前一个问题非常相似。唯一的区别是, 方程式 1 不是以斜坡截击形式出现。我们要么解决 y 将其以斜坡截击形式出现, 要么用截击方式绘制方程式图。要用截击方式查看图形线, 我们将使用后一种方法。

Recall that the $\begin{align*}x-\end{align*}$ intercept can be found by replacing $\begin{align*}y\end{align*}$ with zero and solving for $\begin{align*}x\end{align*}$ :
::回顾 X - 界面可以通过以零替换 Y 和解析 x 找到 :

$\begin{align*}3x+2(0) &= 6\\ 3x &= 6\\ x &=2\end{align*}$
::3x+2(0)=63x=6x=2

Similarly, the $\begin{align*}y-\end{align*}$ intercept is found by replacing $\begin{align*}x\end{align*}$ with zero and solving for $\begin{align*}y\end{align*}$ :
::同样,y- interview 可以通过以零替换 x 并解决 y 找到 y- interview :

$\begin{align*}3(0)+2y &= 6\\ 2y &= 6\\ y &= 3\end{align*}$
::3(0)+2y=62y=6y=3

We have two points, (2, 0) and (0, 3) to plot and graph this line. Equation 2 can be graphed using the $\begin{align*}y-\end{align*}$ intercept and slope, as you have done in problem 1 above.
::我们有两个点, (2, 0) 和 (0, 3) 来绘制和绘制这条线。等式 2 可以使用y- intercept 和斜坡来绘制, 正如您在上文问题 1 中所做的那样。

Now that both lines are graphed , observe that their intersection is the point (4, -3).
::现在两条线都标出图表, 观察它们的交叉点是点( 4, 3) 。

Finally, check this solution by substituting it into each of the two equations.
::最后,检查这一解决方案,将其替换为两个方程式中的每一个方程式。

Equation 1, $\begin{align*}3x+2y =6: \ \ 3(4)+2(-3)=12-6=6 \end{align*}$
::等式 1, 3x+2y=6: 3(4)+2(-3)=12-6=6

Equation 2, $\begin{align*}y = - \frac{1}{2}x-1: \ \ \text{-}3= \text{-}\frac{1}{2}(4)-1 \end{align*}$
::2 y12x-1: - 3=-12(4)- 1等量

Now, let's use technology to solve the system: $\begin{align*}\begin{cases} 2x-3y=10\\ y=\text{-} \frac{2}{3}+4 \end{cases}\end{align*}$
::现在,让我们使用技术解决系统: {2x--3y=10y=23+4

This process may vary somewhat based on the technology you use. All directions here can be applied to the TI-83 or 84 (plus, silver, etc) calculators.
::此过程可能根据您使用的技术而有所不同。这里的所有方向都可以应用到 TI- 83 或 84 (加、银等) 计算器。

The first step is to graph these equations on the calculator. The first equation must be rearranged into slope intercept form to put in the calculator.
::第一步是在计算器上图解这些方程式。第一个方程式必须重新排列为斜坡截停形式, 才能放入计算器。

$\begin{align*}2x-3y &= 10\\ \text{-}3y &= \text{-}2x+10\\ y &=\frac{\text{-}2x+10}{\text{-}3}\\ y &=\frac{2}{3}x-\frac{10}{3}\end{align*}$
::2x-3y=10-3y=2x+10y=2x+10-3y=23x-103

The graph obtained using the calculator should look like this:
::使用计算器获得的图表应该像这个样子:

The first equation, $\begin{align*}y=\frac{2}{3}x-\frac{10}{3}\end{align*}$ , is graphed in $\begin{align*}{\color{blue}\mathbf{blue}}\end{align*}$ . The second equation, $\begin{align*}y=-\frac{2}{3}x+4\end{align*}$ , is graphed in $\begin{align*}{\color{red}\mathbf{red}}\end{align*}$ .
::第一个方程式 y= 23x- 103 以蓝色图解。第二个方程式 y= 23x+ 4 以红色图解。

The solution does not lie on the “grid” and is therefore difficult to observe visually. With technology we can calculate the intersection. If you have a TI-83 or 84, use the CALC menu, select INTERSECT. Then select each line by pressing ENTER on each one. The calculator will give you a “guess.” Press ENTER one more time and the calculator will then calculate the intersection of (5.5, .333...). We can also write this point as $\begin{align*}\left(\frac{11}{2},\frac{1}{3}\right)\end{align*}$ .
::解决方案不存在于“ 电网 ” 上, 因此很难观察。使用技术, 我们可以计算交叉点。如果您有一个 TI- 83 或 84, 请使用 CALC 菜单, 请选择 InterSECT 。然后通过按 ENTER 来选择每条线。计算器会给你一个“ 猜测 ” 。再按 ENTER 一次, 然后计算器将计算( 5. 5 , 333...) 的交叉点。我们也可以将此点写为 (112, 13 ) 。

Check the solution algebraically:
::检查溶液代数 :

Equation 1, $\begin{align*}2x-3y=10: \ \ 2\left(\frac{11}{2}\right)-3\left(\frac{1}{3}\right)=11-1=10 \end{align*}$
::等式1、2x-3y=10:2(112)-3(13)=11-1=10

Equation 2, $\begin{align*}y=- \frac{2}{3}x+4: \ \ \text{-} \frac{2}{3}\left(\frac{11}{2}\right)+4=\text{-}\frac{11}{3}+\frac{12}{3}=\frac{1}{3}\end{align*}$
::2 y23x+4: - 23( 112)+4=- 113+123=13

If you do not have a TI-83 or 84, the commands might be different. Check with your teacher.
::如果您没有 TI-83 或 84, 命令可能不同。请查看您的老师。

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine the value of each of two coins, $\begin{align*}a \text{ and }b.\end{align*}$
::早些时候,你被要求确定两个硬币(a)和(b)的每个硬币的价值。

The system of linear equations represented by this situation is:
::以这种情况为代表的线性方程式系统是:

$\begin{align*}\begin{cases}2a + 4b = 70\\ \ \ a + 5b = 50 \end{cases}\end{align*}$
::{2a+4b=70 a+5b=50

If you plot both of these linear equations on the same graph, you find that the point of intersection is (25, 5). Therefore coin $\begin{align*}a\end{align*}$ has a value of 25 cents and coin $\begin{align*}b\end{align*}$ has a value of 5 cents.
::如果您在同一图中绘制了这两个线性方程式, 就会发现交叉点是( 25, 5) 。因此, 硬币a 的值为 25 美分, 硬币b 的值为 5 美分。

Example 2
::例2

Solve the following system by graphing.
::通过图表绘制解决以下系统。

$\begin{align*}\begin{cases}y = 3x-4\\ y = 2 \end{cases}\end{align*}$
::{y=3x-4y=2

The first line is in slope intercept form and can be graphed accordingly.
::第一行为斜坡截击形式,可按下图绘制。

The second line is a horizontal line through (0, 2).
::第二行是贯穿于(0, 2)的横向线。

The graph of the two equations is shown below.
::下面是两个方程式的图示。

From this graph the solution appears to be (2, 2).
::从这个图表看,解决办法似乎是(2,2)。

Checking this solution in each equation verifies that it is indeed correct.
::在每个方程式中检查此解决方案, 校验是否正确。

Equation 1: $\begin{align*}2=3(2)-4 \end{align*}$
::等式1: 2=3(2)-4

Equation 2: $\begin{align*}2=2 \end{align*}$
::等量2: 2=2

Example 3
::例3

Solve the following system by graphing.
::通过图表绘制解决以下系统。

$\begin{align*}\begin{cases} \ \ 2x-y = \text{-}4\\ 2x+3y =\text{-}12 \end{cases}\end{align*}$
::{2x-y=-42x+3y=-12

Neither of these equations is in slope intercept form. The easiest way to graph them is to find their intercepts as shown in Example B.
::这两种方程式都不是斜坡截击形式,最简单的方式是如例B所示找到拦截。

Equation 1: Let $\begin{align*}y=0\end{align*}$ to find the $\begin{align*}x-\end{align*}$ intercept.
::方程式 1: 让 y=0 找到 x - intercut 。

$\begin{align*} 2x-y &= \text{-}4\\ 2x-0 &= \text{-}4\\ x &= \text{-}2\end{align*}$
::2x-y=-42x-0=-4x=-2

Now let $\begin{align*}x=0\end{align*}$ , to find the $\begin{align*}y-\end{align*}$ intercept.
::现在让 x=0 找到y- interview 。

$\begin{align*} 2x-y &= \text{-}4\\ 2(0)-y &= \text{-}4\\ y &= 4\end{align*}$
::2x-y=-42(0)-y=-4y=4

Now we can use (-2, 0) and (0, 4) to graph the line as shown in the diagram. Using the same process, the intercepts for the second line can be found to be (-6, 0) and (0, -4).
::现在我们可以使用 (-2, 0) 和 (0, 4) 来绘制图表中显示的线条图。使用同样的程序, 第二行的截取量可以被找到 (-6, 0) 和 (0, 4) 。

Now the solution to the system can be observed to be (-3, -2). This solution can be verified algebraically as shown in the first problem.
::现在可以观察到系统的解决办法是 (3 - 2) 。正如第一个问题所示,这个解决办法可以核实代数。

Example 4
::例4

Solve the following system by graphing. Use technology.
::通过图形绘制解决以下系统。使用技术。

$\begin{align*}\begin{cases}5x+y = 10\\ y =\frac{2}{3}x-7 \end{cases}\end{align*}$
::{5x+y=10y=23x-7

The first equation here must be rearranged as $\begin{align*}y=\text{-}5x+10\end{align*}$ before it can be entered into the calculator. The second equation can be entered as is.
::在此第一个方程式必须重新排列为 Y=-5x+10 才能输入计算器。第二个方程式可以原样输入。

Using the calculate menu on the calculator the solution is (3, -5).
::使用计算器上的计算菜单, 解决方案是 (3, 5) 。

Remember to verify this solution algebraically as a way to check your work.
::记住要校验这个代数化的解决方案作为检查你工作的方法

Review
::回顾

Match the system of linear equations to its graph and state the solution.
::将线性方程系统与其图形匹配,并声明解决方案。

$\begin{align*}\begin{cases}3x+2y = \text{-}2\\ \quad \! x-y = \text{-}4 \end{cases}\end{align*}$

::{3x+2y=-2x-y=-4

$\begin{align*}\begin{cases} \ \ 2x-y = 6\\ 2x+3y = 6 \end{cases}\end{align*}$

::{2x-y=62x+3y=6

$\begin{align*}\begin{cases}2x-5y = \text{-}5\\ \ \ x+5y = 5 \end{cases}\end{align*}$

::{2x- 5y=-5 x+5y=5

$\begin{align*}\begin{cases}y = 5x-5\\ y =\text{-}x+1 \end{cases}\end{align*}$

::{y=5x-5y=-x+1

Solve the following linear systems by graphing. Use graph paper and a straightedge to insure accuracy. You are encouraged to verify your answer algebraically.
::通过图形化来解决下列线性系统。使用图形纸和直方来保证准确性。鼓励您核实您的回答代数。

.

$\begin{align*}\begin{cases}y = \text{-} 2x+1\\ x-y = \text{-} 4 \end{cases}\end{align*}$

.

$\begin{align*}\begin{cases}y = \text{-} \frac{2}{3}x+4\\ y = 3x-7 \end{cases}\\ \ \\\end{align*}$

.

$\begin{align*}\begin{cases} y = \text{-} 2x+1\\ x-y =\text{-}4 \end{cases}\end{align*}$

.

$\begin{align*}\begin{cases} 3x+4y = 12\\ \ \ x-4y =4 \end{cases}\end{align*}$

.

$\begin{align*}\begin{cases}7x -2y = \text{-}4\\ y = \text{-}5 \end{cases}\end{align*}$

.

$\begin{align*}\begin{cases}x-2y = \text{-}8\\ x = \text{-}3 \end{cases}\end{align*}$

Solve the following linear systems by graphing using technology. Solutions should be rounded to the nearest hundredth as necessary.
::使用技术图示图解解决下列线性系统。必要时, 解决方案应四舍五入到最接近的百位。

.

$\begin{align*}\begin{cases} y = \frac{3}{7}x+11\\ y = \text{-} \frac{13}{2}x-5 \end{cases}\end{align*}$

.

$\begin{align*}\begin{cases}y = 0.95x -8.3\\ 2x+9y = 23 \end{cases}\end{align*}$

.

$\begin{align*}\begin{cases}15x-y = 22\\ 3x+8y = 15 \end{cases}\end{align*}$

Use the following information to complete exercises 14-17.
::使用以下信息完成14-17演习。

Clara and her brother, Carl, are at the beach for vacation. They want to rent bikes to ride up and down the boardwalk. One rental shop, Bargain Bikes, advertises rates of $5 plus $1.50 per hour. A second shop, Frugal Wheels, advertises a rate of $6 plus $1.25 an hour.
::克拉拉和她的兄弟卡尔正在海滩度假,他们想租自行车上下上下上下上下上下上下上下上下上下上下上下上下上下上下上下上下上下上下上下上下下下上下下下。一个出租商店,Bargain Bikes,广告价为每小时5美元加1.50美元。第二个商店,Frugal 轮,广告价为每小时6美元加1.25美元。

How much does it cost to rent a bike for one hour from each shop? How about 10 hours?
::从每家商店租一个小时的自行车要花多少钱?

Write equations to represent the cost of renting a bike from each shop. Let $\begin{align*}x\end{align*}$ represent the number of hours and $\begin{align*}y\end{align*}$ represent the total cost.
::书写方程式以代表从每个商店租用自行车的费用。让 x 代表小时数, y 代表总费用。

Solve your system to figure out when the cost is the same.
::解决你的系统找出何时成本是相同的。

Clara and Carl want to rent the bikes for about 3 hours. Which shop should they use?
::克拉拉和卡尔想租三小时的自行车

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

使用图形图解的单一解决办法的解决系统

Solving Systems by Graphing ::通过图表绘制的解决系统

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

{ 2 x − y = - 4 2 x + 3 y = - 12 \begin{align*}\begin{cases} \ \ 2x-y = \text{-}4\\ 2x+3y =\text{-}12 \end{cases}\end{align*} ::{2x-y=-42x+3y=-12

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Solving Systems by Graphing
::通过图表绘制的解决系统

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

$\begin{align}\begin{cases} \ \ 2x-y = \text{-}4\\ 2x+3y =\text{-}12 \end{cases}\end{align}$
::{2x-y=-42x+3y=-12

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)