3.4 使用替代物的一次性解决办法的溶解系统

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 使用替代物的单一解决办法的解决系统

  Collapse Expand

  使用替代物的单一解决办法的解决系统

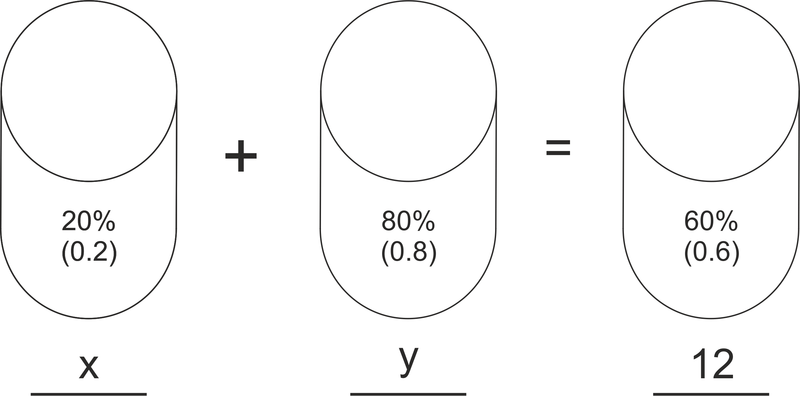
  Rex and Carl are making a mixture in science class. They need to have 12 ounces of a 60% saline solution. To make this solution they have a 20% saline solution and an 80% saline solution. How many ounces of each do they need to make the correct mixture?

  播放段落

  Systems with One Solution Using Substitution
  ::使用替代的一解决方案系统

  播放段落

  In the substitution method we will be looking at the two equations and deciding which variable is easiest to solve for so that we can write one of the equations as $\begin{align*}x=\end{align*}$ or $\begin{align*}y=\end{align*}$ . Next we will replace either the $\begin{align*}x\end{align*}$ or the $\begin{align*}y\end{align*}$ accordingly in the other equation . The result will be a solve-able equation with only one variable.
  ::在替代方法中,我们将查看这两个方程式,并决定最容易解决的变量,以便我们可以将其中一个方程式写成 x= 或 Y= 。接下来我们将在另一个方程式中相应替换 x 或 y。结果将是一个只有一个变量的可解决方程式。

  播放段落

  Let's solve the systems below using substitution.
  ::让我们用替代来解决下面的系统

  1.     

  播放段落

  $$\begin{align*}2x+y &= 12\\ \text{-}3x-5y &= \text{-}11\end{align*}$$
  ::2x+y=12-3x-5y=11

  播放段落

  The first step is to look for a variable that is easy to isolate. In other words, does one of the variables have a coefficient of 1? Yes, that variable is the $\begin{align*}y\end{align*}$ in the first equation. So, start by solving for (isolating)  $\begin{align*}y: \ \ y=\text{-}2x+12.\end{align*}$
  ::第一步是寻找一个容易分离的变量。 换句话说, 变量之一的系数是否为 1 ? 是的, 该变量是第一个方程中的 y。 所以, 从解决( 孤立) y: y= 2x+12 开始 。

  播放段落

  This expression can then be used to replace the $\begin{align*}y\end{align*}$ in the other equation to  solve for $\begin{align*}x:\end{align*}$
  ::此表达式可用于替换其他方程式中的 Y, 以解析 x:

  播放段落

  $$\begin{align*}\text{-}3x-5(\text{-}2x+12) &= \text{-}11\\ \text{-}3x+10x-60 &= \text{-}11\\ 7x-60 &= \text{-}11\\ 7x &= 49\\ x &= 7\end{align*}$$
  ::-3x-5(-2x+12)=-11-3x+10x-60=-117x-60=-117x=-117x=-117x=-49x=7

  播放段落

  Now that we have found $\begin{align*}x\end{align*}$ , we can use this value in our expression to find $\begin{align*}y:\end{align*}$
  ::既然我们找到了 x, 我们可以在表达式中使用这个值来查找 y:

  播放段落

  $$\begin{align*} y &= \text{-}2(7)+12\\ y &= \text{-}14+12\\ y &= \text{-}2\end{align*}$$
  ::y=-2(7)+12y=-14+12y=-2

  播放段落

  Recall that the solution to a linear system is a point in the coordinate plane where the two lines intersect. Therefore , our answer should be written as a point: (7, -2). You can check your answer by substituting this point into both equations to make sure that it satisfies them:
  ::回顾线性系统的解决方案是坐标平面上两条线交叉的一个点。 因此, 我们的答案应该写成一个点 : (7, - 2) 。 您可以将这个点替换成两个方程式来检查答案, 以确保它满足 :

  $$\begin{align*}2(7)+ \text{-}2 &= 14-2=12\\ \text{-}3(7)-5(\text{-}2) &= \text{-}21+10 = \text{-}11 \end{align*}$$

  2.    

  播放段落

  $$\begin{align*}2x+3y &= 13\\ x+5y &= \text{-}4\end{align*}$$
  ::2x+3y=13x+5y=-4

  播放段落

  In the last problem , $\begin{align*}y\end{align*}$ was the easiest variable to isolate. Is that the case here? No, this time, $\begin{align*}x\end{align*}$ is the variable with a coefficient of 1. It is easy to fall into the habit of always isolating $\begin{align*}y\end{align*}$ since you have done it so much to write equation in slope-intercept form . Try to avoid this and look at each system to see which variable is easiest to isolate. Doing so will help reduce your work.
  ::在最后一个问题中, y 是最容易分离的变量 。 情况是这样吗 ? 不, 这次, x 是系数为 1 的变量 。 由于您已经做了很多工作, 用斜坡界面写了方程式。 尝试避免这一点, 并查看每个系统 看看哪个变量最容易分离 。 这样做有助于减少您的工作 。

  播放段落

  Solving the second equation for $\begin{align*}x\end{align*}$ gives: $\begin{align*}x = \text{-}5y-4.\end{align*}$
  ::解析 x 的第二个方程式时给出: x=-5y-4 。

  播放段落

  This expression can be used to replace the $\begin{align*}x\end{align*}$ in the other equation and solve for $\begin{align*}y:\end{align*}$
  ::此表达式可用于替换其他方程式中的 x, 并解决 y:

  播放段落

  $$\begin{align*}2(\text{-}5y-4)+3y &= 13\\ \text{-}10y-8+3y &= 13\\ \text{-}7y-8 &= 13\\ \text{-}7y &= 21\\ y &= \text{-}3\end{align*}$$
  ::2(5-5y-4)+3y=13-10y-8+3y=13-7y-8=13-7y=13-7y=21y=3)

  播放段落

  Now that we have found $\begin{align*}y\end{align*}$ , we can use this value in our expression to find $\begin{align*}x\end{align*}$ :
  ::既然我们找到了y, 我们可以在表达式中使用这个值来找到x:

  播放段落

  $$\begin{align*}x &= \text{-}5(\text{-}3)-4\\ x &= 15-4\\ x &= 11\end{align*}$$
  ::x=5(-3)-4x=15-4x=11

  播放段落

  So, the solution to this system is (11, -3). Don’t forget to check your answer:
  ::所以,这个制度的解决方案是(11, -3)。 不要忘了检查你的答案:

  $$\begin{align*}2(11)+3(\text{-}3) &= 22-9=13\\ 11+5(\text{-}3) &= 11-15= \text{-}4 \end{align*}$$

  3.     

  播放段落

  $$\begin{align*}4x+3y &=4\\ 6x-2y &= 19\end{align*}$$
  ::4x+3y=46x-2yy=19

  播放段落

  In this case, none of the variables have a coefficient of 1. So  l et’s solve for the $\begin{align*}x\end{align*}$ in equation 1:
  ::在此情况下,没有一个变量的系数为1。 所以让我们解决方程式1中的 x 问题:

  播放段落

  $$\begin{align*}4x &= \text{-}3y +4\\ x &= \text{-} \frac{3}{4}y+1\end{align*}$$
  ::4x=-3y+4x=-34y+1

  播放段落

  Now this expression can be used to replace the $\begin{align*}x\end{align*}$ in the other equation and solve for $\begin{align*}y:\end{align*}$
  ::此表达式可用于替换其他方程式中的 x, 并解决 y:

  播放段落

  $$\begin{align*}6 \left(\text{-} \frac{3}{4}y+1 \right)-2y &= 19\\ \text{-} \frac{18}{4}y+6-2y &= 19\\ \text{-} \frac{9}{2}y- \frac{4}{2}y &= 13\\ \text{-} \frac{13}{2}y &= 13\\ \left(\text{-}\frac{2}{13} \right)\left( \text{-} \frac{13}{2} \right)y &= 13\left( \text{-} \frac{2}{13} \right)\\ y &= \text{-}2\end{align*}$$
  ::6(-34y+1)-2y=19-184y+6-2y=19-92y-42y=13-132y=13(-213)(-132)(-132)y=13(-213)y=2

  播放段落

  Now that we have found $\begin{align*}y\end{align*}$ , we can use this value in our expression find $\begin{align*}x:\end{align*}$
  ::既然我们找到了y, 我们可以在表达式查找 x 中使用这个值 :

  播放段落

  $$\begin{align*}x &= \left(- \frac{3}{4} \right)(-2)+1\\ x &= \frac{6}{4}+1 \\ x &= \frac{3}{2}+\frac{2}{2}\\ x &= \frac{5}{2}\end{align*}$$
  ::x=(- 34)(-2)+1x=64+1x=32+22x=52

  播放段落

  So, the solution is $\begin{align*}\left( \frac{5}{2}, \text{-}2 \right)\end{align*}$ . Check your answer:
  ::所以,答案是 (52,-2) 。请检查您的答案 :

  $$\begin{align*}4\left(\frac{5}{2}\right)+3(\text{-}2) &= 10-6=4\\ 6\left(\frac{5}{2}\right)-2(\text{-}2) &= 15+4 =19 \end{align*}$$

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find the number of ounces of each of two concentrations of solution Rex and Carl need to make a particular mixture.
  ::早些时候,你被要求 找到两个浓度的溶液 每一盎司的数量 雷克斯和卡尔需要制造 一种特定的混合物。

  播放段落

  Let’s try to make the word problem easier by organizing the  information into a “picture” equation as shown below:
  ::让我们把信息组织成下文所示的“图象”等式,

  

  播放段落

  In this picture, we can see that they will be mixing $\begin{align*}x\end{align*}$ ounces of the 20% solution with $\begin{align*}y\end{align*}$ ounces of the 80% solution to get 12 ounces of the 60% solution. The two equations are thus:
  ::在这张图中,我们可以看到它们将把20%的溶液的x盎司与80%的溶液的y盎司混合,以获得60%的溶液的12盎司。

  播放段落

  $$\begin{align*}0.2x+0.8y &= 0.6(12)\\ x+y &= 12\end{align*}$$
  ::0.2x+0.8.8y=0.6(12)x+y=12

  播放段落

  Now we can solve the system using substitution. Solve for $\begin{align*}y\end{align*}$ in the second equation to get  $\begin{align*}y = 12-x.\end{align*}$
  ::现在我们可以用替换解决系统。 在第二个方程式中为 y 解决 y , 以获得 Y= 12 - x 。

  播放段落

  Now, substitute and solve in the first equation:
  ::现在,第一个方程式的替代和解答:

  播放段落

  $$\begin{align*}0.2x+0.8(12-x) &= 0.6(12)\\ 0.2x+9.6-0.8x &= 7.2\\ \text{-}0.6x &= \text{-}2.4\\ x &= 4\end{align*}$$
  ::0ux+0.8(12-x)=0.6(12)0.02x+9.6-0.8x=7.2-0.6x=-2.4x=4

  播放段落

  Now find $\begin{align*}y\end{align*}$ :
  ::现在找到 y :

  播放段落

  $$\begin{align*}y &= 12-x\\ y &= 12-4\\ y &= 8\end{align*}$$
  ::y=12-xy=12-4y=8

  播放段落

  Therefore, Rex and Carl need 4 ounces of the 20% saline solution and 8 ounces of the 80% saline solution to make the correct mixture.
  ::因此,Rex和Carl需要 20%盐碱溶液的4盎司 80%盐溶液的8盎司 才能做出正确的混合物

  播放段落

  Solve the following systems using the substitution method.
  ::使用替代方法解决以下系统。

  播放段落

  Example 2
  ::例2

  播放段落

  $$\begin{align*}3x+4y &= \text{-}13\\ x &=\text{-}2y-9\end{align*}$$
  ::3x+4y=13x=-2y-9

  播放段落

  In this problem, the second equation is already solved for $\begin{align*}x,\end{align*}$ so we can use that in the first equation to find $\begin{align*}y\end{align*}$ :
  ::在这个问题中,第二个方程式已经为 x 解决了, 所以我们可以在第一个方程式中使用它来找到 y:

  播放段落

  $$\begin{align*}3(\text{-}2y-9)+4y &= \text{-}13\\ \text{-}6y-27+4y &= \text{-}13\\ \text{-}2y-27 &= \text{-}13\\ \text{-}2y &= 14\\ y &= \text{-}7\end{align*}$$
  ::3(3-2y-9)+4y=-13-6y-27+4y=-13-2y-27=-13-2y-y=-13-2y=-13-2y=14y=-7)

  播放段落

  Now we can find $\begin{align*}x\end{align*}$ :
  ::现在我们可以找到x:

  播放段落

  $$\begin{align*}x &= \text{-}2(\text{-}7)-9\\ x &= 14-9\\ x &= 5\end{align*}$$
  ::x=-2(-7)-9x=14-9x=5

  播放段落

  Therefore the solution is (5, -7).
  ::因此,解决办法是(5,7) 。

  播放段落

  Example 3
  ::例3

  播放段落

  $$\begin{align*}\text{-}2x-5y &= \text{-}39\\ x+3y &=24\end{align*}$$
  ::-2x--5y=-39x+3y=24

  播放段落

  This time the $\begin{align*}x\end{align*}$ in the second equation is the easiest variable to isolate: $\begin{align*}x=-3y+24.\end{align*}$  Let’s use this in the first expression to find $\begin{align*}y\end{align*}$ :
  ::这一次,第二个方程式中的 x 是最容易分离的变量 : x3y+24。 让我们在第一个表达式中使用它来查找 y :

  播放段落

  $$\begin{align*}\text{-}2(\text{-}3y+24)-5y &= \text{-}39\\ 6y-48-5y &= \text{-}39\\ y-48 &= \text{-}39\\ y &=9\end{align*}$$
  :2-3y+24)-5y=-396y-48-5y=-39y-48=-39y=-39y=9

  播放段落

  Now we can find $\begin{align*}x\end{align*}$ :
  ::现在我们可以找到x:

  播放段落

  $$\begin{align*}x &= \text{-}3(9)+24\\ x &= \text{-}27+24\\ x &= \text{-}3\end{align*}$$
  ::x=-3(9)+24x=-27+24x=-3

  播放段落

  Therefore the solution is (-3, 9).
  ::因此,解决办法是(-3,9)。

  播放段落

  Example 4
  ::例4

  播放段落

  $$\begin{align*}y &= \frac{1}{2}x-21\\ y &= \text{-}2x+9\end{align*}$$
  ::y=12x-21y=-2x+9

  播放段落

  In this case, both equations are equal to $\begin{align*}y\end{align*}$ . Since $\begin{align*}y=y\end{align*}$ , by the Reflexive Property of Equality, we can set the right hand sides of the equations be equal too. This is still a substitution problem; it just looks a little different.
  ::在这种情况下,两个方程式都与y等同。y=y,根据“平等弹性属性 ” , 我们可以将方程式的右侧也设置为相等。 这仍然是一个替代问题; 它看起来有点不同了 。

  播放段落

  $$\begin{align*}\frac{1}{2}x-21 &= \text{-}2x+9\\ 2 \left( \frac{1}{2}x-21 \right) &= 2(\text{-}2x+9)\\ x-42 &= \text{-}4x+18\\ 5x &= 60\\ x &= 12\end{align*}$$
  ::12-21=-2-2x+92(12x-21)=2(-2x+9)x-42=-4x+185x=60x=12

  播放段落

  Now we can find $\begin{align*}y\end{align*}$ :
  ::现在我们可以找到y:

  播放段落

  $$\begin{align*}y &= \frac{1}{2}(12)-21 \qquad \quad \quad y = \text{-}2(12)+9\\ y &= 6-21 \qquad \quad \text{or} \qquad y = \text{-}24+9\\ y &= \text{-}15 \qquad \qquad \qquad \quad y = \text{-}15\end{align*}$$
  ::y=12(12)-21y=-2(12)+9y=6-21y=24+9y=15

  播放段落

  Therefore, the solution is (12, -15).
  ::因此,解决办法是(12,15)。

  播放段落

  Review
  ::回顾

  播放段落

  Solve the following systems using substitution. Remember to check your answers.
  ::使用替代解决以下系统。 记住检查您的答案 。

  播放段落
  1. .   $\begin{align*}\begin{cases} x+3y= \text{-}1\\ 2x+9y= 7 \end{cases}\end{align*}$
     ::。 {x+3y=-12x+9y=7

  播放段落
  2. .a $\begin{align*}\ \\ \begin{cases} 5x+2y= 0\\ y= x-7 \end{cases}\\ \ \\\end{align*}$  
     ::a. a. {5x+2y=0y=x-7

  播放段落
  3. . $\begin{align*}\begin{cases} 5x+2y= 0\\ y= x-7 \end{cases}\end{align*}$  
     ::. 5x+2y=0y=x-7

  播放段落
  4. . $\begin{align*}\ \\ \begin{cases} 2x-5y= 21\\ x= \text{-}6y +2 \end{cases}\\ \ \\\end{align*}$
     ::。 {2x-5y=21x=-6y+2

  播放段落
  5. . $\begin{align*}\begin{cases} y= x+3\\ y= 2x-1 \end{cases}\end{align*}$  
     ::. y=x+3y=2x-1

  播放段落
  6. . $\begin{align*}\ \\ \begin{cases}x+6y= 1\\ \text{-}2x-11y= \text{-}4 \end{cases}\\ \ \\\end{align*}$  
     ::。 {x+6y=1-2x-11y=4

  播放段落
  7. .   $\begin{align*}\begin{cases}2x+y= 18\\ \text{-}3x+11y= \text{-}27 \end{cases}\end{align*}$
     ::. {2x+y=18-3x+11y=27

  播放段落
  8. . $\begin{align*}\ \\ \begin{cases}2x+3y= 5\\ 5x+7y= 8 \end{cases}\\ \ \\\end{align*}$  
     ::。 {2x+3y=55x+7y=8

  播放段落
  9. . $\begin{align*}\begin{cases}\text{-}7x+2y= 9\\ 5x-3y= 3 \end{cases}\end{align*}$  
     ::{-7x+2y=95x-3y=3

  播放段落
  10. . $\begin{align*}\ \\ \begin{cases}2x-6y= \text{-}16\\ \text{-}6x+10y= 8 \end{cases}\\ \ \\\end{align*}$  
      ::。 {2x-6y=-16-6x+10y=8

  播放段落
  11. . $\begin{align*}\begin{cases}2x-3y= \text{-}3\\ 8x+6y= 12 \end{cases}\end{align*}$  
      ::. {2x--3y=- 38x+6y=12

  播放段落
  12. . $\begin{align*}\ \\ \begin{cases}5x+y= \text{-}3\\ y= 15x+9\end{cases}\\ \ \\\end{align*}$  
      ::。 {5x+y=-3y=15x+9

  播放段落

  Set up and solve a system of linear equations to answer each of the following word problems.
  ::设置并解决一个线性方程式系统, 以回答以下每个字的问题 。

  播放段落
  13. Alicia and Sarah are at the supermarket. Alicia wants to get peanuts from the bulk food bins and Sarah wants to get almonds. The almonds cost $6.50 per pound and the peanuts cost $3.50 per pound. Together they buy 1.5 pounds of nuts. If the total cost is $6.75, how much did each girl get? Set up a system to solve using substitution.
      ::Alicia和Sarah在超市。Alicia想从散装食品中买花生,Sarah想买杏仁。杏仁每磅6.50美元,花生每磅3.50美元。他们一起买1.5磅坚果。如果总成本是6.75美元,每个女孩能得到多少?建立一个系统,用替代方法解决问题。
  播放段落
  14. Marcus goes to the department store to buy some new clothes. He sees a sale on t-shirts ($5.25) and shorts ($7.50). Marcus buys seven items and his total, before sales tax, is $43.50. How many of each item did he buy?
      ::马库斯去百货商店买些新衣服。他看到一件T恤(5.25美元)和短裤(7.50美元)的销售。马库斯买了七件,在销售税之前,他的总额是43.50美元。他每件都买了多少件?
  播放段落
  15. Jillian is selling tickets for the school play. Student tickets are $3 and adult tickets are $5. If 830 people buy tickets and the total revenue is $3104, how many students attended the play?
      ::吉莉安在卖学校游戏的票。学生票是3美元,成人票是5美元。如果830人买票,总收入是3104美元,有多少学生参加了这场比赛?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。