课程： 5.17 矢量乘Scalar的乘数

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节由 Scalar 组合的矢量

折叠展开
由 Scalar 组合的矢量
While at summer camp, you are enjoying a tug of war with your friends. You are on one side of the rope, pulling with a force of 200 N. The vector for this force can be represented like this:
::在夏令营期间,你正享受着与朋友的拔河战争。你站在绳索的一边,用200N的力量拉着。这支力量的矢量可以像这样表示:

You decide to really go for the win and pull as hard as you possibly can. As it turns out, you are pulling with twice the force you were before. Do you know how you can represent the vector for this?
::您真的决定去争取胜利, 并尽你最大的努力拉。事实证明, 您的拉力是您之前的两倍。您知道如何代表矢量吗 ?

Multiplying Vectors and Scalars
::乘向量和Scalars

In working with vectors there are two kinds of quantities employed. The first is the vector, a quantity that has both magnitude and direction. The second quantity is a scalar. Scalars are just numbers. The magnitude of a vector is a scalar quantity. A vector can be multiplied by a real number. This real number is called a scalar . The product of a vector $\begin{aligned} \vec{a} \end{aligned}$ and a scalar $\begin{aligned} k \end{aligned}$ is a vector, written $\begin{aligned} \vec{k a} \end{aligned}$ . It has the same direction as $\begin{aligned} \vec{a} \end{aligned}$ with a magnitude of $\begin{aligned} k | \vec{a} | \end{aligned}$ if $\begin{aligned} k > 0 \end{aligned}$ . If $\begin{aligned} k < 0 \end{aligned}$ , the vector has the opposite direction of $\begin{aligned} \vec{a} \end{aligned}$ and a magnitude of $\begin{aligned} k | \vec{a} | \end{aligned}$ .
::与矢量一起工作时使用两种数量。第一类是矢量, 其数量既具有大小又具有方向。第二类是标量。星标只是数字。矢量的大小是标量。矢量可以乘以一个实际数字。这个实际数字叫做标量。矢量 a 和 scalar k 的产物是矢量, 写入 kaQ 。其方向与 a 相同, 如果 k > 0 , 其大小为 ka 和 k Q 。如果 k < 0 , 该矢量的向量与 a 和 k Q 的相反方向是。

Finding Vectors
::查找矢量

1. Find the current vector for wind velocity.
::1. 为风速寻找当前矢量。

The speed of the wind before a hurricane arrived was 20 mph from the SSE ( $\begin{aligned} N {22.5}^{\circ} W \end{aligned}$ ). It quadrupled when the hurricane arrived. What is the current vector for wind velocity?
::飓风到来前的风速是SSE(N22.5W)的20米。飓风到来时风速翻了四倍。风速的当前矢量是什么?

The wind is coming now at 80 mph from the same direction.
::风从同一方向以80英里的速度吹来

2. A sailboat was traveling at 15 knots due north. After realizing he had overshot his destination, the captain turned the boat around and began traveling twice as fast due south. What is the current velocity vector of the ship?
::2. 一艘帆船在15海里处向北行驶,在意识到他已超速抵达目的地后,船长转过船头,开始以南飞速两倍的速度行驶。

The ship is traveling at 30 knots in the opposite direction.
::船在30海里处向相反方向行驶

If the vector is expressed in coordinates with the starting end of the vector at the origin, this is called standard form. To perform a scalar multiplication , we multiply our scalar by both the coordinates of our vector. The word scalar comes from “scale.” Multiplying by a scalar just makes the vectors longer or shorter, but doesn't change their direction.
::如果矢量在源头矢量的起始端以坐标表示,则这被称为标准格式。要执行一个天平乘法,我们用矢量的坐标将天平乘以我们的天平乘法。“天平”一词来自“尺度 ” 。以天平乘以天平使矢量变长或变短,但不会改变方向。

Determining the Representation of a Vector
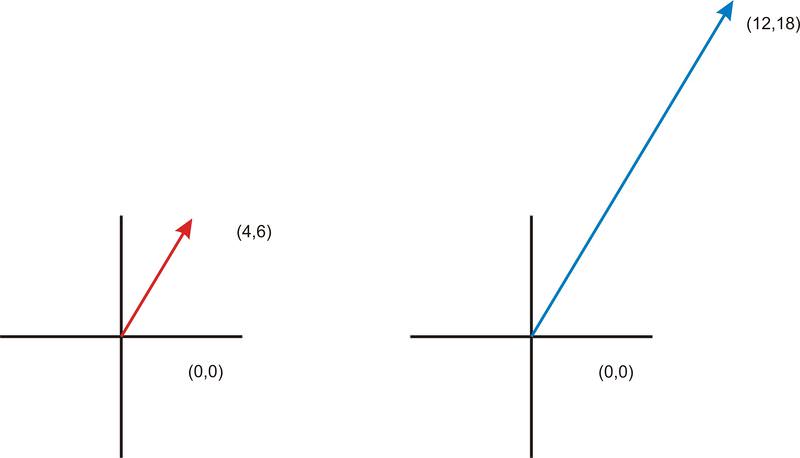
::确定矢量代表

1. Consider the vector from the origin to (4, 6). What would the representation of a vector that had three times the magnitude be?
::1. 将矢量从来源到(4,6)考虑为(4,6),如果矢量是其规模的三倍,那么矢量的表示方式是什么?

Here $\begin{aligned} k = 3 \end{aligned}$ and $\begin{aligned} \vec{v} \end{aligned}$ is the directed segment from (0,0) to (4, 6).
::这里 k=3 和 v 是从( 0,0) 到( 4, 6) 的定向段。

Multiply each of the components in the vector by 3.
::乘以矢量中的每个组件乘以 3 。

$\begin{aligned} \vec{k v} & = (0, 0) t o (12, 18) \end{aligned}$

::kv( 0, 0) 至 (12, 18)

The new coordinates of the directed segment are (0, 0), (12, 18).
::定向段的新坐标为(0,0),(12,18)。

Examples
::实例

Example 1
::例1

Earlier, you were asked to represent a vector.
::早些时候,你被要求代表一个矢量。

Since the original vector looked like this:
::原矢量看起来是这样的:

The new vector is equal to 2 times the old vector. As we found in this section, multiplication of a vector by a scalar doesn't change the direction of the vector, only its magnitude. Therefore, the new vector looks like this:
::新矢量等于旧矢量的2倍。正如我们在本节中发现的那样, 矢量的乘法不会改变矢量的方向, 只改变其大小。因此, 新矢量看起来是这样的:

Its length is twice the length of the original vector, and its direction is unchanged.
::其长度是原始矢量长度的两倍,其方向不变。

Example 2
::例2

Find the resulting ordered pair that represents $\begin{aligned} \vec{a} \end{aligned}$ in each equation if you are given $\begin{aligned} \vec{b} = (0, 0) t o (5, 4) \end{aligned}$ and $\begin{aligned} \vec{a} = 2 \vec{b} \end{aligned}$ .
::如果给您 b(0,0) 至 (5,4) 和 a2b, 则在每一个方程中查找相应的定购对。

$\begin{aligned} 2 \vec{b} = 2 ⟨ 5, 4 ⟩ = ⟨ 10, 8 ⟩ = 10 \hat{i} + 8 \hat{j} \end{aligned}$
::2,2,5,4,10,8,10i,8j

Example 3
::例3

Find the resulting ordered pair that represents $\begin{aligned} \vec{a} \end{aligned}$ in each equation if you are given $\begin{aligned} \vec{b} = (0, 0) t o (5, 4) \end{aligned}$ and $\begin{aligned} \vec{a} = - \frac{1}{2} \vec{b} \end{aligned}$ .
::如果给您 b( 0) 至 ( 5, 4) 和 a 12b , 则在每一方程中查找相应的定购对数, 表示 a( a) 。

$\begin{aligned} - \frac{1}{2} \vec{c} = - \frac{1}{2} ⟨ - 3, 7 ⟩ = ⟨ 1.5, - 3.5 ⟩ = 1.5 \hat{i} - 3.5 \hat{j} \end{aligned}$
::- 12 12 3 7 1.5,- 3.5 5 i 5 j

Example 4
::例4

Find the resulting ordered pair that represents $\begin{aligned} \vec{a} \end{aligned}$ in each equation if you are given $\begin{aligned} \vec{b} = (0, 0) t o (5, 4) \end{aligned}$ and $\begin{aligned} \vec{a} = 0.6 \vec{b} \end{aligned}$ .
::如果给您 b( 0,0) 至 (5,4) 和 a0. 6b , 则查找每个方程中代表 a( a) 的定购对。

$\begin{aligned} 0.6 \vec{b} = 0.6 ⟨ 5, 4 ⟩ = ⟨ 3, 2.4 ⟩ = 3 \hat{i} + 2.4 \hat{j} \end{aligned}$
::0.6b 0.65,43,2.432.4j4j

Review
::回顾

$\begin{aligned} \vec{a} \end{aligned}$ is in standard position with terminal point (1, 5) and $\begin{aligned} \vec{b} \end{aligned}$ is in standard position with terminal point (4, 2).
::a 处于标准位置,有终点(1,5),b 处于标准位置,有终点(4,2)。

Find the coordinates of the terminal point of $\begin{aligned} 2 \vec{a} \end{aligned}$ .
::查找 2a 终点点的坐标。

Find the coordinates of the terminal point of $\begin{aligned} \frac{1}{2} \vec{b} \end{aligned}$ .
::查找12b的终点点的坐标。

Find the coordinates of the terminal point of $\begin{aligned} 6 \vec{a} \end{aligned}$ .
::查找6a终点点的坐标。

$\begin{aligned} \vec{c} \end{aligned}$ is in standard position with terminal point (4, 3) and $\begin{aligned} \vec{d} \end{aligned}$ is in standard position with terminal point (2, 2).
::c 处于标准位置,有终点点(4,3),d 处于标准位置,有终点点(2,2))。

Find the coordinates of the terminal point of $\begin{aligned} 3 \vec{c} + 2 \vec{d} \end{aligned}$ .
::查找 3c2d的终点点的坐标。

Find the coordinates of the terminal point of $\begin{aligned} 4 \vec{c} - 0.3 \vec{d} \end{aligned}$ .
::查找 4c0.3d的终点点的坐标。

Find the coordinates of the terminal point of $\begin{aligned} \vec{c} - 3 \vec{d} \end{aligned}$ .
::查找 c3d的终点点的坐标。

$\begin{aligned} \vec{e} \end{aligned}$ is in standard position with terminal point (3, 2) and $\begin{aligned} \vec{f} \end{aligned}$ is in standard position with terminal point (-1, 2).
::e处于标准位置,终点点(3,2)和F处于标准位置,终点点(1,2)为标准位置。

Find the coordinates of the terminal point of $\begin{aligned} 4 \vec{e} + 5 \vec{f} \end{aligned}$ .
::查找 4e5f的终点点的坐标。

Find the coordinates of the terminal point of $\begin{aligned} 3 \vec{e} - 3 \vec{f} \end{aligned}$ .
::查找 3e3f的终点点的坐标。

Find the coordinates of the terminal point of $\begin{aligned} 5 \vec{e} + \frac{3}{4} \vec{f} \end{aligned}$ .
::查找 5e34f的终点点的坐标。

$\begin{aligned} \vec{g} \end{aligned}$ is in standard position with terminal point (5, 5) and $\begin{aligned} \vec{h} \end{aligned}$ is in standard position with terminal point (4, 2).
::g 处于标准位置,端点(5,5),h 处于标准位置,端点(4,2),端点(4,2)

Find the coordinates of the terminal point of $\begin{aligned} \vec{g} + 4 \vec{h} \end{aligned}$ .
::查找 g4h的终点点的坐标。

Find the coordinates of the terminal point of $\begin{aligned} 5 \vec{g} - 2 \vec{h} \end{aligned}$ .
::查找5g2h的终点点的坐标。

Find the coordinates of the terminal point of $\begin{aligned} 2 \vec{g} - 3 \vec{h} \end{aligned}$ .
::查找 2g3h的终点点的坐标。

$\begin{aligned} \vec{i} \end{aligned}$ is in standard position with terminal point (1, 5) and $\begin{aligned} \vec{j} \end{aligned}$ is in standard position with terminal point (-3, 1).
::i 处于标准位置,有终点(1,5),j 处于标准位置,有终点(-3,1)。

Find the coordinates of the terminal point of $\begin{aligned} 3 \vec{i} - \vec{j} \end{aligned}$ .
::查找 3ij的终点点的坐标。

Find the coordinates of the terminal point of $\begin{aligned} 0.5 \vec{i} - 0.6 \vec{j} \end{aligned}$ .
::查找0.5i0.6j的终点点的坐标。

Find the coordinates of the terminal point of $\begin{aligned} 6 \vec{i} + 1.2 \vec{j} \end{aligned}$ .
::查找6i1.2j的终点点的坐标。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

由 Scalar 组合的矢量

Multiplying Vectors and Scalars ::乘向量和Scalars

Finding Vectors ::查找矢量

Determining the Representation of a Vector ::确定矢量代表

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Multiplying Vectors and Scalars
::乘向量和Scalars

Finding Vectors
::查找矢量

Determining the Representation of a Vector
::确定矢量代表

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)