5.18 矢量和斜坡的翻译

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 矢量和斜坡的翻译

  Collapse Expand

  矢量和斜坡的翻译

  播放段落

  You and your friends are at a ski weekend for your school. While skiing, you go down a hill that is rather steep. You decide to use a vector to represent your motion from the top of the hill going down. Counting the top of the hill as the origin, you ski down a slope and measure how far your "x" and "y" positions have changed. As it turns out, you can represent this displacement with the vector $\begin{align*}(12, -256)\end{align*}$ . Can you calculate the incline (slope) of the hill you came down?
  ::你和你的朋友们在周末上学滑雪。滑雪时,你们下山时要跳得相当陡峭。你们决定用矢量来代表你们从山顶上往下运动。把山顶计为起源,滑下坡坡,测量你们的“x”和“y”位置变化了多少。结果显示,你们可以用矢量(12,-256)来代表这种迁移(12,2-256),你能计算下山的内线吗?

  播放段落

  Translating Vectors and Slopes
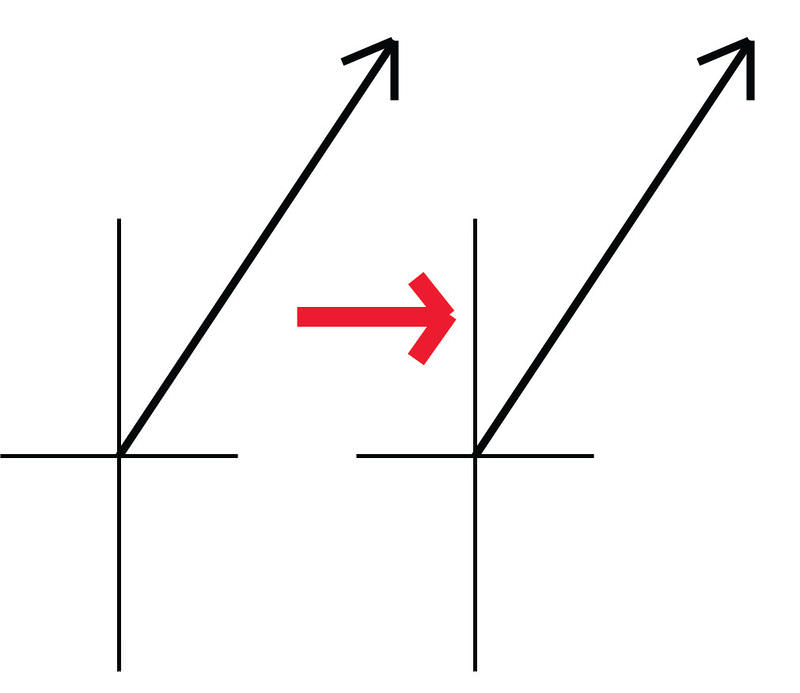
  ::传导矢量和斯隆

  播放段落

  Vectors with the same magnitude and direction are equal. This means that the same ordered pair could represent many different vectors.
  ::向量和方向相同的向量相等。 这意味着同一对定购的向量可以代表许多不同的向量。

  播放段落

  For instance, the ordered pair (4, 8) can represent a vector in standard position where the initial point is at the origin and the terminal point is at (4, 8). This vector could be thought of as the of a horizontal vector with a magnitude or 4 units and a vertical vector with a magnitude of 8 units. Therefore, any vector with a horizontal component of 4 and vertical component of 8 could also be represented by the ordered pair (4, 8).
  ::例如,定单对(4,8)可以代表标准位置的矢量,初始点位于起始点,终点点位于(4,8),该矢量可被视为具有星度或4个单位的水平矢量,垂直矢量为8个单位的垂直矢量,因此,任何具有水平组成部分为4和垂直组成部分为8的矢量也可以由定单对(4,8)代表。

  播放段落

  If you think back to Algebra, you know that the slope of a line is the change in $\begin{align*}y\end{align*}$ over the change in $\begin{align*}x\end{align*}$ , or the vertical change over the horizontal change.
  ::如果您回想到代数, 你知道线的斜坡是 y 相对于 x 的变化的变化, 或者水平变化的垂直变化 。

  播放段落

  Let's take a look at some problems that involve translating vectors and slopes. 
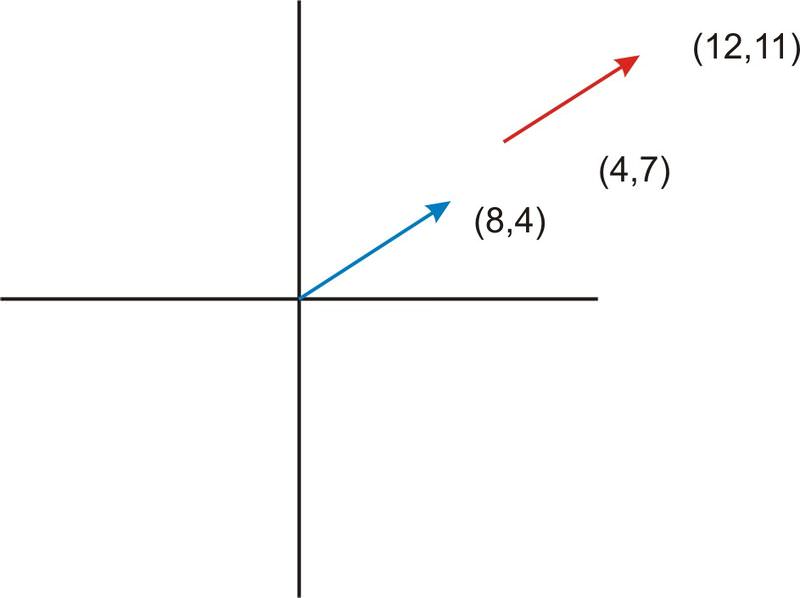
  ::让我们来看看有些问题 涉及到传导矢量和斜坡的翻译

  播放段落

  1. Consider the vector from (4, 7) to (12, 11). What would the representation of a vector that had 2.5 times the magnitude be?
  ::1. 将矢量从(4,7)到(12,11)考虑进去。

  播放段落

  Here, $\begin{align*}k = 2.5\end{align*}$ and $\begin{align*}\vec{v} =\end{align*}$ the directed segment from (4, 7) to (12, 11).
  ::在这里, k=2.5 和 v 方向段从 (4, 7) 到 (12, 11) 。

  播放段落

  Mathematically, two vectors are equal if their direction and magnitude are the same. The positions of the vectors do not matter. This means that if we have a vector that is not in standard position, we can translate it to the origin. The initial point of $\begin{align*}\vec{v}\end{align*}$ is (4, 7). In order to translate this to the origin, we would need to add (-4, -7) to both the initial and terminal points of the vector.
  ::从数学角度讲,如果两个矢量的方向和大小相同,则两个矢量是相等的。矢量的位置无关紧要。这意味着如果我们的矢量不处于标准位置,我们可以将其转换为源。 v的起始点是 (4, 7) 。为了将其转换为源,我们需要在矢量的初始点和终端点上添加( 4, 7) 。

  播放段落

  Initial point: $\begin{align*}(4, 7) + (-4, -7) = (0,0)\end{align*}$
  ::初始点: (4,7)+(-4,7)=(0,0)

  播放段落

  Terminal point: $\begin{align*}(12, 11) + (-4, -7) = (8, 4)\end{align*}$
  ::终点: (12,11)+(-4,-7)=(8,4)

  

  播放段落

  Now, to calculate $\begin{align*}\vec{kv}\end{align*}$ :
  ::现在,要计算 kv :

  播放段落

  $$\begin{align*}\vec{kv} & = (2.5(8), 2.5(4)) \\ \vec{kv} & = (20,10)\end{align*}$$
  ::kv( 2.5(8), 2.5(4))kv( 20, 10)

  播放段落

  The new coordinates of the directed segment are (0, 0) and (20, 10). To translate this back to our original terminal point:
  ::定向段的新坐标是(0,0)和(20,10)。

  播放段落

  Initial point: $\begin{align*}(0, 0) + (4, 7) = (4, 7) \end{align*}$
  ::初始点: (0,0)+(4,7)=(4,7)

  播放段落

  Terminal point: $\begin{align*}(20, 10) + (4, 7) = (24, 17)\end{align*}$
  ::终点: (20,10)+(4,7)=(24,17)

  播放段落

  The new coordinates of the directed segment are (4, 7) and (24, 17).
  ::指示段的新坐标是(4,7)和(24,17)。

  播放段落

  2. What is the slope of a vector starting from the origin with terminal coordinates (5 , 7)?
  ::2. 矢量的斜坡是什么,从源头起,带有终端坐标(5,7)?

  播放段落

  Since the slope is defined as the change in "y" divided by the change in "x", we can find the slope of this vector:
  ::由于斜坡的定义是“y”的变动除以“x”的变动,我们可以找到该矢量的斜坡:

  播放段落

  $$\begin{align*} \frac{\Delta y}{\Delta x} = \frac{7 - 0}{5 - 0} = \frac{7}{5} = 1.4 \end{align*}$$
  ::yx=7-05-0=75=1.4

  播放段落

  3. Find the new coordinates of the vectors
  ::3. 寻找矢量的新坐标

  播放段落

  A vector starts at the origin and has terminal coordinates (11 , 17). What would the new coordinates of the tail and tip of the vector be if the vector were shifted 15 units along the "x" axis?
  ::矢量从源点开始,有终端坐标(11,17)。如果矢量沿“x”轴移动15个单位,则矢量尾部和端部的新坐标是什么?

  播放段落

  The vector maintains the same orientation in space, it is just moved down the "x" axis. Therefore, only the "x" coordinates of the vector's tail and tip change.
  ::矢量在空间中保持相同的方向, 它只是移到“ x” 轴下。 因此, 只有矢量尾部和尾部变化的“ x” 坐标 。

  

  播放段落

  So the new coordinates of the tail of the vector are:
  ::因此矢量尾部的新坐标是:

  $$\begin{align*} (0 + 15, 0) = (15,0) \end{align*}$$

  播放段落

  And the new coordinates of the tip are:
  ::线索的新坐标是:

  $$\begin{align*} (11 + 15, 17) = (26,17) \end{align*}$$

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to calculate the incline (slope) of the hill you came down. 
  ::早些时候,有人要求你计算你所下山的斜坡。

  播放段落

  Since the slope is defined as the change in "y" divided by the change in "x", we can find the slope of the vector representing your trip down the hill:
  ::由于斜坡的定义是“y”的变动除以“x”的变动,我们可以找到矢量的斜坡,表示您在山上旅行:

  播放段落

  $$\begin{align*} \frac{\Delta y}{\Delta x} = \frac{-256 - 0}{12 - 0} = \frac{-256}{12} \approx -21.33 \end{align*}$$
  ::{\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}... {\fn黑体\fs22\bord1\shad0\3aHBE\4aH00\fscx67\fscy66\2cHFFFFFF\3cH808080}...

  播放段落

  This means that for every foot the hill changed in the "x" direction, it went down 21.33 feet in the "y" direction. That's a steep hill indeed!
  ::也就是说,对于每一英尺的山体, 山体在“x”方向上的变化, 山体在“y”方向下方21.33英尺。这的确是一个陡峭的山体!

  播放段落

  Example 2
  ::例2

  播放段落

  Find the magnitude of the horizontal and vertical components of the following vector given the following coordinates of their initial and terminal points.
  ::根据下列初始点和终点点的坐标,查找下列矢量的横向和垂直组成部分的大小。

  播放段落

  $\begin{align*}\text{initial} = (-3,8) \qquad \qquad \quad \text{terminal} = (2, -1)\end{align*}$
  ::初始=( - 3,8) 终点=( 2, - 1)

  播放段落

  The vector needs to be translated to (0,0). Also, recall that magnitudes are always positive.
  ::矢量需要转换为(0,0),还要提醒注意,数值总是正值。

  $\begin{align*}(-3, 8) + (3, -8) = (0, 0) \qquad \qquad (2, -1) + (3, -8) = (5, -9)\end{align*}$

  播放段落

  horizontal $\begin{align*}= 5\end{align*}$ , vertical $\begin{align*}= 9\end{align*}$
  ::水平=5,垂直=9

  播放段落

  Example 3
  ::例3

  播放段落

  Find the magnitude of the horizontal and vertical components of the following vector given the following coordinates of their initial and terminal points.
  ::根据下列初始点和终点点的坐标,查找下列矢量的横向和垂直组成部分的大小。

  播放段落

  $\begin{align*}\text{initial} = (7, 13) \qquad \qquad \quad \ \text{terminal} = (11, 19)\end{align*}$
  ::初始=( 7, 13) 终端=( 11, 19)

  播放段落

  The vector needs to be translated to (0,0). Also, recall that magnitudes are always positive.
  ::矢量需要转换为(0,0),还要提醒注意,数值总是正值。

  $\begin{align*}(7, 13) + (-7, -13) = (0, 0)\qquad \qquad (11, 19) + (-7, -13) = (4, 6)\end{align*}$

  播放段落

  horizontal $\begin{align*}= 4\end{align*}$ , vertical $\begin{align*}= 6\end{align*}$
  ::水平=4, 垂直=6

  播放段落

  Example 4
  ::例4

  播放段落

  Find the magnitude of the horizontal and vertical components of the following vector given the following coordinates of their initial and terminal points.
  ::根据下列初始点和终点点的坐标,查找下列矢量的横向和垂直组成部分的大小。

  播放段落

  $\begin{align*}\text{initial} = (4.2, -6.8) \qquad \quad \ \text{terminal} = (-1.3, -9.4)\end{align*}$
  :4.2,-6.8)终端=(-1.3,-9.4)

  播放段落

  The vector needs to be translated to (0,0). Also, recall that magnitudes are always positive.
  ::矢量需要转换为(0,0),还要提醒注意,数值总是正值。

  $\begin{align*}(4.2, -6.8) + (-4.2, 6.8) = (0, 0) \qquad \qquad (-1.3, -9.4) + (-4.2, 6.8) = (-5.5, -2.6)\end{align*}$

  播放段落

  horizontal $\begin{align*}= 5.5\end{align*}$ , vertical $\begin{align*}= 2.6\end{align*}$
  ::水平=5.5, 垂直=2.6

  播放段落

  Review
  ::回顾

  播放段落

  In each question below, the initial and terminal coordinates for a vector are given. If the vector is translated so that it is in standard position (with the initial point at the origin), what are the new terminal coordinates?
  ::在下面的每个问题中,给出矢量的初始坐标和终端坐标。如果矢量被翻译为处于标准位置(初始点在源头),新的终端坐标是什么?

  播放段落
  1. initial (2, 5) and terminal (7, -1)
     :2,5)和终点站(7,-1)
  播放段落
  2. initial (4, 3) and terminal (3, -5)
     ::初始(4,3)和终端(3,5)
  播放段落
  3. initial (8, 1) and terminal (-4, 7)
     ::初始(8,1)和终端(4,7)
  播放段落
  4. initial (-2, 7) and terminal (3, 5)
     ::初始(-2,7)和终端(3,5)
  播放段落
  5. initial (4, -3) and terminal (4, 3)
     ::初始(4,3)和终端(4,3)
  播放段落
  6. initial (0, 2) and terminal (6, -4)
     ::初始(0,2)和终端(6,4)

  播放段落

  Find the slope of each vector below with the given terminal coordinates. Assume the vector is in standard position.
  ::以给定的终端坐标查找下方每个矢量的斜度。 假设矢量处于标准位置 。

  播放段落
  7. terminal (6, 7)
     ::终端终端(6,7)
  播放段落
  8. terminal (3, 6)
     :3,6)终端(3,6)
  播放段落
  9. terminal (-2, 4)
     :终端站-2,4)
  播放段落
  10. terminal (5, 8)
      :5,8)终端(5,8)
  播放段落
  11. terminal (1, 3)
      ::终端(1,3)

  播放段落

  Find the magnitude of the horizontal and vertical components of each vector given the coordinates of their initial and terminal points.
  ::根据每个矢量初始点和终点点的坐标,查找每个矢量的水平和垂直组成部分的大小。

  播放段落
  12. initial (1, 5) and terminal (1, -3)
      ::和终端(1, 5)和终端(1, 3)
  播放段落
  13. initial (4, 5) and terminal (6, -5)
      ::初始(4,5)和终端(6,5)
  播放段落
  14. initial (6, 1) and terminal (-4, 4)
      ::初始(6,1)和终端(4,4)
  播放段落
  15. initial (-2, 3) and terminal (2, 5)
      ::初始(-2,3)和终端(2,5)

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。