Course: 3.9 确定解决线性系统的最佳办法

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 确定解决线性系统的最佳方法

Collapse Expand
确定解决线性系统的最佳方法
A rental car company, Affordable Autos, charges $30 per day plus $0.51 per mile driven. A second car rental company, Cheap Cars, charges $25 per day plus $0.57 per mile driven. For a short distance , Cheap Cars offers the better deal. At what point (after how many miles in a single day) does the Affordable Autos rental company offer the better deal?
::第二家汽车租赁公司,廉价汽车,每天25美元,每英里0.57美元。短期而言,廉价汽车提供了更好的交易。廉价汽车租赁公司在什么时候(在一天里多英里之后 ) 提供了更好的交易?

Best Method to Solve a Linear System
::解决线性系统的最佳方法

Any of the methods (graphing, substitution, linear combination) learned in this unit can be used to solve a linear system of equations . Sometimes, however it is more efficient to use one method over another based on how the equations are presented. For example,
::在这个单位中学到的任何方法(绘图、替代、线性组合)都可以用于解决直线方程系统。但有时,根据方程的表述方式,使用一种方法比另一种方法更有效。例如,

If both equations are presented in intercept form $\begin{align*}(y=mx+b)\end{align*}$ , then either graphing or substitution would be most efficient.
::如果两个方程式都以截取形式(y=mx+b)显示,那么,图形化或替代最为有效。

If one equation is given in slope intercept form or solved for $\begin{align*}x\end{align*}$ , then substitution might be easiest.
::如果一个方程式以斜坡拦截形式给出或为 x 解答,那么替代可能是最容易的。

If both equations are given in standard form $\begin{align*}(Ax+By=C)\end{align*}$ , then linear combinations is usually most efficient.
::如果两个方程式都以标准格式(Ax+By=C)给出,则线性组合通常效率最高。

Solve the following system.
::解决以下系统。

$\begin{aligned} y & = - x + 5 \\ y & = \frac{1}{2} x + 2 \end{aligned}$
$\begin{align*}y &= -x+5\\ y &= \frac{1}{2}x+2\end{align*}$
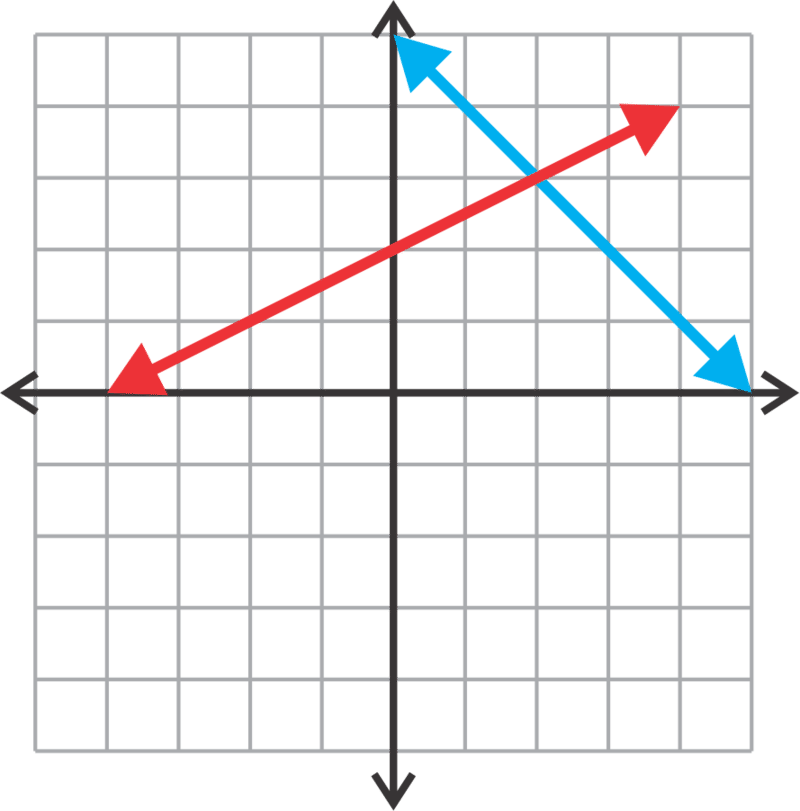
::yux+5y=12x+2

Since both equations are in slope intercept form we could easily graph these lines. The question is whether or not the intersection of the two lines will lie on the “grid” (whole numbers). If not, it is very difficult to determine an answer from a graph. One way to get around this difficulty is to use technology to graph the lines and find their intersection.
::由于两个方程式都以斜坡截截形式出现, 我们可以很容易地绘制这些线条。问题在于两条线的交叉点是否在“ 电网” (完整数字) 上。如果不是, 很难从图表中确定答案。绕过这一困难的一个办法是使用技术来绘制线条的图形并找到它们的交叉点。

The first equation has a $\begin{align*}y-\end{align*}$ intercept of 5 and slope of -1. It is shown here graphed in $\begin{align*}{\color{blue}\mathbf{blue}}\end{align*}$ .
::第一个方程式的Y- interview为 5 , 斜度为 - 1 。此处以蓝色图表显示。

The second equation has a $\begin{align*}y-\end{align*}$ intercept of 2 and a slope of $\begin{align*}\frac{1}{2}\end{align*}$ . It is shown here graphed in $\begin{align*}{\color{red}\mathbf{red}}\end{align*}$ .
::第二个方程式的 Y - intercut 值为 2 , 斜度为 12 。此处以红色图表显示。

The two lines clearly intersect at (2, 3).
::两条线在(2、3)明显交叉。

Alternate Method : Substitution may be the preferred method for students who would rather solve equations algebraically. Since both of these equations are equal to $\begin{align*}y\end{align*}$ , we can let the right hand sides be equal to each other and solve for $\begin{align*}x\end{align*}$ :
::替代方法:替代可能是学生比较喜欢的方法,他们比较喜欢用代数法解析方程式。由于这两个方程式都等于y,我们可以让右手两侧对等并解决x:

$\begin{aligned} - x + 5 = \frac{1}{2} x + 2 \\ 2 (- x + 5 = \frac{1}{2} x + 2) \leftarrow Multiplying the equation by 2 eliminates the fraction . \\ - 2 x + 10 = x + 4 \\ 6 = 3 x \\ x = 2 \end{aligned}$
$\begin{align*}& \quad -x+5 = \frac{1}{2}x+2\\ & \ 2\left(-x+5=\frac{1}{2}x+2\right) \ \leftarrow \text{Multiplying the equation by 2 eliminates the fraction}.\\ & -2x+10=x+4\\ & \qquad \quad \ \ 6=3x\\ & \qquad \quad \ \ x=2\end{align*}$
::=x+5=12x+2 2(-x+5=12x+2) 将方程除去分数。- 2x+10=x+4 6=3xx=2

Now solve for $\begin{align*}y\end{align*}$ :
::现在为 y 解决 :

$\begin{aligned} y & = - (2) + 5 \\ y & = 3 \end{aligned}$
$\begin{align*}y &= -(2)+5\\ y &=3\end{align*}$
::y(2)+5y=3

Solution: (2, 3)
::解决办法2,3)

Check your answer:
::检查您的答案 :

$\begin{aligned} 3 & = - 2 + 5 \\ 3 & = \frac{1}{2} 2 + 2 \to 1 + 2 \end{aligned}$
$\begin{align*}3 &= -2+5\\ 3 &= \frac{1}{2}2+2 \rightarrow 1 + 2\end{align*}$

Solve the following system.
::解决以下系统。

$\begin{aligned} 15 x + y & = 24 \\ y & = - 4 x + 2 \end{aligned}$
$\begin{align*}15x+y &=24\\ y &= -4x+2\end{align*}$
::15x+y=24y4x+2

This time one of our equations is already solved for $\begin{align*}y\end{align*}$ . It is easiest here to use this expression to substitute into the other equation and solve:
::这一次我们的一个方程式已经为y解决了。这里最容易使用这个表达式来替代另一个方程式并解决 :

$\begin{aligned} 15 x + (- 4 x + 2) & = 24 \\ 15 x - 4 x + 2 & = 24 \\ 11 x & = 22 \\ x & = 2 \end{aligned}$
$\begin{align*}15x+(-4x+2) &=24\\ 15x-4x+2 &=24\\ 11x &= 22\\ x &= 2\end{align*}$
::15x+(-4x+2)=2415x-4x+2=2411x=22x=2

Now solve for $\begin{align*}y\end{align*}$ :
::现在为 y 解决 :

$\begin{aligned} y & = - 4 (2) + 2 \\ y & = - 8 + 2 \\ y & = - 6 \end{aligned}$
$\begin{align*}y &= -4(2)+2\\ y &= -8+2\\ y &= -6\end{align*}$
::y4(2)+2y8+2y6

Solution: (2, -6)
::解决办法2,-6)

Check your answer:
::检查您的答案 :

$\begin{aligned} 15 (2) + (- 6) & = 30 - 6 = 24 \\ - 6 = - 4 (2) + 2 & = - 8 + 2 = - 6 \end{aligned}$
$\begin{align*}15(2)+(-6) &= 30-6=24\\ -6 =-4(2)+2 & =-8+2=-6 \end{align*}$

Solve the following system.
::解决以下系统。

$\begin{aligned} - 6 x + 11 y & = 86 \\ 9 x - 13 y & = - 115 \end{aligned}$
$\begin{align*}-6x+11y &= 86\\ 9x-13y &= -115\end{align*}$
::- 6x+11y=869x-13y=115

Both equations in this problem are in standard form so the easiest method to use here is linear combinations. Since the LCM of 6 and 9 is 18, we will multiply the first equation by 3 and the second equation by 2 to eliminate $\begin{align*}x\end{align*}$ first:
::这个问题的两个方程式都以标准形式存在,因此这里最容易使用的方法就是线性组合。由于6和9的 LCM是18,我们将将第一个方程式乘以3,第二个方程式乘以2,以消除x1:

$\begin{aligned} 3 (- 6 x + 11 y = 86) \Rightarrow - 18 x + 33 y = 258 \\ 2 (9 x - 13 y = - 115) \underline{18 x - 26 y = - 230} \\ 7 y = 28 \\ y = 4 \end{aligned}$
$\begin{align*}& 3(-6x+11y=86) \quad \Rightarrow \quad - \cancel{18x}+33y=258\\ & \ \ 2(9x-13y=-115) \qquad \quad \ \underline{\cancel{18x}-26y=-230 \; \; \;}\\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \ 7y=28\\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad y=4\end{align*}$
::3(6x+11y=86)18x+33y=258 2(9x-13y115) 18x-26y230_7y=28y=4

Now solve for $\begin{align*}x\end{align*}$ :
::现在解析 x:

$\begin{aligned} - 6 x + 11 (4) & = 86 \\ - 6 x + 44 & = 86 \\ - 6 x & = 42 \\ x & = - 7 \end{aligned}$
$\begin{align*}-6x+11(4)&=86\\ -6x+44 &=86\\ -6x &=42\\ x &= -7 \end{align*}$
::-6x+11(4)=86-6x+44=86-6x=42x=7

Solution: (-7, 4)
::解决办法-7,4)

Check your answer:
::检查您的答案 :

$\begin{aligned} - 6 (- 7) + 11 (4) & = 42 + 44 = 86 \\ 9 (- 7) - 13 (4) & = - 63 - 52 = - 115 \end{aligned}$
$\begin{align*}-6(-7)+11(4) &= 42+44=86\\ 9(-7)-13(4) &= -63-52=-115 \end{align*}$

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the point at which the Affordable Autos rental company offers the better deal.
::早些时候,有人要求你找到买得起的汽车租赁公司提供更好的交易的点。

Set up equations to represent the total cost (for one day’s rental) for each company:
::设置方程式以代表每家公司的总费用(一天租金):

Affordable Autos $\begin{align*}\Rightarrow y=0.51x+30\end{align*}$
::负担得起的自动 y=0.51x+30

Cheap cars $\begin{align*}\Rightarrow y=0.57x+25\end{align*}$
::廉价汽车 *y=0.57x+25

It is easiest to use substitution here. Substituting $\begin{align*}y=0.51x+30\end{align*}$ into the second equation, we get:
::这里最容易使用替代。将 y= 0. 51x+30 替换为第二个方程, 我们得到 :

$\begin{aligned} 0.51 x + 30 = 0.57 x + 25 \\ 5 = 0.06 x \\ x = 83.333 \end{aligned}$
$\begin{align*}0.51x+30 = 0.57x+25\\ 5 = 0.06x\\ x = 83.333\end{align*}$
::0.51x+30=0.57x+255=0.06xx=83.33

Therefore , Affordable Autos has a better deal if we want to drive more than 83 and one-third miles during our one-day rental.
::因此,如果我们想在我们一天的租用期间驾驶83英里和三分之一英里以上,那么,负担得起的汽车公司就有更好的交易。

Example 2
::例2

Solve the following system using the most efficient method.
::使用最有效的方法解决以下系统。

$\begin{aligned} y & = - 3 x + 2 \\ y & = 2 x - 3 \end{aligned}$
$\begin{align*}y &= -3x+2\\ y &= 2x-3\end{align*}$
::y*% 3x+2y=2x- 3

This one could be solved by graphing, graphing with technology or substitution. This time we will use substitution. Since both equations are solved for $\begin{align*}y\end{align*}$ , we can set them equal and solve for $\begin{align*}x\end{align*}$ :
::这个问题可以通过图形化、技术或替代图解来解决。这次我们将使用替代。由于y 的两个方程式都解决了, 我们可以设定它们等同, x 的解析 :

$\begin{aligned} - 3 x + 2 & = 2 x - 3 \\ 5 & = 5 x \\ x & = 1 \end{aligned}$
$\begin{align*}-3x+2 &= 2x-3\\ 5 &= 5x\\ x &= 1\end{align*}$
::3x+2=2x-35=5xx=1

Now solve for $\begin{align*}y\end{align*}$ :
::现在为 y 解决 :

$\begin{aligned} y & = - 3 (1) + 2 \\ y & = - 3 + 2 \\ y & = - 1 \end{aligned}$
$\begin{align*}y &= -3(1)+2\\ y &= -3+2\\ y &=-1 \end{align*}$
::y3(1)+2y3+2y1

Solution: (1, -1)
::解决办法1,-1)

Example 3
::例3

Solve the following system using the most efficient method.
::使用最有效的方法解决以下系统。

$\begin{aligned} 4 x + 5 y & = - 5 \\ x & = 2 y - 11 \end{aligned}$
$\begin{align*}4x + 5y &= -5\\ x &= 2y-11\end{align*}$
::4x+5y=5x=2y-11

Since the second equation here is solved for $\begin{align*}x\end{align*}$ , it makes sense to use substitution:
::既然这里的第二个方程式为 x 解决了, 使用替代是有道理的 :

$\begin{aligned} 4 (2 y - 11) + 5 y & = - 5 \\ 8 y - 44 + 5 y & = - 5 \\ 13 y & = 39 \\ y & = 3 \end{aligned}$
$\begin{align*}4(2y-11)+5y &= -5\\ 8y-44+5y &= -5\\ 13y &= 39\\ y &= 3\end{align*}$
::4(2y-11)+5y58y-44+5y513y=39y=3

Now solve for $\begin{align*}x\end{align*}$ :
::现在解析 x:

$\begin{aligned} x & = 2 (3) - 11 \\ x & = 6 - 11 \\ x & = - 5 \end{aligned}$
$\begin{align*}x &= 2(3)-11\\ x &= 6-11\\ x &= -5\end{align*}$
::x=2(3)-11x=6-11x=5

Solution: (-5, 3)
::解决办法5,3)

Example 4
::例4

Solve the following system using the most efficient method.
::使用最有效的方法解决以下系统。

$\begin{aligned} 4 x - 5 y & = - 24 \\ - 15 x + 7 y & = - 4 \end{aligned}$
$\begin{align*}4x-5y &= -24\\ -15x+7y &= -4\end{align*}$
::4 - 5y 24 - 15x+7y 4

This time, both equations are in standard form so it makes the most sense to use linear combinations. We can eliminate $\begin{align*}y\end{align*}$ by multiplying the first equation by 7 and the second equation by 5:
::这一次,两个方程式都是标准形式, 所以使用线性组合最有意义。我们可以通过将第一个方程式乘以7 和第二个方程式乘以5 来消除 y :

$\begin{aligned} 7 (4 x - 5 y = - 24) \Rightarrow 28 x - 35 y = - 168 \\ 5 (- 15 x + 7 y = - 4) \underline{- 75 x + 35 y = - 20} \\ - 47 x = - 188 \\ x = 4 \end{aligned}$
$\begin{align*}& \quad \ 7(4x-5y=-24) \quad \Rightarrow \quad 28x-\cancel{35y}=-168\\ & 5(-15x+7y=-4) \qquad \quad \ \underline{-75x+\cancel{35y}=-20 \; \; \;}\\ & \qquad \qquad \qquad \qquad \qquad \qquad \quad \ \ -47x = -188\\ & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \ \ x=4\end{align*}$
::7(4x-5y24)28x-35y1685(-15x+7y4)-75x+35y20_-47x188 x=4)

Now find $\begin{align*}y\end{align*}$ :
::现在找到 y :

$\begin{aligned} 4 (4) - 5 y & = - 24 \\ 16 - 5 y & = - 24 \\ - 5 y & = - 40 \\ y & = 8 \end{aligned}$
$\begin{align*}4(4)-5y &= -24\\ 16-5y &= -24\\ -5y &= -40\\ y &= 8 \end{align*}$
::4 -5y2416 -5y24 -5y40y=8

Solution: (4, 8)
::解决办法: (4,8)

Review
::回顾

Solve the following systems using linear combinations.
::使用线性组合解决以下系统。

.

$\begin{aligned} 5 x - 2 y & = - 1 \\ 8 x + 4 y & = 56 \end{aligned}$
$\begin{align*}5x-2y &= -1\\ 8x+4y &= 56\end{align*}$

.

$\begin{aligned} 3 x + y & = - 16 \\ - 4 x - y & = 21 \end{aligned}$
$\begin{align*}3x+y &= -16\\ -4x-y &= 21\end{align*}$

.

$\begin{aligned} 7 x + 2 y & = 4 \\ y & = - 4 x + 1 \end{aligned}$
$\begin{align*}7x+2y &= 4\\ y &= -4x+1\end{align*}$

.

$\begin{aligned} 6 x + 5 y & = 25 \\ x & = 2 y + 24 \end{aligned}$
$\begin{align*}6x+5y &= 25\\ x &= 2y+24\end{align*}$

.

$\begin{aligned} - 8 x + 10 y & = - 1 \\ 2 x - 6 y & = 2 \end{aligned}$
$\begin{align*}-8x+10y &= -1\\ 2x-6y &= 2\end{align*}$

.

$\begin{aligned} 3 x + y & = 18 \\ - 7 x + 3 y & = - 10 \end{aligned}$
$\begin{align*}3x+y &= 18\\ -7x+3y &= -10\end{align*}$

.

$\begin{aligned} 2 x + 15 y & = - 3 \\ - 3 x - 5 y & = - 6 \end{aligned}$
$\begin{align*}2x+15y &= -3\\ -3x-5y &= -6\end{align*}$

.

$\begin{aligned} 15 x - y & = 19 \\ 13 x + 2 y & = 48 \end{aligned}$
$\begin{align*}15x-y &= 19\\ 13x+2y &= 48\end{align*}$

.

$\begin{aligned} x & = - 9 y - 2 \\ - 2 x - 15 y & = 6 \end{aligned}$
$\begin{align*}x &= -9y-2\\ -2x-15y &= 6\end{align*}$

.

$\begin{aligned} 3 x - 4 y & = 1 \\ - 2 x + 3 y & = 1 \end{aligned}$
$\begin{align*}3x-4y &= 1\\ -2x+3y &= 1\end{align*}$

.

$\begin{aligned} x - y & = 2 \\ 3 x - 2 y & = - 7 \end{aligned}$
$\begin{align*}x-y &= 2\\ 3x-2y &= -7\end{align*}$

.

$\begin{aligned} 3 x + 12 y & = - 18 \\ y & = - \frac{1}{4} x - \frac{3}{2} \end{aligned}$
$\begin{align*}3x+12y &= -18\\ y &= -\frac{1}{4}x-\frac{3}{2}\end{align*}$

.

$\begin{aligned} - 2 x - 8 y & = - 2 \\ x & = \frac{1}{2} y + 10 \end{aligned}$
$\begin{align*}-2x-8y &= -2\\ x &= \frac{1}{2}y+10\end{align*}$

.

$\begin{aligned} 14 x + y & = 3 \\ - 21 x - 3 y & = - 3 \end{aligned}$
$\begin{align*}14x+y &= 3\\ -21x-3y &= -3\end{align*}$

.

$\begin{aligned} y & = \frac{4}{5} x + 7 \\ 8 x - 10 y & = 2 \end{aligned}$
$\begin{align*}y &= \frac{4}{5}x+7\\ 8x-10y &= 2\end{align*}$

Solve the following word problem by creating and solving a system of linear equations.
::通过创建和解决线性方程式系统来解决以下字词问题。

Jack and James each buy some small fish for their new aquariums. Jack buys 10 clownfish and 7 goldfish for $28.25. James buys 5 clownfish and 6 goldfish for $17.25. How much does each type of fish cost?
::杰克和詹姆斯每人买一些小鱼来购买新的水族馆。杰克买10只小丑鱼和7条金鱼,28.25美元。詹姆斯买5只小丑鱼和6条金鱼,17.25美元。每种鱼要多少钱?

The sum of two numbers is 35. The larger number is one less than three times the smaller number. What are the two numbers?
::两个数字的总和是35, 最大的数字是比较小的数字少一到三倍。这两个数字是什么?

Rachel offers to go to the coffee shop to buy cappuccinos and lattes for her coworkers. She buys a total of nine drinks for $35.75. If cappuccinos cost $3.75 each and the lattes cost $4.25 each, how many of each drink did she buy?
::Rachel提议去咖啡店为同事购买卡布奇诺和拿铁。她共购买九杯饮料,价格为35.75美元。如果卡布奇诺每人价格为3.75美元,拿铁每人价格为4.25美元,她每杯要买多少?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

确定解决线性系统的最佳方法

Best Method to Solve a Linear System ::解决线性系统的最佳方法

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Best Method to Solve a Linear System
::解决线性系统的最佳方法

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)