5.21 成象和方向

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 以磁向和方向制成

  Collapse Expand

  以磁向和方向制成

  播放段落

  You are out playing soccer with friends after school one day when you and a friend kick the soccer ball at the same time. However, you kick the ball with 55 N of force with a vector like this:
  ::有一天你和一个朋友同时踢足球,你放学后和朋友一起踢足球。然而,你用这样的矢量用55N力踢球:

  

  播放段落

  and your friend kicks the ball with 70 N of force with a vector like this:
  ::你的朋友用70N的力量踢球 用像这样的矢量:

  

  播放段落

  The angle between the two vectors is $\begin{array}{r}{74}^{\circ }\end{array}$ , and combined the graph of both vectors looks like this:
  ::两个矢量之间的角为 74, 将两个矢量的图形合并为如下 :

  

  播放段落

  Can you represent the net force on the ball? What will the vector be like?
  ::你能代表球上的净力吗?矢量会是什么样子?

  播放段落

  Resultant of a Magnitude and Direction
  ::磁力和方向结果

  播放段落

  If we don’t have two perpendicular vectors, we can still find the magnitude and direction of the resultant without a graphic estimate with a construction using a compass and ruler. This can be accomplished using both the Law of Sines and the Law of Cosines.
  ::如果我们没有两种垂直矢量,我们仍能找到结果的大小和方向,而没有使用指南针和标尺进行构造的图形估计。 这可以用辛斯定律和科辛定律来实现。

  播放段落

  Finding the Magnitude
  ::寻找磁度

  播放段落

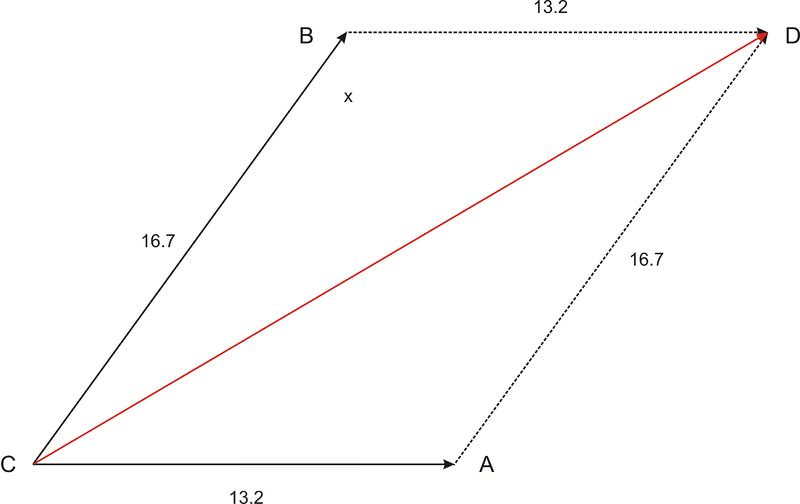
  1.  $\begin{array}{r}\stackrel{\to }{A}\end{array}$ makes a $\begin{array}{r}{54}^{\circ }\end{array}$ angle with $\begin{array}{r}\stackrel{\to }{B}\end{array}$ . The magnitude of $\begin{array}{r}\stackrel{\to }{A}\end{array}$ is 13.2. The magnitude of $\begin{array}{r}\stackrel{\to }{B}\end{array}$ is 16.7. Find the magnitude and direction the resultant makes with the smaller vector.
  ::1. A用 B 生成一个54角度。 A 的大小为 13.2。 B 的大小为 16.7。 用较小的矢量查找产生的大小和方向。

  

  播放段落

  There is no preferred orientation such as a compass direction or any necessary use of $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ coordinates. The problem can be solved without the use of unit vectors.
  ::没有首选方向,如指南针方向或必要使用x和y坐标,问题无需使用单位矢量即可解决。

  播放段落

  In order to solve this problem, we will need to use the parallelogram method. Since vectors only have magnitude and direction, one can move them on the plane to any position one wishes, as long as the magnitude and direction remain the same. First, we will complete the parallelogram: Label the vectors. Move $\begin{array}{r}\stackrel{\to }{b}\end{array}$ so its tail is on the tip of $\begin{array}{r}\stackrel{\to }{a}\end{array}$ . Move $\begin{array}{r}\stackrel{\to }{a}\end{array}$ so its tail is on the tip of $\begin{array}{r}\stackrel{\to }{b}\end{array}$ . This makes a parallelogram because the angles did not change during the translation. Put in labels for the vertices of the parallelogram.
  ::为了解决这个问题, 我们需要使用平行图法。 由于矢量只有大小和方向, 只要大小和方向保持不变, 我们就可以将矢量移动到您想要的任何位置 。 首先, 我们将完成平行图 : 标签矢量和方向 。 移动 b , 其尾部位于 a++++ 的顶端 。 移动 a+++ , 其尾部位于 b++++ 的顶端 。 这样就产生了平行图, 因为在翻译过程中角度没有变化 。 在平行图的顶端贴上标签 。

  

  播放段落

  Since opposite angles in a parallelogram are congruent, we can find $\begin{array}{r}\mathrm{\angle }A\end{array}$ .
  ::由于平行图中的相反角度是相同的,我们可以找到A。

  播放段落

  $$\begin{array}{rl}\mathrm{\angle }CBD+\mathrm{\angle }CAD+\mathrm{\angle }ACB+\mathrm{\angle }BDA& =360\\ 2\mathrm{\angle }CBD+2\mathrm{\angle }ACB& =360\\ \mathrm{\angle }ACB& ={54}^{\circ }\\ 2\mathrm{\angle }CBD& =360-2(54)\\ \mathrm{\angle }CBD& =\frac{360-2(54)}{2}=126\end{array}$$

  
  ::CBD=360(ACB=54)2CBD=360(360)(54)CBD=360(360)(54)CBD=360(360)-2(54)CBD=126(126)。

  播放段落

  Now, we know two sides and the included angle in an oblique triangle. This means we can use the Law of Cosines to find the magnitude of our resultant.
  ::现在,我们知道两面 和包括角度 在一个斜三角形。这意味着我们可以使用 科辛斯定律 来发现我们的结果的大小。

  播放段落

  $$\begin{array}{rl}{x}^2& ={13.2}^2+{16.7}^2-2(13.2)(16.7)\cos 126\\ x^2& =712.272762\\ x& =26.7\end{array}$$

  
  ::x2=13.22+16.72-2(13.2)(16.7)cos=126x2=712.272762x=26.7

  播放段落

  To find the direction, we can use the Law of Sines since we now know an angle and a side across from it. We choose the Law of Sines because it is a proportion and less computationally intense than the Law of Cosines.
  ::为了找到方向,我们可以使用Sines法则,因为我们现在知道一个角度和对面。我们选择Sines法则,因为它比Casines法则的比例和计算强度要低。

  播放段落

  $$\begin{array}{rl}\frac{\sin \theta }{16.7}& =\frac{\sin 126}{26.7}\\ \sin \theta & =\frac{16.7\sin 126}{26.7}\\ \sin \theta & =0.5060143748\\ \theta & ={\sin }^{-1}0.5060={30.4}^{\circ }\end{array}$$

  
  ::126267.7sin 12626.7sin 0.5060143748sin -1 0.506060=30.4

  播放段落

  The magnitude of the resultant is 26.7 and the direction it makes with the smaller vector is $\begin{array}{r}{30.4}^{\circ }\end{array}$ counterclockwise.
  ::其结果的大小为26.7, 其小矢量的方向是30.4- / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / 。

  播放段落

  We can use a similar method to add three or more vectors.
  ::我们可以使用类似的方法来添加三个或三个以上的矢量。

  播放段落

  2. Vector A makes a $\begin{array}{r}{45}^{\circ }\end{array}$ angle with the horizontal and has a magnitude of 3. Vector B makes a $\begin{array}{r}{25}^{\circ }\end{array}$ angle with the horizontal and has a magnitude of 5. Vector $\begin{array}{r}C\end{array}$ makes a $\begin{array}{r}{65}^{\circ }\end{array}$ angle with the horizontal and has a magnitude of 2. Find the magnitude and direction (with the horizontal) of the resultant of all three vectors.
  ::2. 矢量A以水平为45 角度,水平为3. 矢量B以水平为25 角度,水平为5. 矢量C以水平为65 角度,水平为2. 找出所有三种矢量的大小和方向(水平)。

  

  播放段落

  To begin this problem, we will find the resultant using Vector $\begin{array}{r}A\end{array}$ and Vector $\begin{array}{r}B\end{array}$ . We will do this using the parallelogram method like we did above.
  ::首先,我们将使用矢量A和矢量B来发现由此产生的结果。我们将使用上述平行图法这样做。

  

  播放段落

  Since Vector $\begin{array}{r}A\end{array}$ makes a $\begin{array}{r}{45}^{\circ }\end{array}$ angle with the horizontal and Vector $\begin{array}{r}B\end{array}$ makes a $\begin{array}{r}{25}^{\circ }\end{array}$ angle with the horizontal, we know that the angle between the two $\begin{array}{r}(\mathrm{\angle }ADB)\end{array}$ is $\begin{array}{r}{20}^{\circ }\end{array}$ .
  ::由于矢量A以水平为45角, 矢量B以水平为25角, 我们知道两者之间的角是20角。

  播放段落

  To find $\begin{array}{r}\mathrm{\angle }DBE\end{array}$ :
  ::要找到 DBE :

  播放段落

  $$\begin{array}{rl}2\mathrm{\angle }ADB+2\mathrm{\angle }DBE& =360\\ \mathrm{\angle }ADB& ={20}^{\circ }\\ 2\mathrm{\angle }DBE& =360-2(20)\\ \mathrm{\angle }DBE& =\frac{360-2(20)}{2}=160\end{array}$$

  
  ::2 ADB+2DBE=360ADB=202DBE=360-2(20)DBE=360-2(20)2=160

  播放段落

  Now, we will use the Law of Cosines to find the magnitude of $\begin{array}{r}DE\end{array}$ .
  ::现在,我们将使用科辛斯定律 来找到DE的大小。

  播放段落

  $$\begin{array}{rl}D{E}^2& =3^2+5^2-2(3)(5)\cos 160\\ D{E}^2& =62\\ DE& =7.9\end{array}$$

  
  ::DE2=32+52-2(3)(5)(5)cos=160DE2=62DE=7.9

  播放段落

  Next, we will use the Law of Sines to find the measure of $\begin{array}{r}\mathrm{\angle }EDB\end{array}$ .
  ::接下来,我们将使用辛那斯定律 来找到ZZEDB的量度。

  播放段落

  $$\begin{array}{rl}\frac{\sin 160}{7.9}& =\frac{\sin \mathrm{\angle }EDB}{3}\\ \sin \mathrm{\angle }EDB& =\frac{3\sin 160}{7.9}\\ \sin \mathrm{\angle }EDB& =.1299\\ \mathrm{\angle }EDB& ={\sin }^{-1}0.1299={7.46}^{\circ }\end{array}$$

  
  ::EDB=3sin 1607.9sin@EDB=1299_EDB=sin-10.1299=7.46

  播放段落

  We know that Vector $\begin{array}{r}B\end{array}$ forms a $\begin{array}{r}{25}^{\circ }\end{array}$ angle with the horizontal so we add that value to the measure of $\begin{array}{r}\mathrm{\angle }EDB\end{array}$ to find the angle $\begin{array}{r}DE\end{array}$ makes with the horizontal. Therefore, $\begin{array}{r}DE\end{array}$ makes a $\begin{array}{r}{32.46}^{\circ }\end{array}$ angle with the horizontal.
  ::我们知道,矢量B形成一个水平的25角度,因此我们给 EDB 的度量增加这个值, 以找到水平的 DE 角度。 因此, DE 产生一个水平的 32.46角度 。

  播放段落

  Next, we will take $\begin{array}{r}DE\end{array}$ , and we will find the resultant vector of $\begin{array}{r}DE\end{array}$ and Vector $\begin{array}{r}C\end{array}$ from above. We will repeat the same process we used above.
  ::接下来,我们将采取DE,我们将从上面找到DE和矢量C的矢量。我们将重复上面所用的同样过程。

  

  播放段落

  Vector $\begin{array}{r}C\end{array}$ makes a $\begin{array}{r}{65}^{\circ }\end{array}$ angle with the horizontal and $\begin{array}{r}DE\end{array}$ makes a $\begin{array}{r}{32}^{\circ }\end{array}$ angle with the horizontal. This means that the angle between the two $\begin{array}{r}(\mathrm{\angle }CDE)\end{array}$ is $\begin{array}{r}{33}^{\circ }\end{array}$ . We will use this information to find the measure of $\begin{array}{r}\mathrm{\angle }DEF\end{array}$ .
  ::矢量 C 以水平为65 角度, DE 以水平为32 角度。 这意味着两者之间的角为 33。 我们将使用此信息来找到 DEF 的量度 。

  播放段落

  $$\begin{array}{rl}2\mathrm{\angle }CDE+2\mathrm{\angle }DEF& =360\\ \mathrm{\angle }CDE& ={33}^{\circ }\\ 2\mathrm{\angle }DEF& =360-2(33)\\ \mathrm{\angle }DEF& =\frac{360-2(33)}{2}=147\end{array}$$

  
  ::2CDE+2DEF=360CDE=332DEF=360-2(33)DEF=360-2(33)DEF=360-2(33)2=147

  播放段落

  Now we will use the Law of Cosines to find the magnitude of $\begin{array}{r}DF\end{array}$ .
  ::现在,我们将使用科辛斯定律 来找到DF的大小。

  播放段落

  $$\begin{array}{rl}D{F}^2& ={7.9}^2+2^2-2(7.9)(2)\cos 147\\ D{F}^2& =92.9\\ DF& =9.6\end{array}$$

  
  ::DF2=7.92+22-2(7.9)(2)cos=147DF2=92.9DF=9.6

  播放段落

  Next, we will use the Law of Sines to find $\begin{array}{r}\mathrm{\angle }FDE\end{array}$ .
  ::接下来,我们用辛那定律 来找到"FIDE"

  播放段落

  $$\begin{array}{rl}\frac{\sin 147}{9.6}& =\frac{\sin \mathrm{\angle }FDE}{2}\\ \sin \mathrm{\angle }FDE& =\frac{2\sin 147}{9.6}\\ \sin \mathrm{\angle }FDE& =.1135\\ \mathrm{\angle }FDE& ={\sin }^{-1}0.1135={6.5}^{\circ }=7^{\circ }\end{array}$$

  
  ::-=============================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================================

  播放段落

  Finally, we will take the measure of $\begin{array}{r}\mathrm{\angle }FDE\end{array}$ and add it to the $\begin{array}{r}{32}^{\circ }\end{array}$ angle that $\begin{array}{r}DE\end{array}$ forms with the horizontal. Therefore, DF forms a $\begin{array}{r}{39}^{\circ }\end{array}$ angle with the horizontal.
  ::最后,我们将用“FIDE”来测量“FDE”,并将其添加到“DE”与“水平”形成的32“角度上。因此,“DF”与“水平”形成“39”角度。

  播放段落

  3. Two forces of 310 lbs and 460 lbs are acting on an object. The angle between the two forces is $\begin{array}{r}{61.3}^{\circ }\end{array}$ . What is the magnitude of the resultant? What angle does the resultant make with the smaller force?
  ::3. 两支310磅和460磅的力在物体上行动,两支力量之间的角是61.3英寸。 由此产生的规模有多大? 由此产生的角与较小的力量是什么?

  

  播放段落

  We do not need unit vectors here as there is no preferred direction like a compass direction or a specific axis. First, to find the magnitude we will need to figure out the other angle in our parallelogram.
  ::我们这里不需要单位矢量, 因为没有首选方向, 如指南针方向或特定轴。 首先, 要找到大小, 我们需要在平行图中找出另一个角度 。

  

  播放段落

  $$\begin{array}{rl}2\mathrm{\angle }ACB+2\mathrm{\angle }CAD& =360\\ \mathrm{\angle }ACB& ={61.3}^{\circ }\\ 2\mathrm{\angle }CAD& =360-2(61.3)\\ \mathrm{\angle }CAD& =\frac{360-2(61.3)}{2}=118.7\end{array}$$

  
  ::2 ACB+2CAD=360ACB=61.32CAD=360-2(61.3)CAD=360-2(61.3)CAD=360-2(61.3)2=118.7

  播放段落

  Now that we know the other angle, we can find the magnitude using the Law of Cosines.
  ::现在我们知道另一个角度了, 利用科辛定律,我们就能找到其规模。

  播放段落

  $$\begin{array}{rl}{x}^2& ={460}^2+{310}^2-2(460)(310)\cos {118.7}^{\circ }\\ x^2& =444659.7415\\ x& =667\end{array}$$

  
  ::x2=4602+3102-2(460)(310)cos118.7x2=444659.7415x=667

  播放段落

  To find the angle the resultant makes with the smaller force, we will use the Law of Sines.
  ::为了找到由此而来以较小力量产生的角度, 我们将使用Sines定律。

  播放段落

  $$\begin{array}{rl}\frac{\sin \theta }{460}& =\frac{\sin 118.7}{666.8}\\ \sin \theta & =\frac{460\sin 118.7}{666.8}\\ \sin \theta & =.6049283888\\ \theta & ={\sin }^{-1}0.6049={37.2}^{\circ }\end{array}$$

  
  ::118.7666.8sin 460sin118.7666.8sin118.7666.8sin6049283888sin -10.60499=37.2

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to represent the net force on the ball. 
  ::早些时候,你被要求 代表球上的净力。

  播放段落

  As you've seen in this section, you can represent the vector resulting from both of your forces as the resultant of vector addition. Since vectors only have magnitude and direction, one can move them on the plane to any position one wishes, as long as the magnitude and direction remain the same. First, we will complete the parallelogram: Label the vectors. Move $\begin{array}{r}\stackrel{\to }{b}\end{array}$ so its tail is on the tip of $\begin{array}{r}\stackrel{\to }{a}\end{array}$ . Move $\begin{array}{r}\stackrel{\to }{a}\end{array}$ so its tail is on the tip of $\begin{array}{r}\stackrel{\to }{b}\end{array}$ . This makes a parallelogram because the angles did not change during the translation. Put in labels for the vertices of the parallelogram.
  ::正如您在本节中看到的那样, 您可以代表由您的两个力量产生的矢量, 作为矢量添加的结果。 由于矢量只有大小和方向, 只要音量和方向保持不变, 您可以将矢量和方向移动到您想要的任何位置 。 首先, 我们将完成平行图 : 向量标签 。 移动 b , 其尾巴位于 a 的顶端 。 移动 a , 其尾巴位于 b 的顶端 。 由于在翻译过程中角度没有变化, 这使得平行图成为平行图 。 在平行图的顶端贴上标签 。

  

  播放段落

  Since opposite angles in a parallelogram are congruent, we can find angle $\begin{array}{r}A\end{array}$ .
  ::由于平行图中的相反角度是相同的,我们可以找到角度A。

  播放段落

  $$\begin{array}{rl}\mathrm{\angle }CBD+\mathrm{\angle }CAD+\mathrm{\angle }ACB+\mathrm{\angle }BDA& =360\\ 2\mathrm{\angle }CBD+2\mathrm{\angle }ACB& =360\\ \mathrm{\angle }ACB& ={72}^{\circ }\\ 2\mathrm{\angle }CBD& =360-2(72)\\ \mathrm{\angle }CBD& =\frac{360-2(72)}{2}=108\end{array}$$

  
  ::CBD=360*ACB=72*2*CBD=360*CBB=360*CBB=72*2}CBD=360 -2(72)CBD=360 -2(72)CBD=360 -2(72)CBD=360 -2(72)2=108

  播放段落

  Now, we know two sides and the included angle in an oblique triangle. This means we can use the Law of Cosines to find the magnitude of our resultant.
  ::现在,我们知道两面 和包括角度 在一个斜三角形。这意味着我们可以使用 科辛斯定律 来发现我们的结果的大小。

  播放段落

  $$\begin{array}{rl}{x}^2& ={70}^2+{55}^2-2(70)(55)\cos 72\\ x^2& =5545.569\\ x& =74.47\end{array}$$

  
  ::x2=702+552-2(70)(55cos=72x2=5545.569x=74.47)

  播放段落

  To find the direction, we can use the Law of Sines since we now know an angle and a side across from it. We choose the Law of Sines because it is a proportion and less computationally intense than the Law of Cosines.
  ::为了找到方向,我们可以使用Sines法则,因为我们现在知道一个角度和对面。我们选择Sines法则,因为它比Casines法则的比例和计算强度要低。

  播放段落

  $$\begin{array}{rl}\frac{\sin \theta }{70}& =\frac{\sin 108}{74.47}\\ \sin \theta & =\frac{70\sin 108}{74.47}\\ \sin \theta & =0.89397\\ \theta & ={\sin }^{-1}0.89397={63.68}^{\circ }\end{array}$$

  
  ::-=YTET -伊甸园字幕组=-伊甸园字幕组=-伊甸园字幕组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=- 翻译组=-

  播放段落

  The combined force of your kick along with your friend's is 74.47 Newtons and the direction it makes with your kick is $\begin{array}{r}{63.68}^{\circ }\end{array}$ counterclockwise.
  ::你和朋友踢球的结合力是74.47牛顿 踢球的方向是63.68 逆时针

  播放段落

  Example 2
  ::例2

  播放段落

  Forces of 140 Newtons and 186 Newtons act on an object. The angle between the forces is $\begin{array}{r}{43}^{\circ }\end{array}$ . Find the magnitude of the resultant and the angle it makes with the larger force.
  ::140 牛顿和 186 牛顿的部队对一个物体采取行动。 部队之间的角是 43 。 找出由此产生的大小以及它与更大的部队产生的角 。

  播放段落

  magnitude $\begin{array}{r}=304,{18.3}^{\circ }\end{array}$ between resultant and larger force
  ::=304,18.3

  播放段落

  Example 3
  ::例3

  播放段落

  An airplane is traveling at a speed of 155 km/h. It's heading is set at $\begin{array}{r}{83}^{\circ }\end{array}$ while there is a 42.0 km/h wind from $\begin{array}{r}{305}^{\circ }\end{array}$ . What is the airplane's actual heading?
  ::飞机以每小时155公里的速度飞行,航向定在83公里,而305公里的风速为42公里/小时。飞机的实际航向是什么?

  播放段落

  Recall that headings and angles in triangles are complementary. So, an $\begin{array}{r}{83}^{\circ }\end{array}$ heading translates to $\begin{array}{r}{7}^{\circ }\end{array}$ from the horizontal. Adding that to $\begin{array}{r}{35}^{\circ }\end{array}$ ( $\begin{array}{r}{270}^{\circ }\end{array}$ from $\begin{array}{r}{305}^{\circ }\end{array}$ ) we get $\begin{array}{r}{42}^{\circ }\end{array}$ for two of the angles in the parallelogram. So, the other angles in the parallelogram measure $\begin{array}{r}{138}^{\circ }\end{array}$ each, $\begin{array}{r}\frac{360-2(42)}{2}\end{array}$ . Using $\begin{array}{r}{138}^{\circ }\end{array}$ in the Law of Cosines, we can find the diagonal or resultant, $\begin{array}{r}{x}^2={42}^2+{155}^2-2(42)(155)\cos 138\end{array}$ , so $\begin{array}{r}x=188.3\end{array}$ . We then need to find the angle between the resultant and the speed using the Law of Sines. $\begin{array}{r}\frac{\sin a}{42}=\frac{\sin 138}{188.3}\end{array}$ , so $\begin{array}{r}a={8.6}^{\circ }\end{array}$ . To find the actual heading, this number needs to be added to $\begin{array}{r}{83}^{\circ }\end{array}$ , getting $\begin{array}{r}{91.6}^{\circ }\end{array}$ .
  ::提醒注意三角形中的标题和角度是互补的。 因此, 一个 83 标题从水平方向转换为 7 。 添加到 35 ( 305 = 270 = 270 = 270 = 305 = 305 = 302 = 288.3) , 平行图图中的两个角度, 我们得到42 。 因此, 平行图中的其他角度 138 每人 360 - 2( 2/ 422) 。 使用 Cosine 定律中 的 138 或结果的 138 , x2= 422+1552-2 2( 42) ( 155cos 138, so x= 188. 3) 。 然后我们需要找到结果和 使用 Sines 定律的速度之间的角 。 sin_ 4 = sin 1381.88. 3, 所以 a= 8.6 。 要找到实际的标题, 这个数字需要加到 83 91.6 。

  播放段落

  Example 4
  ::例4

  播放段落

  If $\begin{array}{r}\stackrel{\to }{AB}\end{array}$ is any vector, what is $\begin{array}{r}\stackrel{\to }{AB}+\stackrel{\to }{BA}\end{array}$ ?
  ::如果AB是任何矢量, 什么是ABBA?

  播放段落

  $\begin{array}{r}BA\end{array}$ is the same vector as $\begin{array}{r}AB\end{array}$ , but because it starts with $\begin{array}{r}B\end{array}$ it is in the opposite direction. Therefore, when you add the two together, you will get (0,0).
  ::BA 和 AB 是同一种矢量, 但因为它以 B 开头, 它向相反的方向发展。 因此, 当您将两者加在一起时, 你会得到 0,0 。

  播放段落

  Review
  ::回顾

  播放段落

  $\begin{array}{r}\stackrel{\to }{a}\end{array}$ makes a $\begin{array}{r}{42}^{\circ }\end{array}$ angle with $\begin{array}{r}\stackrel{\to }{b}\end{array}$ . The magnitude of $\begin{array}{r}\stackrel{\to }{a}\end{array}$ is 15. The magnitude of $\begin{array}{r}\stackrel{\to }{b}\end{array}$ is 22.
  ::a用 b 生成一个42 角度。 a 的大小为 15 。 b 的大小为 22 。

  播放段落
  1. Find the magnitude of the resultant.
     ::查找结果的大小 。
  播放段落
  2. Find the angle of the resultant makes with the smaller vector.
     ::与较小矢量一起查找所产生矢量的角 。

  播放段落

  $\begin{array}{r}\stackrel{\to }{c}\end{array}$ makes a $\begin{array}{r}{80}^{\circ }\end{array}$ angle with $\begin{array}{r}\stackrel{\to }{d}\end{array}$ . The magnitude of $\begin{array}{r}\stackrel{\to }{c}\end{array}$ is 70. The magnitude of $\begin{array}{r}\stackrel{\to }{d}\end{array}$ is 45.
  ::c 以 d 80 角度。 c 的大小为 70 的大小为 45 的大小为 45 的大小。

  播放段落
  3. Find the magnitude of the resultant.
     ::查找结果的大小 。
  播放段落
  4. Find the angle of the resultant makes with the smaller vector.
     ::与较小矢量一起查找所产生矢量的角 。

  播放段落

  $\begin{array}{r}\stackrel{\to }{e}\end{array}$ makes a $\begin{array}{r}{50}^{\circ }\end{array}$ angle with $\begin{array}{r}\stackrel{\to }{f}\end{array}$ . The magnitude of $\begin{array}{r}\stackrel{\to }{e}\end{array}$ is 32. The magnitude of $\begin{array}{r}\stackrel{\to }{f}\end{array}$ is 10.
  ::e 以 f 制成50角度。 e 的大小是 32 。 f 的大小是 10 。

  播放段落
  5. Find the magnitude of the resultant.
     ::查找结果的大小 。
  播放段落
  6. Find the angle of the resultant makes with the smaller vector.
     ::与较小矢量一起查找所产生矢量的角 。

  播放段落

  $\begin{array}{r}\stackrel{\to }{g}\end{array}$ makes a $\begin{array}{r}{100}^{\circ }\end{array}$ angle with $\begin{array}{r}\stackrel{\to }{h}\end{array}$ . The magnitude of $\begin{array}{r}\stackrel{\to }{g}\end{array}$ is 50. The magnitude of $\begin{array}{r}\stackrel{\to }{h}\end{array}$ is 35.
  ::g 以 h 为 100 角度。 g 的大小为 50 。 h 的大小为 35 。

  播放段落
  7. Find the magnitude of the resultant.
     ::查找结果的大小 。
  播放段落
  8. Find the angle of the resultant makes with the smaller vector.
     ::与较小矢量一起查找所产生矢量的角 。
  播放段落
  9. Two forces of 100 lbs and 120 lbs are acting on an object. The angle between the two forces is $\begin{array}{r}{50}^{\circ }\end{array}$ . What is the magnitude of the resultant?
     ::两股100磅和120磅的力量在物体上行动。两股力量之间的角是50英寸。结果的大小是多少?
  播放段落
  10. Using the information from the previous problem, what angle does the resultant make with the larger force?
      ::使用来自前一个问题的信息, 由此产生的大力产生什么角度?
  播放段落
  11. A force of 50 lbs acts on an object at an angle of $\begin{array}{r}{30}^{\circ }\end{array}$ . A second force of 75 lbs acts on the object at an angle of $\begin{array}{r}-{10}^{\circ }\end{array}$ . What is the magnitude of the resultant force?
      ::50磅的力在30磅的角上对物体起作用。 75磅的第二股力在- 10磅的角上对物体起作用。 由此产生的力有多大?
  播放段落
  12. Using the information from the previous problem, what is the direction of the resultant force?
      ::利用上一个问题的信息,由此产生的部队的方向是什么?
  播放段落
  13. A plane is flying on a bearing of $\begin{array}{r}{30}^{\circ }\end{array}$ at a speed of 450 mph. A wind is blowing with the bearing $\begin{array}{r}{200}^{\circ }\end{array}$ at 50 mph. What is the plane's actual speed and direction?
      ::飞机正以 450 mph 的速度在 30 的 轴上飞行。 风正在吹, 轴上 200 的 轴上为 50 mph 。 飞机的实际速度和方向是什么 ?
  播放段落
  14. Vector A makes a $\begin{array}{r}{30}^{\circ }\end{array}$ angle with the horizontal and has a magnitude of 4. Vector B makes a $\begin{array}{r}{55}^{\circ }\end{array}$ angle with the horizontal and has a magnitude of 6. Vector $\begin{array}{r}C\end{array}$ makes a $\begin{array}{r}{75}^{\circ }\end{array}$ angle with the horizontal and has a magnitude of 3. Find the magnitude and direction (with the horizontal) of the resultant of all three vectors.
      ::矢量 A 以水平为30 角度,其范围为 4. 矢量 B 以水平为55 角度,其范围为 6. 矢量 C 以水平为75 角度,其范围为 3. 找出所有三种矢量(与水平为)的结果的大小和方向。
  播放段落
  15. Vector A makes a $\begin{array}{r}{12}^{\circ }\end{array}$ angle with the horizontal and has a magnitude of 5. Vector B makes a $\begin{array}{r}{25}^{\circ }\end{array}$ angle with the horizontal and has a magnitude of 2. Vector $\begin{array}{r}C\end{array}$ makes a $\begin{array}{r}{60}^{\circ }\end{array}$ angle with the horizontal and has a magnitude of 7. Find the magnitude and direction (with the horizontal) of the resultant of all three vectors.
      ::矢量 A 以水平为方向, 角度为 12 角为 12 角为 5. 矢量 B 以 25 角为 水平为 25 角为 2. 级为 矢量 C 以 水平为 60 角为 7 级, 找出所有三种矢量( 水平) 的结果的大小和方向 。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。