课程： 6.1 极地坐标图

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节极地坐标图

折叠展开
极地坐标图
While playing a game of darts with your friend, you decide to see if you can plot the coordinates of where your darts land. The dartboard looks like this
::在与朋友玩飞镖游戏时,你决定看能不能绘制飞镖降落地点的坐标。

While trying to set up a rectangular coordinate system, your friend tells you that it would be easier to plot the positions of your darts using a ‘‘polar coordinate system’’. Can you do this?
::在试图建立矩形坐标系统时,你的朋友告诉你,使用“极坐标系统”来绘制飞镖的位置比较容易。你能做到这一点吗?

Plots of Polar Coordinates
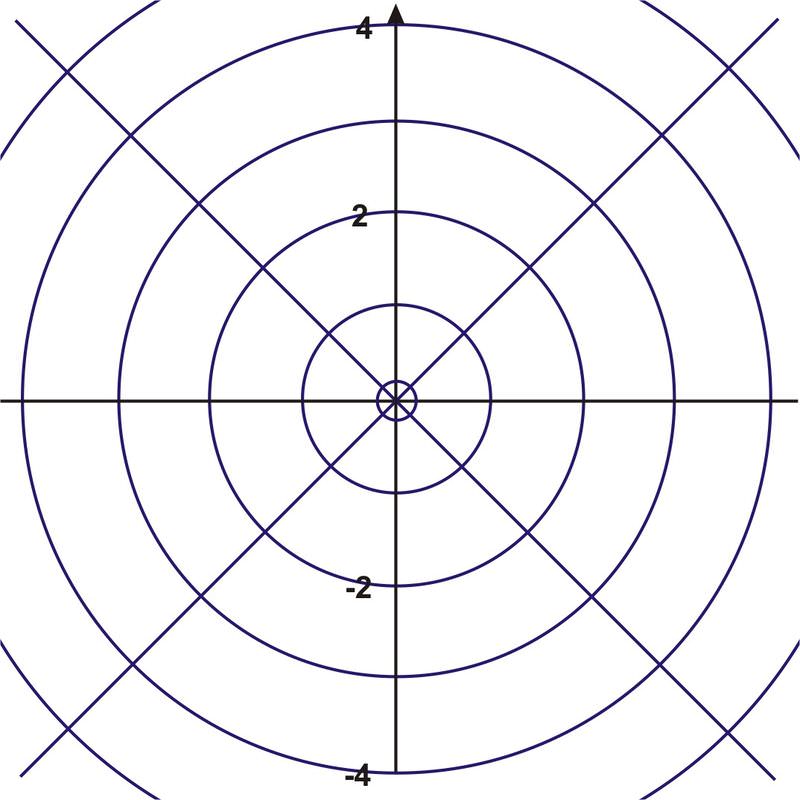
::极地坐标图

The graph paper that you have used for plotting points and sketching graphs has been rectangular grid paper. All points were plotted in a rectangular form $\begin{aligned} (x, y) \end{aligned}$ by referring to a set of perpendicular $\begin{aligned} x - \end{aligned}$ and $\begin{aligned} y - \end{aligned}$ axes. In this section you will discover an alternative to graphing on rectangular grid paper – graphing on circular grid paper.
::您用来绘制点和草图的图表纸是长方形网格纸。所有点都是以长方形(x,y)形式绘制的,指的是一组垂直的x- 和 y- 轴。在本节中,您将找到一个替代矩形网格纸图形的替代方法 — — 在圆形网格纸上绘制图。

Look at the two options below:
::审视以下两个备选方案:

You are all familiar with the rectangular grid paper shown above. However, the circular paper lends itself to new discoveries. The paper consists of a series of concentric circles-circles that share a common center. The common center $\begin{aligned} O \end{aligned}$ , is known as the pole or origin and the polar axis is the horizontal line $\begin{aligned} r \end{aligned}$ that is drawn from the pole in a positive direction. The point $\begin{aligned} P \end{aligned}$ that is plotted is described as a directed distance $\begin{aligned} r \end{aligned}$ from the pole and by the angle that $\begin{aligned} \bar{O P} \end{aligned}$ makes with the polar axis. The coordinates of $\begin{aligned} P \end{aligned}$ are $\begin{aligned} (r, θ) \end{aligned}$ .
::你们都熟悉上面显示的矩形网格纸。但是, 圆形纸可以发现新的发现。圆形纸由一系列具有共同中心的同心圆环环形环形组成。普通中心 O 被称为极或起源, 极轴是从极处向正方向画出的水平线 r 。绘制的点P 被描述为与极点的定向距离 r 和 OP 与极点轴的角。 P 的坐标是 (r, ) 。

These coordinates are the result of assuming that the angle is rotated counterclockwise. If the angle were rotated clockwise then the coordinates of $\begin{aligned} P \end{aligned}$ would be $\begin{aligned} (r, - θ) \end{aligned}$ . These values for $\begin{aligned} P \end{aligned}$ are called and are of the form $\begin{aligned} P (r, θ) \end{aligned}$ where $\begin{aligned} r \end{aligned}$ is the absolute value of the distance from the pole to $\begin{aligned} P \end{aligned}$ and $\begin{aligned} θ \end{aligned}$ is the angle formed by the polar axis and the terminal arm $\begin{aligned} \bar{O P} \end{aligned}$ .
::这些坐标是假设角度是逆时针旋转的结果。如果角度是顺时针旋转的, 则P的坐标是(r, \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\-\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Plotting Points
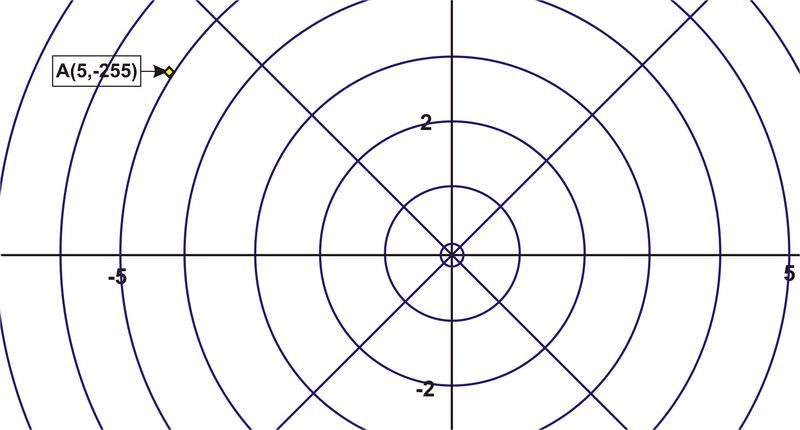
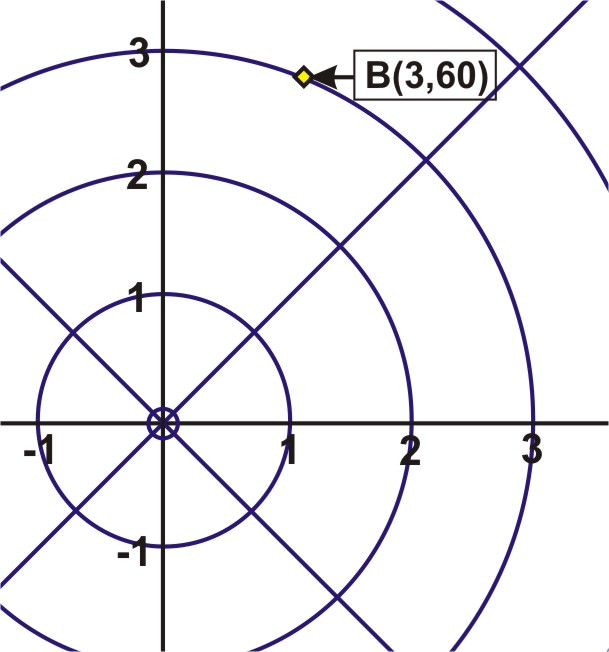
::绘图点

Plot the point $\begin{aligned} A (5, - 255^{\circ}) \end{aligned}$ and the point $\begin{aligned} B (3, 60^{\circ}) \end{aligned}$ .
::绘制点A( 5) 和点B( 3, 60) 。

To plot $\begin{aligned} A \end{aligned}$ , move from the pole to the circle that has $\begin{aligned} r = 5 \end{aligned}$ and then rotate $\begin{aligned} 255^{\circ} \end{aligned}$ clockwise from the polar axis and plot the point on the circle. Label it $\begin{aligned} A \end{aligned}$ .
::绘制 A, 从极点移动到有 r=5 的圆圈, 然后从极轴旋转 255 时钟, 然后绘制圆圈的点。标签 A 。

To plot $\begin{aligned} B \end{aligned}$ , move from the pole to the circle that has $\begin{aligned} r = 3 \end{aligned}$ and then rotate $\begin{aligned} 60^{\circ} \end{aligned}$ counter clockwise from the polar axis and plot the point on the circle. Label it $\begin{aligned} B \end{aligned}$ .
::要绘制 B, 从极点移动到有 r=3 的圆圈, 然后从极轴旋转 60 / counter 时钟, 然后绘制圆圈上的点。标签 B 。

Determining Pairs of Polar Coordinates
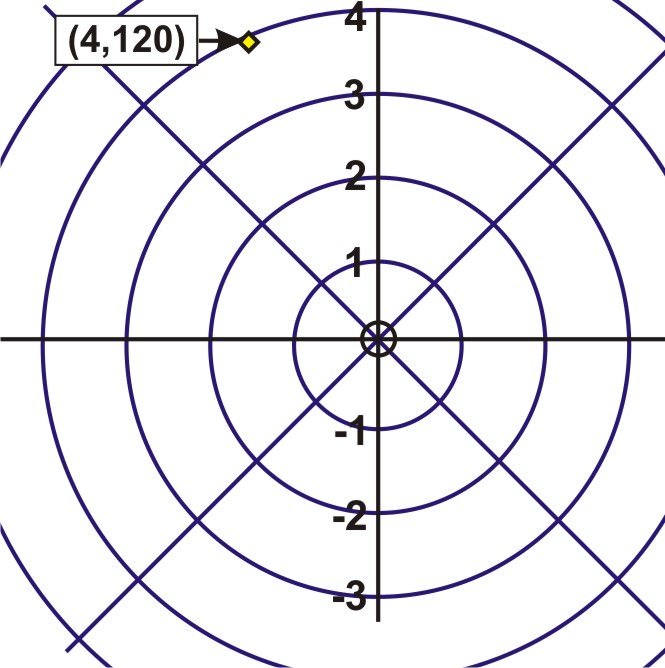
::确定极地坐标对等

Determine four pairs of polar coordinates that represent the following point $\begin{aligned} P (r, θ) \end{aligned}$ such that $\begin{aligned} - 360^{\circ} \leq θ \leq 360^{\circ} \end{aligned}$ .
::确定代表下点P(r,)的四对极坐标,即-360360。

Pair 1 $\begin{aligned} \to (4, 120^{\circ}) . \end{aligned}$ Pair 2 $\begin{aligned} \to (4, - 240^{\circ}) \end{aligned}$ comes from using $\begin{aligned} k = - 1 \end{aligned}$ and $\begin{aligned} (r, θ + 360^{\circ} k), (4, 120^{\circ} + 360 (- 1)) . \end{aligned}$ Pair 3 $\begin{aligned} \to (- 4, 300^{\circ}) \end{aligned}$ comes from using $\begin{aligned} k = 0 \end{aligned}$ and $\begin{aligned} (- r, θ + [2 k + 1] 180^{\circ}), (- 4, 120^{\circ} + [2 (0) + 1] 180^{\circ}) . \end{aligned}$ Pair 4 $\begin{aligned} \to (- 4, - 60^{\circ}) \end{aligned}$ comes from using $\begin{aligned} k = - 1 \end{aligned}$ and $\begin{aligned} (- r, θ + [2 k + 1] 180^{\circ}), (- 4, 120^{\circ} + [2 (- 1) + 1] 180^{\circ}) . \end{aligned}$
::Pair 1 ( 4, 120 ) . Pair 2 ( 4, - 240 ) 源自于使用 k1 和 (r, 360 k) , (4, 120 ) . Pair 3 ( 4, 4, 300 ) , (2k+1, 1,180 ) , (4, 4, 120 [ +1, 180 , (4, 4, 4 - 60 ) , (2k+1,1, ) , (4, 120 ) , [2, 1, +1,180 ] 。

Plotting Polar Coordinates
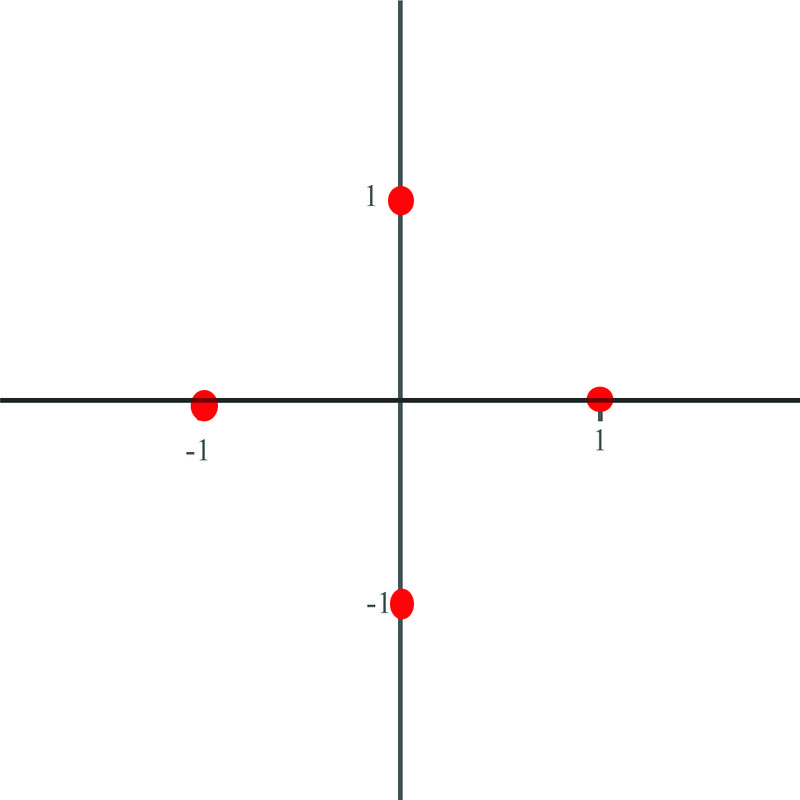
::绘制极地坐标

Plot the following coordinates in polar form and give their description in polar terms: (1,0), (0,1), (-1,0), (-1,1).
::以极地形式绘制以下坐标,并用极地表示1,0,0,0,1,1,1,0,1),(1,1),(1,1)。

The points plotted are shown above. Since each point is 1 unit away from the origin, we know that the radius of each point in polar form will be equal to 1.
::绘制的点显示在上面。由于每个点离原点有1个单位, 我们知道每个点的半径以极形表示等于 1 。

The first point lies on the positive 'x' axis, so the angle in polar coordinates is $\begin{aligned} 0^{\circ} \end{aligned}$ . The second point lies on the positive 'y' axis, so the angle in polar coordinates is $\begin{aligned} 90^{\circ} \end{aligned}$ . The third point lies on the negative 'x' axis, so the angle in polar coordinates is $\begin{aligned} 180^{\circ} \end{aligned}$ . The fourth point lies on the negative 'y' axis, so the angle in polar coordinates is $\begin{aligned} 270^{\circ} \end{aligned}$ .
::第一个点位于正“ x” 轴上, 因此极坐标中的角度是 0 。第二个点位于正“ y” 轴上, 因此极坐标中的角度是 90 。第三点位于负“ x” 轴上, 因此极坐标中的角度是 180 。第四点位于负“ y” 轴上, 因此极坐标中的角度是 270 。

Examples
::实例

Example 1
::例1

Earlier, you were asked to plot the positions of your darts using a polar coordinate system.
::早些时候,你被要求使用极地坐标系统绘制飞镖的位置

Since you have the positions of the darts on the board with both the distance from the origin and the angle they make with the horizontal, you can describe them using polar coordinates.
::由于您在板上的位置与飞镖的起源距离和与水平角的距离相同,您可以用极坐标来描述它们。

As you can see, the positions of the darts are:
::如你所见,飞镖的位置是:

$\begin{aligned} (3, 45^{\circ}) \end{aligned}$ , $\begin{aligned} (6, 90^{\circ}) \end{aligned}$

and
::和

$\begin{aligned} (4, 0^{\circ}) \end{aligned}$

Example 2
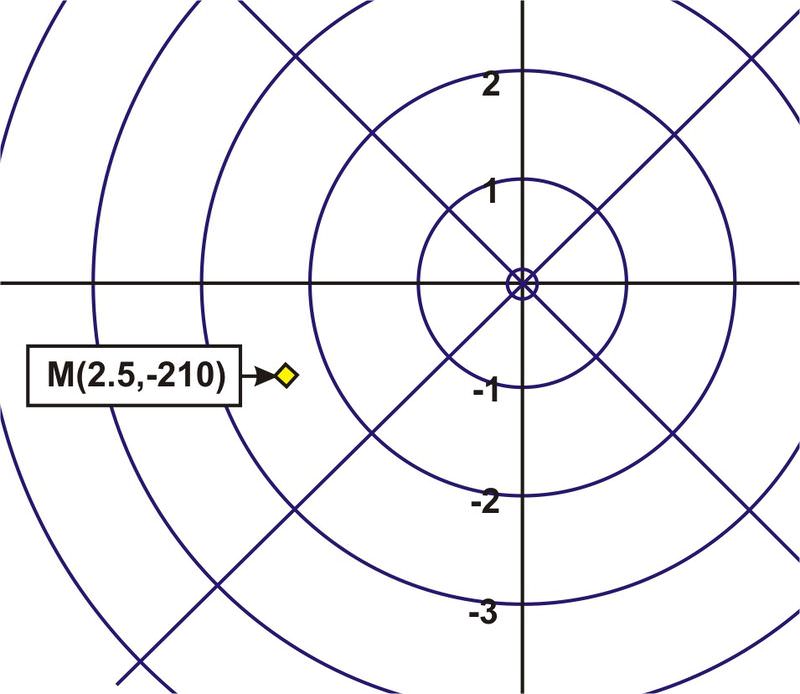
::例2

Plot the point $\begin{aligned} M (2.5, 210^{\circ}) \end{aligned}$ .
::绘制点 M( 2.5, 210 ) 。

Example 3
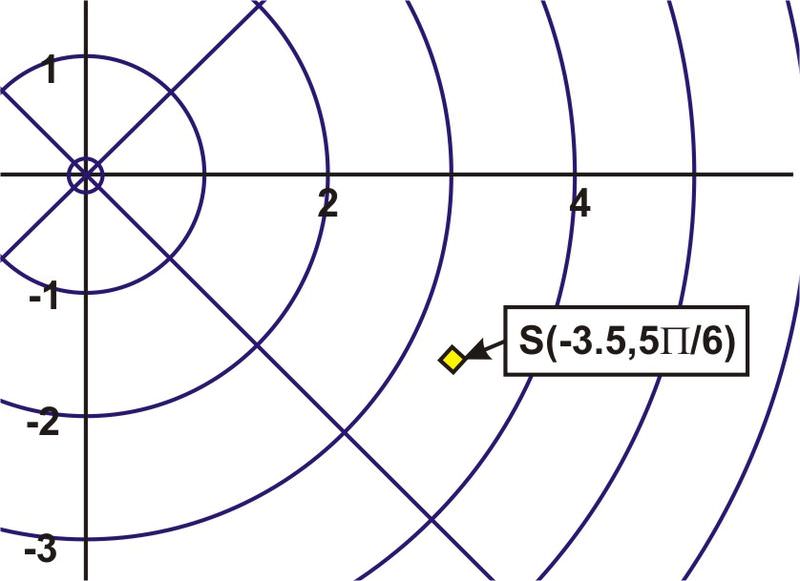
::例3

Plot the point $\begin{aligned} S (- 3.5, \frac{5 π}{6}) \end{aligned}$ .
::绘制点S(-3.5,56)。

Example 4
::例4

Plot the point $\begin{aligned} A (1, \frac{3 π}{4}) \end{aligned}$ .
::绘制点A( 1,3,3,4) 。

Review
::回顾

Plot the following points on a polar coordinate grid.
::在极坐标网格上绘制下列点。

$\begin{aligned} (3, 150^{\circ}) \end{aligned}$

$\begin{aligned} (2, 90^{\circ}) \end{aligned}$

$\begin{aligned} (5, 60^{\circ}) \end{aligned}$

$\begin{aligned} (4, 120^{\circ}) \end{aligned}$

$\begin{aligned} (3, 210^{\circ}) \end{aligned}$

$\begin{aligned} (- 2, 120^{\circ}) \end{aligned}$

$\begin{aligned} (4, - 90^{\circ}) \end{aligned}$

$\begin{aligned} (- 5, - 30^{\circ}) \end{aligned}$

$\begin{aligned} (2, - 150^{\circ}) \end{aligned}$

$\begin{aligned} (- 3, 300^{\circ}) \end{aligned}$

Give three alternate sets of coordinates for the given point within the range $\begin{aligned} - 360^{\circ} \leq θ \leq 360^{\circ} \end{aligned}$ .
::给给给定点在 - 360 360 范围内的三组替代坐标。

$\begin{aligned} (3, 60^{\circ}) \end{aligned}$

$\begin{aligned} (2, 210^{\circ}) \end{aligned}$

$\begin{aligned} (4, 330^{\circ}) \end{aligned}$

Find the length of the arc between the points $\begin{aligned} (2, 30^{\circ}) \end{aligned}$ and $\begin{aligned} (2, 90^{\circ}) \end{aligned}$ .
::查找点(2,30)和点(2,90)之间的弧长度。

Find the area of the sector created by the origin and the points $\begin{aligned} (4, 30^{\circ}) \end{aligned}$ and $\begin{aligned} (4, 90^{\circ}) \end{aligned}$ .
::查找产地和点(4,30)和点(4,90)创造的部门面积。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

极地坐标图

Plots of Polar Coordinates ::极地坐标图

Plotting Points ::绘图点

Determining Pairs of Polar Coordinates ::确定极地坐标对等

Plotting Polar Coordinates ::绘制极地坐标

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Plots of Polar Coordinates
::极地坐标图

Plotting Points
::绘图点

Determining Pairs of Polar Coordinates
::确定极地坐标对等

Plotting Polar Coordinates
::绘制极地坐标

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)