Course: 6.4 极对矩形转换

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 极对矩形转换

Collapse Expand
极对矩形转换
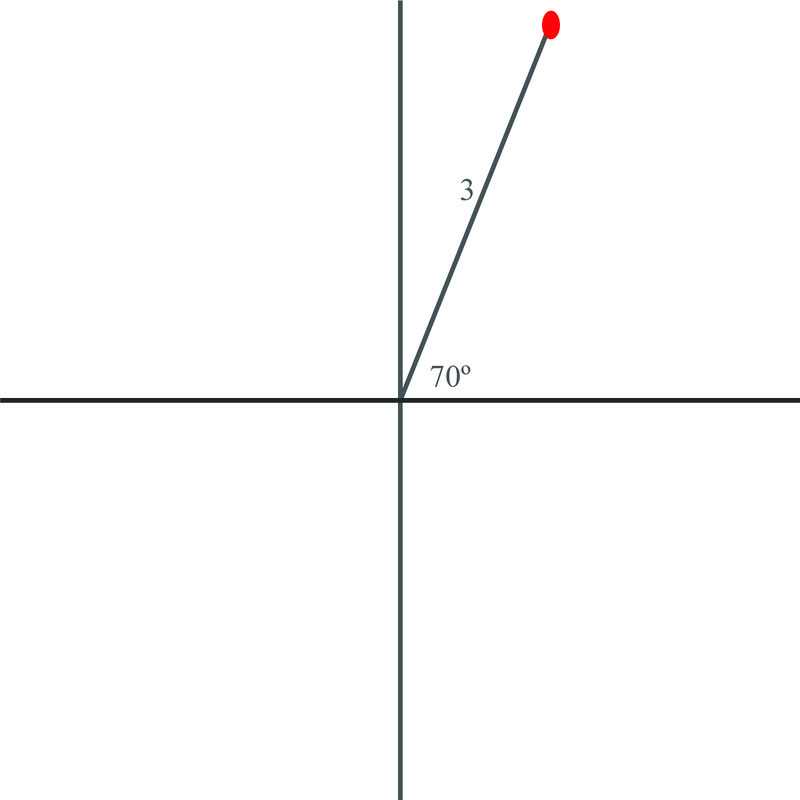
You are hiking one day with friends. When you stop to examine your map, you mark your position on a polar plot with your campsite at the origin, like this
::有一天你和朋友一起徒步远足。当你停下来检查你的地图时, 你用你的营地, 像这样的原地, 标记你在一个极地阴谋上的位置。

You decide to plot your position on a different map, which has a rectangular grid on it instead of a polar plot. Can you convert your coordinates from the polar representation to the rectangular one?
::您决定在不同地图上绘制您的位置, 该地图上有一个矩形网格, 而不是一个极图。您能否将您的坐标从极代表面转换为矩形代表面 ?

Converting Polar Coordinates to Rectangular Coordinates
::将极坐标转换为矩形坐标

Just as $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ are usually used to designate the rectangular coordinates of a point, $\begin{aligned} r \end{aligned}$ and $\begin{aligned} θ \end{aligned}$ are usually used to designate the of the point. $\begin{aligned} r \end{aligned}$ is the distance of the point to the origin. $\begin{aligned} θ \end{aligned}$ is the angle that the line from the origin to the point makes with the positive $\begin{aligned} x - \end{aligned}$ axis.
::正如x和y通常用于指定点的矩形坐标一样,r 和通常用于指定点的矩形坐标。 r 是点与源的距离。是线从源到点与正x- 轴之间的角。

The diagram below shows both polar and Cartesian coordinates applied to a point $\begin{aligned} P \end{aligned}$ . By applying trigonometry, we can obtain equations that will show the relationship between polar coordinates $\begin{aligned} (r, θ) \end{aligned}$ and the rectangular coordinates $\begin{aligned} (x, y) \end{aligned}$
::下图显示适用于P点的极坐标和笛卡尔坐标。通过采用三角测量法,我们可以得到方程,以显示极坐标(r, )和矩形坐标(x,y)之间的关系。

The point $\begin{aligned} P \end{aligned}$ has the polar coordinates $\begin{aligned} (r, θ) \end{aligned}$ and the rectangular coordinates $\begin{aligned} (x, y) \end{aligned}$ .
::P点有极地坐标(r,)和矩形坐标(x,y)。

Therefore
::因此,

$\begin{aligned} x & = r \cos θ & r^{2} = x^{2} + y^{2} \\ y & = r \sin θ & \tan θ = \frac{y}{x} \end{aligned}$

::x=rcosr2=x2+y2y=rsintanyx

These equations, also known as coordinate conversion equations, will enable you to convert from polar to rectangular form .
::这些方程式,也称为坐标转换方程式, 将使您能够从极向矩形转换。

Converting Coordinates
::转换坐标

Given the following polar coordinates, find the corresponding rectangular coordinates of the points: $\begin{aligned} W (4, - 200^{\circ}), H (4, \frac{π}{3}) \end{aligned}$
::根据以下极坐标,找到各点对应的矩形坐标:W(4)-200)、H(4)________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

For $\begin{aligned} W (4, - 200^{\circ}), r = 4 \end{aligned}$ and $\begin{aligned} θ = - 200^{\circ} \end{aligned}$
::W(4,-200),r=4 和200

$\begin{aligned} x & = r \cos θ & y = r \sin θ \\ x & = 4 \cos (- 200^{\circ}) & y = 4 \sin (- 200^{\circ}) \\ x & = 4 (- .9396) & y = 4 (.3420) \\ x & \approx - 3.76 & y \approx 1.37 \end{aligned}$

::x=rcosy=rsinx=4cos(-200)y=4sin(--200)x=4(--.9396y=4(-3420x_3.76y)1.37)

The rectangular coordinates of $\begin{aligned} W \end{aligned}$ are approximately $\begin{aligned} (- 3.76, 1.37) \end{aligned}$ .
::W的矩形坐标约为(-3.76,1.37)。

For $\begin{aligned} H (4, \frac{π}{3}), r = 4 \end{aligned}$ and $\begin{aligned} θ = \frac{π}{3} \end{aligned}$
::H(4,XIII3),r=4和3

$\begin{aligned} x & = r \cos θ & y = r \sin θ \\ x & = 4 \cos \frac{π}{3} & y = 4 \sin \frac{π}{3} \\ x & = 4 (\frac{1}{2}) & y = 4 (\frac{\sqrt{3}}{2}) \\ x & = 2 & y = 2 \sqrt{3} \end{aligned}$

::x=rsinx=4cos3y=4sin3y=4x4(12)y=4(32)x=2y=23

The rectangular coordinates of $\begin{aligned} H \end{aligned}$ are $\begin{aligned} (2, 2 \sqrt{3}) \end{aligned}$ or approximately $\begin{aligned} (2, 3.46) \end{aligned}$ .
::H的矩形坐标为(2,23)或大约(2,3.46)。

Converting Equations
::转换等号

1. In addition to writing polar coordinates in rectangular form, the coordinate conversion equations can also be used to write polar equations in rectangular form.
::1. 除了以矩形形式写出极坐标外,坐标转换方程式还可以用于以矩形形式写出极方程式。

Write the polar equation $\begin{aligned} r = 4 \cos θ \end{aligned}$ in rectangular form.
::以矩形形式写入极方程式 r=4cos。

$\begin{aligned} r & = 4 \cos θ \\ r^{2} & = 4 r \cos θ & M u l t i p l y b o t h s i d e s b y r . \\ x^{2} + y^{2} & = 4 x & r^{2} = x^{2} + y^{2} a n d x = r \cos θ \end{aligned}$

::r= 4cosr2= 4rcos □ 以 r.x2+y2= 4xr2=x2+y2 和 x=rcos= rcos 和 x= rcos= rtip 双侧均匀度为 r.x2+y2= 4xr2=x2+y2= x2+y2

The equation is now in rectangular form. The $\begin{aligned} r^{2} \end{aligned}$ and $\begin{aligned} θ \end{aligned}$ have been replaced. However, the equation, as it appears, does not model any shape with which we are familiar. Therefore, we must continue with the conversion.
::方程现已以矩形形式出现。 r2 和已被替换。但是, 方程似乎并不模拟我们熟悉的任何形状。因此, 我们必须继续转换。

$\begin{aligned} x^{2} - 4 x + y^{2} & = 0 \\ x^{2} - 4 x + 4 + y^{2} & = 4 & C o m p l e t e t h e s q u a r e f o r x^{2} - 4 x . \\ (x - 2)^{2} + y^{2} & = 4 & F a c t o r x^{2} - 4 x + 4. \end{aligned}$

::x2-4x+y2=0x2-4x+4+y2=4 x2-4x.(x-2)2+y2=4Factor x2-4x+4

The rectangular form of the polar equation represents a circle with its centre at (2, 0) and a radius of 2 units.
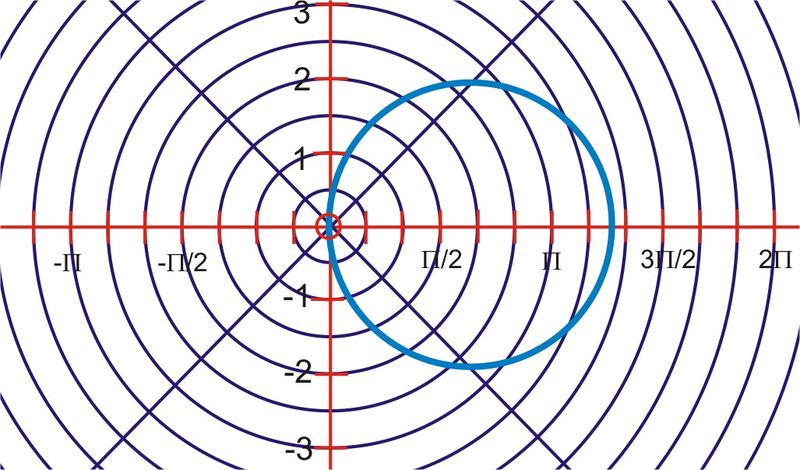
::极方形的矩形表示圆,其中心为(2,0),半径为2个单位。

This is the graph represented by the polar equation $\begin{aligned} r = 4 \cos θ \end{aligned}$ for $\begin{aligned} 0 \leq θ \leq 2 π \end{aligned}$ or the rectangular form $\begin{aligned} (x - 2)^{2} + y^{2} = 4. \end{aligned}$
::这是以 r=4cos或矩形(x-2)2+y2=4的极方方程式 r=4cos 表示的图。

2. Write the polar equation $\begin{aligned} r = 3 \csc θ \end{aligned}$ in rectangular form.
::2. 以矩形形式写出极方程式r=3csc。

$\begin{aligned} r & = 3 \csc θ \\ \frac{r}{\csc θ} & = 3 & d i v i d e b y \csc θ \\ r \cdot \frac{1}{\csc θ} & = 3 \\ r \sin θ & = 3 & \sin θ = \frac{1}{\csc θ} \\ y & = 3 & y = r \sin θ \end{aligned}$

::=3cscrc3divide bycscr1csc3rsin3sin1ccscy=3y=rsin

Examples
::实例

Example 1
::例1

Earlier, you were asked to convert your coordinates from polar representation to the rectangular one.
::早些时候,你被要求将坐标从极表转换为矩形坐标。

You can see from the map that your position is represented in polar coordinates as $\begin{aligned} (3, 70^{\circ}) \end{aligned}$ . Therefore, the radius is equal to 3 and the angle is equal to $\begin{aligned} 70^{\circ} \end{aligned}$ . The rectangular coordinates of this point can be found as follows:
::您可以从地图上看到您的位置以极坐标表示( 3, 70 ) 。因此, 半径等于 3, 角度等于 70 。此点的矩形坐标如下:

$\begin{aligned} x & = r \cos θ & y = r \sin θ \\ x & = 3 \cos (70^{\circ}) & y = 3 \sin (70^{\circ}) \\ x & = 3 (.342) & y = 3 (.94) \\ x & \approx 1.026 & y \approx 2.82 \end{aligned}$

::x=rcosy=rsinx=3cos(70)y=3sin(70)xx=3(3.442)y=3(94×1.026y2.82)

Example 2
::例2

Write the polar equation $\begin{aligned} r = 6 \cos θ \end{aligned}$ in rectangular form.
::以矩形形式写入极方方程式 r= 6cos。

$\begin{aligned} r & = 6 \cos θ \\ r^{2} & = 6 r \cos θ \\ x^{2} + y^{2} & = 6 x \\ x^{2} - 6 x + y^{2} & = 0 \\ x^{2} - 6 x + 9 + y^{2} & = 9 \\ (x - 3)^{2} + y^{2} & = 9 \end{aligned}$

::r=6cosr2=6rcosx2+y2=6xx2-6x+y2=0x2-6x+9+y2=9(x-3)2+y2=9

Example 3
::例3

Write the polar equation $\begin{aligned} r \sin θ = - 3 \end{aligned}$ in rectangular form.
::以矩形形式写入极方方程 rsin3 。

$\begin{aligned} r \sin θ & = - 3 \\ y & = - 3 \end{aligned}$

::

Example 4
::例4

Write the polar equation $\begin{aligned} r = 2 \sin θ \end{aligned}$ in rectangular form.
::以矩形形式写入极方方程式 r=2sin。

$\begin{aligned} r & = 2 \sin θ \\ r^{2} & = 2 r \sin θ \\ x^{2} + y^{2} & = 2 y \\ y^{2} - 2 y & = - x^{2} \\ y^{2} - 2 y + 1 & = - x^{2} + 1 \\ (y - 1)^{2} & = - x^{2} + 1 \\ x^{2} + (y - 1)^{2} & = 1 \end{aligned}$

::r2=2rsinx2+y2=2yy2 -2y2 -2yx2y2-2-2y+1x2+1(y- 1)2x2+1(y- 1)2x2+1x2+1x2+(y- 1)2=1

Review
::回顾

Given the following polar coordinates, find the corresponding rectangular coordinates of the points.
::根据以下极坐标,找到相应的各点的矩形坐标。

$\begin{aligned} (2, \frac{π}{6}) \end{aligned}$

$\begin{aligned} (4, \frac{2 π}{3}) \end{aligned}$

$\begin{aligned} (5, \frac{π}{3}) \end{aligned}$

$\begin{aligned} (3, \frac{π}{4}) \end{aligned}$

$\begin{aligned} (6, \frac{3 π}{4}) \end{aligned}$

Write each polar equation in rectangular form.
::以矩形形式写下每个极方程。

$\begin{aligned} r = 3 \sin θ \end{aligned}$
::r=3sin

$\begin{aligned} r = 2 \cos θ \end{aligned}$
::r=2cos

$\begin{aligned} r = 5 \csc θ \end{aligned}$
::r=5csc

$\begin{aligned} r = 3 \sec θ \end{aligned}$
::r=3sec

$\begin{aligned} r = 6 \cos θ \end{aligned}$
::r=6cos

$\begin{aligned} r = 8 \sin θ \end{aligned}$
::r=8sin____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

$\begin{aligned} r = 2 \csc θ \end{aligned}$
::r=2csc

$\begin{aligned} r = 4 \sec θ \end{aligned}$
::r=4sec

$\begin{aligned} r = 3 \cos θ \end{aligned}$
::r=3cos

$\begin{aligned} r = 5 \sin θ \end{aligned}$
::r=5sin

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

极对矩形转换

Converting Polar Coordinates to Rectangular Coordinates ::将极坐标转换为矩形坐标

Converting Coordinates ::转换坐标

Converting Equations ::转换等号

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Converting Polar Coordinates to Rectangular Coordinates
::将极坐标转换为矩形坐标

Converting Coordinates
::转换坐标

Converting Equations
::转换等号

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)