课程： 6.5 极地矩形转换

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节矩形到极地转换

折叠展开
矩形到极地转换
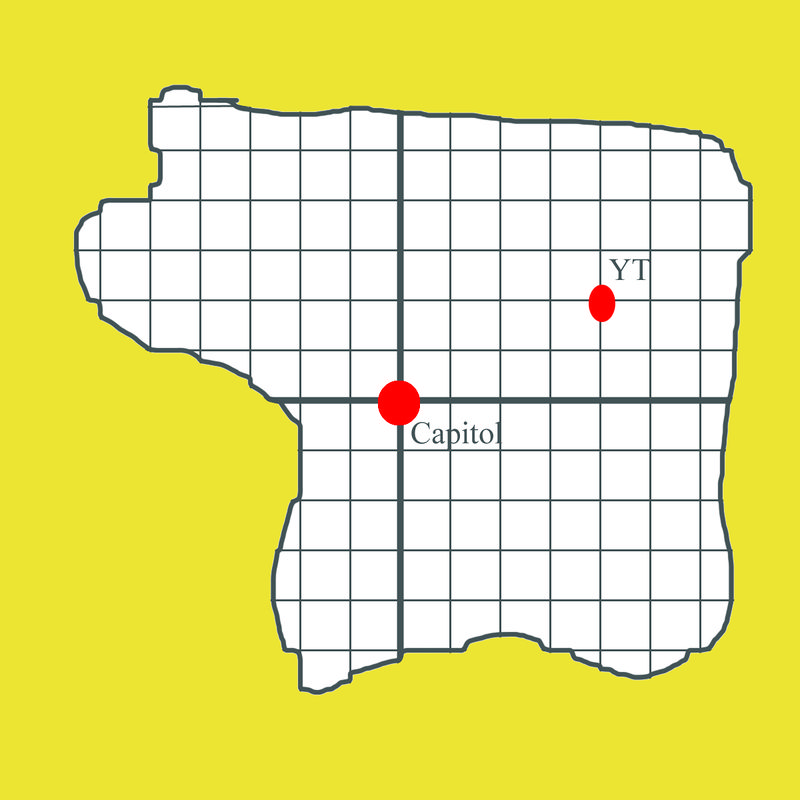
You are looking at a map of your state with a rectangular coordinate grid. It looks like this
::您正在用矩形坐标网格查看您状态的地图。看起来是这样

You realize that if you convert the coordinates of Your town (labelled with a "YT") to , you can more easily see the distance between the Capitol at the origin and Your town. Can you make this conversion from rectangular to polar coordinates?
::您意识到, 如果您将您的城镇坐标( 标签为“ YT ” ) 转换为 , 您可以更容易地看到首都与您的城镇之间的距离。您能够将矩形坐标转换为极地坐标吗 ?

Converting Rectangular Coordinates to Polar Coordinates
::将矩形坐标转换为极坐标

When converting rectangular coordinates to polar coordinates, we must remember that there are many possible polar coordinates. We will agree that when converting from rectangular coordinates to polar coordinates, one set of polar coordinates will be sufficient for each set of rectangular coordinates.
::当将矩形坐标转换为极坐标时,我们必须记住,有许多可能的极坐标。我们会同意,当从矩形坐标转换为极坐标时,每组矩形坐标就有足够的一组极坐标。

Most graphing calculators are programmed to complete the conversions and they too provide one set of coordinates for each conversion. The conversion of rectangular coordinates to polar coordinates is done using the and the Arctangent function. The Arctangent function only calculates angles in the first and fourth quadrants so $\begin{align*}\pi\end{align*}$ radians must be added to the value of $\begin{align*}\theta\end{align*}$ for all points with rectangular coordinates in the second and third quadrants.
::大多数图形化计算器都编程完成转换,它们也为每次转换提供一套坐标。矩形坐标转换为极坐标时,使用弧度函数和弧度函数进行。弧度函数只计算第一和第二四方位角的角,因此,对于第二和第三四方位具有矩形坐标的所有点,弧度必须加到 + 的值。

In addition to these formulas, $\begin{align*}r = \sqrt{x^2 + y^2}\end{align*}$ is also used in converting rectangular coordinates to polar form .
::除这些公式外,r=x2+y2还用于将矩形坐标转换成极形。

Converting Coordinates
::转换坐标

Convert the following rectangular coordinates to polar form.
::将以下矩形坐标转换为极形。

1. $\begin{align*}P (3, -5)\end{align*}$
::1. P(3, - 5)

For $\begin{align*}P (3, -5) \ x = 3\end{align*}$ and $\begin{align*}y = -5\end{align*}$ . The point is located in the fourth quadrant and $\begin{align*}x > 0\end{align*}$ .
::P( 3, - 5) x=3 和 y5. 点位于第四象限和 x>0 。

$\begin{aligned} r & = \sqrt{x^{2} + y^{2}} & θ = \arctan \frac{y}{x} \\ r & = \sqrt{(3)^{2} + (- 5)^{2}} & θ = \tan^{- 1} (- \frac{5}{3}) \\ r & = \sqrt{34} & θ \approx - 1.03 \\ r & \approx 5.83 \end{aligned}$
$\begin{align*}r &= \sqrt{x^2 + y^2} && \theta = \ \arctan \frac{y}{x}\\ r &= \sqrt{(3)^2 + (-5)^2} && \theta = \tan^{-1} \left ( -\frac{5}{3} \right )\\ r &= \sqrt{34} && \theta \approx - 1.03\\ r &\approx 5.83\end{align*}$
::rx2+y2arctanyxr=(3)2+(-5)2}tan-1(-53)=341.03r}5.83

The polar coordinates of $\begin{align*}P (3, -5)\end{align*}$ are $\begin{align*}P (5.83, -1.03)\end{align*}$ .
::P(3)-5的极地坐标是P(5.83,-1.03)。

2. $\begin{align*}Q (-9, -12)\end{align*}$
::2. Q(-9)-12

For $\begin{align*}Q (-9, -12) \ x = -9\end{align*}$ and $\begin{align*}y = -5\end{align*}$ . The point is located in the third quadrant and $\begin{align*}x < 0\end{align*}$ .
::Q(- 9,- 12) x9 和 y5. 点位于第三个象限和 x < 0 。

$\begin{aligned} r & = \sqrt{x^{2} + y^{2}} & θ = \arctan \frac{y}{x} + π \\ r & = \sqrt{(- 9)^{2} + (- 12)^{2}} & θ = \tan^{- 1} (\frac{- 12}{- 9}) + π \\ r & = \sqrt{225} & θ \approx 4.07 \\ r & = 15 \end{aligned}$
$\begin{align*}r & = \sqrt{x^2 + y^2} && \theta = \arctan \frac{y}{x} + \pi \\ r & = \sqrt{(-9)^2 + (-12)^2} && \theta = \tan^{-1} \left (\frac{-12}{-9} \right ) + \pi \\ r & = \sqrt{225} && \theta \approx 4.07 \\ r & = 15\end{align*}$
::r= rx2+y2 arctanyxr= (--)92+(-)12)2tan-1(--12-9)r= 2254.07r=15

The polar coordinates of $\begin{align*}Q (-9, -12)\end{align*}$ are $\begin{align*}Q (15, 4.07) \end{align*}$
::Q(- 9) 的极坐标为Q( 15, 4. 07) 。

3. $\begin{align*}Q (2, 7)\end{align*}$
::3. 问题(2,7)

For $\begin{align*}Q (2, 7) \ x = 2\end{align*}$ and $\begin{align*}y = 7\end{align*}$ . The point is located in the first quadrant and $\begin{align*}x > 0\end{align*}$ .
::对于 Q(2,7) x=2和y=7, 点位于第一个象限和 x>0 。

$\begin{aligned} r & = \sqrt{x^{2} + y^{2}} & θ = \arctan \frac{y}{x} + π \\ r & = \sqrt{(2)^{2} + (7)^{2}} & θ = \tan^{- 1} (\frac{7}{2}) + π \\ r & = \sqrt{54} & θ \approx 74.05 \\ r & \approx 7.35 \end{aligned}$
$\begin{align*}r & = \sqrt{x^2 + y^2} && \theta = \arctan \frac{y}{x} + \pi \\ r & = \sqrt{(2)^2 + (7)^2} && \theta = \tan^{-1} \left (\frac{7}{2} \right ) + \pi \\ r & = \sqrt{54} && \theta \approx 74.05 \\ r &\approx 7.35\end{align*}$
::rx2+y2arctanyxr=(2)2+(7)2tan-1(72r=5474.05r7.35)

The polar coordinates of $\begin{align*}Q (2, 7)\end{align*}$ are $\begin{align*}Q (7.35, 74.05) \end{align*}$
::Q(2,7)的极坐标为Q(7.35,74.05)

Examples
::实例

Example 1
::例1

Earlier, you were asked to convert rectangular coordinates to polar coordinates.
::早些时候,你被要求将矩形坐标转换为极坐标。

To convert these rectangular coordinates into polar coordinates, first use the Pythagorean Theorem:
::要将这些矩形坐标转换为极坐标,首先使用毕达哥伦理论:

$\begin{aligned} r = \sqrt{(4)^{2} + (2)^{2}} = \sqrt{20} \approx 4.47 \end{aligned}$
$\begin{align*}r = \sqrt{(4)^2 + (2)^2} = \sqrt{20} \approx 4.47\end{align*}$
::r=(4)2+(2)2=204.47

and then use the tangent function to find the angle:
::然后使用正切函数查找角度 :

$\begin{aligned} θ = \arctan \frac{4}{2} = {63.43}^{\circ} \end{aligned}$
$\begin{align*}\theta = \arctan \frac{4}{2} = 63.43^\circ\end{align*}$
::arctan42=63.43

The polar coordinates for Yourtown are $\begin{align*}YT(4.47,63.43^\circ)\end{align*}$
::你镇的极地坐标是YT(4.47 63.43)

Example 2
::例2

Write the following rectangular point in polar form: $\begin{align*}A(-2, 5)\end{align*}$ using radians
::以极形写下以下矩形点:A(-2,5),使用弧度

For $\begin{align*}A (-2, 5) x = -2\end{align*}$ and $\begin{align*}y = 5\end{align*}$ . The point is located in the second quadrant and $\begin{align*}x < 0\end{align*}$ .
$\begin{aligned} r = \sqrt{(- 2)^{2} + (5)^{2}} = \sqrt{29} \approx 5.39, θ = \arctan \frac{5}{- 2} + π = 1.95. \end{aligned}$
$\begin{align*}r = \sqrt{(-2)^2 + (5)^2} = \sqrt{29} \approx 5.39, \ \theta = \ \arctan \frac{5}{-2} + \pi = 1.95.\end{align*}$ The polar coordinates for the rectangular coordinates $\begin{align*}A(-2,5)\end{align*}$ are $\begin{align*}A(5.39,1.95)\end{align*}$
::A(-2,5,5x2和y=5.)的点位于第二个象限和 x<0. r=(-2)2+(5)2=295.39, arctan_5-21.95。矩形坐标A(-2,5)的极坐标为A(-539,1.95)。

Example 3
::例3

Write the following rectangular point in polar form: $\begin{align*}B(5, -4)\end{align*}$ using radians
::用极形写下以下的矩形点:B(5)-(4),使用弧度

For $\begin{align*}B (5,-4) x = 5\end{align*}$ and $\begin{align*}y = -4\end{align*}$ . The point is located in the fourth quadrant and $\begin{align*}x > 0\end{align*}$ .
$\begin{aligned} r = \sqrt{(5)^{2} + (- 4)^{2}} = \sqrt{41} \approx 6.4, θ = \tan^{- 1} (\frac{- 4}{5}) \approx - 0.67 \end{aligned}$
$\begin{align*}r = \sqrt{(5)^2 + (-4)^2} = \sqrt{41} \approx 6.4, \ \theta = \tan^{-1} \left (\frac{-4}{5} \right ) \approx -0.67\end{align*}$
::对于 B( 5, 4) x=5 和 y4, 点位于第四象限和 x>0. r= (5)2+( 4) 2= 416. 4, - 1 (- 45) 0. 67。

Example 4
::例4

Write the following rectangular point in polar form: $\begin{align*}C(1, 9)\end{align*}$ using degrees
::以极形写下以下矩形点:C(1,9),使用度

The polar coordinates for the rectangular coordinates $\begin{align*}B(5, -4)\end{align*}$ are $\begin{align*}A(6.40, -0.67)\end{align*}$
::矩形坐标B(5)-4的极坐标为A(6.40)-0.67。

$\begin{align*}C(1, 9)\end{align*}$ is located in the first quadrant.
$\begin{aligned} r = \sqrt{1^{2} + 9^{2}} = \sqrt{82} \approx 9.06, θ = \tan^{- 1} \frac{9}{1} \approx 83.66. \end{aligned}$
$\begin{align*}r = \sqrt{1^2 + 9^2} = \sqrt{82} \approx 9.06, \ \theta = \tan^{-1} \frac{9}{1} \approx 83.66.\end{align*}$
::C(1,9)位于第一个象限内,r=12+92=829.06,tan-19183.66。

Review
::回顾

Write the following points, given in rectangular form, in polar form using radians where $\begin{align*}0\leq \theta \leq 2\pi\end{align*}$ .
::以矩形形式,用弧度02以极形形式写下以下各点。

(1,3)

(2,5)

(-2,3)

(2,-1)

(3,2)

(4,5)

(-1,2)

(-3,3)

(-2,5)

(1,-4)

(5,2)

(1,6)

For each equation, convert the rectangular equation to polar form.
::每个方程,将矩形方程转换为极形。

$\begin{align*}x=5\end{align*}$
::x=5x=5

$\begin{align*}2x-3y=5\end{align*}$
::2 - 3y=5

$\begin{align*}2x+4y=2\end{align*}$
::2x+4y=2

$\begin{align*}(x-1)^2+y^2=1\end{align*}$
:x- 1) 2+y2=1

$\begin{align*}(x+3)^2+(y+3)^2=18\end{align*}$
:x+3)2+(y+3)2=18

$\begin{align*}y=7\end{align*}$
::y=7 y=7

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

矩形到极地转换

Converting Rectangular Coordinates to Polar Coordinates ::将矩形坐标转换为极坐标

Converting Coordinates ::转换坐标

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Converting Rectangular Coordinates to Polar Coordinates
::将矩形坐标转换为极坐标

Converting Coordinates
::转换坐标

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)