课程： 6.6 赤道的矩形至极极表

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节方形矩形至极形矩形

折叠展开
方形矩形至极形矩形
You are working diligently in your math class when your teacher gives you an equation to graph:
::当你的老师给了你一个方程式图时, 你在数学课上勤奋工作:

$\begin{aligned} (x + 1)^{2} - (y + 2)^{2} = 7 \end{aligned}$
:x+1)2-(y+2)2=7

As you start to consider how to rearrange this equation, you are told that the goal of the class is to convert the equation to polar form instead of rectangular form .
::当您开始考虑如何重新排列这个方程时, 被告知该类的目标是将方程转换为极形, 而不是矩形。

Can you find a way to do this?
::你能想个办法吗?

Rectangular Equations to Polar Form
::极形矩形方形方形对极形方形的矩形方形

Interestingly, a rectangular coordinate system isn't the only way to plot values. A polar system can be useful. However, it will often be the case that there are one or more equations that need to be converted from rectangular to polar form. To write a rectangular equation in polar form, the conversion equations of $\begin{aligned} x = r \cos θ \end{aligned}$ and $\begin{aligned} y = r \sin θ \end{aligned}$ are used.
::有趣的是, 矩形坐标系统不是绘制值的唯一方法。极地系统可能有用。但是, 通常会出现一个或一个以上的方程式需要从矩形转换为极形的情况。要以极形写成矩形方程式, 则使用 x=rcos 和 y=rsin 的转换方程式。

If the graph of the polar equation is the same as the graph of the rectangular equation, then the conversion has been determined correctly.
::如果极方方程式的图形与矩形方程式的图形相同,则转换被正确确定。

$\begin{aligned} (x - 2)^{2} + y^{2} = 4 \end{aligned}$

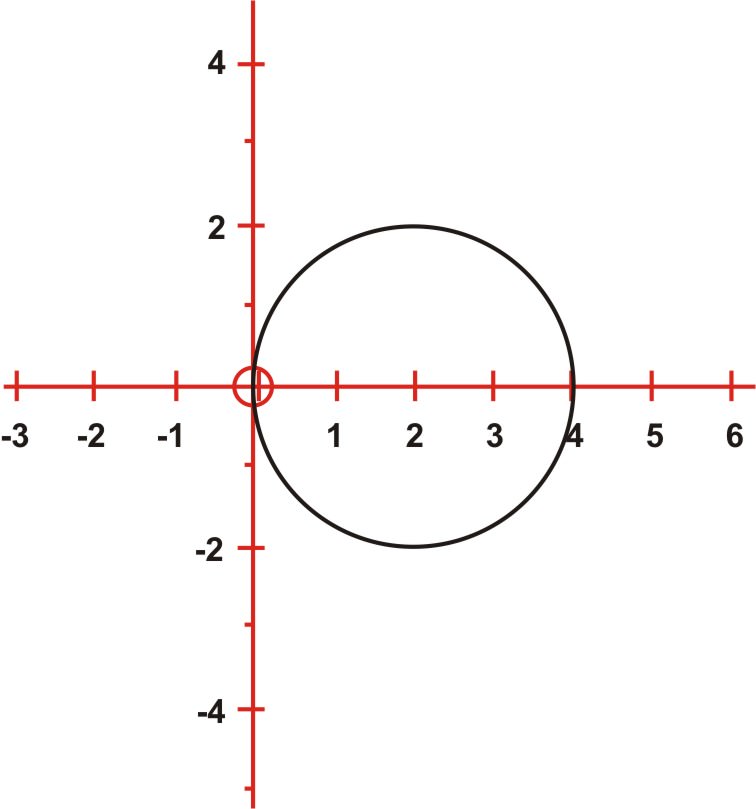
:x-2)2+y2=4

The rectangular equation $\begin{aligned} (x - 2)^{2} + y^{2} = 4 \end{aligned}$ represents a circle with center (2, 0) and a radius of 2 units. The polar equation $\begin{aligned} r = 4 \cos θ \end{aligned}$ is a circle with center (2, 0) and a radius of 2 units.
::矩形方程式 (x-2) 2+y2=4 表示圆,中间为 2, 0,半径为 2 个单位。极方程式 r= 4cos是一个圆,中间为 2, 0 个单位, 半径为 2 个单位。

Converting Equations
::转换等号

1. Write the rectangular equation $\begin{aligned} x^{2} + y^{2} = 2 x \end{aligned}$ in polar form.
::1. 以极形写成矩形方程式x2+y2=2x。

Remember $\begin{aligned} r = \sqrt{x^{2} + y^{2}}, r^{2} = x^{2} + y^{2} \end{aligned}$ and $\begin{aligned} x = r \cos θ \end{aligned}$ .
::记住 r=x2+y2,r2=x2+y2和 x=rcos。

$\begin{aligned} x^{2} + y^{2} & = 2 x \\ r^{2} & = 2 (r \cos θ) & P y t h a g o r e a n T h e o r e m a n d x = r \cos θ \\ r^{2} & = 2 r \cos θ \\ r & = 2 \cos θ & D i v i d e e a c h s i d e b y r \end{aligned}$

::x2+y2=2xr2=2(rcos)

2. Write $\begin{aligned} (x - 2)^{2} + y^{2} = 4 \end{aligned}$ in polar form.
::2. 以极地形式写(x-2)2+y2=4。

Remember $\begin{aligned} x = r \cos θ \end{aligned}$ and $\begin{aligned} y = r \sin θ \end{aligned}$ .
::记住 x=rcos和y=rsin。

$\begin{aligned} (x - 2)^{2} + y^{2} = 4 \\ (r \cos θ - 2)^{2} + (r \sin θ)^{2} = 4 & x = r \cos θ a n d y = r \sin θ \\ r^{2} \cos^{2} θ - 4 r \cos θ + 4 + r^{2} \sin^{2} θ = 4 & e x p a n d t h e t e r m s \\ r^{2} \cos^{2} θ - 4 r \cos θ + r^{2} \sin^{2} θ = 0 & s u b t r a c t 4 f r o m e a c h s i d e \\ r^{2} \cos^{2} θ + r^{2} \sin^{2} θ = 4 r \cos θ & i s o l a t e t h e s q u a r e d t e r m s \\ r^{2} (\cos^{2} θ + \sin^{2} θ) = 4 r \cos θ & f a c t o r r^{2} - a c o m m o n f a c t o r \\ r^{2} = 4 r \cos θ & P y t h a g o r e a n I d e n t i t y \\ r = 4 \cos θ & D i v i d e e a c h s i d e b y r \end{aligned}$

:x-2)2+y2=4(rcos%2)2+(rsin)2+(rsin)2=4x=rcos和y=rsinr2cos2\4+r2sin24Expl 以及每侧2cs24rcosr2sin224xy2=4(rsos%2)2+(rsin)2=4xrcos=rcos=r2rr2}4+r2sus_rcos%4+r2sin2_rsin22}22rcosr2r2rsr2r2rcos=4cos=divide by r

3. Write the rectangular equation $\begin{aligned} (x + 4)^{2} + (y - 1)^{2} = 17 \end{aligned}$ in polar form.
::3. 以极形写成矩形方程(x+4)2+(y-1)2=17。

$\begin{aligned} (x + 4)^{2} + (y - 1)^{2} = 17 \\ (r \cos θ + 4)^{2} + (r \sin θ - 1)^{2} = 17 & x = r \cos θ a n d y = r \sin θ \\ r^{2} \cos^{2} θ + 8 r \cos θ + 16 + r^{2} \sin^{2} θ - 2 r \sin θ + 1 = 17 & e x p a n d t h e t e r m s \\ r^{2} \cos^{2} θ + 8 r \cos θ - 2 r \sin θ + r^{2} \sin^{2} θ = 0 & s u b t r a c t 17 f r o m e a c h s i d e \\ r^{2} \cos^{2} θ + r^{2} \sin^{2} θ = - 8 r \cos θ + 2 r \sin θ & i s o l a t e t h e s q u a r e d t e r m s \\ r^{2} (\cos^{2} θ + \sin^{2} θ) = - 2 r (4 \cos θ - \sin θ) & f a c t o r r^{2} - a c o m m o n f a c t o r \\ r^{2} = - 2 r (4 \cos θ - \sin θ) & P y t h a g o r e a n I d e n t i t y \\ r = - 2 (4 \cos θ - \sin θ) & D i v i d e e a c h s i d e b y r \end{aligned}$

:x+4) 2+(y-1) 2=17(rcos1) 2+(rsin1) 2=17x=rcos和y=rsin_r2cos28rcos16+r2sin222rsin}1=17Explate 术语2cos28rcos2rsin20suptl17

Examples
::实例

Example 1
::例1

Earlier, you were asked to convert an equation to polar form.
::早些时候,你被要求将方程式转换成极形。

The original equation to convert is:
::要转换的原始方程式是:

$\begin{aligned} (x + 1)^{2} - (y + 2)^{2} = 7 \end{aligned}$
:x+1)2-(y+2)2=7

You can substitute $\begin{aligned} x = r \cos θ \end{aligned}$ and $\begin{aligned} y = r \sin θ \end{aligned}$ into the equation, and then simplify:
::您可以在方程中替换 x=rcos和y=rsin, 然后简化 :

$\begin{aligned} (r \cos θ + 1)^{2} - (r \sin θ + 2)^{2} = 7 \\ (r^{2} \cos^{2} θ + 2 r \cos θ + 1) - (r^{2} \sin^{2} θ + 4 r \sin θ + 4) = 7 \\ r^{2} (\cos^{2} θ - \sin^{2} θ) + 2 r (\cos θ - 2 \sin θ) - 3 = 7 \\ r^{2} (\cos^{2} θ - \sin^{2} θ) + 2 r (\cos θ - 2 \sin θ) = 10 \end{aligned}$

:rcos%1) 2-(rsin%2) 2=7(r2cos2) 2-2(r2cos%1) -(r2sin2) 4) =7r2(cos2) sin2) +2r(cos%2sin) -3=7r2(cos2) sin2) +2r(cos%2sin) =10

Example 2
::例2

Write the rectangular equation $\begin{aligned} (x - 4)^{2} + (y - 3)^{2} = 25 \end{aligned}$ in polar form.
::以极度形式写入矩形方程 (x-4) 2+(y-3)2=25。

$\begin{aligned} (x - 4)^{2} + (y - 3)^{2} & = 25 \\ x^{2} - 8 x + 16 + y^{2} - 6 y + 9 & = 25 \\ x^{2} - 8 x + y^{2} - 6 y + 25 & = 25 \\ x^{2} - 8 x + y^{2} - 6 y & = 0 \\ x^{2} + y^{2} - 8 x - 6 y & = 0 \\ r^{2} - 8 (r \cos θ) - 6 (r \sin θ) & = 0 \\ r^{2} - 8 r \cos θ - 6 r \sin θ & = 0 \\ r (r - 8 \cos θ - 6 \sin θ) & = 0 \\ r = 0 or r - 8 \cos θ - 6 \sin θ & = 0 \\ r = 0 or r & = 8 \cos θ + 6 \sin θ \end{aligned}$

:x-4)2+2+(y-3)2=25x2-8x6x6y+9=25x2-8x+y2-6y+25=25x2-8x+y2-6y=0x2+y2-8x-6y=0r2-8(rcos)-6(rsin)=0r2-8rcos_8rcs%6rsin0r(r-8cos6sin)=0r=0或r-8cos_6sin0r=0或r=8cos_6sin}

From graphing $\begin{aligned} r - 8 \cos θ - 6 \sin θ = 0 \end{aligned}$ , we see that the additional solutions are 0 and 8.
::从图表 r -8cos\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\8\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\8\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Example 3
::例3

Write the rectangular equation $\begin{aligned} 3 x - 2 y = 1 \end{aligned}$ in polar form.
::以极形写入矩形方程式 3x--2y=1。

$\begin{aligned} 3 x - 2 y & = 1 \\ 3 r \cos θ - 2 r \sin θ & = 1 \\ r (3 \cos θ - 2 \sin θ) & = 1 \\ r & = \frac{1}{3 \cos θ - 2 \sin θ} \end{aligned}$

::3x-2y=13rcos2rsin1r(3cos2sin)=1r=13cos2sin1r

Example 4
::例4

Write the rectangular equation $\begin{aligned} x^{2} + y^{2} - 4 x + 2 y = 0 \end{aligned}$ in polar form.
::以极形写入矩形方程式 x2+y2-4x+2y=0。

$\begin{aligned} x^{2} + y^{2} - 4 x + 2 y & = 0 \\ r^{2} \cos^{2} θ + r^{2} \sin^{2} θ - 4 r \cos θ + 2 r \sin θ & = 0 \\ r^{2} (\sin^{2} θ + \cos^{2} θ) - 4 r \cos θ + 2 r \sin θ & = 0 \\ r (r - 4 \cos θ + 2 \sin θ) & = 0 \\ r = 0 or r - 4 \cos θ + 2 \sin θ & = 0 \\ r = 0 or r & = 4 \cos θ - 2 \sin θ \end{aligned}$

::x2+y2 - 4x+2y=0r2r2cos2r2sin24rcos%2rsin0r2(sin22cos2)-4rcos%2rsin0r(r-4cos%2sin)=0r=0或r-4cos%2sin=0或r=4cos%0r=0或r=4cos%2sin}

Review
::回顾

Write each rectangular equation in polar form.
::将每个矩形方程写成极形。

$\begin{aligned} x = 3 \end{aligned}$
::x=3x=3

$\begin{aligned} y = 4 \end{aligned}$
::y=4 y=4

$\begin{aligned} x^{2} + y^{2} = 4 \end{aligned}$
::x2+y2=4 x2+y2=4

$\begin{aligned} x^{2} + y^{2} = 9 \end{aligned}$
::x2+y2=9

$\begin{aligned} (x - 1)^{2} + y^{2} = 1 \end{aligned}$
:x- 1) 2+y2=1

$\begin{aligned} (x - 2)^{2} + (y - 3)^{2} = 13 \end{aligned}$
:x-2)2+(y-3)2=13

$\begin{aligned} (x - 1)^{2} + (y - 3)^{2} = 10 \end{aligned}$
:x-1)2+(y-3)2=10

$\begin{aligned} (x + 2)^{2} + (y + 2)^{2} = 8 \end{aligned}$
:x+2)2+(y+2)2=8

$\begin{aligned} (x + 5)^{2} + (y - 1)^{2} = 26 \end{aligned}$
:x+5)2+(y-1)2=26

$\begin{aligned} x^{2} + (y - 6)^{2} = 36 \end{aligned}$
::x2+(y-6)2=36

$\begin{aligned} x^{2} + (y + 2)^{2} = 4 \end{aligned}$
::x2+(y+2)2=4

$\begin{aligned} 2 x + 5 y = 11 \end{aligned}$
::2x+5y=11

$\begin{aligned} 4 x - 7 y = 10 \end{aligned}$
::4-7y=10

$\begin{aligned} x + 5 y = 8 \end{aligned}$
::x+5y=8 x+5y=8

$\begin{aligned} 3 x - 4 y = 15 \end{aligned}$
::3x-4y=15

Review (Answers)
::回顾(答复)

To see the Review answers, open this and look for section 6.6.
::阅读审查的答案,打开这一答案并查看第6.6节。

章节大纲

常规

方形矩形至极形矩形

Rectangular Equations to Polar Form ::极形矩形方形方形对极形方形的矩形方形

Converting Equations ::转换等号

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Rectangular Equations to Polar Form
::极形矩形方形方形对极形方形的矩形方形

Converting Equations
::转换等号

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)