Course: 6.8 等效极极曲线

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 等等极极曲线

Collapse Expand
等等极极曲线
While working on a problem in math class, you get a solution with a certain equation. In this case, your solution is $\begin{aligned} 3 + 2 \cos (θ) \end{aligned}$ . Your friend comes over and tells you that he thinks he has solved the problem. However, when he shows you his paper, his equation looks different from yours. His solution is $\begin{aligned} - 3 + 2 \cos (- θ) \end{aligned}$ . Is there a way you can determine if the two equations are equivalent?
::在数学课上遇到问题时, 您可以用一定的方程找到一个解决方案。在这种情况下, 您的解决方案是 3+2cos{{{{{{}}。您的朋友过来告诉你, 他认为他已经解决问题了。但是, 当您看到您的纸时, 您的方程与您的不同。您的解决方案是 3+2cos}}}}。您有办法确定这两个方程是否相等吗 ?

Equivalent Polar Curves
::等等极极曲线

The expression “same only different” comes into play in this section. We will graph two distinct polar equations that will produce two equivalent graphs. Use your graphing calculator and create these curves as the equations are presented.
::本节使用“相同不同”的表达式。我们将绘制两个截然不同的极方方程式, 产生两个等同的图形。使用您的图形计算器, 并在方程式显示时创建这些曲线。

In some other section, graphs were generated of a limaçon, a dimpled limaçon, a looped limaçon and a cardioid. All of these were of the form $\begin{aligned} r = a \pm b \sin θ \end{aligned}$ or $\begin{aligned} r = a \pm b \cos θ \end{aligned}$ . The easiest way to see what polar equations produce equivalent curves is to use either a graphing calculator or a software program to generate the graphs of various polar equations.
::在其他一些章节中,图表来自一个利马松、一个浸泡的里马松、一个环状的里马松和一个心血管,所有这些都是表单 r=absin 或 r=abcos。最容易看到极地方程式产生等值曲线的方法是使用图形计算器或软件程序来生成各种极地方程的图形。

Comparing Graphs of Polar Equations
::极赤道比较图

Plot the following polar equations and compare the graphs.
::绘制以下极方程式并比较图表。

$\begin{aligned} r & = 1 + 2 \sin θ \\ r & = - 1 + 2 \sin θ \end{aligned}$

::r=1+2sinr1+2sin

By looking at the graphs, the result is the same. So, even though $\begin{aligned} a \end{aligned}$ is different in both, they have the same graph. We can assume that the sign of $\begin{aligned} a \end{aligned}$ does not matter.
::通过查看图表,结果是一样的。因此,即使两者中有一个不同,它们也有相同的图表。我们可以假设一个符号无关紧要。

$\begin{aligned} r & = 4 \cos θ \\ r & = 4 \cos (- θ) \end{aligned}$

::r=4cosr=4cos()

These functions also result in the same graph. Here, $\begin{aligned} θ \end{aligned}$ differed by a negative. So we can assume that the sign of $\begin{aligned} θ \end{aligned}$ does not change the appearance of the graph.
::这些函数也产生相同的图形。这里, __ 以负值不同。所以我们可以假设 __ 的符号不会改变图形的外观。

Describing Graphs
::描述图表

1. Graph the equations $\begin{aligned} x^{2} + y^{2} = 16 \end{aligned}$ and $\begin{aligned} r = 4 \end{aligned}$ . Describe the graphs.
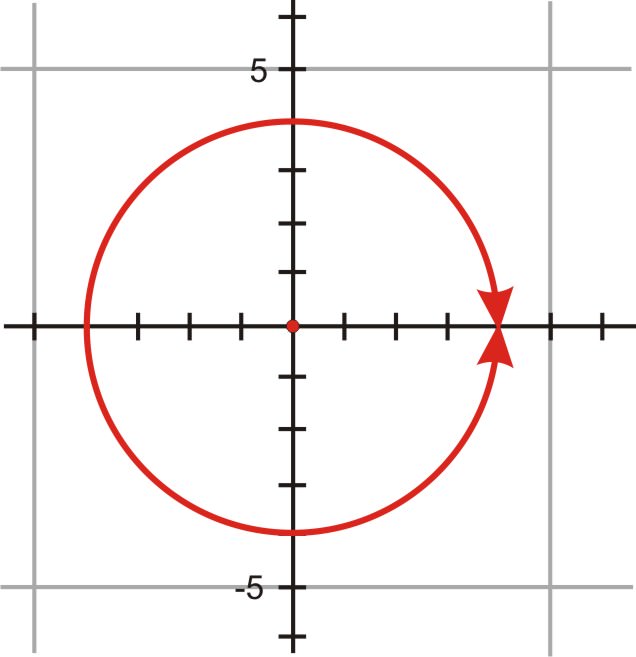
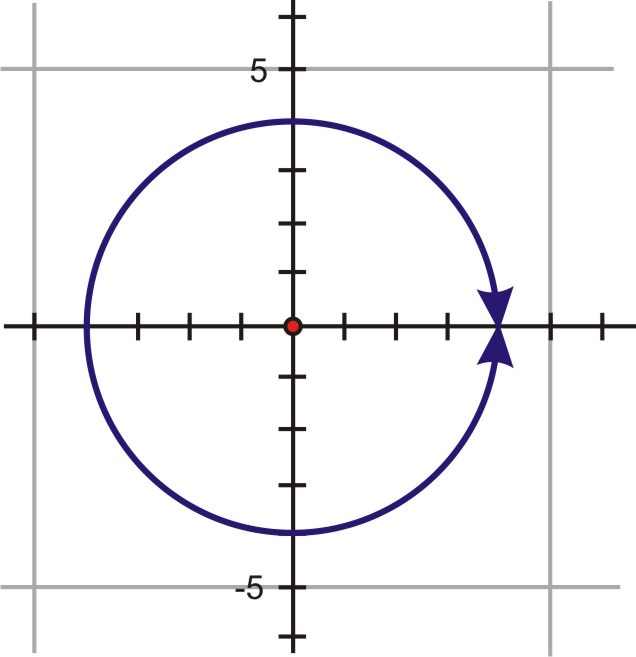
::1. 绘制方程式x2+y2=16和r=4。描述图表。

Both equations, one in rectangular form and one in polar form , are circles with a radius of 4 and center at the origin.
::两个方程,一个以矩形形式,一个以极形形式,都是圆形,半径为4,以原为中心。

2. Graph the equations $\begin{aligned} (x - 2)^{2} + (y + 2)^{2} = 8 \end{aligned}$ and $\begin{aligned} r = 4 \cos θ - 4 \sin θ \end{aligned}$ . Describe the graphs.
::2. 图解方程(x-2)2+(y+2)2=8和r=4cos=4sin。请描述图表。

There is not a visual representation shown here, but on your calculator you should see that the graphs are circles centered at (2, -2) with a radius $\begin{aligned} 2 \sqrt{2} \approx 2.8 \end{aligned}$ .
::这里没有显示视觉显示, 但是在您的计算器上, 您应该看到图表是圆形的, 以 2, 2 和 2 为中心, 半径为 22 2. 8 。

Examples
::实例

Example 1
::例1

Earlier, you were asked if there is a way you can determine if the two equations are equivalent.
::早些时候,有人问您是否有办法确定这两个方程是否等同。

As you learned in this section, we can compare graphs of equations to see if the equations are the same or not.
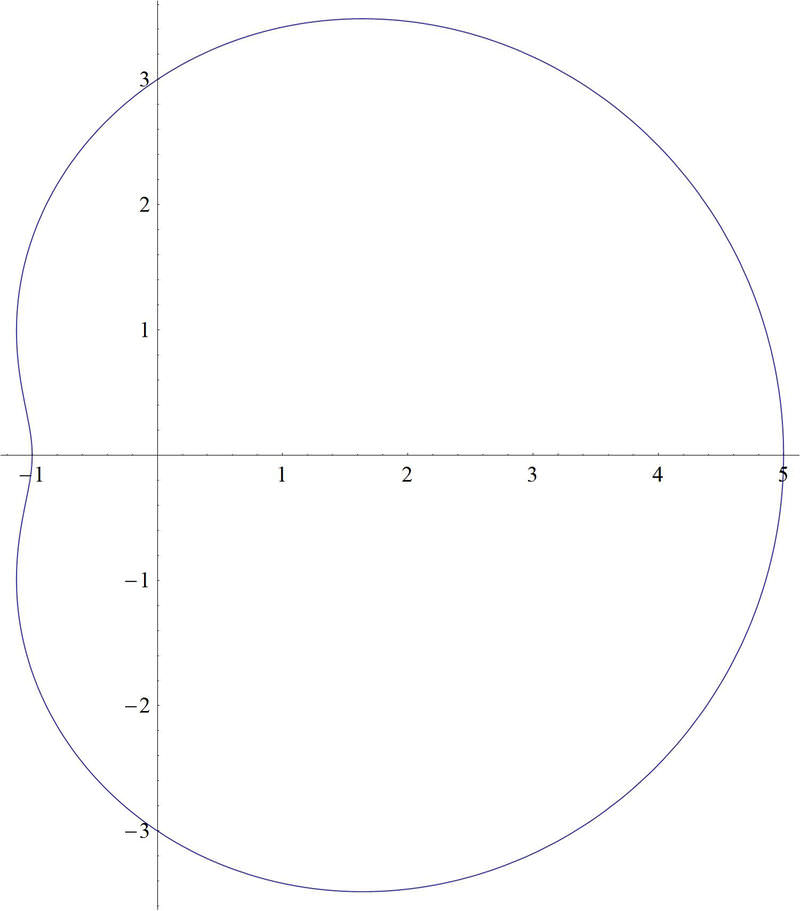
::正如你们在本节中所学到的, 我们可以比较方程式的图表, 看看方程式是否相同。

A graph of $\begin{aligned} 3 + 2 \cos (θ) \end{aligned}$ looks like this:
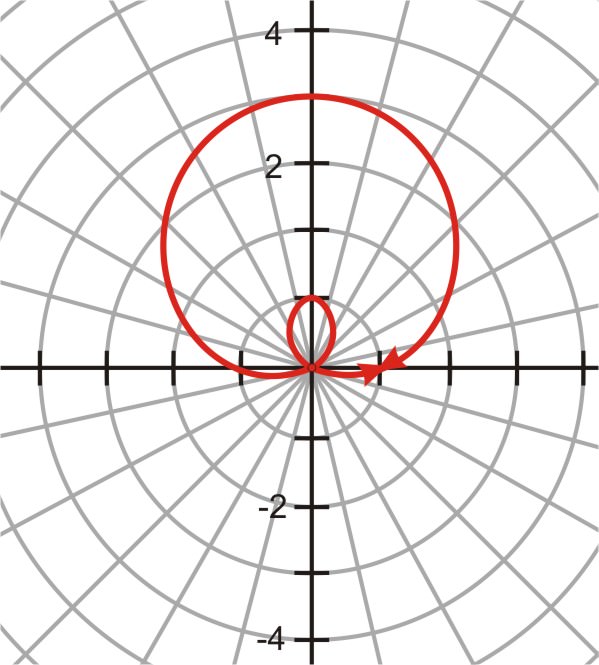
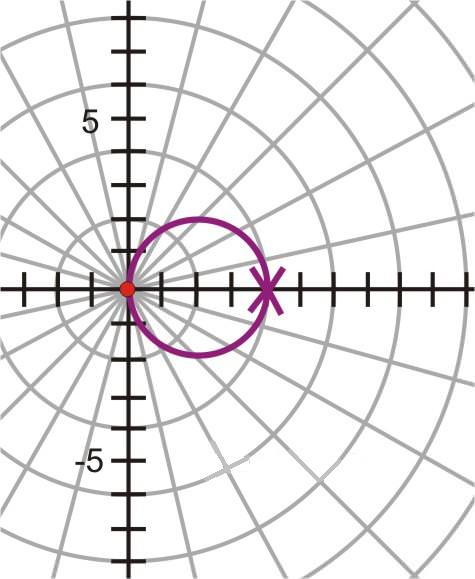
::3+2cos() 的图表看起来是这样 :

And a graph of $\begin{aligned} - 3 + 2 \cos (- θ) \end{aligned}$ looks like this:
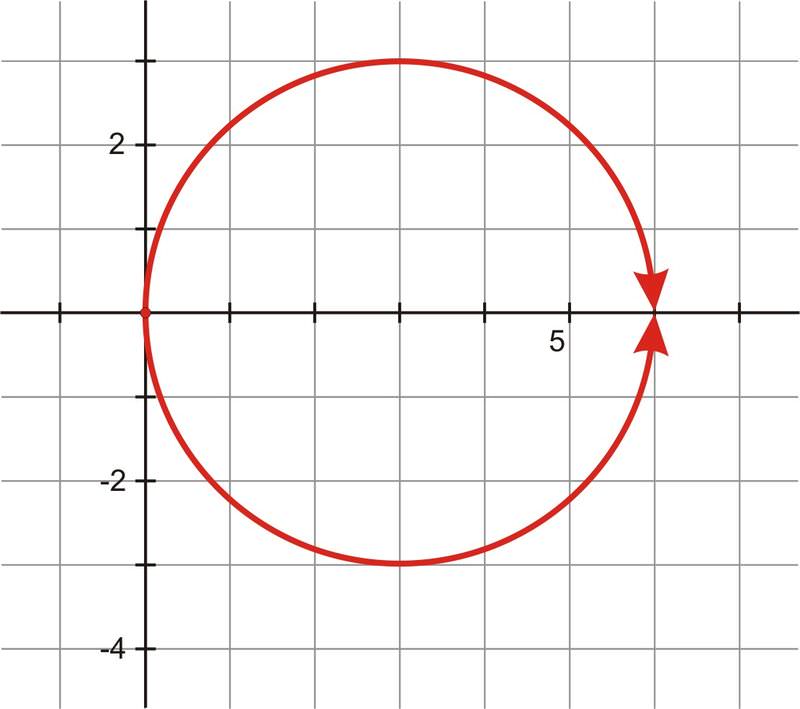
::3+2cos()的图象是这样的:

As you can see from the plots, your friend is correct. Your graph and his are the same, therefore the equations are equivalent.
::从图中可以看出,你的朋友是正确的。你的图表和他相同,所以方程式是等量的。

Example 2
::例2

Write the rectangular equation $\begin{aligned} x^{2} + y^{2} = 6 x \end{aligned}$ in polar form and graph both equations. Should they be equivalent?
::以极形写成矩形方程式 x2+y2=6x, 并用图形显示两个方程式。它们是否相等 ?

$\begin{aligned} x^{2} + y^{2} & = 6 x \\ r^{2} & = 6 (r \cos θ) & r^{2} = x^{2} + y^{2} and x = y \cos θ \\ r & = 6 \cos θ & divide by r \end{aligned}$

::x2+y2=6xr2=6(rcos)r2=x2+y2和 x=ycosr=6cosdivide by r

Both equations produced a circle with center $\begin{aligned} (3, 0) \end{aligned}$ and a radius of $\begin{aligned} 3 \end{aligned}$ .
::两个方程式产生了一个圆形,中间为3,0,半径为3。

Example 3
::例3

Determine if $\begin{aligned} r = - 2 + \sin θ \end{aligned}$ and $\begin{aligned} r = 2 - \sin θ \end{aligned}$ are equivalent without graphing.
::确定 r% 2+sin 和 r=2-sin 是否等同而没有图形化。

$\begin{aligned} r = - 2 + \sin θ \end{aligned}$ and $\begin{aligned} r = 2 - \sin θ \end{aligned}$ are not equivalent because the sine has the opposite sign. $\begin{aligned} r = - 2 + \sin θ \end{aligned}$ will be primarily above the horizontal axis and $\begin{aligned} r = 2 - \sin θ \end{aligned}$ will be mostly below. However, the two do have the same pole axis intercepts.
::r+2+sin和r=2-sin不等同,因为正弦有相反的符号。 r+2+sin将主要在水平轴上方, r=2-sin将主要在水平轴上方。但是, 两者有相同的极轴拦截。

Example 4
::例4

Determine if $\begin{aligned} r = - 3 + 4 \cos (- π) \end{aligned}$ and $\begin{aligned} r = 3 + 4 \cos π \end{aligned}$ are equivalent without graphing.
::确定 r+3+4cos 和 r=3+4cos是否等值, 而不显示图形。

$\begin{aligned} r = - 3 + 4 \cos (- π) \end{aligned}$ and $\begin{aligned} r = 3 + 4 \cos π \end{aligned}$ are equivalent because the sign of "a" does not matter, nor does the sign of $\begin{aligned} θ \end{aligned}$ .
::r3+4cos()和r=3+4cos是等效的,因为“a”的符号无关紧要,“a”的符号也无关紧要。

Review
::回顾

For each equation in rectangular form given below, write the equivalent equation in polar form.
::下文以矩形形式列出的每个方程,以极形形式写出等值方程。

$\begin{aligned} x^{2} + y^{2} = 4 \end{aligned}$
::x2+y2=4 x2+y2=4

$\begin{aligned} x^{2} + y^{2} = 6 y \end{aligned}$
::x2+y2=6y

$\begin{aligned} (x - 1)^{2} + y^{2} = 1 \end{aligned}$
:x- 1) 2+y2=1

$\begin{aligned} (x - 4)^{2} + (y - 1)^{2} = 17 \end{aligned}$
:x-4)2+(y-1)2=17

$\begin{aligned} x^{2} + y^{2} = 9 \end{aligned}$
::x2+y2=9

For each equation below in polar form, write another equation in polar form that will produce the same graph.
::对于下方的每个极形方程式,请写出另一个极形方程式,该方程式将产生相同的图形。

$\begin{aligned} r = 4 + 3 \sin θ \end{aligned}$
::r=4+3sin

$\begin{aligned} r = 2 - \sin θ \end{aligned}$
::r=2-sin

$\begin{aligned} r = 2 + 2 \cos θ \end{aligned}$
::r=2+2cos

$\begin{aligned} r = 3 - \cos θ \end{aligned}$
::r=3-cos

$\begin{aligned} r = 2 + \sin θ \end{aligned}$
::r=2+sin

Determine whether each of the following sets of equations produce equivalent graphs without graphing.
::确定以下各组方程式是否产生等效图,而不绘制图表。

$\begin{aligned} r = 3 - \sin θ \end{aligned}$ and $\begin{aligned} r = 3 + \sin θ \end{aligned}$
::r=3-sin和r=3+sin

$\begin{aligned} r = 1 + 2 \sin θ \end{aligned}$ and $\begin{aligned} r = - 1 + 2 \sin θ \end{aligned}$
::r=1+2sin和r1+2sin

$\begin{aligned} r = 3 \sin θ \end{aligned}$ and $\begin{aligned} r = 3 \sin (- θ) \end{aligned}$
::r=3sin和r=3sin()

$\begin{aligned} r = 2 \cos θ \end{aligned}$ and $\begin{aligned} r = 2 \cos (- θ) \end{aligned}$
::r=2cos和r=2cos()

$\begin{aligned} r = 1 + 3 \cos θ \end{aligned}$ and $\begin{aligned} r = 1 - 3 \cos θ \end{aligned}$
::r=1+3cos和r=1-3cos

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

等等极极曲线

Equivalent Polar Curves ::等等极极曲线

Comparing Graphs of Polar Equations ::极赤道比较图

Describing Graphs ::描述图表

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Equivalent Polar Curves
::等等极极曲线

Comparing Graphs of Polar Equations
::极赤道比较图

Describing Graphs
::描述图表

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)