课程： 6.15 复杂根的几何

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节复杂根的几何

折叠展开
复杂根的几何
You've just finished a problem where you needed to solve the equation:
::你刚刚解决了一个问题需要解决这个方程式

$\begin{align*}x^4 = 16\end{align*}$
::x4=16

After solving for the roots, which were $\begin{align*}2,-2,2i,-2i\end{align*}$ your instructor asks you to plot them on the complex plane .
::在解决了2-2,2,2i,2i的根后, 你的老师请你在复杂的平面上绘制这些根。

Can you accomplish this?
::你能做到吗?

Geometry of Complex Roots
::复杂根的几何

It's always good to get an intuitive feel for values by plotting them. This tendency extends into as well.
::通过勾画这些价值观来获得对价值观的直觉感觉总是一件好事。这种倾向也扩展到了。

The five roots of the equation $\begin{align*}x^5 - 32 = 0\end{align*}$ involve one real root and four complex ones. Let's take a look at a plot of these roots in the complex plane.
::等式的五个根 x5-32=0 涉及一个真正的根和四个复杂的根。让我们来看看这些根在复杂的平面上的图。

The $\begin{align*}n^{th}\end{align*}$ roots of a complex number , when graphed on the complex plane, are equally spaced around a circle. So, instead of having all the roots, all that is necessary to graph the roots is one of them and the radius of the circle. For this particular example, the roots are $\begin{align*}\frac{2\pi}{5}\end{align*}$ or $\begin{align*}72^\circ\end{align*}$ apart. This goes along with what we know about regular pentagons. The roots are $\begin{align*}\frac{2\pi}{n}\end{align*}$ degrees apart.
::复数的 nw 根, 当在复杂的平面上绘制图形时, 其正弦在圆圈上被同样地标出。因此, 与其将所有根都标出, 用来绘制根的所需要的只是其中的一个, 以及圆圈的半径。对于这个特定的例子, 根是 2°5 或 72 。这与我们所了解的关于普通五边形的情况是相同的。根是 2° 的。

Let's take a look at some problems involving the geometry of complex roots.
::让我们来研究一些复杂的根的几何学问题。

1. Calculate the two roots for $\begin{align*}x^2 = 1\end{align*}$ and represent them graphically.
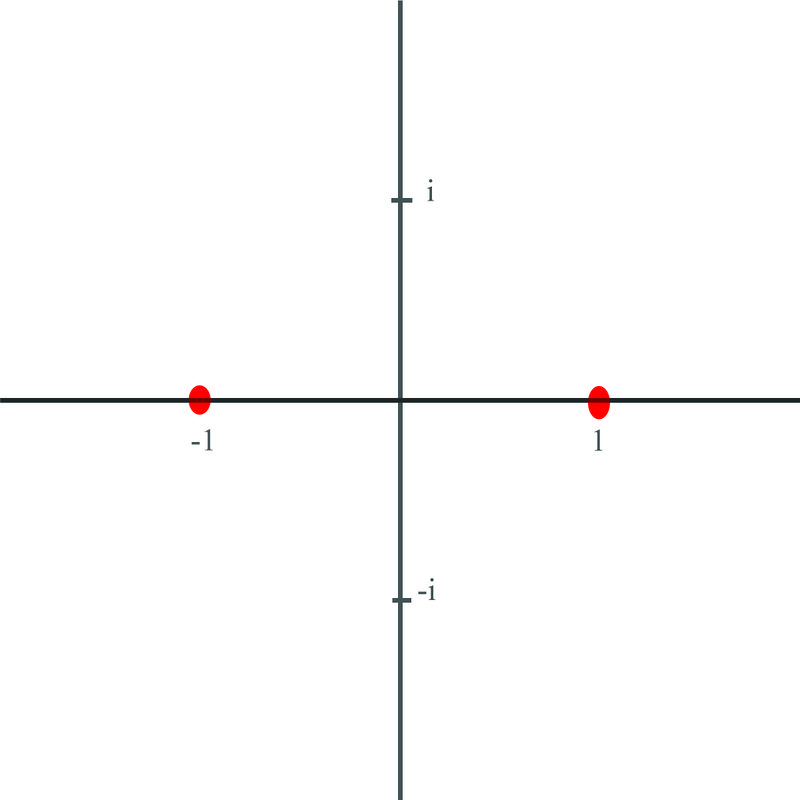
::1. 为 x2=1 计算两个根并用图形表示。

$\begin{aligned} x^{2} = 1 \\ r & = \sqrt{x^{2} + y^{2}} \\ r & = \sqrt{(1)^{2} + (0)^{2}} \\ r & = 1 \\ θ & = \tan^{- 1} (\frac{0}{1}) = 0 \end{aligned}$
$\begin{align*}x^2 = 1\\ r &= \sqrt{x^2+y^2}\\ r &= \sqrt{(1)^2+(0)^2}\\ r &= 1\\ \theta &= \tan^{-1} \left(\frac{0}{1}\right)=0\end{align*}$
::x2=1r=x2+y2r=(1)2+(0)2r=1}111(01)=0

Write an expression for determining the two roots of $\begin{align*}1 = 1 + 0i\end{align*}$
::写入用于确定 1=1+0i 两个根的表达式

$\begin{aligned} 1^{\frac{1}{2}} & = [1 (\cos (0 + 2 π k) + i \sin (0 + 2 π k)]^{\frac{1}{2}} \\ = 1 (\cos \frac{2 π k}{2} + i \sin \frac{2 π k}{2}) k = 0, 1 \\ x_{1} & = 1 (\cos \frac{0}{2} + i \sin \frac{0}{2}) \to 1 (\cos 0 + i \sin 0) = 1 & f o r k = 0 \\ x_{2} & = 1 (\cos \frac{2 π}{2} + i \sin \frac{2 π}{2}) = - 1 & f o r k = 1 \end{aligned}$
$\begin{align*}1^{\frac{1}{2}} &= [1( \cos (0+2\pi k)+i \sin (0+2\pi k)]^{\frac{1}{2}}\\ &= 1\left(\cos \frac{2\pi k}{2}+i \sin \frac{2\pi k}{2}\right)k=0, 1\\ x_1 &= 1\left(\cos \frac{0}{2}+i \sin \frac{0}{2}\right) \rightarrow 1(\cos 0 +i \sin 0)= 1 && for \ k=0\\ x_2 &= 1\left(\cos \frac{2\pi}{2}+i \sin \frac{2\pi}{2}\right) = -1 && for \ k=1\\ \end{align*}$
::112=[1(cos(0+2k)+isin(0+2k)]12=1(cos22K2+isin22k2k2k=0,1x1=1(cos02+isin02))\1(cos0+isin0)=1k=0x2=1(cos22+isin22)\1=1(k=1)

These roots are plotted here:
::这些根根是在这里绘制的:

2. Calculate the three roots for $\begin{align*}x^3 = 1\end{align*}$ and represent them graphically.
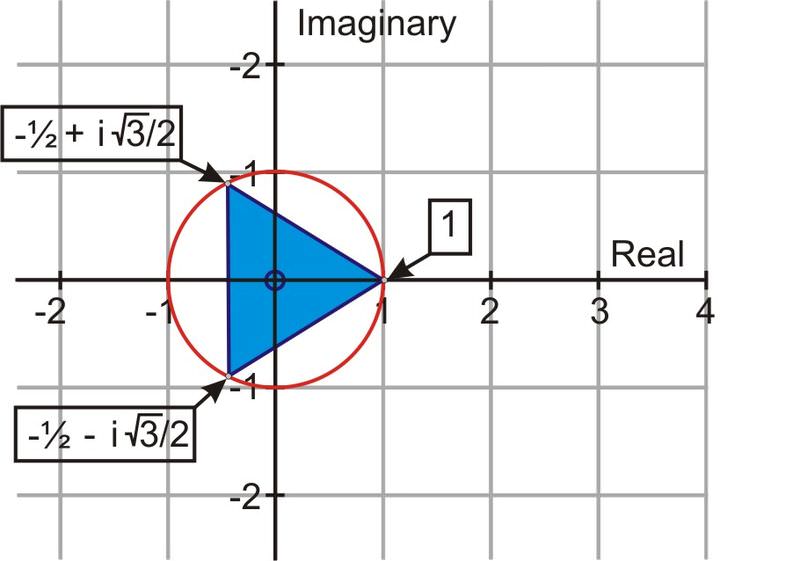
::2. 计算 x3=1 的三个根并用图形表示。

In standard form, $\begin{align*}1 = 1 + 0i \ r = 1\end{align*}$ and $\begin{align*}\theta = 0\end{align*}$ . The polar form is $\begin{align*}1 + 0i = 1 [\cos (0 + 2\pi k) + i \sin (0 + 2\pi k)]\end{align*}$ . The expression for determining the cube roots of $\begin{align*}1 + 0i\end{align*}$ is:
::在标准格式中, 1=1+0i r=1 和 0。极形为 1+0i=1 [cos( 0+2k)+isin( 0+2k)]。用于确定 1+0i 的立方根的表达式为 :

$\begin{aligned} (1 + 0 i)^{\frac{1}{3}} = 1^{\frac{1}{3}} (\cos \frac{0 + 2 π k}{3} + i \sin \frac{0 + 2 π k}{3}) \end{aligned}$
$\begin{align*}(1+0i)^{\frac{1}{3}}=1^{\frac{1}{3}} \left(\cos \frac{0+2 \pi k}{3}+i \sin \frac{0+2 \pi k}{3} \right)\end{align*}$
:1+0i)13=113(cos=0+2k3+isin=0+2k3)

When $\begin{align*}k = 0, k = 1\end{align*}$ and $\begin{align*}k = 2\end{align*}$ the three cube roots of 1 are $\begin{align*}1, -\frac{1}{2}+i \frac{\sqrt{3}}{2}, -\frac{1}{2} -i \frac{\sqrt{3}}{2}\end{align*}$ . When these three roots are represented graphically, the three points, on the circle with a radius of 1 (the cubed root of 1 is 1), form a triangle.
::k=0, k=1 和 k=2 1 的3个立方根为 1, 即 1, - 12+i32, - 12- i32。当这三个根以图形方式表示时, 圆圆圆的3个点为 1 半径( 1 的立方根为 1) , 组成三角形。

3. Calculate the four roots for $\begin{align*}x^4 = 1\end{align*}$ and represent them graphically
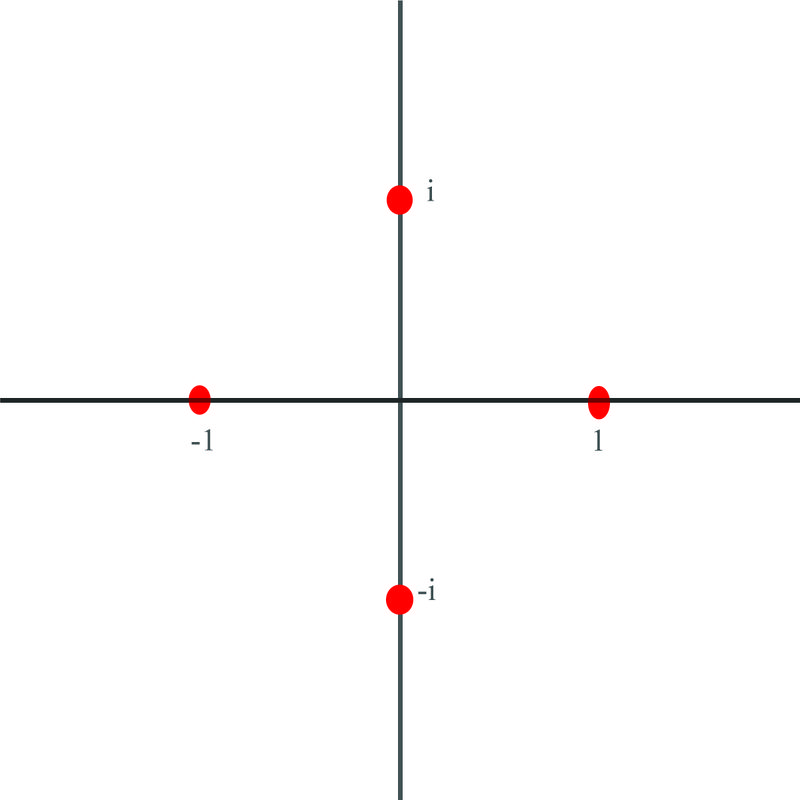
::3. 为 x4=1 计算四个根根,并用图形表示

$\begin{aligned} x^{4} = 1 \\ r & = \sqrt{x^{2} + y^{2}} \\ r & = \sqrt{(1)^{2} + (0)^{2}} \\ r & = 1 \\ θ & = \tan^{- 1} (\frac{0}{1}) = 0 \end{aligned}$
$\begin{align*}x^4 = 1\\ r &= \sqrt{x^2+y^2}\\ r &= \sqrt{(1)^2+(0)^2}\\ r &= 1\\ \theta &= \tan^{-1} \left(\frac{0}{1}\right)=0\end{align*}$
::x4=1r=x2+y2r=(1)2+(0)2r=1}111(01)=0

Write an expression for determining the cube roots of $\begin{align*}1 = 1 + 0i\end{align*}$
::写入用于确定 1=1+0i 的立方根的表达式

$\begin{aligned} 1^{\frac{1}{4}} & = [1 (\cos (0 + 2 π k) + i \sin (0 + 2 π k)]^{\frac{1}{4}} \\ = 1 (\cos \frac{2 π k}{4} + i \sin \frac{2 π k}{4}) k = 0, 1, 2, 3 \\ x_{1} & = 1 (\cos \frac{0}{4} + i \sin \frac{0}{4}) \to 3 (\cos 0 + i \sin 0) = 1 & f o r k = 0 \\ x_{2} & = 1 (\cos \frac{2 π}{4} + i \sin \frac{2 π}{4}) = 0 + i = i & f o r k = 1 \\ x_{3} & = 1 (\cos \frac{4 π}{4} + i \sin \frac{4 π}{4}) = - 1 - 0 i = - 1 & f o r k = 2 \\ x_{4} & = 1 (\cos \frac{6 π}{4} + i \sin \frac{6 π}{4}) = 0 - i = - i & f o r k = 3 \end{aligned}$
$\begin{align*}1^{\frac{1}{4}} &= [1( \cos (0+2\pi k)+i \sin (0+2\pi k)]^{\frac{1}{4}}\\ &= 1\left(\cos \frac{2\pi k}{4}+i \sin \frac{2\pi k}{4}\right)k=0, 1, 2, 3\\ x_1 &= 1\left(\cos \frac{0}{4}+i \sin \frac{0}{4}\right) \rightarrow 3(\cos 0 +i \sin 0)= 1 && for \ k=0\\ x_2 &= 1\left(\cos \frac{2\pi}{4}+i \sin \frac{2\pi}{4}\right) = 0 + i = i && for \ k=1\\ x_3 &= 1\left(\cos \frac{4\pi}{4}+i \sin \frac{4\pi}{4}\right) = -1 - 0i = -1 && for \ k=2\\ x_4 &= 1\left(\cos \frac{6\pi}{4}+i \sin \frac{6\pi}{4}\right) = 0 - i = -i && for \ k=3\\ \end{align*}$
::114=[1(cos0+2k)+isin(0+2k)]14=1(cos2K4+isin2K4)k=0,1,2,3x1=1(cos04+isin04)}}3(cos0+isin0)=1k=0x2=1(cos24+isin24)=0+i=if k=1x3=1(cos444+isin4}}1-0i1fk=2x4=1(cos64+isin64)=0-iifor k=3

These roots are plotted here:
::这些根根是在这里绘制的:

Examples
::实例

Example 1
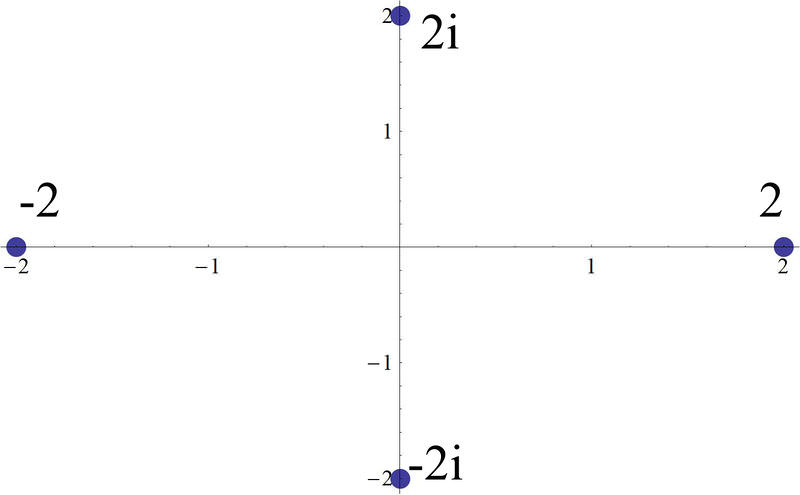
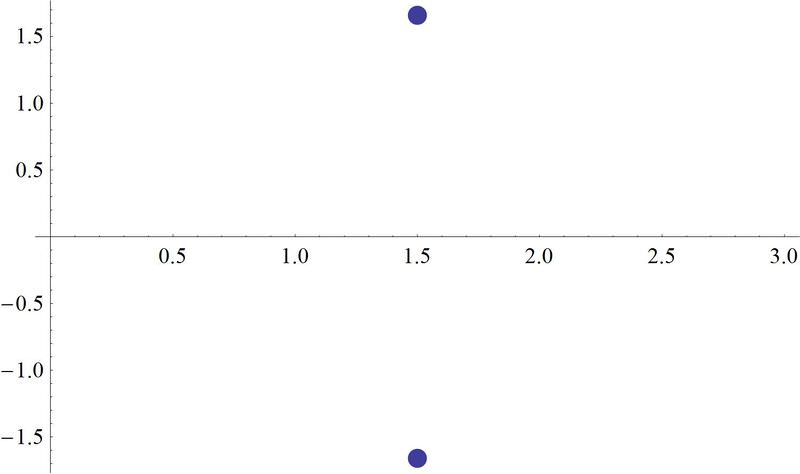
::例1

Earlier, you were asked to plot $\begin{align*}2,-2,2i,-2i\end{align*}$ on a plane.
::早些时候,你被要求在一架飞机上图2 -2,2i,2i。

You can see a plot of these roots here. Notice, as mentioned before, that the roots are placed equidistant around a circle that could be drawn in the plane with a radius of two.
::您可以在此看到这些根的图块。如前所述, 注意根部位于一个圆形的相等位置, 圆形可以在半径为2的平面上绘制。

Example 2
::例2

In the examples above, you saw the complex roots determined for a number of different polynomial orders, such as $\begin{align*}x^2, x^3, x^4\end{align*}$ . What conclusion can you draw about the number of complex roots there are in relation to the order of the polynomial being solved?
::在上述例子中, 您看到为一些不同的多元顺序( 如 x2, x3, x4) 所决定的复杂根根。您能够得出什么结论 ? 与所解决的多元型顺序相关的复杂根数 ?

You can conclude that the total number of roots is the same as the order of the polynomial under consideration. For example, $\begin{align*}x^2\end{align*}$ will have 2 roots, while $\begin{align*}x^3\end{align*}$ will have 3 roots, etc.
::您可以得出结论, 根的总数与审议中的多义的顺序相同。例如, x2 将有两个根, x3 将有三个根, 等等。

Example 3
::例3

What is the spacing in between the roots of the polynomial $\begin{align*}x^6 = 12\end{align*}$ ?
::多面形 x6=12 根之间的间距是多少 ?

Since there are six total roots, and all of the roots are equally spaced around a circle in the complex plane, there are $\begin{align*}\frac{360^\circ}{6} = 60^\circ\end{align*}$ between roots.
::由于共有6根根根,所有根在复杂的平面上一个圆圈上都一样,根间有3606=60。

Example 4
::例4

Solve for the roots of the equation $\begin{align*}x^2 - 3x + 5 = 0\end{align*}$ and plot them.
::解决方程式的根 x2- 3x+5=0 并绘制。

This equation can be solved using the familiar quadratic formula. Notice that previously we used quadratics that gave real solutions. However, there is no reason to limit the solution set to the real numbers, now that you know how to utilize as well.
::这个方程式可以用熟悉的二次方程式来解决。注意我们以前使用的二次方程式提供了真正的解决方案。但是, 没有理由将设定的解决方案限制在实际数字上, 既然你也知道如何使用。

$\begin{aligned} x = \frac{- (- 3) \pm \sqrt{(- 3)^{2} - (4) (1) (5)}}{(2) (1)} \\ = \frac{3 \pm \sqrt{- 11}}{2} \\ = \frac{3 \pm i \sqrt{11}}{2} \\ = \frac{3}{2} \pm \frac{i \sqrt{11}}{2} \end{aligned}$
$\begin{align*} x = \frac{-(-3) \pm \sqrt{(-3)^2-(4)(1)(5)}}{(2)(1)}\\ =\frac{3 \pm \sqrt{-11}}{2}\\ =\frac{3 \pm i\sqrt{11}}{2}\\ = \frac{3}{2} \pm \frac{i\sqrt{11}}{2}\\ \end{align*}$
::X(-3)-(-3)-(-3)-2(4)(1)(2)(1)=3112=31112=32i112

A plot of these roots looks like this:
::这些根的图象是这样的:

where the vertical axis is the line.
::垂直轴为直线。

Review
::回顾

How many roots does $\begin{align*}x^5=1\end{align*}$ have?
::x5=1 有多少根?

Calculate the roots of $\begin{align*}x^5=1\end{align*}$ and represent them graphically.
::计算 x5=1 的根并用图形表示。

How many roots does $\begin{align*}x^8=1\end{align*}$ have?
::x8=1 有多少根?

Calculate the roots of $\begin{align*}x^8=1\end{align*}$ and represent them graphically.
::计算 x8=1 的根并用图形表示。

How many roots does $\begin{align*}x^{10}=1\end{align*}$ have?
::x10=1 有多少根?

Calculate the roots of $\begin{align*}x^{10}=1\end{align*}$ and represent them graphically.
::计算 x10=1 的根并用图形表示。

How many roots does $\begin{align*}x^4=16\end{align*}$ have?
::x4=16 有多少根?

Calculate the roots of $\begin{align*}x^4=16\end{align*}$ and represent them graphically.
::计算 x4=16 的根并用图形表示。

How many roots does $\begin{align*}x^3=27\end{align*}$ have?
::x3=27 有多少根?

Calculate the roots of $\begin{align*}x^3=27\end{align*}$ and represent them graphically.
::计算 x3=27 的根并用图形表示。

How do the solutions of the equation $\begin{align*}x^3=-1\end{align*}$ compare to the solutions of the equation $\begin{align*}x^3=1\end{align*}$ ?
::公式 x3=1 的解决方案与公式 x3=1 的解决方案相比如何?

Describe how to represent the roots of $\begin{align*}x^6=1\end{align*}$ graphically without first solving the equation.
::描述如何用图形方式代表 x6=1 的根, 而不先解析方程。

Describe how to represent the roots of $\begin{align*}x^{12}=1\end{align*}$ graphically without first solving the equation.
::描述如何用图形方式代表 x12=1 的根, 而不先解析方程式。

Describe how to represent the roots of $\begin{align*}x^4=81\end{align*}$ graphically without first solving the equation.
::描述如何用图形方式代表 x4=81 的根, 而不先解析方程。

Describe how to represent the roots of $\begin{align*}x^8=256\end{align*}$ graphically without first solving the equation.
::描述如何用图形方式代表 x8=256 的根, 而不先解析方程。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

复杂根的几何

Geometry of Complex Roots ::复杂根的几何

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Geometry of Complex Roots
::复杂根的几何

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)