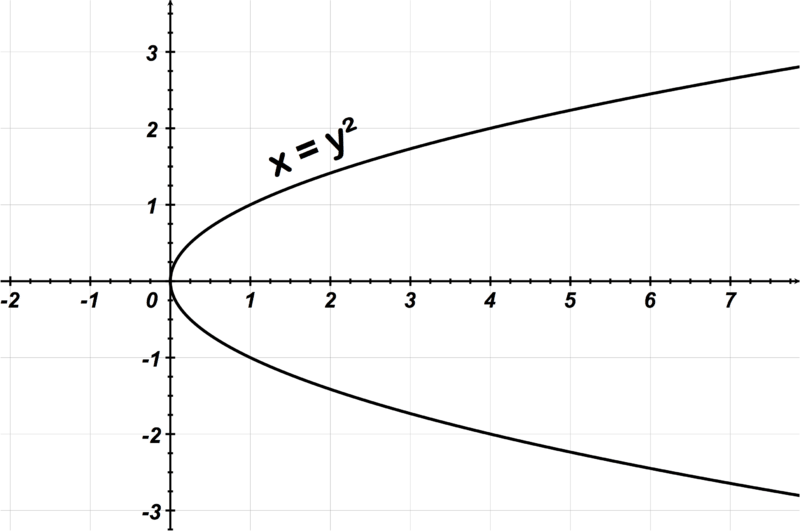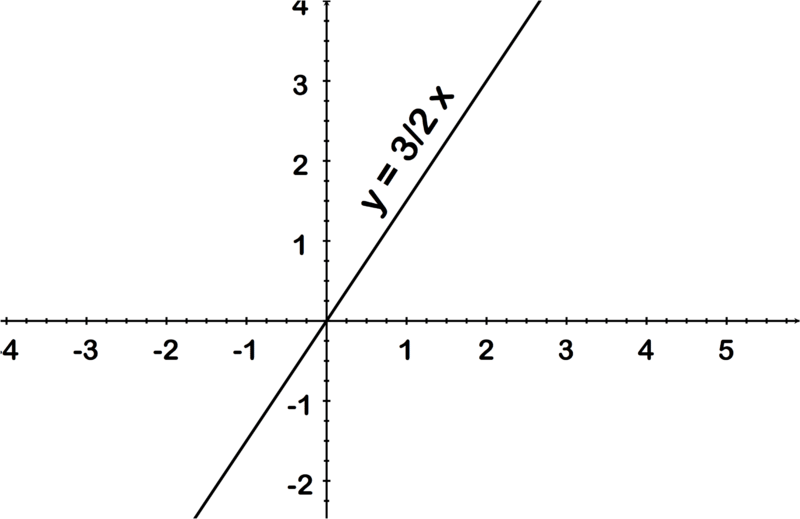Course: 1.1 关系和职能 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

关系和职能

Suppose you wanted to predict the cost of going to see a movie at the theater, you text a number of your friends who have seen movies recently to ask how much it cost them, here are the responses:
::假设你想预测去看电影的成本, 你发短信给最近看过电影的朋友, 问他们花了多少钱, 以下是回应:

"$14.50 "

"$8.75 + $3.50 for popcorn"
::"8.75美元+3.50美元的爆米花"

"five bucks - dollar theater"
::"五块钱 -一块钱剧院"

"$17.50 :'-( broke now"
::"17.50美元:" -(现在破了)"

"$12.75 loved the 3D!"
::"12.75美元爱3D!"

Can you accurately predict the cost of going to a movie from these responses? Why or why not?
::你能从这些回应中准确预测去看电影的成本吗?为什么或为什么?

Relations and Functions
::关系和职能

Consider two situations shown in the boxes below:
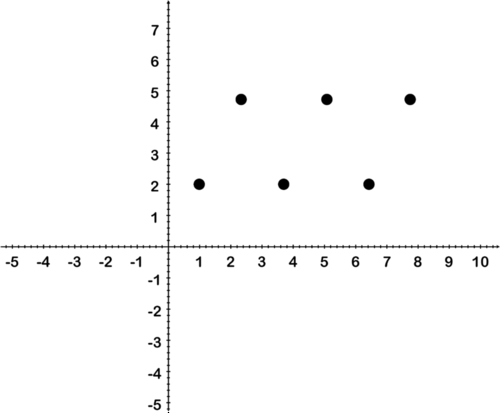
::考虑以下方框所示两种情况:

Situation 1: You are selling candy bars for a school fundraiser. Each candy bar costs $3.00	Situation 2: You collect data from several students in your class on their ages and their heights: (18,65"), (17,64"), (18,67"), (18,68"), (17,66")

In the first situation, let the variable $\begin{aligned} x \end{aligned}$ represent the number of candy bars that you sell, and let $\begin{aligned} y \end{aligned}$ represent the amount of money you make. If you sell $\begin{aligned} x \end{aligned}$ candy bars, you will make $\begin{aligned} y = 3 x \end{aligned}$ dollars. For example, if you sell 25 candy bars, you will make 3(25) = $75.00. Notice that you can use the number of candy bars you sell to predict how much money you will make.
::在第一种情况下,让变量 x 代表您出售的糖果棒的数量,让 Y 代表您挣的钱数量。如果您卖了糖果棒, 你会赚到 y= 3x 美元。例如, 如果你卖了 25 个糖果棒, 你会赚到 3( 25 ) = 75. 00 。请注意, 您可以使用您卖的糖果棒的数量来预测您能赚到多少钱。

Now consider the second situation. Can you similarly use the data to predict specific height, based on age?
::现在考虑第二个情况。您可以同样使用这些数据来预测特定高度, 以年龄为基础吗 ?

No, this is not the case in the second situation. For example, if a student is 18 years old, there are several heights that the student could be.
::不,第二种情况并非如此,例如,如果学生年满18岁,该学生可能身高几高。

The first situation is an example of a function , and the second example is not a function.
::第一种情况是函数的一个例子,第二种情况不是函数。

A function is a relationship where each input number corresponds to one and only one output number.

In the first situation, for each different number of candy bar sales you input , there is one and only one output number representing your profit.
::第一种情况是,你输入的糖果棒销售量各有不同, 只有一个输出数代表你的利润。

In the second situation, if you input "18 years", there are multiple outputs , so you can't identify a specific relationship between age and height.
::在第二种情况下,如果你输入“18岁”, 就会有多重输出, 所以您无法确定年龄和身高之间的特定关系。

See the difference ?
::看到区别了吗?

It is important to note that both situations above are relations. A relation is simply a relationship between two sets of numbers or data. For example, in the second situation, we created a relationship between students’ ages and heights, just by writing each student’s information as an ordered pair . In the first situation, there is a relationship between the number of candy bars you sell and the amount of money you make. The first example is different from the second because it represents a function : every $\begin{aligned} x \end{aligned}$ is paired with only one $\begin{aligned} y \end{aligned}$ .
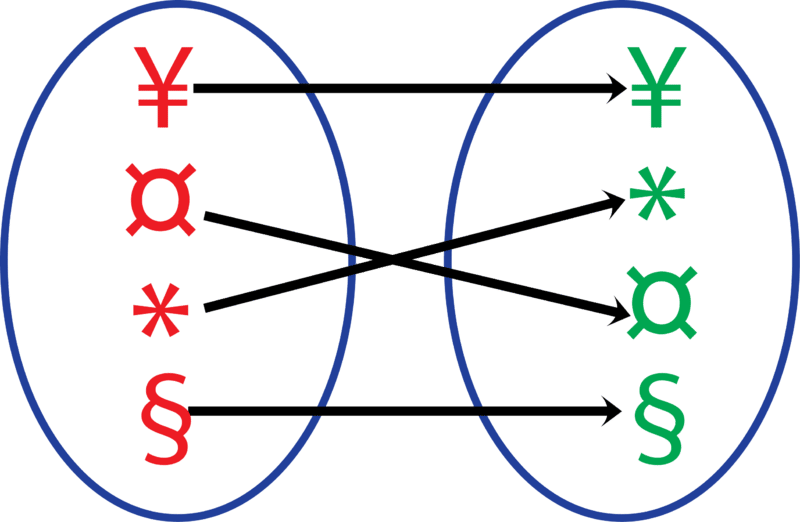
::必须指出,上述两种情况都是关系。一种关系仅仅是两组数字或数据之间的关系。比如,在第二种情况下,我们在学生的年龄和身高之间建立了关系,只是将每个学生的信息写成一对。在第二种情况下,你卖的糖果条数和你赚的钱数额之间存在关系。第一个例子与第二个不同,因为它代表了一个函数:每个x只配一对。

Functions may be presented in many ways. Some of the most common ways to represent functions include: sets of ordered pairs, equations, and graphs. The figure below shows the same function depicted in three different ways.
::函数可以以多种方式显示。一些最常见的函数表达方式包括:一对一对一对一对一对一对一对一对一对一对一对一对一对一对一对一对一对一对一对一对一方方程式和图表。下图显示了以三种不同方式描述的相同功能。

Examples
::实例

Example 1
::例1

Earlier, you were given a question about movie tickets.
::早些时候,你被问到有关电影票的问题。

Does the data you received from your friends represent a function? Can you use the data to predict the cost of going to a movie yourself?
::你从朋友那里得到的数据是否代表一个功能?你能用这些数据来预测自己去看电影的成本吗?

If we were to organize the information we received into ordered pairs, it might look something like: $\begin{aligned} (1, 14.5), (1, 8.75), (1, 5), (1, 17.5), (1, 12.75) \end{aligned}$ where each $\begin{aligned} x \end{aligned}$ value represents the number of tickets bought, and each $\begin{aligned} y \end{aligned}$ value represents the price.
::如果我们将我们收到的信息编成有定购的一对,它可能看起来像:1,14.5,(1,8.75,1,8.75,(1,5,1,17.5),(1,12.75),每x值代表购票数,每y值代表价格。

Since there are many different $\begin{aligned} y \end{aligned}$ values for the only $\begin{aligned} x \end{aligned}$ value, it is definitely not a function.
::由于唯一的 x 值有许多不同的 y 值, 它绝对不是一个函数。

It should be clear now that the information received from friends' text messages cannot really be used to accurately predict the cost of a movie.
::现在应该清楚的是,从朋友的短信中获得的信息实际上不能用来准确预测电影的成本。

Example 2
::例2

Determine if each relation is a function.
::确定每一关系是否是一个函数。

Representation	Example
Set of ordered pairs	(1,3), (2,6), (3,9), (4,12) (a subset of the ordered pairs for this function)
Equation	$\begin{aligned} y = 3 x \end{aligned}$
Graph

In the first representation above, we are given a set of ordered pairs. To verify that this is a function, we must ensure that each $\begin{aligned} x \end{aligned}$ -value is associated with a single $\begin{aligned} y \end{aligned}$ -value. In this example, the first number in each pair (the $\begin{aligned} x \end{aligned}$ -value) is different, so we can be certain that there are no cases where a particular $\begin{aligned} x \end{aligned}$ is associated with more than one $\begin{aligned} y \end{aligned}$ .
::在以上第一个表达式中,我们得到了一组有顺序的配对。为了验证这是一个函数, 我们必须确保每个 x 值与一个 Y 值相关联。在此示例中, 每对的首个数( x 值) 不同, 因此我们可以确定没有特定 x 与一个 y 以上相关连的情况。

In the second representation, the equation of a line, it is apparent that any number put in place of $\begin{aligned} x \end{aligned}$ will result in a different $\begin{aligned} y \end{aligned}$ , since the $\begin{aligned} x \end{aligned}$ number is simply being multiplied by $\begin{aligned} 3 \end{aligned}$ .
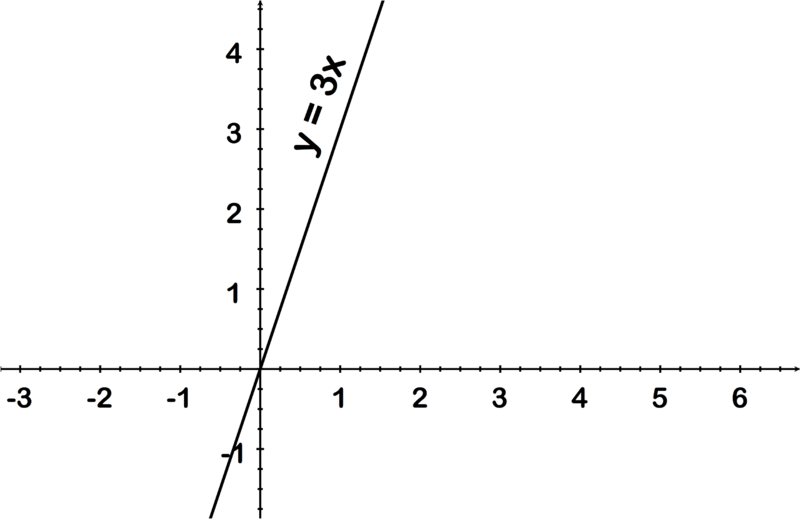
::在第二个表示式,即线的等式中,很明显,以任何数字取代x将产生不同的y,因为x数字只是乘以3。

The third representation above is a graph. A good way to determine whether a relation is a function when looking at a graph is by doing a " vertical line test". If a vertical line can be drawn anywhere on the graph such that the line crosses the relation in two places, then the relation is not a function. If all possible vertical lines will only cross the relation in one place, then the relation is a function. This works because if a vertical line crosses a relation in more than one place it means that there must be two y values corresponding to one x value in that relation. For example, the graph above of $\begin{aligned} y = 3 x \end{aligned}$ shows it is a function because any vertical line that is drawn only crosses the relation in one place.
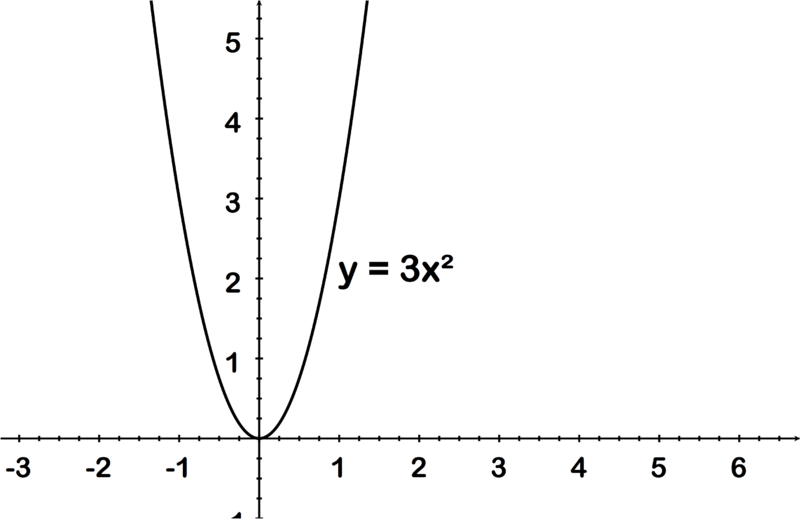
::上面的第三个表示式是一个图形。在查看一个图形时,确定一个关系是否是一个函数的一个很好的方法就是进行“垂直线测试”。如果在图形的任何地方可以绘制一条垂直线,使线横跨两个位置的关系,那么关系不是一个函数。如果所有可能的垂直线只跨越一个地方的关系,那么关系就是一个函数。这是因为,如果垂直线跨不止一个地方的关系,那么如果垂直线跨过一个以上的地点,它意味着在该关系中必须有两个与一个 x 值相对应的y 值。例如,上面的 y=3x 的图表显示这是一个函数,因为所绘制的任何垂直线只跨越一个地方的关系。

Conversely, the graph below of $\begin{aligned} x \end{aligned}$ = $\begin{aligned} y \end{aligned}$ ² shows it is not a function because a vertical line can be drawn that crosses the relation in two places.
::反之, x = y2 下方的图表显示它不是一个函数,因为可以绘制垂直线,横跨两个地方的关系。

Example 3
::例3

Determine if each relation is a function.
::确定每一关系是否是一个函数。

(2, 4), (3, 9), (5, 11), (5, 12)

This relation is not a function because 5 is paired with 11 and with 12.
::这种关系不是一个功能,因为5与11和12对齐。

Function defined as:
::函数定义如下:

::函数定义如下:

This relation is a function because every $\begin{aligned} x \end{aligned}$ is paired with only one $\begin{aligned} y \end{aligned}$ . A vertical line through the graph will always only encounter a single point.
::此关系是一个函数, 因为每个 x 仅配上一个 Y。通过图形的垂直线将总是只遇到一个点。

Example 4
::例4

Determine if the following relation is a function: $\begin{aligned} (- 1, 4), (0, 3), (1, 5), (1, 7), (2, 15) \end{aligned}$ .
::确定以下关系是否是一个功能-1,4,(0,3,),(1,5,1,5,7,(2,15))。

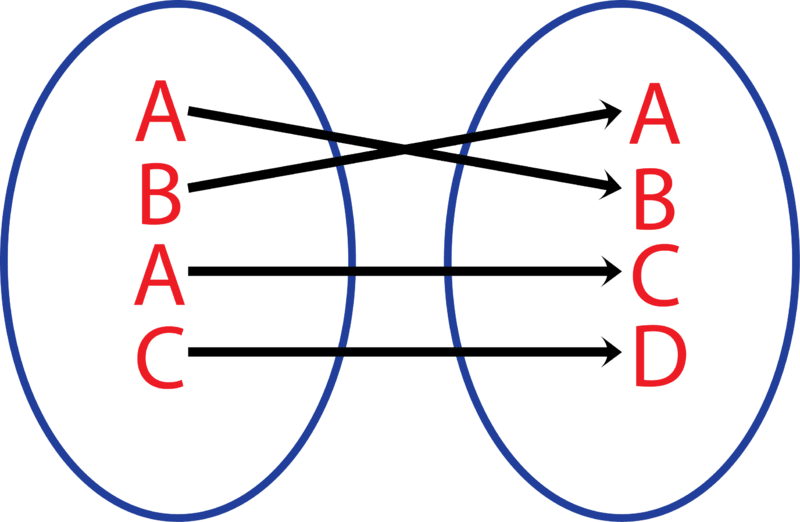
There are two different 'outputs' or $\begin{aligned} y \end{aligned}$ -values for the 'input' or $\begin{aligned} x \end{aligned}$ -value of 1. Because we cannot know whether 1 should go with 5 or 7 at any given time, this relation is not a function.
::1 1 的“ 输入” 折数值有两个不同的“ 输出” 或值, 因为我们不知道1 在任何特定时间是否应该与 5 或 7 相配, 这种关系是 Isota 函数。

Example 5
::例5

Determine if the following relation is a function: $\begin{aligned} y = 4 x \end{aligned}$ .
::确定以下关系是否是一个函数:y=4x。

This is a function. Any value chosen for x has one and only one associated value for y (4 times as big).
::这是一个函数。为 x 所选择的任何值只有 y 的 1 和 1 个相关值( 4 倍于大 ) 。

Review
::回顾

What is the definition of a function?
::函数的定义是什么?

Can a function definition be written in the form $\begin{aligned} x = 3 y \end{aligned}$ instead of $\begin{aligned} y = 3 x \end{aligned}$ ?
::函数定义能否以 x=3y 而不是 y=3x 的形式写入 ?

Is it mandatory for a function to have both an input and an output?
::一项函数必须同时有输入和输出吗?

Can a statement be a function if there is only one input and output?
::如果只有一个输入和输出, 语句能否成为函数 ?

Give an example of a relation that is not a function, and explain why it is not a function.
::请举一个非函数关系的例子,并解释为什么它不是函数。

For questions 6 - 14, identify each relation as either a function, or not a function:
::关于问题6-14,将每一关系确定为一项职能或一项职能,或非一项职能:

(2, 4) (4, 6) (6, 8) (3, 4) (5, 7) (8, 2)
(-1, 6) (0, 4) (-4, 0) (-1, -6) (-3, -8)

(Jim, Kitty) (Joe, Betty) (Brian, Alice) (Jesus, Anissa) (Ken, Kelli)
:吉姆,凯蒂) (乔,贝蒂) (布里安,爱丽丝) (耶稣,阿尼萨) (肯,凯利)

(Jim, Alice) (Joe, Alice) (Brian, Betty) (Jim, Kitty) (Ken, Anissa)
:吉姆,爱丽丝) (乔,爱丽丝) (布里安,贝蒂) (吉姆,凯蒂) (肯,阿尼萨)

At a Prom dance, each boy pins a corsage on his date. Is this an example of a function?
::在一次舞会上,每个男孩都在他的约会上插上皮带。这是功能的一个例子吗?

Later, at the same dance, Cory shows up with two dates, does this change the answer?
::后来,在同一场舞蹈中,科里带着两个日期出现,这是否改变了答案?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

关系和职能

Relations and Functions ::关系和职能

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)