1.5 最低和最高

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 最低和最高限数

  Collapse Expand

  最低和最高限数

  播放段落

  You run a business drawing caricatures. You currently have 25 drawings of rap artists and 25 drawings of "Glee" actors and actresses to sell. You can continue to draw 5 pictures per day if you are not taking the time to sell what you have already. Unfortunately, one of your classmates has seen what a great business this is, and plans to start selling pictures herself. Right now you sell each caricature for $20, but you know when your friend starts to compete for sales, you will have to discount your price to stay competitive. Assuming your sales price goes down by $1 per day, how long should you continue to draw caricatures before selling, so you make the maximum profit?
  ::您正在经营一个商业漫画。 您目前有25幅饶舌歌手画和25幅“ 欢乐” 演员和女演员的画要出售。 如果您没有花时间卖掉你已有的, 您可以继续每天画5幅图片。 不幸的是, 您的同学之一已经看到这幅画是一件多么伟大的生意, 并计划自己开始出售图片。 现在您将每幅漫画都卖20美元, 但是您知道当您的朋友开始竞争销售时, 您需要贴现价格才能保持竞争力。 假设您的销售价格每天降低1美元, 您在销售前还要继续画漫画多久, 所以您才能获得最大的利润 ?

  播放段落

  Minimums and Maximums
  ::最低和最高限数

  播放段落

  In real life, it is common to need to identify what combinations of values result in a maximum or minimum quantity, collectively called extrema . It is important to note that not all functions have extrema.
  ::在现实生活中,通常需要确定什么是价值组合导致最大或最低数量,统称为extrema,必须指出,并非所有功能都有极限。

  播放段落

  Minimums
  ::最低

  播放段落

  Formally: The point ( c, f ( c )) is the minimum value of a function if f ( c ) ≤ f ( a ) for all elements a ( a ≠ c ) of the domain of f .
  ::正式规定:如果f(c)-f(a)适用于f领域(a)-(c)的所有要素,则(c)点(f)(c)是函数的最小值。

  播放段落

  Informally: The point ( c, f ( c )) is the minimum if all other function values are greater than or equal to f ( c ).
  ::非正式方式:如果所有其他函数值大于或等于f(c),则(c),f(c)点为最低值。

  播放段落

  Maximums
  ::最大

  播放段落

  Formally: The point ( c , f ( c )) is the maximum of f ( x ) if f ( c ) ≥ f ( a ) for all elements a ( a ≠ c ) of the domain of f .
  ::正式规定:如果f(c)-f(a)对于f领域的所有要素a(a)-(c),(c)点(f)(c)是f(x)的上限。

  播放段落

  Informally: The point ( c , f ( c )) is the maximum if all other function values are less than or equal to f ( c ).
  ::非正式方式:如果所有其他函数值小于或等于f(c),(c),(f(c))点为最大值。

  播放段落

  Examples 
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were given a problem about the caricature business.
  ::早些时候,你被问及 漫画业的问题。

  播放段落

  You currently have 25 drawings of rap artists and 25 drawings of "Glee" actors and actresses to sell. You can continue to draw 5 pictures per day if you are not taking the time to sell what you have already. Unfortunately, one of your classmates has seen what a great business this is, and plans to start selling pictures herself. Right now you sell each caricature for $20, but you know when your friend starts to compete for sales, you will have to discount your price to stay competitive. Assuming your sales price goes down by $1 per day, how long should you continue to draw caricatures before selling, so you make the maximum profit?
  ::您目前拥有25幅饶舌歌手的绘画和25幅“欢乐”演员和女演员的绘画供销。 如果您没有花时间出售已经拥有的作品,您可以继续每天画5幅图片。 不幸的是,您的一位同学已经看到了这多么伟大的生意,并计划自己开始出售图片。 现在,您将每一幅漫画卖出20美元,但您知道当你的朋友开始竞争销售时,您必须贴现价格才能保持竞争力。假设您的销售价格每天下跌1美元,那么您在销售前还要画多久的漫画,才能获得最大的利润?

  播放段落

  First describe the number of pictures available for sale based on the number of days, starting with the original 50 and increasing by 5 per day: $\begin{array}{r}(50+5d)\end{array}$ .
  ::首先说明可出售的照片数量,以天数为基础,从原来的50天开始,每天增加5张50+5d)。

  播放段落

  Next set the sales price as a function of the number of days, starting at the original price of $20, decreasing by $1 per day: $\begin{array}{r}(20-1d)\end{array}$ .
  ::接下来将销售价格设定为天数的函数,从最初价格20美元起算,每天减少1美元20-1d)。

  播放段落

  Now multiplying the two expressions together represents the income from the number of pictures available at the current price, based on the number of days from start: $\begin{array}{r}(50+5d)(20-d)\end{array}$
  ::现在将两个表达式合并乘以, 表示以当前价格提供的图片数的收入, 以起始天数为基础 50+5d)( 20- d)

  播放段落

  Set the combined function equal to zero and solve for the intercepts: $\begin{array}{r}(50+5d)(20-d)=0\end{array}$ . This yields the zeroes of -10 and 20. Since the expression describes a parabola , midway between the x coordinates of -10 and 20 would be the vertex, representing the greatest value resulting from the combination of sales price and number of pictures: +5
  ::设定拦截的合并函数为零, 并解决 : (50+5d)(20- d)=0。 得出零为 -10 和 20 。 由于表达式描述的是一个抛物线, x 坐标 - 10 和 20 之间的中间线将是顶点, 代表销售价格和图片数相结合的最大值 :+5

  播放段落

  The greatest profit results from selling the pictures 5 days after the start.
  ::最大的利润来自于 开始5天后卖掉这些照片

  播放段落

  If you are curious what the profit would be, or how many pictures would be sold, simply replace the variable (d) with the calculated value of 5. The value of the first expression: $\begin{array}{r}[(50-5(5)]\end{array}$ represents the number of pictures 5 days along. The value of the second expression $\begin{array}{r}[20-1(5)]\end{array}$ represents the sales price per picture on day 5. The value of the complete expression: $\begin{array}{r}[50-5(5)][20-1(5)]\end{array}$ represents total income.
  ::如果您想知道利润是多少,或者要出售多少幅图片,只需将变量(d)改为计算值为5。第一个表达式的值:[(50-5(5))]代表相隔5天的图片数。第二个表达式的值[20-1(5)]代表第5天每张照片的销售价格。完整表达式的值:[50-5(5)][20-1(5)]代表总收入。

  播放段落

  Example 2
  ::例2

  播放段落

  Determine if each function has a minimum or a maximum point.
  ::确定每个函数是否有最低点或最高点。

  播放段落
  1. y = 2 x - 1
     ::y = 2x-1

  播放段落

  The graph of y = 2 x - 1 is a line. It does not have a maximum or a minimum.
  ::y = 2x - 1 的图形是一个线条。它没有最大值或最小值。

  播放段落
  2. y =  x ⁴
     ::y = x4 y = x4

  播放段落

  The graph of y = x ⁴ has a minimum value at (0,0). It does not have a maximum.
  ::y = x4 的图形的最小值为 0,0。它没有最大值。

  播放段落

  Example 3
  ::例3

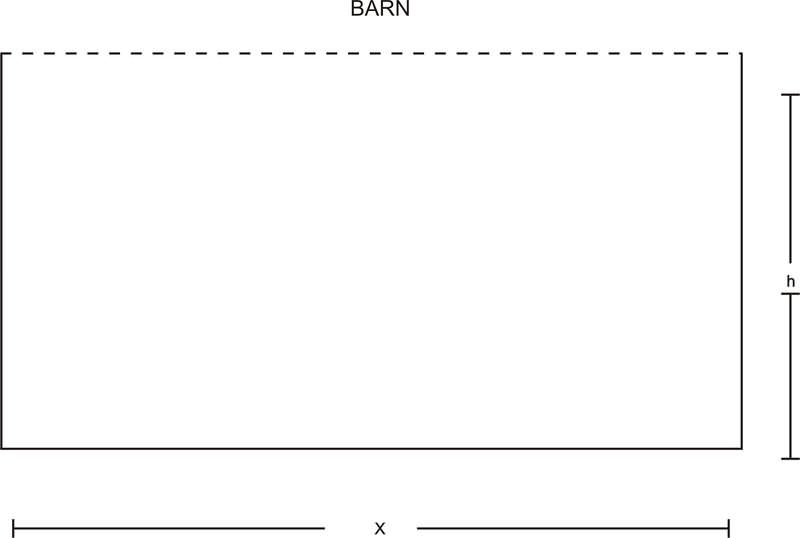
  播放段落

  You have 100 feet of fence with which to enclose a plot of land on the side of a barn. You want the enclosed land to be a rectangle. What size rectangle should you make with the fence in order to maximize the area of the rectangular enclosure?
  ::您有100英尺长的栅栏, 可以在谷仓的边上盖上一块土地。 您希望封闭的土地是一个矩形。 您应该用栅栏做多大的矩形, 以便尽可能扩大长方形封闭区面积 ?

  播放段落

  The plot of land will look like the picture below:
  ::地块将看起来像下面的图景:

  

  播放段落

  The area of the rectangular plot is the product of its length and width. We can write the area as a function of x: A ( x ) = xh . We can eliminate h from the equation if we consider that we have 100 feet of fence, and we write an equation about how we are using that 100 feet of fence: x + 2 h = 100. (The fourth side of the rectangle does not require fence because of the barn.) We can solve this equation for h and substitute into the area equation:
  ::矩形图的面积是其长度和宽度的产物。 我们可以将区域写成 x 的函数 : A(x) = xh。 如果我们考虑到我们有100英尺的栅栏, 我们可以从方程式中删除 h。 我们写一个方程式,说明我们如何使用这100英尺的栅栏: x + 2h = 100. (矩形的第四面由于谷仓而不需要栅栏 。) 我们可以解决这个方程式 h, 并替换成区域方程式 :

  $$\begin{array}{rl}& x+2h=100\\ \Rightarrow & 2h=100-x\\ \Rightarrow & h=50-\frac{x}{2}\end{array}$$

  播放段落

  $$\begin{array}{rl}A(x)& =xh\\ & =x\left(50-\frac{x}{2}\right)\\ & =50x-\frac{x^2}{2}\end{array}$$

  
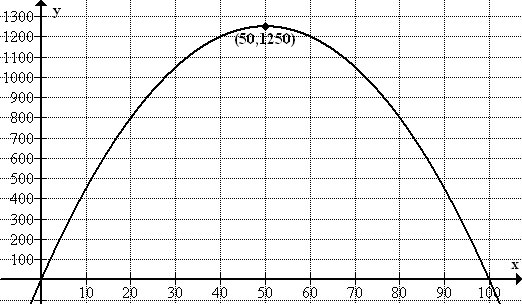
  ::A(x)=xh=x(50-x2)=50x-x22

  播放段落

  The graph of A ( x ) is shown here on the interval [0,100]. Using a maximum function on a graphing utility tells us that the point (50,1250) is the maximum point. This tells us that when the rectangle’s width is 50 ft, the area is 1250 ft ² .
  ::A(x) 的图形显示在间隔 [0,100] 上。使用图形工具的最大函数告诉我们, 点( 50, 1250) 是最大点。 这告诉我们, 当矩形的宽度为 50 英尺时, 区域是 1,250 英尺 2 。

  

  播放段落

  Example 4
  ::例4

  播放段落

  What is the minimum possible surface area of a box with a square base and a fixed volume of 12 cm ³ ?
  ::一个有方基和固定体积为12厘米3的盒子的最小可能表面面积是多少?

   

  播放段落

  Let the length and the width of the box be x cm, and the height be h cm. We can write the volume equation as $\begin{array}{r}x\cdot x\cdot h=x^{2}h=12\end{array}$ . We can also express the surface area in terms of x and h :
  ::让框的长度和宽度为 x cm, 高度为 h cm 。 我们可以将音量方程式写成 x xx\h=x2h=12。 我们也可以以 x 和 h 表示表面积 :

  $\begin{array}{r}\text{Surface area}=S=4xh+2x^2\end{array}$

  播放段落

  (The base and the top are squares with area = $\begin{array}{r}{x}^2\end{array}$ and the four sides are each rectangles of area equal to $\begin{array}{r}xh\end{array}$ ).
  :底部和顶部是面积=x2的方形,四边是面积等于xh的方形)。

  播放段落

  We can express the surface area as a function of x if we consider the volume equation and the surface area equation as a system of equations:
  ::如果我们将体积方程式和表面积方程式作为方程式系统来考虑,我们可以以x的函数表示表面积:

  $$\begin{array}{r}\{\begin{array}{l}{x}^{2}h=12\\ 4xh+2x^2=S\end{array}\end{array}$$

  播放段落

  We want to work with the surface area equation since that is what we want to minimize. It will be easier to graph and analyze surface area if we can express S in terms of just one other variable. Rewrite the surface area equation as a function of x :
  ::我们希望与表面积方程式合作, 因为这是我们想要最小化的。 如果我们能用其它一个变量来表示 S , 图表和分析表面积比较容易。 重写表面积方程式, 以 x 函数 :

  播放段落

  First, rewrite the volume equation:
  ::首先,重写音量方程:

  播放段落

  $\begin{array}{r}{x}^{2}h=12\Rightarrow h=\frac{12}{x^2}\end{array}$
  ::x2h=12\\h=12x2

  播放段落

  Now, use substitution:
  ::现在,使用替代:

  播放段落

  $$\begin{array}{rl}S(x)& =4xh+2x^2\\ & =4x\left(\frac{12}{x^2}\right)+2x^2\\ & =\frac{48}{x}+2x^2\end{array}$$

  
  ::S(x)=4xh+2x2=4x(12x2)+2x2=48x+2x2

  播放段落

  The values of the function S ( x ) represent different possibilities for the surface area of the box, given that the base is a square, and given that the volume of the box is 12 cm ³ . To identify the minimum surface area, we need to find the lowest function values for S ( x ).
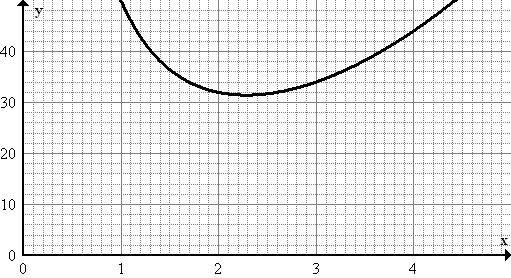
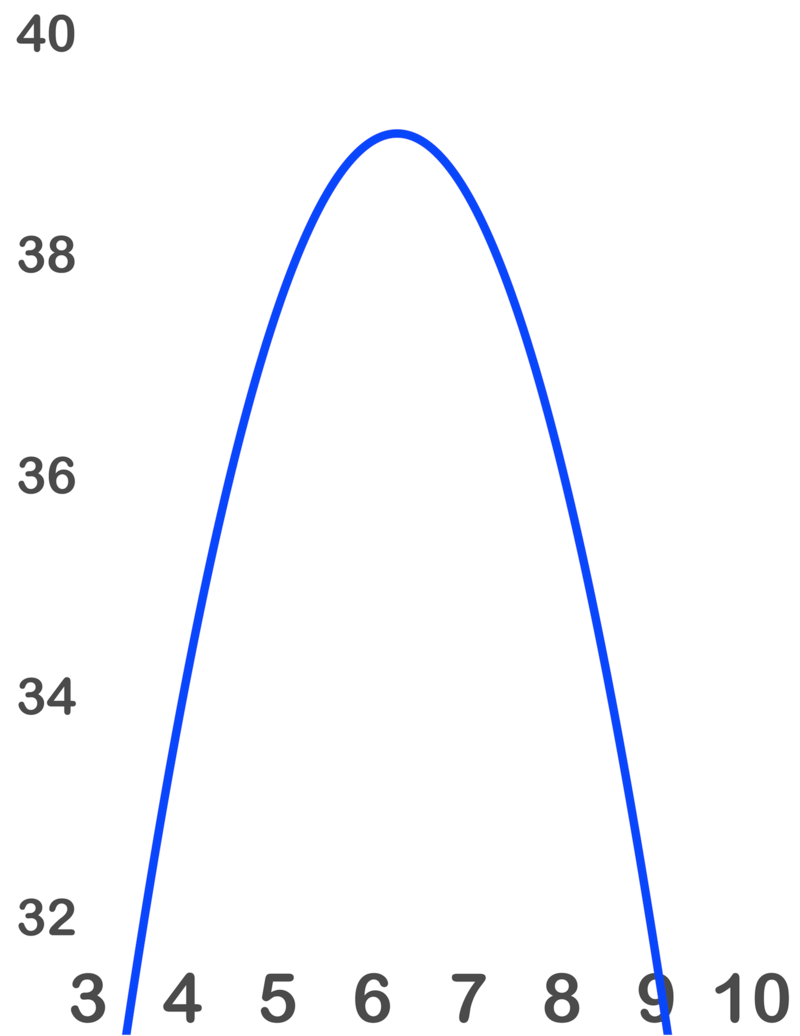
  ::函数S(x) 的值代表框表面区域的不同可能性,因为基数是一个平方,并且鉴于框的体积是12厘米3。 为了确定最小表面区域,我们需要找到S(x) 的最低函数值。

  播放段落

  The graph below shows the function S ( x ) on the interval [0,5]. By examining the graph, we can see that the lowest point is between x = 2 and x = 3. If you use a “minimum” function on a graphing utility, you will find that the minimum point is approximately (2.3, 31.4). This tells us that when the side length of the box is approximately 2.3 cm, the surface area is approximately 31.4 cm ² , which is the smallest it can be.
  ::下图显示间距[0,5] 的函数 S(x) 。通过检查图形,我们可以看到最低点在 x = 2 和 x = 3. 之间。如果在图形工具上使用“最小”函数,你会发现最小点大约(2.3,31.4)。这告诉我们,当框的侧长大约2.3厘米时,表面面积约为31.4厘米,这是最小的。

  

  播放段落

  Example 5
  ::例5

  播放段落

  A rectangle has a perimeter of 25in. Write an expression for the area of the rectangle as a function of its width ’’x’’ and graph this expression.
  ::矩形的周边为 25 英寸。 将矩形区域的表达式写成它的宽度 x 函数, 并绘制此表达式的图示 。

  播放段落

  The area of a rectangle is $\begin{array}{r}l\cdot w\end{array}$
  ::矩形区域为 lw

  播放段落

  The perimeter is $\begin{array}{r}2\cdot l+2\cdot w\end{array}$
  ::周边是2l+2w

  播放段落

  Therefore we have: $\begin{array}{r}25=2(l+w)\end{array}$
  ::因此,我们有:25=2(l+w)

  播放段落

  $\begin{array}{r}12.5=l+w\end{array}$
  ::12.5=l+w

  播放段落

  $\begin{array}{r}12.5-w=l\end{array}$
  ::12.5-w=l

  播放段落

  $\begin{array}{r}A=x(12.5-x)\end{array}$
  ::Ax = (12.5-x)

  播放段落

  Using a graphing tool, like  , we have:
  ::使用图表工具,例如,我们有:

  

  播放段落

  Review
  ::回顾

  播放段落
  1. What quantity should be maximized? What quantity should be minimized? You are manufacturing chairs, and it costs you a certain amount of money to make each chair. You need to determine the selling price of the chairs.
     ::最大数量应该达到什么数量? 最小数量应该达到什么数量? 你们是制造椅子的,每张椅子要花一定的钱。你们需要决定椅子的销售价格。
  播放段落
  2. A rectangle has area 20 in ² . Write an expression for the perimeter of the rectangle as a function of its width x .
     ::矩形区域 20 英寸 2 。 矩形周围的表达式, 根据其宽度 x 的函数, 写入矩形周围的表达式 。
  播放段落
  3. What dimensions of the rectangle in problem #2 will minimize its perimeter? What is the minimum perimeter? (These values will be approximations.)
     ::问题2的矩形的什么维度能将周界最小化?最小周界是多少? (这些值将是近似值。 )
  播放段落
  4. In your own words, define the term “maximum of a function.”
     ::用你自己的话来说,定义“一项职能的最大”一词。
  播放段落
  5. Explain how you can use a graph to identify global extrema of a function.
     ::解释您如何使用图表来识别函数的全局矩形。
  播放段落
  6. A rectangle has a perimeter of 24 inches. What is the maximum area the rectangle can have?
     ::矩形的周长为24英寸。矩形的最大区域是多少?
  播放段落
  7. A cylindrical canister has a volume of 30 in ³ . What is the radius of the canister with minimum surface area? (Volume of a cylinder is $\begin{array}{r}V=\pi r^{2}h\end{array}$
     ::圆柱体罐体的体积为30英寸3. 罐体的半径与最小表面面积是多少? (圆柱体的体积是Vr2h)
  播放段落
  8. Consider the function f ( x ) = bx ² + 7. For what values of b will the function have a maximum?
     ::考虑函数 f( x) = bx2 + 7 。 对于 b 的值, 该函数的最大值是多少 ?
  播放段落
  9. Consider the function $\begin{array}{r}S(x)=\frac{48}{x}+2x^2\end{array}$ . How can you tell that this function does not have a global maximum or minimum?
     ::考虑 S( x) = 48x+2x2 函数。 您如何判断此函数没有全球最大值或最小值 ?
  播放段落
  10. A rectangle has perimeter P . Write a function for the area of the rectangle as a function of P and x , the width of the rectangle. What do you think will be the rectangle with maximum area?
      ::矩形 矩形 有 周边 P 。 写入矩形 区域 的 函数, 作为 P 和 x 的函数, 矩形 的宽度 。 您认为最大 区域 的 矩形 会是什么 ?
  播放段落
  11. A rectangular lot beside a river is fenced on the other 3 sides with 80ft of fencing. What is the largest possible size of the lot?
      ::一条河旁的长方形建筑在另外三边围有80英尺的栅栏。

  播放段落

  Problems 12 - 15: Determine whether each function has a maximum or minimum.
  ::问题12-15:确定每项职能的上限或最低限值。

  播放段落
  12. $\begin{array}{r}y=x^2\end{array}$
      ::y=x2 y=x2
  播放段落
  13. $\begin{array}{r}y=x^3\end{array}$
      ::y=x3 y=x3
  播放段落
  14. $\begin{array}{r}y=|x|\end{array}$
      ::~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
  播放段落
  15. $\begin{array}{r}y=x+3\end{array}$
      ::y=x+3 y=x+3

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。