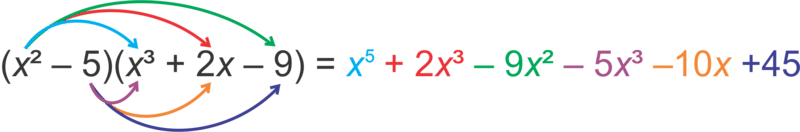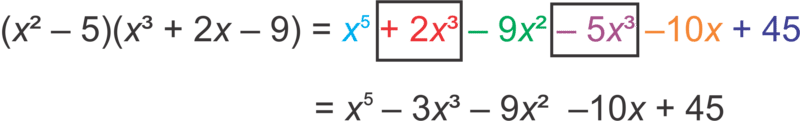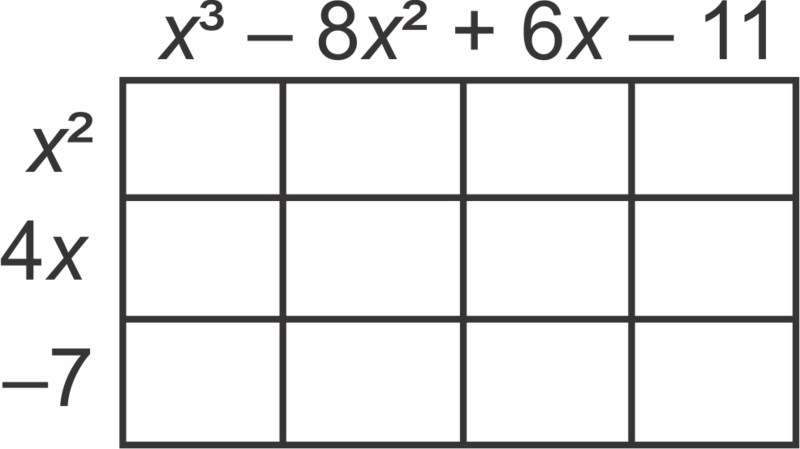Course: 6.5 乘以多边多边体

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 乘以多边多边形

Collapse Expand
乘以多边多边形
The length of a rectangular garden plot is $\begin{aligned} x^{3} + 5 x^{2} - 1 \end{aligned}$ . The width of the plot is $\begin{aligned} x^{2} + 3 \end{aligned}$ . What is the area of the garden plot?
::矩形花园地块的长度为 x3+5x2-1。地块的宽度为 x2+3 。花园地块的面积是多少?

Multiplying Polynomials
::乘以多边多边形

Multiplying together is very similar to multiplying together factors. You can FOIL or we will also present an alternative method. When multiplying together polynomials, you will need to use the properties of exponents, primarily the Product Property $\begin{aligned} (a^{m} \cdot a^{n} = a^{m + n}) \end{aligned}$ and combine like terms .
::乘在一起与乘在一起非常相似。您可以使用FIL 或我们提供一种替代方法。当将多面体乘在一起时, 您需要使用指数属性, 主要是产品属性( aman= am+n) , 并结合类似条件。

Find the following product.
::找到以下产品。

$\begin{aligned} (x^{2} - 5) (x^{3} + 2 x - 9) \end{aligned}$

:x2-5(x3+2x-9))

Using the FOIL method, you need be careful. First, take the $\begin{aligned} x^{2} \end{aligned}$ in the first polynomial and multiply it by every term in the second polynomial.
::使用 FIL 方法, 您需要小心。首先, 在第一个多数值组中取 x2 乘以第二个多数值组中的每个术语。

Now, multiply the -5 and multiply it by every term in the second polynomial.
::现在,乘以 - 5 乘以它乘以第二个多种族体的每个术语。

Lastly, combine any like terms. In this example, only the $\begin{aligned} x^{3} \end{aligned}$ terms can be combined.
::最后,将任何类似术语结合起来,在这个例子中,只有 x3 术语可以合并。

Find the following product.
::找到以下产品。

$\begin{aligned} (x^{2} + 4 x - 7) (x^{3} - 8 x^{2} + 6 x - 11) \end{aligned}$

:x2+4x-7(x3-8x2+6x-11)

In this problem , we will use the “box” method. Align the two polynomials along the top and left side of a rectangle and make a row or column for each term. Write the polynomial with more terms along the top of the rectangle.
::在此问题上, 我们将使用“ 框” 方法。在矩形的顶部和左侧对齐两个多边形对齐, 并为每个术语绘制一行或一列。在矩形的顶部写一行或一列。在矩形的顶部用更多词写一行或一列。

Multiply each term together and fill in the corresponding spot.
::将每个学期乘以一个学期并填充相应的学分。

Finally, combine like terms. The final answer is $\begin{aligned} x^{5} - 4 x^{4} - 33 x^{3} + 69 x^{2} - 86 x + 77 \end{aligned}$ . This method presents an alternative way to organize the terms. Use whichever method you are more comfortable with. Keep in mind, no matter which method you use, you will multiply every term in the first polynomial by every term in the second.
::最后,将类似术语合并。最后一个答案是 x5- 4x4- 33x3+69x2- 86x+77。此方法为术语组织提供了另一种方法。使用您比较舒适的方法。记住, 无论您使用哪种方法, 您都会在第一个多义中将每个术语乘以第二个术语中的每个术语。

Find the following product.
::找到以下产品。

$\begin{aligned} (x - 5) (2 x + 3) (x^{2} + 4) \end{aligned}$

:x-5)(2x+3)(x2+4)

In this problem we have three binomials. When multiplying three polynomials, start by multiplying the first two binomials together.
::在这个问题上,我们有三个二进制。在乘以三个多元体时,首先将前两个二进制相乘。

$\begin{aligned} (x - 5) (2 x + 3) & = 2 x^{2} + 3 x - 10 x - 15 \\ = 2 x^{2} - 7 x - 15 \end{aligned}$

:x-5)(2x+3)=2x2+3x-10x-10x-15=2x2-7x-15)

Now, multiply the answer by the last binomial .
::现在,将答案乘以最后一个二元论。

$\begin{aligned} (2 x^{2} - 7 x - 15) (x^{2} + 4) & = 2 x^{4} + 8 x^{2} - 7 x^{3} - 28 x - 15 x^{2} - 60 \\ = 2 x^{4} - 7 x^{3} - 7 x^{2} - 28 x - 60 \end{aligned}$

:2x2-7x-15)(x2+4)=2x4+8x2-7x3-28x-15x2-60=2x4-7x3-7x2-28x-60)

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the area of the garden plot.
::早些时候,有人要求你找到园地的面积。

Recall that the area of a rectangle is $\begin{aligned} A = l w \end{aligned}$ , where l is the length and w is the width. Therefore , we need to multiply.
::回顾矩形的区域是 A=lw, 其中我为长度和宽度。因此, 我们需要乘以。

$\begin{aligned} A = (x^{3} + 5 x^{2} - 1) (x^{2} + 3) \\ = x^{5} + 3 x^{3} + 5 x^{4} + 15 x^{2} - x^{2} - 3 \end{aligned}$

::A=(x3+5x2-2-1)(x2+3)=x5+3x3+5x4+15x2-x2-3)

Now combine like terms and simplify. Be sure to write your answer in standard form
::现在将类似条件和简化合并。请务必以标准格式写入您的回答

$\begin{aligned} x^{5} + 3 x^{3} + 5 x^{4} + (15 x^{2} - x^{2}) - 3 \\ = x^{5} + 3 x^{3} + 5 x^{4} + 14 x^{2} - 3 \\ = x^{5} + 5 x^{4} + 3 x^{3} + 14 x^{2} - 3 \end{aligned}$

::x5+3x3+5x4+(15x2-x2)-3=5+3x3+5x3+5x4+14x2=3x5+5x4+5x4+3x3+3x3+14x2_3

Therefore, the area of the garden plot is $\begin{aligned} x^{5} + 5 x^{4} + 3 x^{3} + 14 x^{2} - 3 \end{aligned}$ .
::因此,花园地块面积为 x5+5x4+3x3+14x2-3。

Example 2
::例2

Find the product: $\begin{aligned} - 2 x^{2} (3 x^{3} - 4 x^{2} + 12 x - 9) \end{aligned}$ .
::查找产品:-2x2(3x3-4x2+12x-9)。

Use the to multiply $\begin{aligned} - 2 x^{2} \end{aligned}$ by the polynomial.
::使用多元数乘以 2- 2x2。

$\begin{aligned} - 2 x^{2} (3 x^{3} - 4 x^{2} + 12 x - 9) = - 6 x^{5} + 8 x^{4} - 24 x^{3} + 18 x^{2} \end{aligned}$

::-2x2(3x3)-4x2+12x-9**6x5+8x4-24x3+18x2

Example 3
::例3

Find the product: $\begin{aligned} (4 x^{2} - 6 x + 11) (- 3 x^{3} + x^{2} + 8 x - 10) \end{aligned}$ .
::查找产品4x2-6x+11)(-3x3+x2+8x-10)

Multiply each term in the first polynomial by each one in the second polynomial.
::将第一个多义中的每个术语乘以第二个多义中的每个术语。

$\begin{aligned} (4 x^{2} - 6 x + 11) (- 3 x^{3} + x^{2} + 8 x - 10) & = - 12 x^{5} + 4 x^{4} + 32 x^{3} - 40 x^{2} \\ + 18 x^{4} - 6 x^{3} - 48 x^{2} + 60 x \\ - 33 x^{3} + 11 x^{2} + 88 x - 110 \\ = - 12 x^{5} + 22 x^{4} - 7 x^{3} - 77 x^{2} + 148 x - 110 \end{aligned}$

:- 3x3+x2+x2+8x- 10)\\12x5+4x4+32x3-40x2+18x4 - 6x2 - 6x2 - 6x3 - 482 - 6x3 - 482 - 6x3 - 6x3 - 482 - 660x - 33x3+112+112+112x2+188x - 110=12x5+22x4 - 7x3-33x2+148x-110)

Example 4
::例4

Find the product: $\begin{aligned} (x^{2} - 1) (3 x - 4) (3 x + 4) \end{aligned}$ .
::查找产品x2-1)(3x-4)(3x+4)。

Multiply the first two binomials together.
::将前两个二进制相乘。

$\begin{aligned} (x^{2} - 1) (3 x - 4) = 3 x^{3} - 4 x^{2} - 3 x + 4 \end{aligned}$

:x2-1)(3x-4)=3x3-4x2-3x+4)

Multiply this product by the last binomial.
::用最后一个二进制乘以此产品。

$\begin{aligned} (3 x^{3} - 4 x^{2} - 3 x + 4) (3 x + 4) & = 9 x^{4} + 12 x^{3} - 12 x^{3} - 16 x^{2} - 9 x^{2} - 12 x + 12 x - 16 \\ = 9 x^{4} - 25 x^{2} - 16 \end{aligned}$

:3x4)=9x4+12x3-12x3-12x3-16x2-9x2-12x2-12x2-12x-16x-16=9x4-25x2-16)

Example 5
::例5

Find the product: $\begin{aligned} (2 x - 7)^{2} \end{aligned}$ .
::查找产品2x-7)2。

The square indicates that there are two binomials. Expand this and multiply.
::方形表示有两个二进制。放大和乘以。

$\begin{aligned} (2 x - 7)^{2} & = (2 x - 7) (2 x - 7) \\ = 4 x^{2} - 14 x - 14 x + 49 \\ = 4 x^{2} - 28 x + 49 \end{aligned}$

:2x-7)2=(2x-7)2=(2x-7)(2x-7)=4x2-14x-14x-14x+49=4x2-28x+49

Review
::回顾

Find the product.
::找到产品。

$\begin{aligned} 5 x (x^{2} - 6 x + 8) \end{aligned}$
::5x(x2-6x+8)

$\begin{aligned} - x^{2} (8 x^{3} - 11 x + 20) \end{aligned}$
::-x2(8)x3-11x+20

$\begin{aligned} 7 x^{3} (3 x^{3} - x^{2} + 16 x + 10) \end{aligned}$
::7x3(3x3-x2+16x+10)

$\begin{aligned} (x^{2} + 4) (x - 5) \end{aligned}$
:x2+4)(x-5)

$\begin{aligned} (3 x^{2} - 4) (2 x - 7) \end{aligned}$
:3x2-4(2x-7))

$\begin{aligned} (9 - x^{2}) (x + 2) \end{aligned}$
:9-x2(x+2))

$\begin{aligned} (x^{2} + 1) (x^{2} - 2 x - 1) \end{aligned}$
:x2+1)(x2-2-2x-1)

$\begin{aligned} (5 x - 1) (x^{3} + 8 x - 12) \end{aligned}$
:5x-1(x3+8x-12))

$\begin{aligned} (x^{2} - 6 x - 7) (3 x^{2} - 7 x + 15) \end{aligned}$
:x2-6x-7)(3x2-7x+15)

$\begin{aligned} (x - 1) (2 x - 5) (x + 8) \end{aligned}$
:x-1)(2x-5)(x+8)

$\begin{aligned} (2 x^{2} + 5) (x^{2} - 2) (x + 4) \end{aligned}$
:2x2+5)(x2-2)(x+4)

$\begin{aligned} (5 x - 12)^{2} \end{aligned}$
:5x-12)2

$\begin{aligned} - x^{4} (2 x + 11) (3 x^{2} - 1) \end{aligned}$
::-x4(2xx+11)(3x2-1)

$\begin{aligned} (4 x + 9)^{2} \end{aligned}$
:4x+9)2

$\begin{aligned} (4 x^{3} - x^{2} - 3) (2 x^{2} - x + 6) \end{aligned}$
:4x3 - x2 - 3)(2x2 - x6)

$\begin{aligned} (2 x^{3} - 6 x^{2} + x + 7) (5 x^{2} + 2 x - 4) \end{aligned}$
:2x3-6x2+x7)(5x2+2x-4)

$\begin{aligned} (x^{3} + x^{2} - 4 x + 15) (x^{2} - 5 x - 6) \end{aligned}$
:x3+x2-4x+15)(x2-5x-6)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

乘以多边多边形

Multiplying Polynomials ::乘以多边多边形

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Multiplying Polynomials
::乘以多边多边形

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)