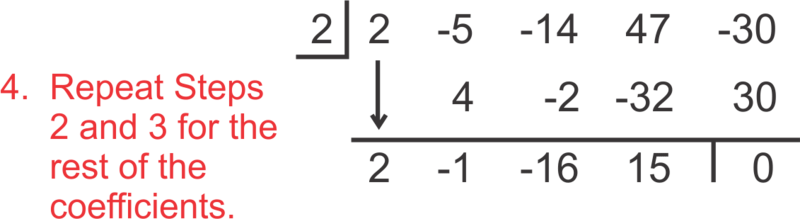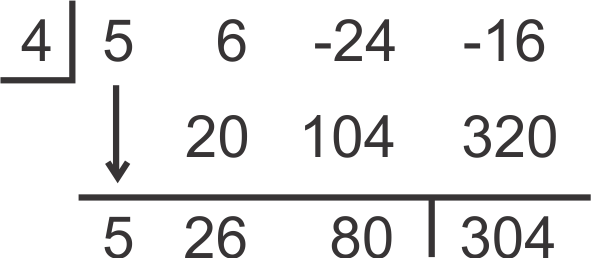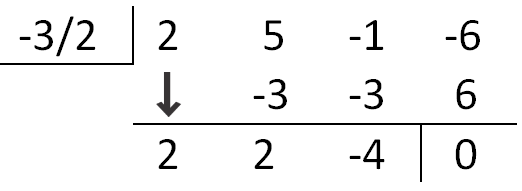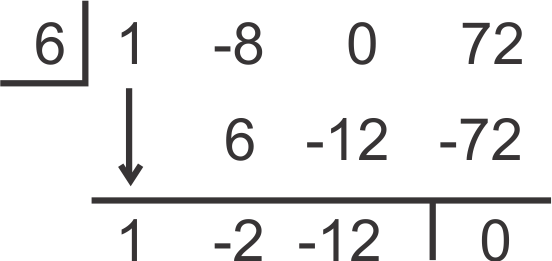Course: 6.10 多边合成科合成科

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 多多边合成科合成科

Collapse Expand
多多边合成科合成科
The volume of a rectangular prism is $\begin{aligned} 2 x^{3} + 5 x^{2} - x - 6 \end{aligned}$ . Determine if $\begin{aligned} 2 x + 3 \end{aligned}$ is the length of one of the prism's sides.
::矩形棱柱的体积为 2x3+5x2-x-6。确定 2x+3 是棱柱面的长度。

Synthetic Division
::合成司

Synthetic division is an alternative to long division . It can also be used to divide a polynomial by a possible factor , $\begin{aligned} x - k \end{aligned}$ . However, synthetic division cannot be used to divide larger , like quadratics, into another polynomial.
::合成分裂是长期分裂的替代物,也可以用它用一个可能的系数(x-k)来将多元分裂分开。但是,合成分裂不能用来将更大的象象象二次分裂一样的合成分裂分裂成另一个多边分裂。

Let's use synthetic division to divide $\begin{aligned} 2 x^{4} - 5 x^{3} - 14 x^{2} + 47 x - 30 \end{aligned}$ by $\begin{aligned} x - 2 \end{aligned}$ .
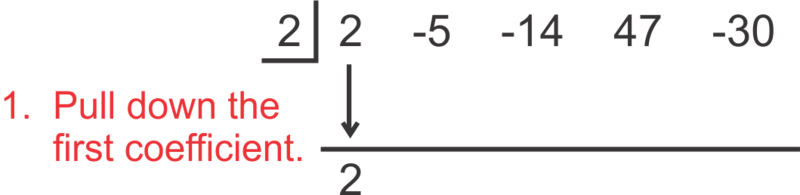
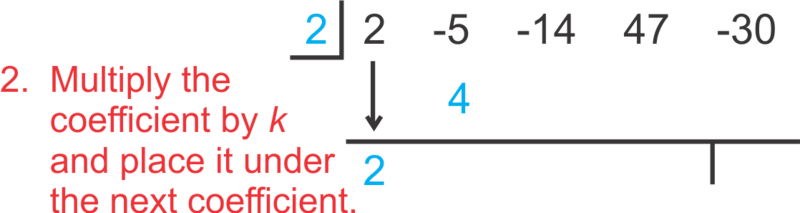
::让我们使用合成分区来将 2x4 - 5x3 - 14x2+47x- 30 除以 x-2 。

Using synthetic division, the setup is as follows:
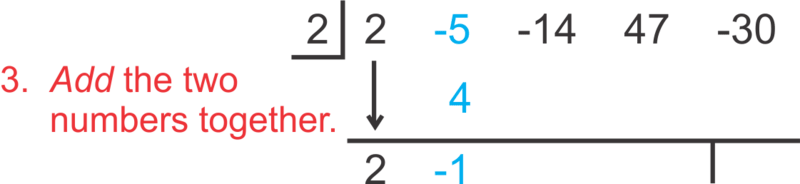
::利用合成部门,设置如下:

To “read” the answer, use the numbers as follows:
::在“阅读”答案时,使用以下数字:

Therefore , 2 is a solution, because the remainder is zero. The factored polynomial is $\begin{aligned} 2 x^{3} - x^{2} - 16 x + 15 \end{aligned}$ . Notice that when we synthetically divide by $\begin{aligned} k \end{aligned}$ , the “leftover” polynomial is one degree less than the original. We could also write $\begin{aligned} (x - 2) (2 x^{3} - x^{2} - 16 x + 15) = 2 x^{4} - 5 x^{3} - 14 x^{2} + 47 x - 30 \end{aligned}$ .
::因此, 2 是一个解决方案, 因为剩余部分为零。系数多元值为 2x3 - x2 - 16x+15。注意当我们合成除以 k 时, “ 剩余” 多元值比原值低一度。我们还可以写入 (x-2)( 2x3 - x2 - 16x+15) = 2x4 - 5x3 - 14x2+47x- 30) 。

Now, let's determine if 4 is a solution to $\begin{aligned} f (x) = 5 x^{3} + 6 x^{2} - 24 x - 16 \end{aligned}$ .
::现在,让我们来决定 F( x) = 5x3+6x2- 24x- 16 是否是 F( x) = 5x3+6x2- 24x- 16 的解决方案。

Using synthetic division, we have:
::利用合成分区,我们有:

The remainder is 304, so 4 is not a solution. Notice if we substitute in $\begin{aligned} x = 4 \end{aligned}$ , also written $\begin{aligned} f (4) \end{aligned}$ , we would have $\begin{aligned} f (4) = 5 (4)^{3} + 6 (4)^{2} - 24 (4) - 16 = 304 \end{aligned}$ . This leads us to the Remainder Theorem .
::其余为 304, 因此 4 不是一个解决方案。如果我们替换 x= 4 , 通知将使用 f(4)= 5(4)3+6(4)2- 24(4)- 16= 304。这让我们找到残余理论。

Remainder Theorem: If $\begin{aligned} f (k) = r \end{aligned}$ , then $\begin{aligned} r \end{aligned}$ is also the remainder when dividing by $\begin{aligned} (x - k) \end{aligned}$ .
::保留定理: 如果 f(k) =r, 当除以 (x-k) 时, r 也代表剩余。

This means that if you substitute in $\begin{aligned} x = k \end{aligned}$ or divide by $\begin{aligned} k \end{aligned}$ , what comes out of $\begin{aligned} f (x) \end{aligned}$ is the same. $\begin{aligned} r \end{aligned}$ is the remainder, but it is also the corresponding $\begin{aligned} y - \end{aligned}$ value. Therefore, the point $\begin{aligned} (k, r) \end{aligned}$ would be on the graph of $\begin{aligned} f (x) \end{aligned}$ .
::这意味着,如果您用 x=k 或除以 k 来替代 x=k 或除以 k, f( x) 中产生的内容是相同的。 r 是剩余部分, r 也是相应的 y- value。因此, 点( k,r) 将会在 f( x) 的图形中。

Finally, let's determine if $\begin{aligned} (2 x - 5) \end{aligned}$ is a factor of $\begin{aligned} 4 x^{4} - 9 x^{2} - 100 \end{aligned}$ .
::最后,让我们来判断一下(2x-5)是否是4x4-9x2-100的因数。

If you use synthetic division, the factor is not in the form $\begin{aligned} (x - k) \end{aligned}$ . We need to solve the possible factor for zero to see what the possible solution would be. Therefore, we need to put $\begin{aligned} \frac{5}{2} \end{aligned}$ up in the left-hand corner box. Also, not every term is represented in this polynomial. When this happens, you must put in zero placeholders. In this problem, we need zeros for the $\begin{aligned} x^{3} - \end{aligned}$ term and the $\begin{aligned} x - \end{aligned}$ term.
::如果您使用合成分区, 则该系数不是以( x- k) 的形式( x- k) 。我们需要解决零的可能系数, 才能看出可能的解决办法是什么。因此, 我们需要在左手角框中设置52 个。另外, 也不是每个词都代表在这个多面体中。发生这种情况时, 您必须设置零占位符。在此问题上, 我们需要为 x3- term 和 x- term 设定零。

This means that $\begin{aligned} \frac{5}{2} \end{aligned}$ is a zero and its corresponding binomial , $\begin{aligned} (2 x - 5) \end{aligned}$ , is a factor.
::这意味着52是零,其相应的二进制(2x-5)是一个因素。

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine if $\begin{aligned} 2 x + 3 \end{aligned}$ is the length of one of the prism's sides.
::早些时候,你被要求确定 2x+3 是否是棱镜侧的长度。

If $\begin{aligned} 2 x + 3 \end{aligned}$ divides evenly into $\begin{aligned} 2 x^{3} + 5 x^{2} - x - 6 \end{aligned}$ then it is the length of one of the prism's sides.
::如果 2x+3 均分分为 2x3+5x2-x-6, 那么它就是棱镜侧的长度。

If we want to use synthetic division, notice that the factor is not in the form $\begin{aligned} (x - k) \end{aligned}$ . Therefore, we need to solve the possible factor for zero to see what the possible solution would be. If $\begin{aligned} 2 x + 3 = 0 \end{aligned}$ then $\begin{aligned} x = - \frac{3}{2} \end{aligned}$ . Therefore, we need to put $\begin{aligned} \frac{- 3}{2} \end{aligned}$ up in the left-hand corner box.
::如果我们想要使用合成分解, 请注意该系数不是以( x- k) 的形式出现。因此, 我们需要解决零的可能系数, 才能看出可能的解决方案是什么。如果 2x+3=0, 那么 x32 。因此, 我们需要在左侧角框中放置 - 32 。

When we perform the synthetic division, we get a remainder of 0. This means that $\begin{aligned} (2 x + 3) \end{aligned}$ is a factor of the volume. Therefore, it is also the length of one of the sides of the rectangular prism.
::当我们执行合成分裂时,我们得到的剩余值为0。这意味着(2x+3)是体积的一个系数。因此,它也是矩形棱柱的一边的长度。

Example 2
::例2

Divide $\begin{aligned} x^{3} + 9 x^{2} + 12 x - 27 \end{aligned}$ by $\begin{aligned} (x + 3) \end{aligned}$ . Write the resulting polynomial with the remainder (if there is one).
::除以 x3+9x2+12x-27 到 (x+3) 。将结果的多义与剩余部分( 如果有的话) 一起写入。

Using synthetic division, divide by -3.
::使用合成分除法,除以-3。

The answer is $\begin{aligned} x^{2} + 6 x - 6 - \frac{9}{x + 3} \end{aligned}$ .
::答案为 x2+6x- 6- 9x+3。

Example 3
::例3

Divide $\begin{aligned} 2 x^{4} - 11 x^{3} + 12 x^{2} + 9 x - 2 \end{aligned}$ by $\begin{aligned} (2 x + 1) \end{aligned}$ . Write the resulting polynomial with the remainder (if there is one).
::以 2x+1 除以 2x4- 11x3+12x2+9x-2 。

Using synthetic division, divide by $\begin{aligned} - \frac{1}{2} \end{aligned}$ .
::使用合成分除法,除以-12。

The answer is $\begin{aligned} 2 x^{3} - 12 x^{2} + 18 x - \frac{2}{2 x + 1} \end{aligned}$ .
::答案是 2x3- 12x2+18x- 22x+1。

Example 4
::例4

Is 6 a solution for $\begin{aligned} f (x) = x^{3} - 8 x^{2} + 72 \end{aligned}$ ? If so, find the real-number zeros (solutions) of the resulting polynomial.
::6 是 f( x) =x3- 8x2+72 的解决方案吗 ? 如果是的话, 请找到结果的多元性的实际数字零( 解决方案) 。

Put a zero placeholder for the $\begin{aligned} x - \end{aligned}$ term. Divide by 6.
::x- 期数设置一个零占位符。除以 6 。

The resulting polynomial is $\begin{aligned} x^{2} - 2 x - 12 \end{aligned}$ . While this quadratic does not factor, we can use the Quadratic Formula to find the other roots.
::由此产生的多面体为 x2-2x-12。虽然此二次方块不因子, 但是我们可以使用二次方块来找到其他根。

$\begin{aligned} x = \frac{2 \pm \sqrt{2^{2} - 4 (1) (- 12)}}{2} = \frac{2 \pm \sqrt{4 + 48}}{2} = \frac{2 \pm 2 \sqrt{13}}{2} = 1 \pm \sqrt{13} \end{aligned}$

::x=222-4(1)(-1-2)2=24+482=22132=113

The solutions to this polynomial are 6, $\begin{aligned} 1 + \sqrt{13} \approx 4.61 \end{aligned}$ and $\begin{aligned} 1 - \sqrt{13} \approx - 2.61 \end{aligned}$ .
::这一多元性的解决办法是6, 1+134.61和1-132.61。

Review
::回顾

Use synthetic division to divide the following polynomials. Write out the remaining polynomial.
::使用合成分裂法来分割以下多面体。写出剩下的多面体。

$\begin{aligned} (x^{3} + 6 x^{2} + 7 x + 10) \div (x + 2) \end{aligned}$
:x3+6x2+7x+10) (x+2)

$\begin{aligned} (4 x^{3} - 15 x^{2} - 120 x - 128) \div (x - 8) \end{aligned}$
:4x3 - 15x2 - 120x - 128) (x-8)

$\begin{aligned} (4 x^{2} - 5) \div (2 x + 1) \end{aligned}$
:4x2 - 5) (2x+1)

$\begin{aligned} (2 x^{4} - 15 x^{3} - 30 x^{2} - 20 x + 42) \div (x + 9) \end{aligned}$
:2x4-15x3-30x2-20x+42)(x+9)

$\begin{aligned} (x^{3} - 3 x^{2} - 11 x + 5) \div (x - 5) \end{aligned}$
:x3-3x2-11x+5) (x-5)

$\begin{aligned} (3 x^{5} + 4 x^{3} - x - 2) \div (x - 1) \end{aligned}$
:3x5+4x3-x-2) (x-1)

Which of the division problems above generate no remainder? What does that mean?
::上述哪些分歧问题没有剩余?这是什么意思?

What is the difference between a zero and a factor?
::零和因数之间的差别是什么?

Find $\begin{aligned} f (- 2) \end{aligned}$ if $\begin{aligned} f (x) = 2 x^{4} - 5 x^{3} - 10 x^{2} + 21 x - 4 \end{aligned}$ .
::如果 f( x) = 2x4 - 5x3 - 10x2+21x- 4, 则查找 f(-2) 。

Now, divide $\begin{aligned} 2 x^{4} - 5 x^{3} - 10 x^{2} + 21 x - 4 \end{aligned}$ by $\begin{aligned} (x + 2) \end{aligned}$ synthetically. What do you notice?
::合成方式将 2x4- 5x3- 10x2+21x-4 除以 (x+2) 。您注意到什么 ?

Find all real zeros of the following polynomials, given one zero.
::查找以下多边协议的所有实际零, 给以零。

$\begin{aligned} 12 x^{3} + 76 x^{2} + 107 x - 20; - 4 \end{aligned}$
::12x3+76x2+107x-20;-4

$\begin{aligned} x^{3} - 5 x^{2} - 2 x + 10; - 2 \end{aligned}$
::x3 - 5x2 - 2x+10;-2

$\begin{aligned} 6 x^{3} - 17 x^{2} + 11 x - 2; 2 \end{aligned}$
::6x3-17x2+11x-2;2

Find all real zeros of the following polynomials, given two zeros.
::查找以下多边协议的所有实际零, 给两个零。

$\begin{aligned} x^{4} + 7 x^{3} + 6 x^{2} - 32 x - 32; - 4, - 1 \end{aligned}$
::x4+7x3+6x2-32x-32;-4-1

$\begin{aligned} 6 x^{4} + 19 x^{3} + 11 x^{2} - 6 x; 0, - 2 \end{aligned}$
::6x4+19x3+11x2-6x;0-2

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

多多边合成科合成科

Synthetic Division ::合成司

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Synthetic Division
::合成司

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)