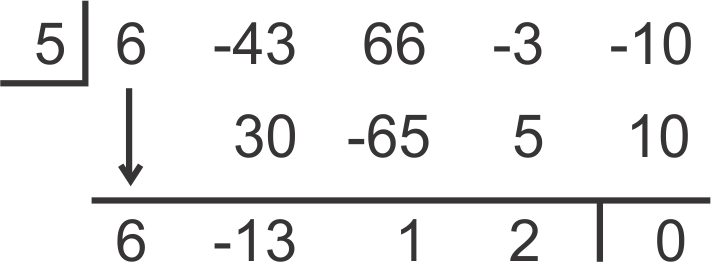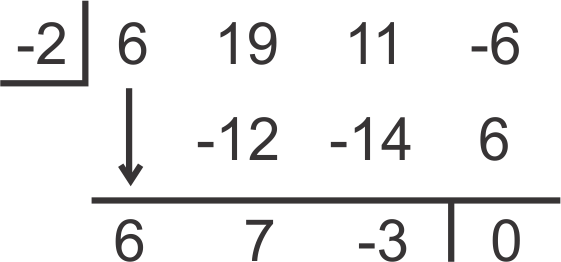6.11 合理和实际零调查

章节大纲

• 选择节常规

  折叠 展开

  常规

  全部折叠 展开全部

  • 选择活动新闻通告

    

    新闻通告 讨论区
• 选择节寻找合理和真实零

  折叠 展开

  寻找合理和真实零

  播放段落

  A length of a piece of farmland is $\begin{align*}2x^2 + 10\end{align*}$ and the width is $\begin{align*}x + 1\end{align*}$ . The area of the farmland is 353 square yards. What are the possible rational solutions to the polynomial equation represented by this situation?
  ::农田的长度是 2x2+10 ,宽度是 x+1 。 农田面积是 353 平方码。 以这种方式代表的多元等式的可能合理解决方案是什么 ?

  播放段落

  Rational and Real Zeros
  ::理性和现实零

  播放段落

  Recall that every quadratic equation has two solutions. The degree of a quadratic equation is 2, thus leading us towards the notion that it has 2 solutions. The degree will always tell us the maximum number of solutions a polynomial has. Quadratic equations also have a few different possibilities for solutions; two real-number solutions ( parabola passes through the $\begin{align*}x-\end{align*}$ axis twice), one real-number solution (where the solution is the vertex , called a repeated root), or two imaginary solutions (where the graph does not touch the $\begin{align*}x-\end{align*}$ axis at all).
  ::回顾每个二次方程都有两种解决办法。 二次方程的程度是 2 , 从而引导我们形成它有两种解决办法的概念。 度将始终告诉我们多元方程拥有的解决方案的最大数量。 二次方程也有一些不同的解决方案可能性; 两个真实数字解决方案( parabola通过 x - 轴两次 ) , 一个真实数字解决方案( 答案是顶端, 称为重复根 ) , 或两个假想解决方案( 图形根本没有触及 x - 轴 ) 。

  播放段落

  When it comes to solutions for , all these options are possibilities. There can be rational, irrational and imaginary solutions. Irrational and imaginary solutions will always come in pairs. This is due to the fact that to find these types of solutions, you must use the Quadratic Formula and the $\begin{align*}\pm\end{align*}$ sign will give two solutions. In this concept we will only address real-number solutions.
  ::当涉及到解决方案时,所有这些选项都是可能的。 可能有理性、 不合理和想象中的解决方案。 荒谬和想象中的解决方案总是同时出现。 这是因为要找到这些类型的解决方案, 您必须使用“ 二次曲线公式” , 而“ 符号” 将给出两种解决方案。 在这个概念中, 我们只处理实际数字解决方案 。

  播放段落

  Now, you might be wondering, how do we find all these solutions? One way is to use the Rational Root Theorem .
  ::现在,你可能想知道,我们如何找到所有这些解决方案?一种方法是使用理性根理论。

  播放段落

  Rational Root Theorem: For a polynomial, $\begin{align*}f(x)=a_nx^n+a_{n-1}x^{n-1}+ \cdots + a_1 x+a_0\end{align*}$ , where $\begin{align*}a_n, a_{n - 1}, \cdots a_0\end{align*}$ are integers , the rational roots can be determined from the factors of $\begin{align*}a_n\end{align*}$ and $\begin{align*}a_0\end{align*}$ . More specifically, if $\begin{align*}p\end{align*}$ is a factor of $\begin{align*}a_0\end{align*}$ and $\begin{align*}q\end{align*}$ is a factor of $\begin{align*}a_n\end{align*}$ , then all the rational factors will have the form $\begin{align*}\pm \frac{p}{q}\end{align*}$ .
  ::理性根理理论:对于一个多边分子, f(x) = anxn+an- 1xn-1a1x+a0, 如果一个, an- 1, @a1,\a1x+a0 是整数, 理性根可以由 an 和 a0 的因素来决定。 更具体地说, 如果 p 是 a0 的因数, q 是 a的因数, 那么所有理性因素都将具有 +pq 的形式 。

  播放段落

  In other words, the factors of the constant divided by the factors of the leading coefficient will yield all the possible rational solutions to $\begin{align*}f(x)\end{align*}$ .
  ::换句话说,不变系数除以主要系数因素的因素,将使f(x)产生所有可能的合理解决办法。

  播放段落

  Find all the possible rational solutions to $\begin{align*}f(x)=6x^4-43x^3+66x^2-3x-10\end{align*}$ .
  ::查找 f( x) = 6x4 - 43x3+66x2 - 3x- 10 的所有可能的理性解决方案。

  播放段落

  All the possible factors of 10 are 1, 2, 5, and 10. All the possible factors of 6 are 1, 2, 3, and 6. The possible combinations are $\begin{align*}\frac{\pm 1. \pm 2, \pm 5, \pm 10}{\pm 1, \pm 2, \pm 3, \pm 6}=\pm 1, \pm \frac{1}{2}, \pm \frac{1}{3}, \pm \frac{1}{6}, \pm 2, \pm \frac{2}{3}, \pm 5, \pm \frac{5}{2}, \pm \frac{5}{3}, \pm \frac{5}{6}, \pm 10, \pm \frac{10}{3}\end{align*}$ . Therefore , there are 24 possibilities.
  ::所有可能的因素为1,2,5和10。 6的可能因素为1,2,3和6。 可能的组合是1,2,2,5,10,1,2,3,6,1,12,13,16,2,23,5,5,52,53,5,56,10,10,103。 因此,有24种可能性。

  播放段落

  Find the rational solutions to $\begin{align*}f(x)=6x^4-43x^3+66x^2-3x-10\end{align*}$ .
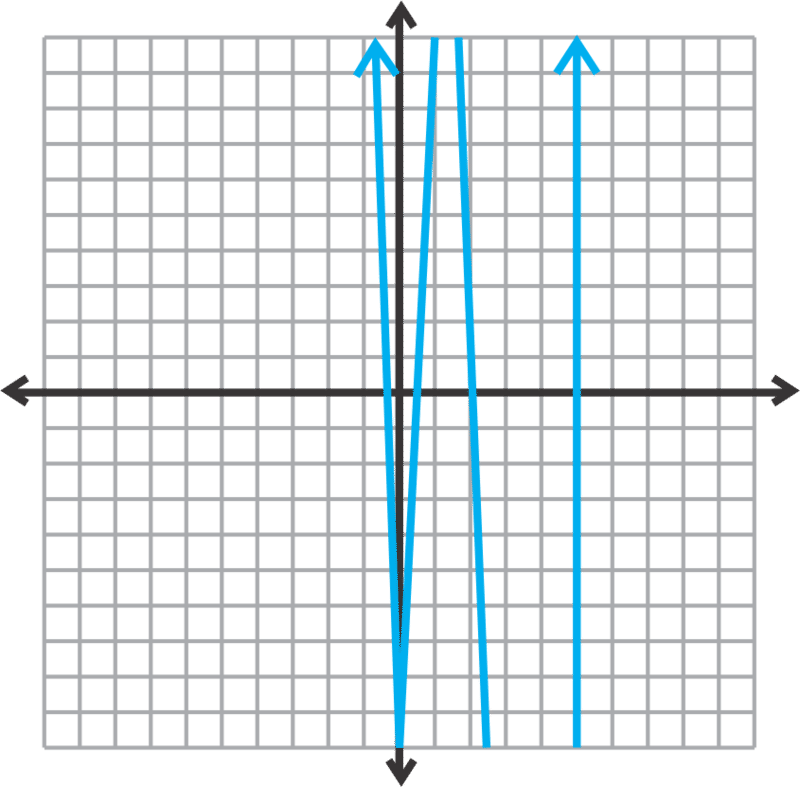
  ::查找 f( x) = 6x4 - 43x3+66x2 - 3x- 10 的合理解决方案。

  播放段落

  Before the days of graphing calculators, you would have to test all 24 possible solutions to find the correct solutions. Now, we can graph the function and eliminate any possibilities that seem unreasonable. Because the degree of the function is 4, there will be 4 solutions. Here is the graph:
  ::图形化计算器的几天前, 您必须测试所有24种可能的解决方案以找到正确的解决方案。 现在, 我们可以将函数图形化, 并消除任何看起来不合理的可能性 。 因为函数的大小是 4, 将会有 4 个解决方案 。 以下是图表 :

  

  播放段落

  Looking back at #1, the reasonable solutions appear to be: $\begin{align*}5, 2, \pm \frac{1}{2}, \pm \frac{1}{3}, \pm \frac{1}{6}, \pm \frac{2}{3}\end{align*}$ , or $\begin{align*}\pm \frac{5}{6}\end{align*}$ . By just looking at the graph, the solutions between -1 and 1 are difficult to see. This is why we have listed all the solutions between -1 and 1 to test. Let’s test 5 and 2 using synthetic division .
  ::回想1号,合理的解决方案似乎是:5,2,12,13,16,23 或 /56。只要看看图表,-1和1之间的解决方案就很难看出来。这就是为什么我们列出了1和1之间的所有解决方案来测试。让我们用合成分解来测试5和2。

  

  播放段落

  The remainder is zero, like we thought.
  ::剩下的是零,就像我们想的。

  播放段落

  Now, rather than starting over with the division by 2, continue with the leftover polynomial.
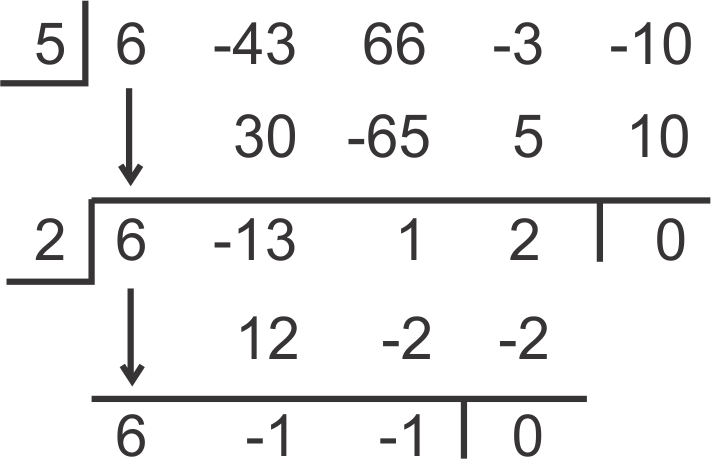
  ::现在,不要从二分开始,而是从二分开始, 继续用剩下的多面体。

  

  播放段落

  Again, the remainder is zero. Both 5 and 2 are zeros .
  ::其余为零,5和2均为零。

  播放段落

  To find the last two zeros, we can test all the fractions above using synthetic division. OR, we can factor this leftover polynomial. Because we started with a polynomial of degree 4, this leftover polynomial is a quadratic. It is $\begin{align*}6x^2-x-1. \ ac = -6\end{align*}$ and the factors of -1 that add up to -6 are -3 and 2. Expand the $\begin{align*}x-\end{align*}$ term and .
  ::为了找到最后两个零, 我们可以使用合成分解来测试上面所有的分数。 OR, 我们可以将这个剩余多位数乘以。 因为我们从一个4度的多位数开始, 这个剩余多位数是一个四边形。 这是 6x2 - x - 1. ac\6 和 - 1 的系数, 总计 - 6 和 2 的系数是 - 3 和 2 。 扩展 x - 期和 2 。

  播放段落

  $$\begin{align*}& \underbrace{6x^2-3x}+\underbrace{2x-1}\\ & 3x(2x-1)+1(2x-1)\\ & (2x-1)(3x+1)\end{align*}$$
  ::6x2 - 3x%2x1 - 1x3x(2x-1)+1(2x-1)(2x-1)(3x+1)

  播放段落

  Setting these two factors equal to zero, we have $\begin{align*}x=\frac{1}{2}\end{align*}$ and $\begin{align*}-\frac{1}{3}\end{align*}$ . Therefore, the solutions to this polynomial are 5, 2, $\begin{align*}\frac{1}{2}\end{align*}$ and $\begin{align*}-\frac{1}{3}\end{align*}$ .
  ::将这两个因素设定为零,我们有x=12和-13。因此,这一多元性的解决办法是5、2、12和-13。

  播放段落

  Check your answer: To check your work, you can multiply the factors together to see if you get the original polynomial.
  ::检查您的答案 : 要检查您的工作, 您可以将各种因素一起乘以查看您是否获得了 原始的多面性 。

  播放段落

  $$\begin{align*}& \underbrace{(2x-1)(3x+1)} \underbrace{(x-5)(x-2)}\\ & (6x^2-x-1)(x^2-7x+10)\\ & 6x^4-43x^3+66x^2-3x-10\end{align*}$$
  :2x-1)(3x+1) (x-5)(x-2) (6x2-x-1)(x2-7x+10) ×6x4-43x3+66x2-3x-10)

  播放段落

  Find all the real solutions to $\begin{align*}f(x)=x^4+6x^3-2x^2-48x-32\end{align*}$ .
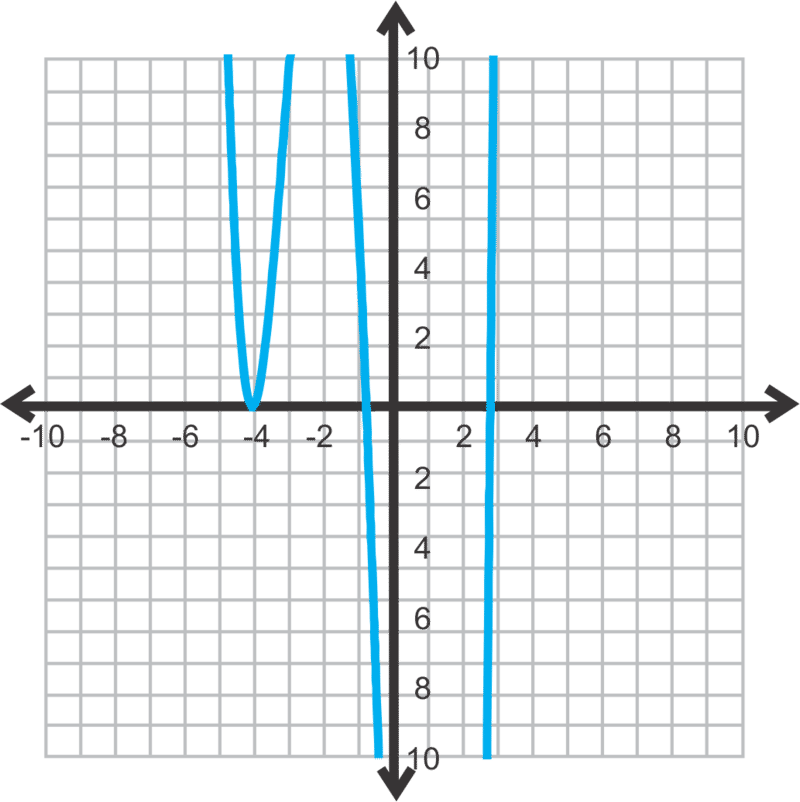
  ::查找 f( x) =x4+6x3-2x2- 48x-32 的所有真实解决方案。

  播放段落

  First, sketch a graph.
  ::首先,绘制一张图表。

  

  播放段落

  Now, use the Rational Root Theorem to determine all possible rational roots.
  ::现在,使用理性根理论来确定所有可能的理性根。

  播放段落

  $$\begin{align*}\frac{\text{factors of -32}}{\text{factors of 1}}=\frac{\pm 32, \pm 16, \pm 8, \pm 4, \pm 2, \pm 1}{\pm 1}\end{align*}$$
  ::-32因子1°32,16°16,8°8,4°4,2°2,1°1

  播放段落

  Using the graph, it looks like -4 is the only possible rational solution. Also, notice that the graph touches at -4 and does not pass through the $\begin{align*}x-\end{align*}$ axis. That means that this solution is a repeated root. Let’s do synthetic division.
  ::使用该图,它看起来像是 - 4 是唯一可能的理性解决方案。 另外,注意该图在 - 4 点接触,而不是通过 x - 轴。 这意味着这个解决方案是一个重复的根根。 让我们进行合成分解 。

  

  播放段落

  Because the root is repeated, we did synthetic division twice. At the end of the synthetic division, the leftover polynomial is $\begin{align*}x^2-2x-2\end{align*}$ which is not factorable. Therefore, to find the last two real solutions, we must do the Quadratic Formula.
  ::因为根是重复的, 我们做了两次合成分解。 在合成分解结束时, 剩下的多面体是 X2 - 2x - 2 , 不可考虑。 因此, 要找到最后两个真实的解决方案, 我们必须使用二次公式 。

  播放段落

  $$\begin{align*}x &= \frac{2 \pm \sqrt{(-2)^2-4(1)(-2)}}{2(1)}\\ &= \frac{2 \pm \sqrt{4+8}}{2}=\frac{2 \pm \sqrt{12}}{2}=\frac{2 \pm 2\sqrt{3}}{2}=1 \pm \sqrt{3} \approx 2.73, -0.73\end{align*}$$
  ::x=2______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

  播放段落

  The roots, or zeros, of $\begin{align*}f(x)=x^4+6x^3-2x^2-48x-32\end{align*}$ are -4 (twice), 2.73, and -0.73. Looking back at the graph, we see that this is where the function crosses the $\begin{align*}x-\end{align*}$ axis. The graph is always a good way to double-check your work.
  ::f(x) =x4+6x3-2x2- 48x-32的根或零是-4(两次)、 2.73 和- 0.73。回顾图时,我们看到,这是函数交叉 x- 轴的地方。图表总是检查你工作的好方法。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find  the possible rational solutions to the polynomial equation if the length of a piece of farmland is  $\begin{align*}2x^2+10\end{align*}$ , the width is  $\begin{align*}x+1\end{align*}$ , and the area is 353 square yards.
  ::早些时候,有人要求你找到多元等式的可能合理解决方案,如果一块农田的长度为2x2+10,宽度为x+1,而面积为353平方码。

  播放段落

  First, we need to set up the equation.
  ::首先,我们需要设置方程。

  播放段落

  $$\begin{align*}(x + 1)(2x^2 + 10) = 353\\ = 2x^3 + 10x + 2x^2 + 10 = 353\\ = 2x^3 + 2x^2 + 10x - 343 = 0\end{align*}$$
  :x+1)(2x2+10)=353=2x3+103+10x2+103=353=2x3+2x2+10=2x3+2x2+10x3=0

  播放段落

  All the possible factors of 343 are 1, 7, 49, and 343. All the possible factors of 2 are 1 and 2. The possible combinations are $\begin{align*}\frac{\pm 1, \pm 7, \pm 49, \pm 343}{\pm 1, \pm 2}=\pm 1, \pm 7, \pm 49, \pm 343, \pm \frac{1}{2}, \pm \frac{7}{2}, \pm \frac{49}{2}, \pm \frac{343}{2}\end{align*}$ . Therefore, there are 16 possibilities.
  ::343的所有可能因素为1,7,49和343,2个可能因素为1,2个可能因素为2,2个可能因素为1,1,7,7,49,343,1,2,1,7,7,49,4,4,4,4,4,4,4,4,7,4,4,4,4,4,4,7,7,72,4,492,3432,因此,有16种可能性。

  播放段落

  Example 2
  ::例2

  播放段落

  Find all the real solutions: $\begin{align*}f(x)=x^3-2x^2-15x+30\end{align*}$
  ::查找所有真实的解决方案 : f( x) =x3 - 2x2 - 15x+30

  播放段落

  Using the Rational Root Theorem, the possible rational roots are: $\begin{align*}\pm 30, \pm 15, \pm 10, \pm 6, \pm 5, \pm 3, \pm 2, \pm 1\end{align*}$ . Now, graph the function.
  ::使用理性根理论, 可能的合理根是 : 30, 15, 10, 6, 5, 3, 3, 2, 1. 现在, 请绘制函数 。

  

  播放段落

  By looking at the graph, the only reasonable rational root is 2. We can rule out 4 and -4 because they are not included in the list of rational roots. Therefore, these two roots will be irrational. Do the synthetic division for 2.
  ::通过查看图表,唯一合理的合理根根是2,我们可以排除4和4,因为它们没有被列入合理根清单。因此,这两个根将是非理性的。做2个合成分解。

  

  播放段落

  The leftover polynomial is $\begin{align*}x^2-15=0\end{align*}$ . This polynomial can be solved by using square roots.
  ::剩余多面性为 x2- 15= 0。 此多面性可以通过平方根解决 。

  播放段落

  $$\begin{align*}x^2-15 &= 0\\ x^2 &= 15\\ x &= \pm \sqrt{15} \approx \pm 3.87\end{align*}$$
  ::x2 - 15=0x2=15x_ @ @ @ 15_ @ @ 3_ 3. 87

  播放段落

  $\begin{align*}^*\end{align*}$ Instead of using the Rational Root Theorem and synthetic division, this problem could have also been solved using factoring by grouping .
  ::* 不使用有理的根理论和合成分解,这个问题本来也可以通过分组的保理来加以解决。

  播放段落

  Example 3
  ::例3

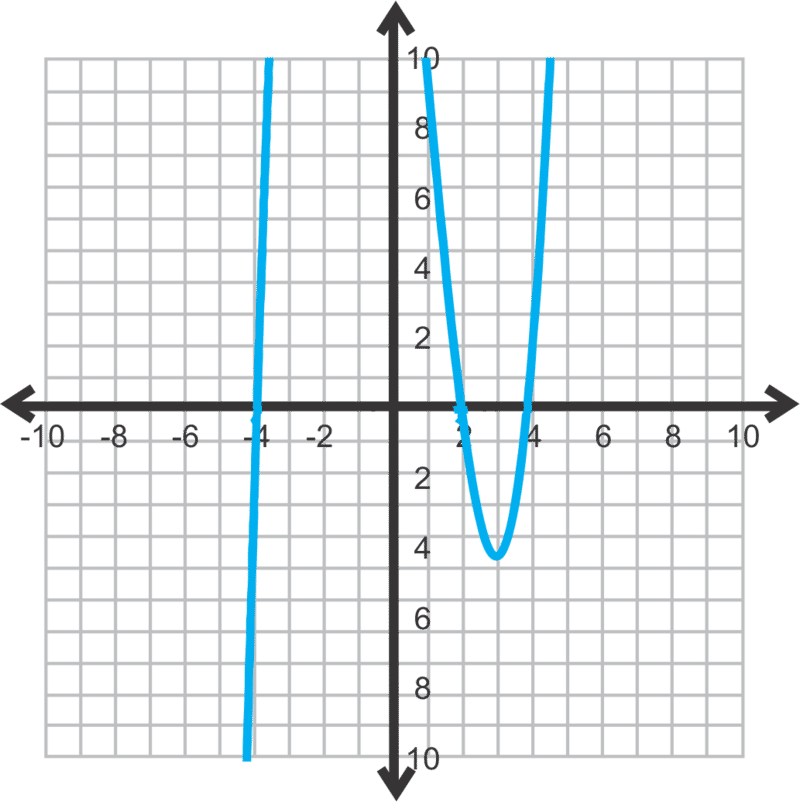
  播放段落

  Find all the real solutions: $\begin{align*}f(x)=6x^3+19x^2+11x-6\end{align*}$
  ::查找所有真实的解决方案 : f( x)=6x3+19x2+11x-6

  播放段落

  Using the Rational Root Theorem, the possible rational roots are: $\begin{align*}\pm 6, \pm 3, \pm 2, \pm \frac{3}{2}, \pm 1, \pm \frac{1}{2}, \pm \frac{1}{3}, \pm \frac{1}{6}\end{align*}$ .
  ::使用理性根理论,可能的合理根源是:6,3,3,2,3,3,3,3,1,1,12,13,16。

  

  播放段落

  By looking at the graph, the reasonable rational roots are $\begin{align*}-2, -\frac{3}{2}, \frac{1}{3}\end{align*}$ or $\begin{align*}\frac{1}{6}\end{align*}$ . The rational answers are difficult to see because they do not cross exactly the $\begin{align*}x-\end{align*}$ axis on an integer. Therefore, we will do the synthetic division for -2 first.
  ::通过查看图表,合理的合理根根是-2,-32,13或16。 合理的答案很难看出来,因为它们没有完全跨越一个整数上的X-轴。 因此,我们将首先对-2进行合成分解。

  

  播放段落

  The leftover polynomial is $\begin{align*}6x^2+7x-3\end{align*}$ , which is factorable. You can decide if you would like to factor this polynomial, use the Quadratic Formula, or test the rational possibilities from above. Let’s factor.
  ::剩余多面体为 6x2+7x- 3 , 这是可以计算的因素 。 您可以决定您是否想要乘以此多面体, 使用二次曲线公式, 或者测试上面的合理可能性 。

  播放段落

  $$\begin{align*}& 6x^2+7x-3\\ & 6x^2+9x-2x-3\\ & 3x(2x+3)-1(2x+3)\\ & (3x-1)(2x+3)\end{align*}$$
  ::6x2+7x-36x2+9x-2x-33xx(2xx+3)-1(2x+3)(3x-1)(2x+3)

  播放段落

  From these factors, the rational solutions are $\begin{align*}\frac{1}{3}\end{align*}$ and $\begin{align*}-\frac{3}{2}\end{align*}$ .
  ::从这些因素来看,合理的解决办法是13个和-32个。

  播放段落

  Example 4
  ::例4

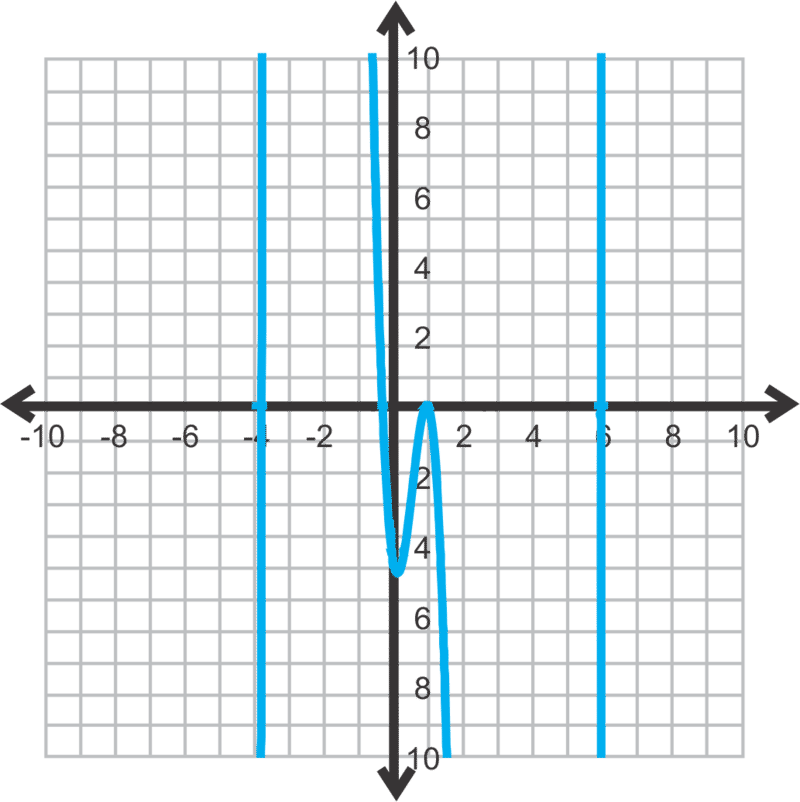
  播放段落

  Find all the real solutions: $\begin{align*}f(x)=x^5-4x^4-18x^3+38x^2-11x-6\end{align*}$
  ::查找所有真实的解决方案 : f( x) =x5- 4x4- 18x3+38x2- 11x- 6

  播放段落

   Using the Rational Root Theorem, the possible rational roots are: $\begin{align*}\pm 6, \pm 3, \pm 2, \pm 1\end{align*}$ .
  ::使用理性根理论,可能的合理根源是:6,3,3,2,1。

  

  播放段落

  From the graph, the possible roots are 6 and 1. It looks like 1 is a double root because the function reaches the $\begin{align*}x-\end{align*}$ axis at 1, but does not pass through it. Do synthetic division with 6, 1, and 1 again.
  ::从图中看,可能的根源是 6 和 1 。 它看起来像 1 是一个双根, 因为函数在 1 时到达 x - 轴, 但不能通过它。 再用 6, 1 和 1 进行合成分解 。

  

  播放段落

  The leftover polynomial is $\begin{align*}x^2+4x+1\end{align*}$ . This is not a factorable polynomial, so use the Quadratic Formula to find the last two roots.
  ::剩余多面体为 x2+4x+1。 这不是一个可因数的多面体, 所以使用二次曲线公式来找到最后两个根 。

  播放段落

  $$\begin{align*}x=\frac{-4 \pm \sqrt{4^2-4(1)(1)}}{2(1)}=\frac{-4 \pm \sqrt{12}}{2}=\frac{-4 \pm 2\sqrt{3}}{2}=-2 \pm \sqrt{3} \approx -0.27, -3.73\end{align*}$$
  ::4444442222230.27,-3.73

  播放段落

  Review
  ::回顾

  播放段落

  Find all the possible rational solutions for the following polynomials. Use the Rational Root Theorem.
  ::为以下多边协议寻找所有可能的理性解决方案。 使用理性根理论 。

  播放段落
  1. $\begin{align*}f(x)=x^3+6x^2-18x+20\end{align*}$
     :x) =x3+6x2-18x+20
  播放段落
  2. $\begin{align*}f(x)=4x^4+x^2-15\end{align*}$
     :xx)=4x4+x2-15)
  播放段落
  3. $\begin{align*}f(x)=-2x^3+7x^2-x+8\end{align*}$
     :x) f=2x3+7x2 -x+8
  播放段落
  4. $\begin{align*}f(x)=x^4-3x^3-4x^2+15x+9\end{align*}$
     :x) =x4- 3x3- 4x2+15x+9
  播放段落
  5. $\begin{align*}f(x)=8x^4 -5x^3+16x^2+37x-24\end{align*}$
     :x) = 8x4 - 5x3+ 16x2+ 37x- 24

  播放段落

  Find all the real-number solutions for each function below. Use any method you like.
  ::查找以下每个函数的所有真实数字解决方案。使用任何您喜欢的方法。

  播放段落
  6. $\begin{align*}f(x)=6x^3-17x^2+11x-2\end{align*}$
     :x)=6x3-17x2+11x-2
  播放段落
  7. $\begin{align*}f(x)=x^4+7x^3+6x^2-32x-32\end{align*}$
     :x) =x4+7x3+6x2 - 32x-32
  播放段落
  8. $\begin{align*}f(x)=16x^3+40x^2-25x-3\end{align*}$
     :x) = 16x3+40x2- 25x-3
  播放段落
  9. $\begin{align*}f(x)=2x^3-9x^2+21x-18\end{align*}$
     :x) = 2x3- 9x2+21x- 18
  播放段落
  10. $\begin{align*}f(x)=4x^3-16x^2+39x-295\end{align*}$
      :x)=4x3-16x2+39x-295
  播放段落
  11. $\begin{align*}f(x)=18x^4+3x^3-17x^2+17x-55\end{align*}$
      ::f(x) = 18x4+3x3-17x2+17x5-55
  播放段落
  12. $\begin{align*}f(x)=x^5+7x^4-3x^3-65x^2-8x-156\end{align*}$
      :x) =x5+7x4-3x3-65x2-8x-156)
  播放段落
  13. $\begin{align*}f(x)=4x^4+20x^3-23x^2-120x+144\end{align*}$
      ::f(x) = 4x4+20x3 - 23x2 - 120x+144
  播放段落
  14. $\begin{align*}f(x)=9x^4-226x^2+25\end{align*}$
      :x)=9x4-226x2+25
  播放段落
  15. Solve $\begin{align*}f(x)=3x^4-x^2-14\end{align*}$ by factoring. How many real solutions does this function have? What type of solution(s) could the others be?
      ::以保理法解决 f( x) = 3x4- x2- 14 。 此函数有多少真正的解决方案? 其它的可以是什么类型的解决方案 ?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。