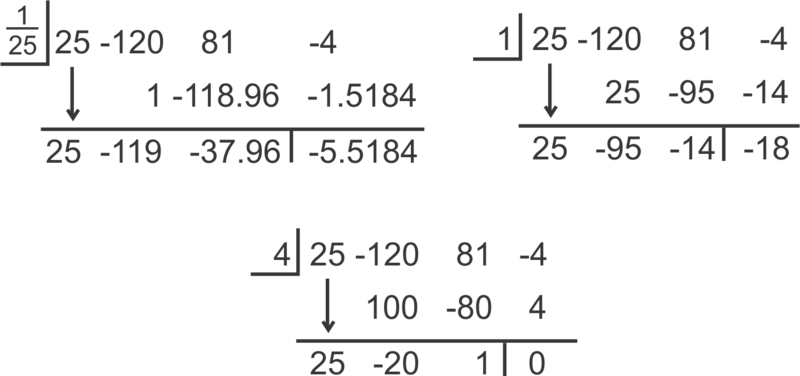Course: 6.12 寻找想象解决方案

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 寻找想象解决方案

Collapse Expand
寻找想象解决方案
Louis calculates that the area of a rectangle is represented by the equation $\begin{align*}3x^4 + 7x^2 = 2\end{align*}$ . Did Louis calculate it right? Explain based on the degree and zeros of the function .
::Louis 计算矩形区域代表方程式 3x4+7x2=2。 Louis 计算正确吗? 根据函数的度和零解释。

Imaginary Solutions
::想象解决方案

Remember, imaginary solutions always come in pairs. To find the imaginary solutions to a function, use the Quadratic Formula .
::记住, 想象中的解决方案总是一对一。要找到函数的假想解决方案, 请使用 Quadratic 公式。

Let's solve $\begin{align*}f(x)=3x^4-x^2-14\end{align*}$ .
::让我们解析 f( x) = 3x4 - x2 - 14 。

First, this quartic function can be factored just like a quadratic equation .
::首先,这个二次函数可以像二次方程一样被计算成二次方程。

$\begin{align*}g(x)=x^4+21x^2+90\end{align*}$
::g(x) =x4+21x2+90

Now, because neither factor can be factored further and there is no $\begin{align*}x-\end{align*}$ term , we can set each equal to zero and solve.
::现在,因为两个因素都无法进一步考虑,而且没有x-sterm,我们可以将每个因素设定为零,解决。

$\begin{aligned} 3 x^{2} - 7 = 0 \\ x^{2} + 2 = 0 & 3 x^{2} = 7 \\ x^{2} = - 2 a n d & x^{2} = \frac{7}{3} \\ x = \pm \sqrt{- 2} o r \pm i \sqrt{2} & x = \pm \sqrt{\frac{7}{3}} o r \pm \frac{\sqrt{21}}{3} \end{aligned}$
$\begin{align*}& && 3x^2-7=0\\ & x^2+2=0 && 3x^2=7\\ & x^2=-2 \qquad \qquad \qquad \quad and && x^2=\frac{7}{3}\\ & x=\pm \sqrt{-2} \ or \ \pm i \sqrt{2} && x=\pm \sqrt{\frac{7}{3}} \ or \ \pm \frac{\sqrt{21}}{3}\end{align*}$
::3x2 - 7= 0x2+2= 03x2= 7x2 @ @ 2andx2= 73x%2 或 i2x%73 或 213

Including the imaginary solutions, there are four, which is what we would expect because the degree of this function is four.
::包括假想的解决办法,有四个,这是我们所期望的,因为这一职能的程度是四个。

Now, let's find all the solutions of the function $\begin{align*}g(x)=x^4+21x^2+90\end{align*}$ .
::现在,让我们找到函数 g( x) =x4+21x2+90的所有解决方案。

When graphed, this function does not touch the $\begin{align*}x-\end{align*}$ axis. Therefore , all the solutions are imaginary. To solve, this function can be factored like a quadratic equation. The factors of 90 that add up to 21 are 6 and 15.
::图形化时,此函数不会触动 x - 轴。因此,所有解决方案都是想象的。要解决,此函数可以像二次方程一样计算。总计为21的90系数是6和15。

$\begin{aligned} g (x) & = x^{4} + 21 x^{2} + 90 \\ 0 & = (x^{2} + 6) (x^{2} + 15) \end{aligned}$
$\begin{align}g(x) &= x^4+21x^2+90\\ 0 &= (x^2+6)(x^2+15)\end{align}$
::g(x)=x4+21x2+900=(x2+6)(x2+15)

Now, set each factor equal to zero and solve.
::现在,设定每个系数等于零,然后解决。

$\begin{aligned} x^{2} + 6 = 0 & x^{2} + 15 = 0 \\ x^{2} = - 6 a n d & x^{2} = - 15 \\ x = \pm i \sqrt{6} & x = \pm i \sqrt{15} \end{aligned}$
$\begin{align*}& x^2+6=0 && x^2+15=0\\ & x^2=-6 \qquad \qquad \qquad and && x^2=-15\\ & x=\pm i \sqrt{6} && x=\pm i \sqrt{15}\end{align*}$
::x2+6 = 0x2+15= 0x2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\15\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

Finally, let's find the function that has the solution 3, -2, and $\begin{align*}4 + i\end{align*}$ .
::最后,让我们找到一个具有3,2和4+i解决方案的功能。

Notice that one of the given solutions involves an imaginary number. Imaginary and complex solutions always come in pairs, so $\begin{align*}4 - i\end{align*}$ is also a factor. The two factors are complex conjugates. Translate each solution into a factor and multiply them all together.
::请注意, 给定的解决方案之一包含一个虚构的数字。想象和复杂的解决方案总是同时出现, 因此 4- i 也是一个因素。这两个因素是复杂的共鸣。将每个解决方案转换成一个要素, 并一起乘以它们。

Any multiple of this function would also have these roots. For example, $\begin{align*}2x^4-18x^3+38x^2+62x-204\end{align*}$ would have these roots as well.
::此函数的任何多个函数也会有这些根。例如, 2x4-18x3+38x2+62x-204也会有这些根。

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine if Louis calculated his work correctly.
::早些时候,你被要求确定路易是否正确计算了他的作品

First we need to change the equation to standard form . Then we can factor it.
::首先我们要把方程式改成标准形式然后我们再考虑一下

$\begin{aligned} 3 x^{4} + 7 x^{2} & = 2 \\ 3 x^{4} + 7 x^{2} - 2 & = 0 \\ (3 x^{2} + 1) (x^{2} + 2) & = 0 \end{aligned}$
$\begin{align}3x^4 + 7x^2 &= 2\\ 3x^4 + 7x^2 - 2 &= 0\\ (3x^2 + 1)(x^2 + 2) &= 0 \end{align}$
::3x4+7x2=23x4+7x2-2=0(3x2+1)(x2+2)=0

Solving for x we get
::我们得到的x的溶解

$\begin{aligned} 3 x^{2} + 1 = 0 & x^{2} + 2 = 0 \\ x^{2} = \frac{- 1}{3} a n d & x^{2} = - 2 \\ x = \pm i \sqrt{\frac{1}{3}} & x = \pm i \sqrt{2} \end{aligned}$
$\begin{align*} 3x^2+1=0 && x^2+2=0\\ & x^2=\frac{-1}{3} \qquad \qquad \qquad and && x^2=-2\\ & x=\pm i \sqrt{\frac{1}{3}} && x=\pm i \sqrt{2}\end{align*}$
::3x2+1=0x2+2=0x2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\2\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

All of the solutions are imaginary and the area of a rectangle must have real solutions. Therefore Louis did not calculate correctly.
::所有解决方案都是虚构的,矩形区域必须有真正的解决方案,因此路易没有正确计算。

Example 2
::例2

Find all the solutions to the following function: $\begin{align*}f(x)=25x^3-120x^2+81x-4\end{align*}$ .
::查找以下函数的所有解决方案 : f( x) = 25x3 - 120x2+81x- 4 。

First, graph the function.
::首先,绘制函数图。

Using the Rational Root Theorem , the possible realistic zeros could be $\begin{align*}\frac{1}{25}\end{align*}$ , 1, or 4. Let’s try these three possibilities using synthetic division .
::使用理性根理论, 现实的零位可能为125、1或4, 让我们使用合成分解来尝试这三种可能性。

Of these three possibilities, only 4 is a zero. The leftover polynomial , $\begin{align*}25x^2-20x+1\end{align*}$ is not factorable, so we need to use the Quadratic Formula to find the last two zeros.
::在这三种可能性中,只有4种是零。剩余多面体, 25x2-20x+1是不可计数的, 所以我们需要使用二次曲线公式来找到最后两个零。

$\begin{aligned} x & = \frac{20 \pm \sqrt{20^{2} - 4 (25) (1)}}{2 (25)} \\ = \frac{20 \pm \sqrt{400 - 100}}{50} \\ = \frac{20 \pm 10 \sqrt{3}}{50} o r \frac{2 \pm \sqrt{3}}{5} \approx 0.746 a n d 0.054 \end{aligned}$
$\begin{align}x &= \frac{20 \pm \sqrt{20^2-4(25)(1)}}{2(25)}\\ &= \frac{20 \pm \sqrt{400-100}}{50}\\ &=\frac{20 \pm 10 \sqrt{3}}{50} \ or \ \frac{2 \pm \sqrt{3}}{5} \approx 0.746 \ and \ 0.054 \end{align}$
::x=20202-4(25)(1)(1)(2)(25)=20400-10050=2010350或2350.746和0.054

Helpful Hint: Always find the decimal values of each zero to make sure they match up with the graph.
::帮助提示: 总是找到每个零的十进制值, 以确保它们与图形匹配。

Example 3
::例3

Find all the solutions to the following function: $\begin{align*}f(x)=4x^4+35x^2-9\end{align*}$ .
::为以下函数查找所有解决方案: f( x)=4x4+35x2- 9。

$\begin{align*}f(x)=4x^4+35x^2-9\end{align*}$ is factorable. $\begin{align*}ac = -36\end{align*}$ .
::f(x) = 4x4+35x2- 9 可乘因数。 ac36。

$\begin{aligned} 4 x^{4} + 35 x^{2} - 9 \\ 4 x^{4} + 36 x^{2} - x^{2} - 9 \\ 4 x^{2} (x^{2} + 9) - 1 (x^{2} + 9) \\ (x^{2} + 9) (4 x^{2} - 1) \end{aligned}$
$\begin{align*} 4x^4+35x^2-9\\ 4x^4+36x^2-x^2-9\\ 4x^2(x^2+9)-1(x^2+9)\\ (x^2+9)(4x^2-1)\end{align*}$
::4x4+35x2-94x4+36x2-x2-94x2(x2+9)-1(x2+9)-(x2+9)-(x2+9)-(x2+9)-(4x2--1)

Setting each factor equal to zero, we have:
::确定每个系数等于零,我们有:

$\begin{aligned} 4 x^{2} - 1 = 0 \\ x^{2} + 9 = 0 & 4 x^{2} = 1 \\ x^{2} = - 9 o r & x^{2} = \frac{1}{4} \\ x = \pm 3 i & x = \pm \frac{1}{2} \end{aligned}$
$\begin{align*}& && 4x^2-1=0\\ & x^2+9=0 && 4x^2=1\\ & x^2=-9 \quad \qquad \qquad or && x^2=\frac{1}{4}\\ & x=\pm 3i && x=\pm \frac{1}{2}\end{align*}$
::4x2 - 1=0x2+9=04x2=1x2=1x29orx2=14x_%3ix#12

Example 4
::例4

Find the equation of a function with roots 4, $\begin{align*}\sqrt{2}\end{align*}$ and $\begin{align*}1-i\end{align*}$ .
::查找函数的等式, 根4、 2 和 1- i 。

Recall that irrational and imaginary roots come in pairs. Therefore, all the roots are 4, $\begin{align*}\sqrt{2}, {\color{red}-\sqrt{2}},1+i,{\color{red}1-i}\end{align*}$ . Multiply all 5 roots together.
::回顾不合理和想象中的根是双对的。因此,所有根都是4, 2, 2, 2, 1+i, 1-i。将所有5根并列在一起。

$\begin{aligned} (x - 4) (x - \sqrt{2}) (x + \sqrt{2}) (x - (1 + i)) (x - (1 - i)) \\ (x - 4) (x^{2} - 2) (x^{2} - 2 x + 2) \\ (x^{3} - 4 x^{2} - 2 x + 8) (x^{2} - 2 x + 2) \\ x^{5} - 6 x^{4} + 8 x^{3} - 4 x^{2} - 20 x + 16 \end{aligned}$
$\begin{align*} (x-4)(x-\sqrt{2})(x+\sqrt{2})(x-(1+i))(x-(1-i))\\ (x-4)(x^2-2)(x^2-2x+2)\\ (x^3-4x^2-2x+8)(x^2-2x+2)\\ x^5-6x^4+8x^3-4x^2-20x+16\end{align*}$
:x2-2)x5-6x4-8x3-20x+16)

Review
::回顾

Find all solutions to the following functions. Use any method.
::为以下函数寻找所有解决方案。使用任何方法。

$\begin{align*}f(x)=x^4+x^3-12x^2-10x+20\end{align*}$
:x) =x4+x3 - 12x2 - 10x+20

$\begin{align*}f(x)=4x^3-20x^2-3x+15\end{align*}$
:xx) = 4x3 - 20x2 - 3x+15

$\begin{align*}f(x)=2x^4-7x^2-30\end{align*}$
:xx) = 2x4 - 7x2 - 30

$\begin{align*}f(x)=x^3+5x^2+12x+18\end{align*}$
::f(x) =x3+5x2+12x18

$\begin{align*}f(x)=4x^4+4x^3-22x^2-8x+40\end{align*}$
:x)=4x4+4x3-22x2-8x+40

$\begin{align*}f(x)=3x^4+4x^2-15\end{align*}$
:x) = 3x4+4x2- 15

$\begin{align*}f(x)=2x^3-6x^2+9x-27\end{align*}$
:x) = 2x3- 6x2+9x- 27

$\begin{align*}f(x)=6x^4-7x^3-280x^2-419x+280\end{align*}$
:x) = 6x4 - 7x3 - 280x2 - 419x+280

$\begin{align*}f(x)=9x^4+6x^3-28x^2+2x+11\end{align*}$
:x)=9x4+6x3_28x2+2x+11

$\begin{align*}f(x)=2x^5-19x^4+30x^3+97x^2-260x+150\end{align*}$
::f(x) = 2x5 - 19x4+30x3+97x2 - 260x+150

Find a function with the following roots.
::查找含有以下根的函数。

$\begin{align*}4, i\end{align*}$
::4, i 4, i

$\begin{align*}-3, -2i\end{align*}$
::- 3,-2,i

$\begin{align*}\sqrt{5}, -1 + i\end{align*}$
::5-1+i 5-1+1

$\begin{align*}2, \frac{1}{3}, 4-\sqrt{2}\end{align*}$

Writing: Write down the steps you use to find all the zeros of a polynomial function.
::写入: 写下您用来查找多面函数的所有零的步数。

Writing: Why do imaginary and irrational roots always come in pairs?
::写道:为什么想象和非理性的根总是成对?

Challenge: Find all the solutions to $\begin{align*}f(x)=x^5+x^3+8x^2+8\end{align*}$ .
::挑战: 找到 f( x) =x5+x3+8x2+8的所有解决方案。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

寻找想象解决方案

Imaginary Solutions ::想象解决方案

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Imaginary Solutions
::想象解决方案

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)