Course: 6.13 寻找和界定多面函数图的部分

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

聚合函数图的查找和定义部分

The prototype for a roller coaster is represented by the equation $\begin{align*}y = x^5 - 8x^3 + 10x + 6\end{align*}$ . What is the maximum height the coaster will reach over the domain [-1, 2]?
::过山车原型由 y=x5-8x3+10x+6 等式表示。离山车在域上的最大高度是多少 [ - - - 2] ?

Parts of a Polynomial Graph
::圆形图部分

By now, you should be familiar with the general idea of what a polynomial function graph does. It should cross the $\begin{align*}x-\end{align*}$ axis as many times as the degree , unless there are imaginary solutions. It will curve up and down and can have a maximum and a minimum. Let’s define the parts of a polynomial function graph here.
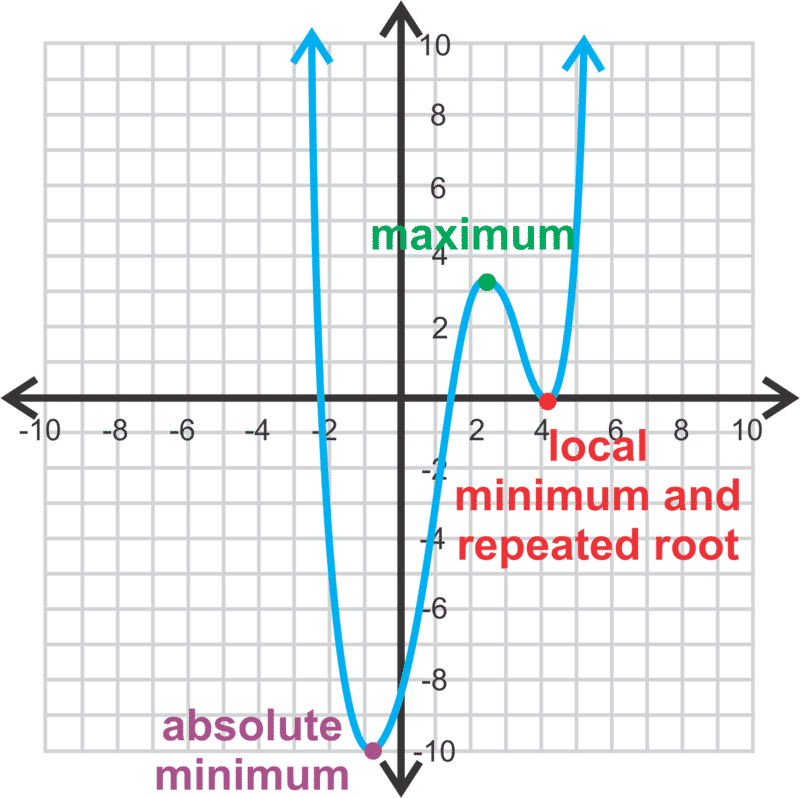
::现在,你应该熟悉多元函数图的通用概念。它应该比水平多出多少倍, 除非有想象的解决方案。它会向上或向下曲线, 并且可以有一个最大和最小的。让我们在这里定义一个多数值函数图的部位。

Notice that in both the cubic (third degree, on the left) and the quartic (fourth degree, on the right) functions, there is no vertex . We now have minimums and maximums. If there are more than one minimum or maximum, there will be an absolute maximum/minimum , which is the lowest/highest point of the graph. A local maximum/minimum is a maximum/minimum relative to the points around it. The places where the function crosses the $\begin{align*}x-\end{align*}$ axis are still the solutions (also called $\begin{align*}x-\end{align*}$ intercepts , roots or zeros). In the quartic function, there is a repeated root at $\begin{align*}x = 4\end{align*}$ . A repeated root will touch the $\begin{align*}x-\end{align*}$ axis without passing through or it can also have a “jump” in the curve at that point (see the first problem below). All of these points together (maximums, minimums, $\begin{align*}x-\end{align*}$ intercepts, and $\begin{align*}y-\end{align*}$ intercept) are called critical values.
::注意在立方(第三度,左侧)和二次(第四度,右侧)的函数中,没有顶点。我们现在有最小值和最大值。如果有一个以上最小值或最大值,则将有一个绝对最大/最小值,这是图中最低/最高点。本地最大/最小值是相对于其周围点的最大/最小值。函数横跨 x- 轴的最大/最小值仍然是解决方案(也称为 X- 界面、根或零) 。在二次函数中,在 x= 4 上有一个重复根。重复的根将不经过x- 轴,或者在那个点上也可以在曲线中有一个“ 跳动 ” (见下文第一个问题)。所有这些点(最大、最小值、 x- intercys 和 y- intercept) 统统称为关键值。

Another important thing to note is end behavior. It is exactly what it sounds like; how the “ends” of the graph behaves or points. The cubic function above has ends that point in the opposite direction. We say that from left to right, this function is mostly increasing. The quartic function’s ends point in the same direction, both positive, just like a quadratic function . When considering end behavior, look at the leading coefficient and the degree of the polynomial .
::需要注意的另一个重要问题是结束行为。它恰恰是它听起来像什么;图形的“结束”行为或点如何。上面的立方函数以相反的方向结束。我们说,从左到右,这个函数大多在增加。二次函数的终点指向同一方向,两者都是正的,就像二次函数一样。在考虑结束行为时,请看主要系数和多位数的程度。

Let's use a table to graph $\begin{align*}y=x^3\end{align*}$ .
::让我们用表格来图y=x3 。

Draw a table and pick at least 5 values for $\begin{align*}x\end{align*}$ .
::为 x 绘制一张表格并至少选择 5 个值。

$\begin{align}x\end{align}$	$\begin{align}x^3\end{align}$	$\begin{align}y\end{align}$
-2	$\begin{align}(-2)^3\end{align}$	-8
-1	$\begin{align}(-1)^3\end{align}$	-1
0	$\begin{align}0^3\end{align}$	0
1	$\begin{align}1^3\end{align}$	1
2	$\begin{align}2^3\end{align}$	8

Plot the points and connect. This particular function is the parent graph for cubic functions. Recall from quadratic functions, that the parent graph has a leading coefficient of 1, no other $\begin{align*}x-\end{align*}$ terms , and no $\begin{align*}y-\end{align*}$ intercept . $\begin{align*}y=x^4\end{align*}$ and $\begin{align*}y=x^5\end{align*}$ are also parent graphs.
::绘制点和连接。此特定函数是立方函数的父图形。从二次函数中提醒注意, 父图形的系数为 1, 没有其他 x- terms, 没有 y=x4 和 y=x5 也是父图形。

Now, let's analyze the graph below. Find the critical values, end behavior, and find the domain and range .
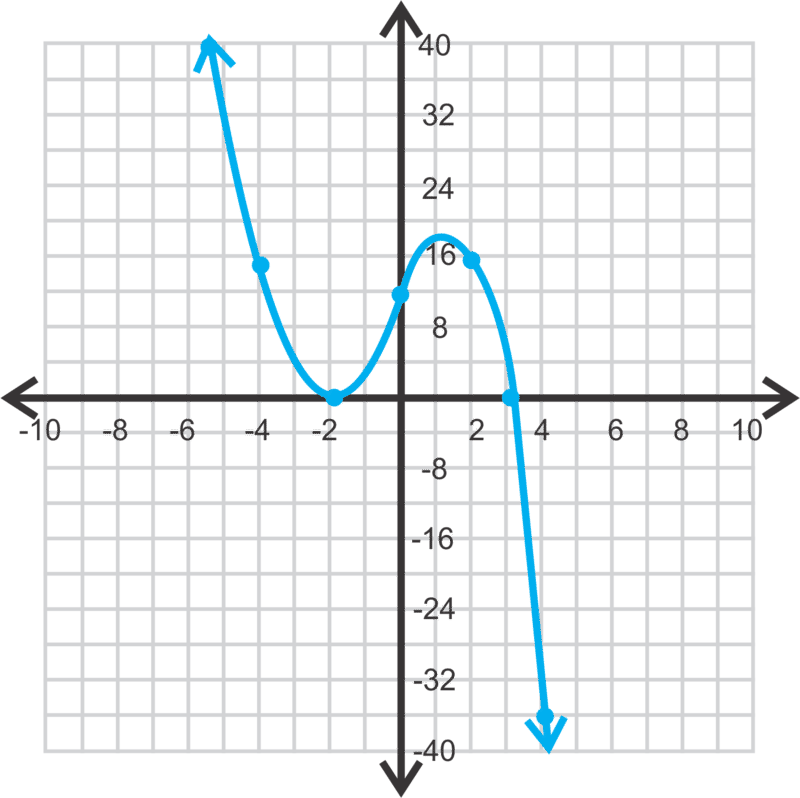
::现在,让我们分析下图。找到关键值, 结束行为, 并找到域和范围。

First, find the solutions. They appear to be (-2, 0), (1, 0), and (2, 0). Therefore , this function has a minimum degree of 3. However, look at the $\begin{align*}y-\end{align*}$ intercept. The graph slightly bends between the maximum and minimum. This movement in the graph tells us that there are two imaginary solutions (recall that imaginary solutions always come in pairs). Therefore, the function has a degree of 5. Approximate the other critical values:
::首先,找到解决方案。它们看起来是 (-2,0,0,1,0,2,0) 和 (2,0) 。因此,此函数的最小度为 3 。但是, 请看 y- interfect 。图表在最大值和最小值之间稍有弯曲。图中的这种移动告诉我们, 有两个假想解决方案( 提醒人们想象的解决方案总是双对产生 ) 。因此, 此函数的值为 5. 等同其他关键值 :

maximum: (-1.1, 10)
::最大值-1.1, 10)

minimum: (1.5, -1.3)
::最小值1.5, -1.3)

$\begin{align*}y-\end{align*}$ intercept: (0, 5)
::- 拦截: (0, 5)

In general, this function is mostly increasing and the ends go in opposite directions. The domain and range are both all real numbers.
::一般来说,这一功能主要在增加,最终方向相反。域和范围都是真实数字。

When describing critical values, you may approximate their location. You will later use the graphing calculator to find these values exactly.
::当描述关键值时,您可以大致估计其位置。以后您将使用图形计算器来精确查找这些值。

Sometime it can be tricky to see if a function has imaginary solutions from the graph. Compare the graph in the previous problem to the cubic function above it. Notice that it is smooth between the maximum and minimum. As was pointed out earlier, the graph from the previous problem bends. Any function with imaginary solutions will have a slightly irregular shape or bend like this one does.
::有时,看到一个函数是否从图形中存在假想的解决方案可能会很困难。比较上一个问题中的图形到上面的立方函数。注意它在最大和最小之间是顺畅的。如前所述, 先前问题的图会弯曲。任何带有假想解决方案的函数都会像这个函数那样有不规则的形状或弯曲。

Finally, let's sketch a graph of a function with roots $\begin{align*}-4, -3, \frac{1}{2}\end{align*}$ , and 3, has an absolute maximum at (2, 5), and has negative end behavior. This function does not have any imaginary roots.
::最后,让我们勾画一个函数的图示,该函数的根值为 - 4, 3, 3, 12, 3, 绝对最大值为 2, 5, 并且有负结束行为。此函数没有任何虚构的根。

There are several possible answers for this graph because we are only asking for a sketch. You would need more information to get an exact answer. Because this function has negative end behavior and four roots, we know that it will pass through the $\begin{align*}x-\end{align*}$ axis four times and face down. The absolute maximum is located between the roots $\begin{align*}\frac{1}{2}\end{align*}$ and 3. Plot these five points and connect to form a graph.
::此图表有几种可能的答案, 因为我们只要求草图。您需要更多信息才能得到准确的答案。由于此函数有负端行为和四个根, 我们知道它会通过 X - 轴 4 次, 面部会下降。绝对最大值位于根 12 和 3 之间。绘制这五个点并连接成图表。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the maximum height the coaster will reach over the domain [-1, 2].
::早些时候,有人要求你找到海岸车将到达的最大高度超过域 [ - - - 2] 。

Use a table to graph $\begin{align*}x^5 - 8x^3 + 10x + 6\end{align*}$ .
::使用图表表显示 x5- 8x3+10x+6。

Draw a table and pick at least 5 values for $\begin{align*}x\end{align*}$ . Remember that we are dealing only with x values between and including -1 and 2.
::为 x 绘制一张表格并至少选择 5 个值。记住, 我们只处理 X 值之间, 包括 - 1 和 2 之间的 x 值。请记住, 我们只处理 x 值。

$\begin{align}x\end{align}$	$\begin{align}y\end{align}$
-1	3
0	6
0.5	10.03125
1	9
2	-16

Plot the points and connect.
::绘制点和连接。

From your graph you can see that the maximum height the roller coaster reaches is just slightly over 10.
::从你的图表中可以看到云层滑雪车到达的最大高度略高于10度

Example 2
::例2

Use a table to graph $\begin{align*}f(x)=-(x+2)^2(x-3)\end{align*}$ .
::使用表格绘制 f(x) (x+2) 2(x)-3 。

This function is in intercept form . Because the factor , $\begin{align*}(x + 2)\end{align*}$ is squared, we know it is a repeated root. Therefore, the function should just touch at -2 and not pass through the $\begin{align*}x-\end{align*}$ axis. There is also a zero at 3. Because the function is negative, it will be generally decreasing. Think of the of the line between the two endpoints. It would be negative. Select several points around the zeros to see the behavior of the graph.
::此函数为截取形式。因为系数 (x+2) 是正方形, 我们知道它是一个重复的根。因此, 该函数应该只触摸 - 2, 而不是通过 x - 轴。 3 也有一个零, 因为函数是负的, 它一般会下降。想象两个端点之间的线。它会是负的。在零周围选择几个点来查看图形的行为。

$\begin{align}x\end{align}$	$\begin{align}y\end{align}$
-4	14
-2	0
0	12
2	16
3	0
4	-36

Example 3
::例3

Analyze the graph. Find all the critical values, domain, range and describe the end behavior.
::分析图表。查找所有关键值、域、区域并描述最终行为。

There are three real zeros at approximately -3.5, 1, and 7. Notice the curve between the zeros 1 and 7. This indicated there are two imaginary zeros, making this at least a fifth-degree polynomial. Think about an imaginary horizontal line at $\begin{align*}y = 3\end{align*}$ . This line would touch the graph five times, so there should be five solutions. Next, there is an absolute minimum at (-0.5, -7.5), a local maximum at (2.25, 5), a local minimum at (2.25, 2.25) and an absolute maximum at (5, 6). The $\begin{align*}y-\end{align*}$ intercept is at (0, -6). The domain and range are both all real numbers and the end behavior is mostly decreasing.
::大约 - 3. 5, 1 和 7. 注意 0 1 和 7 之间的曲线为 3 个实际零, 大约 - 3. 5, 1 和 7. 注意 0 1 和 7 之间的曲线, 显示有 2 个想象中的零, 使这至少有一个 5 度的多元度。考虑一个 y= 3 的想象中的水平线。这个线将触摸图形 5 次 , 所以应该有 5 个解决办法。其次, 绝对最低值 (-0.5, - 7.5 ) , 当地最高 2. 25 , 当地最低值 (2. 25, 2. 25 ) , 绝对最高值 ( 5 , 6 ) 。 y - intercept is 0, 6 。这个域和范围都是全部真实数字, 最终行为大多在减少。

Example 4
::例4

Draw a graph of the cubic function with solutions of -6 and a repeated root at 1. This function is generally increasing and has a maximum value of 9.
::绘制为 - 6 和 1 的重复根的立方函数图。此函数一般在增加, 最大值为 9 。

To say the function is “mostly increasing” means that the slope of the line that connects the two ends (arrows) is positive. Then, the function must pass through (-6, 0) and touch, but not pass through (1, 0). From this information, the maximum must occur between the two zeros and the minimum will be the double root .
::说此函数“ 大多增加 ” , 意指连接两个端( 箭头) 的线的斜坡是正的。然后, 函数必须经过( 6, 0) 和触摸, 而不是通过(1, 0 )。从此信息中, 最大值必须在两个零之间, 最小值将是双根。

Review
::回顾

Use the given $\begin{align*}x-\end{align*}$ values to make a table and graph the functions below.
::使用给定的 x - 值来绘制表格和图解下面的函数。

$\begin{aligned} f (x) & = x^{3} - 7 x^{2} + 15 x - 2 \\ x & = - 2, - 1, 0, 1, 2, 3, 4 \end{aligned}$
$\begin{align*}f(x) &= x^3-7x^2+15x-2\\ x &= -2, -1, 0, 1, 2, 3, 4\end{align*}$
::f(x) =x3 - 7x2+15x - 2x%2, - 1, 0, 1, 2, 3, 4

$\begin{aligned} g (x) & = - 2 x^{4} - 11 x^{3} - 3 x^{2} + 37 x + 35 \\ x & = - 5, - 4, - 3, - 2, - 1, 0, 1, 2 \end{aligned}$
$\begin{align*}g(x) &= -2x^4 - 11x^3 - 3x^2+37x+35\\ x &= -5, -4, -3, -2, -1, 0, 1, 2\end{align*}$
::g (x) 2x4 - 11x3 - 3x2+37x+35x%5 - 4, - 3, - 2, - 1, 0, 2

$\begin{aligned} y & = 2 x^{3} + 25 x^{2} + 100 x + 125 \\ x & = - 7, - 6, - 5, - 4, - 3, - 2, - 1, 0 \end{aligned}$
$\begin{align*}y &=2x^3+25x^2+100x+125\\ x &= -7,-6,-5,-4,-3,-2,-1,0\end{align*}$
::y=2x3+25x2+100x+125x=7,-6,-5,-4,-3,-2,-1,0

Make your own table and graph the following functions.
::以自己的表格和图表绘制下列函数。

$\begin{align*}f(x)=(x+5)(x+2)(x-1)\end{align*}$
:xx) = (x+5)(x+2)(x-1)

$\begin{align*}y=x^4\end{align*}$
::y=x4 y=x4

$\begin{align*}y=x^5\end{align*}$
::y=x5 y=x5

Analyze the graphs of $\begin{align*}y=x^2, y=x^3, y=x^4\end{align*}$ , and $\begin{align*}y=x^5\end{align*}$ . These are all parent functions. What do you think the graph of $\begin{align*}y=x^6\end{align*}$ and $\begin{align*}y=x^7\end{align*}$ will look like? What can you say about the end behavior of all even functions? Odd functions? What are the solutions to these functions?
::分析 y=x2, y=x3, y=x4 和 y=x5 的图形。这些都是父函数。您认为 y=x6 和 y=x7 的图形会是什么样子? 您对全部函数的结束行为能说什么? 奇数函数? 这些函数的解决方案是什么 ?

Writing How many repeated roots can one function have? Why?
::写入一个函数能有多少重复根? 为什么?

Analyze the graphs of the following functions. Find all critical values, the domain, range, and end behavior.
::分析以下函数的图形。查找所有关键值, 域、区域以及结束行为。

For questions 13-15, make a sketch of the following real-solution functions.
::对于问题13-15,请概述以下实际解决办法功能。

Draw two different graphs of a cubic function with zeros of -1, 1, and 4.5 and a minimum of -4.
::绘制两个不同的图表,以显示一立方函数的零点为-1、1、4.5和最少为-4。

A fourth-degree polynomial with roots of -3.2, -0.9, 1.2, and 8.7, positive end behavior, and a local minimum of -1.7.
::四度多球,根于-3.2、-0.9、1.2和8.7,正结束行为,当地最低为-1.7。

A fourth-degree function with solutions of -7, -4, 1, and 2, negative end behavior, and an absolute maximum at $\begin{align*}\left(-\frac{11}{2}, \frac{1755}{128}\right)\end{align*}$ .
::四度函数,溶液为-7、-4、1和2,负端行为,绝对上限为(-112、1755-128)。

Challenge Find the equation of the function from #15.
::挑战从 #15 找到函数的方程。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

$\begin{align}x\end{align}$	$\begin{align}x^3\end{align}$	$\begin{align}y\end{align}$
-2	$\begin{align}(-2)^3\end{align}$	-8
-1	$\begin{align}(-1)^3\end{align}$	-1
0	$\begin{align}0^3\end{align}$	0
1	$\begin{align}1^3\end{align}$	1
2	$\begin{align}2^3\end{align}$	8

Section outline

General

聚合函数图的查找和定义部分

Parts of a Polynomial Graph ::圆形图部分

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)