Course: 6.14 用图形计算计算器绘制多面函数图

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 用图形计算计算器绘制多面函数

Collapse Expand
用图形计算计算器绘制多面函数
To make a fair race between a dragster and a funny car, a scientist devised the following polynomial equation :
::为了在拖车和滑稽汽车之间公平竞争, 科学家设计了以下多元等式:

$\begin{align*}f(x) = 71.682x -60.427x^2 + 84.710x^3 -27.769x^4 + 4.296x^5 - 0.262x^6\end{align*}$ . What is the maximum point of this function's graph?
::f(x) = 71.682x- 60.427x2+84. 710x3- 27.769x4+4.296x5-0. 262.x6. 本函数图的最大点是什么?

Source: Rice University
::资料来源:水稻大学。

Graphing Polynomial Functions with a Calculator
::带有计算器的多圆函数图形

You have already used the graphing calculator to graph parabolas. Now, we will expand upon that knowledge and graph higher- degree . Then, we will use the graphing calculator to find the zeros , maximums and minimums.
::您已经使用图形计算器来绘制parabolas 。现在, 我们将扩展该知识并绘制更高度的图形。然后, 我们将使用图形计算器来找到零、最大值和最小值。

Let's graph $\begin{align*}f(x)=x^3+x^2-8x-8\end{align*}$ using a graphing calculator.
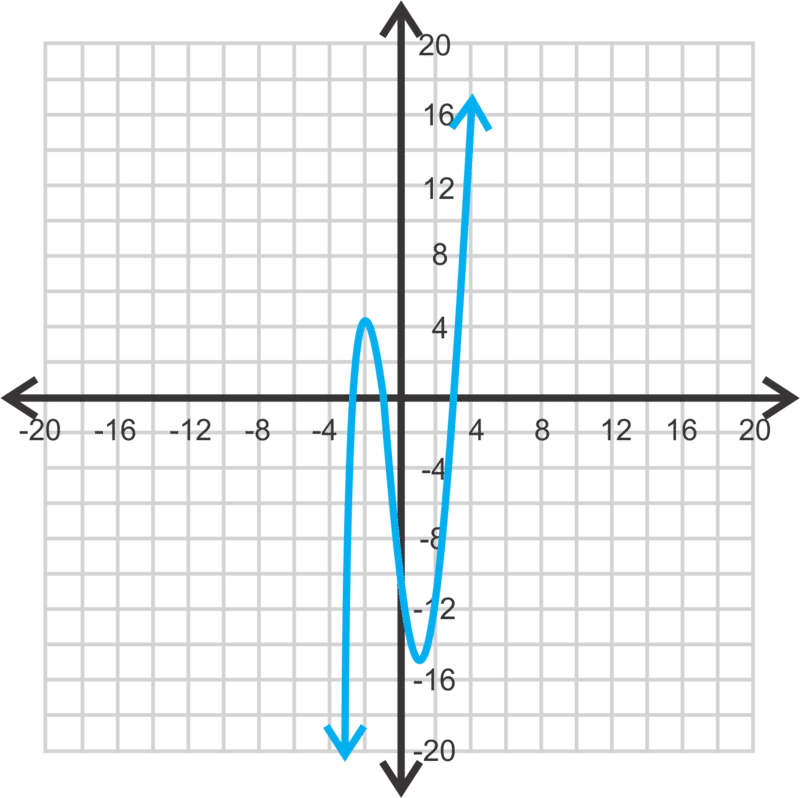
::让我们使用图形计算器来绘制图表f(x)=x3+x2-8x-8。

These instructions are for a TI-83 or 84. First, press $\begin{align*}Y=\end{align*}$ . If there are any functions in this window, clear them out by highlighting the = sign and pressing ENTER. Now, in $\begin{align*}Y1\end{align*}$ , enter in the polynomial. It should look like: $\begin{align*}x^\land 3+x^\land 2-8x-8\end{align*}$ . Press GRAPH .
::这些指令用于 TI- 83 或 84. 首先, 按 Y = 。如果此窗口中有任何函数, 请通过突出 = 符号和按 ENTER 来清除它们。现在, 在 Y1 中, 请在多义中输入。它应该像 : x+3+x% 2 - 8x-8 -8 。请按 GRAPH 键。

To adjust the window, press ZOOM . To get the typical -10 to 10 screen (for both axes), press 6:ZStandard. To zoom out, press ZOOM, 3:ZoomOut, ENTER, ENTER. For this particular function , the window needs to go from -15 to 15 for both $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ . To manually input the window, press WINDOW and change the $\begin{align*}Xmin, Xmax, Ymin,\end{align*}$ and $\begin{align*}Ymax\end{align*}$ so that you can see the zeros, minimum and maximum. Your graph should look like the one above.
::要调整窗口, 请按 ZOOM 。要获得典型的 - 10 到 10 屏幕( 两轴) , 按 6: ZStandard 。要放大, 请按 ZOOM 、 3: 缩小、 ENTER、 ENTER 。对于此特定函数, x 和 y , 窗口需要从 - 15 到 15 。要手动输入窗口, 请按 WINDOW 键, 并更改 Xmin、 Xmax、 Ymin 和 Ymax, 以便您可以看到零, 最小和最大值。您的图表应该像上面的图表一样。

Now, let's find the zeros, maximum, and minimum of the function from the previous problem above.
::现在,让我们从上一个问题中找到零、最大和最小的函数。

To find the zeros, press $\begin{align*}2^{nd}\end{align*}$ TRACE to get the CALC menu. Select 2:Zero and you will be asked “Left Bound?” by the calculator. Move the cursor (by pressing the $\begin{align*}\uparrow\end{align*}$ or $\begin{align*}\downarrow\end{align*}$ ) so that it is just to the left of one zero. Press ENTER. Then, it will ask “Right Bound?” Move the cursor just to the right of that zero. Press ENTER. The calculator will then ask “Guess?” At this point, you can enter in what you think the zero is and press ENTER again. Then the calculator will give you the exact zero. For the graph from the previous problem above, you will need to repeat this three times. The zeros are -2.83, -1, and 2.83.
::要找到零点, 请按第二次 TRACE 来获取 CALC 菜单。选择 2: 零和您将会被计算器“ 左转 ” 。请将光标移动( 按或 ) , 以便仅向左一点。按 ENTER 。然后, 它会询问 “ 右转 ” ? 。 ” 将光标移到零点右转。按 ENTER 。此时, 您可以输入您认为的零点, 然后再按 ENTER 键。然后, 计算器会给出准确的零。对于上面问题的图表, 您需要重复三次。零是 - 2. 83、 - 1 和 2. 83 。

To find the minimum and maximum, the process is almost identical to finding zeros. Instead of selecting 2:Zero , select 3:min or 4:max . The minimum is (1.33, -14.52) and the maximum is (-2, 4).
::要找到最小值和最大值,该过程几乎与找到零几乎完全相同。而不是选择 2:0,选择 3:min 或 4:max 。最小值为 1.33, - 14.52, 最大值为 2, 4。

Finally, let's find the $\begin{align*}y-\end{align*}$ intercept of the graph from the same problem above.
::最后,让我们从上面同样的问题找到图表的 Y - 截取点。

If you decide not to use the calculator, plug in zero for $\begin{align*}x\end{align*}$ and solve for $\begin{align*}y\end{align*}$ .
::如果您决定不使用计算器, x 的插入为零, y 的解答为。

$\begin{aligned} f (0) & = 0^{3} + 0^{2} - 8 \cdot 0 - 8 \\ = - 8 \end{aligned}$
$\begin{align*}f(0) &= 0^3+0^2 - 8 \cdot 0 - 8\\ &= -8\end{align*}$
::f( 0) = 03+02-8_8_0-88

Using the graphing calculator, press $\begin{align*}2^{nd}\end{align*}$ TRACE to get the CALC menu. Select 1:value. $\begin{align*}X=\end{align*}$ shows up at the bottom of the screen. If there is a value there, press CLEAR to remove it. Then press 0 and ENTER. The calculator should then say “ $\begin{align*}Y=-8\end{align*}$ .”
::使用图形计算器, 按 2ndTRACE 来获取 CALC 菜单。选择 1: value. X = 显示在屏幕底部。如果有数值, 请按 CLEAR 来删除它。然后按 0 和 ENTER 键。计算器应该说“ Y 8 ” 。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the maximum point of the function's graph.
::早些时候,您被要求找到函数图的最大点。

If you plug the equation $\begin{align*}f(x) = 71.682x -60.427x^2 + 84.710x^3 -27.769x^4 + 4.296x^5 - 0.262x^6\end{align*}$ into your calculator, you find that the maximum occurs when $\begin{align*}x = 6.15105\end{align*}$ . At that value of x , f(x) equals 1754.43. Therefore the maximum point of the function's graph is (6.15105, 1754.43).
::如果您在计算器中插入方程式 f(x) = 71.682x- 60.427x2+84. 710x3- 27.769x4+4.296x5-0. 262x6,您就会发现最大值出现在 x= 6.15105 时。在此值x, f(x) 等于 1754.43。因此函数图形的最大值是 (6.15105, 1754.43 ) 。

Example 2
::例2

Graph and find the critical values: $\begin{align*}f(x)=-\frac{1}{3}x^4-x^3+10x^2+25x-4\end{align*}$
::图形并查找关键值: f( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\4\\\\\\\\\\\\\\\\\\\\\4\4\\\\\4\\\\\\\\\\\\\\\\\4

zeros: -5.874, -2.56, 0.151, 5.283
::零: -5.874,-2.56, 0.151, 5.283

$\begin{align*}y-\end{align*}$ intercept: (0, -4)
::- 拦截: (0, 4)

minimum: (-1.15, -18.59)
::最小值-1.15, - 18.59)

local maximum: (-4.62, 40.69)
::当地最大-4.62, 40.69)

absolute maximum: (3.52, 113.12)
::绝对上限3.52, 113.12)

Example 3
::例3

Graph and find the critical values: $\begin{align*}g(x)=2x^5-x^4+6x^3+18x^2-3x-8\end{align*}$
::图形并查找关键值: g(x)=2x5-x4+6x3+18x2-3x-8

zeros: -1.413, -0.682, 0.672
::零: -1.413,-0.682,0.672

$\begin{align*}y-\end{align*}$ intercept: (0, -8)
::- 拦截: (0, - 8)

minimum: (-1.11, 4.41)
::最低-1.11, 4.41)

maximum: (0.08, -8.12)
::最大值0.08, - 8.12)

Example 4
::例4

Find the domain and range of $\begin{align*}f(x)=-\frac{1}{3}x^4-x^3+10x^2+25x-4\end{align*}$ and $\begin{align*}g(x)=2x^5-x^4+6x^3+18x^2-3x-8.\end{align*}$
::查找 f( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\x5x5x5x5\x5xxx -\\\\\\\x5x -\\\\x5x -\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\x\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

The domain of $\begin{align*}f(x)\end{align*}$ is all real numbers and the range is all real numbers less than the maximum; $\begin{align*}(-\infty, 113.12]\end{align*}$ . The domain and range of $\begin{align*}g(x)\end{align*}$ are all real numbers.
::f( x) 域是全部真实数字, 范围是全部实际数字, 而所有实际数字都低于最大数字 (,113.12)] 。 g( x) 的域和范围是全部真实数字。

Review
::回顾

Graph questions 1-6 on your graphing calculator. Sketch the graph in an appropriate window. Then, find all the critical values, domain, range, and describe the end behavior.
::图形计算器上的图解问题 1 - 6 。在适当的窗口中将图纸拖动。然后, 查找所有关键值、域、范围, 并描述最终行为。

$\begin{align*}f(x)=2x^3+5x^2-4x-12\end{align*}$
:x) = 2x3+5x2-4x- 12

$\begin{align*}h(x)=-\frac{1}{4}x^4-2x^3-\frac{13}{4} x^2-8x-9\end{align*}$
::h (x) 14x4 - 2x3 - 134x2 - 8x- 9

$\begin{align*}y=x^3-8\end{align*}$
::y=x3 - 8 y=x3 - 8

$\begin{align*}g(x)=-x^3-11x^2-14x+10\end{align*}$
::g (x) x3- 11x2- 14x+10

$\begin{align*}f(x)=2x^4+3x^3-26x^2-3x+54\end{align*}$
:x) = 2x4+3x3-26x2 -3x+54

$\begin{align*}y=x^4+2x^3-5x^2-12x-6\end{align*}$
::y=x4+2x3 - 5x2 - 12x- 6

What are the types of solutions in #2?
::#2的解决方案是什么类型?

Find the two imaginary solutions in #3.
::在3号中找到两个假想的解决方案。

Find the exact values of the irrational roots in #5.
::找出5中不合理根的准确值。

Determine if the following statements are SOMETIMES, ALWAYS, or NEVER true. Explain your reasoning.
::确定以下声明是时空声明, ALWAYS, 还是永远不真实。请解释一下您的推理。

The range of an even function is $\begin{align*}(-\infty, max]\end{align*}$ , where max is the maximum of the function.
::一个偶数函数的范围是 (, 最大值), 最大值是函数的最大值。

The domain and range of all odd functions are all real numbers.
::所有奇数函数的域和范围都是真实数字。

A function can have exactly three imaginary solutions.
::函数可以完全有三个假想的解决方案。

An $\begin{align*}n^{th}\end{align*}$ degree polynomial has $\begin{align*}n\end{align*}$ real solutions.
::Nnth 度多面性具有真正的解决方案。

The parent graph of any polynomial function has one zero.
::任何多边函数的母形图为 0。

Challenge The exact value for one of the zeros in #2 is $\begin{align*}-4+\sqrt{7}\end{align*}$ . What is the exact value of the other root? Then, use this information to find the imaginary roots.
::挑战 # 2 中的零的准确值是 4+7 。另一个根的准确值是多少 ? 然后, 使用此信息来找到假想的根。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

用图形计算计算器绘制多面函数

Graphing Polynomial Functions with a Calculator ::带有计算器的多圆函数图形

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Graphing Polynomial Functions with a Calculator
::带有计算器的多圆函数图形

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)