Course: 7.4 平方根函数图

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

图形平方根函数

Mrs. Garcia has assigned her student the function $\begin{aligned} y = - \sqrt{x + 2} - 3 \end{aligned}$ to graph for homework. The next day, she asks her students which quadrant(s) their graph is in.
::Garcia夫人指派她的学生用yx+2-3功能来图表做家庭作业,第二天,她问她的学生他们的图表在哪个象限里。

Alendro says that because it is a square root function , it can only have positive values and therefore his graph is only in the first quadrant .
::Alendro说,因为它是一个平方根函数,它只能有正值,因此他的图表只在第一个象限内。

Dako says that because of the two negative sign, all y values will be positive and therefore his graph is in the first and second quadrants .
::Dako说,由于两个负的信号,y的所有值都将是正值,因此他的图表在第一和第二四位数中。

Marisha says they are both wrong. Because it is a negative square root function, her graph is in the third and fourth quadrants.
::Marisha说两者都是错的。因为这是一个负平方根函数, 她的图表在第三和第四个四分位数中。

Which one of them is correct?
::哪一个是正确的?

Graphing Square Root Functions
::图形平方根函数

A square root function has the form $\begin{aligned} y = a \sqrt{x - h} + k \end{aligned}$ , where $\begin{aligned} y = \sqrt{x} \end{aligned}$ is the parent graph . Graphing the parent graph, we have:
::平方根函数有 y=ax-h+k 的窗体, Y=x 是母图。

x	y
16	4
9	3
4	2
1	1
0	0
-1	und

Notice that this shape is half of a parabola , lying on its side. For $\begin{aligned} y = \sqrt{x} \end{aligned}$ , the output is the same as the input of $\begin{aligned} y = x^{2} \end{aligned}$ . The domain and range of $\begin{aligned} y = \sqrt{x} \end{aligned}$ are all positive real numbers, including zero. $\begin{aligned} x \end{aligned}$ cannot be negative because you cannot take the square root of a negative number.
::请注意, 此形状是 parbola 的半。对于 y=x , 输出与 y=x 的输入相同。 y=x 的域和范围都是正数, 包括 0。 x 不能是负数, 因为不能从负数的平方根中取出正数。

Let's graph $\begin{aligned} y = \sqrt{x - 2} + 5 \end{aligned}$ without a calculator.
::让我们用图y=x-2+5来显示无计算器的 y=x-2+5 。

To graph this function, draw a table. $\begin{aligned} x = 2 \end{aligned}$ is a critical value because it makes the radical zero.
::要绘制此函数,请绘制表格。 x=2 是一个关键值,因为它使基数为零。

x	y
2	5
3	6
6	7
11	8

After plotting the points, we see that the shape is exactly the same as the parent graph. It is just shifted up 5 and to the right 2. Therefore, we can conclude that $\begin{aligned} h \end{aligned}$ is the horizontal shift and $\begin{aligned} k \end{aligned}$ is the vertical shift .
::在绘制了点后, 我们可以看到形状与父图完全相同。它只是向上移了 5 和向右移了 2 。因此, 我们可以得出结论, h 是水平转换, k 是垂直转换。

The domain is all real numbers such that $\begin{aligned} x \geq 2 \end{aligned}$ and the range is all real numbers such that $\begin{aligned} y \geq 5 \end{aligned}$ .
::域名是所有真实数字, 即 x% 2, 范围是所有真实数字, 即 y% 5 。

Now's let's graph $\begin{aligned} y = 3 \sqrt{x + 1} \end{aligned}$ and find the domain and range.
::现在让我们来绘制 y=3x+1 并找到域和范围。

From the previous problem , we already know that there is going to be a horizontal shift to the left one unit. The 3 in front of the radical changes the width of the function. Let’s make a table.
::从上一个问题开始,我们已经知道左侧的单位会横向移动。 3 前面的3 改变函数的宽度。让我们来做一张表格。

x	y
$\begin{aligned} - 1 \end{aligned}$	0
0	3
3	6
8	9
15	12

Notice that this graph grows much faster than the parent graph. Extracting $\begin{aligned} (h, k) \end{aligned}$ from the equation , the starting point is $\begin{aligned} (- 1, 0) \end{aligned}$ and then rather than increase at a “slope” of 1, it is three times larger than that.
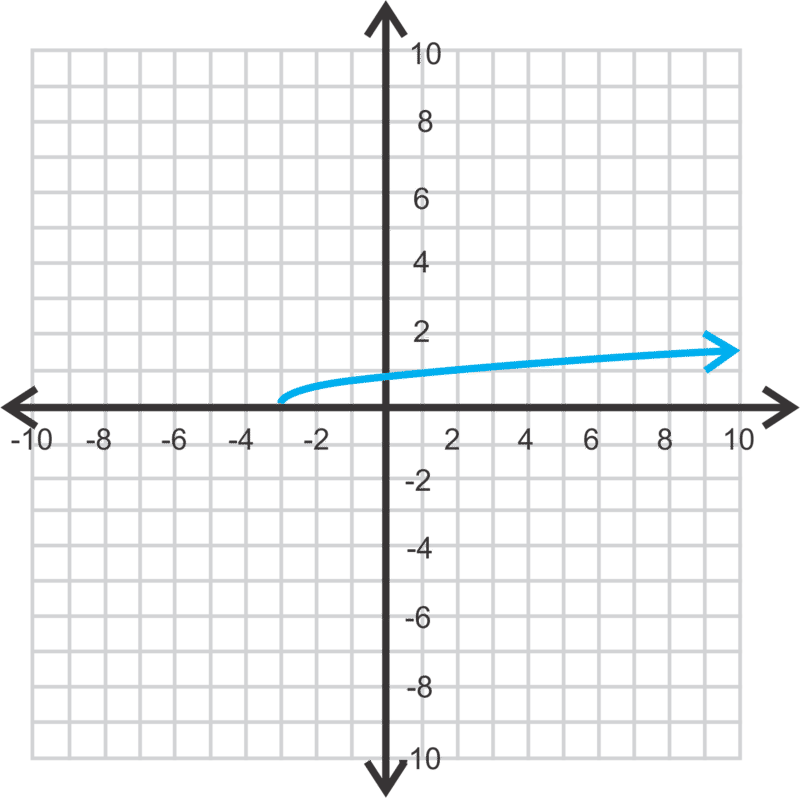
::请注意, 此图的生长速度比父图快得多。从方程式中提取( h, k) 时, 起始点是 (- 1, 0) , 而不是在 1 的“ 斜面” 上增加, 它比该方程式大三倍。

Finally, let's graph $\begin{aligned} f (x) = - \sqrt{x - 2} + 3 \end{aligned}$ .
::最后,让我们用图表f(x)x-2+3。

Extracting $\begin{aligned} (h, k) \end{aligned}$ from the equation, we find that the starting point is $\begin{aligned} (2, 3) \end{aligned}$ . The negative sign in front of the radical indicates a reflection . Let’s make a table. Because the starting point is $\begin{aligned} (2, 3) \end{aligned}$ , we should only pick $\begin{aligned} x \end{aligned}$ -values after $\begin{aligned} x = 2 \end{aligned}$ .
::从方程中提取 (h,k) 时, 我们发现起点是(2, 3) 。激进分子前面的负符号表示反射。让我们来做一张表。因为起点是(2, 3 ) , 我们只能在 x=2 之后选择 x 值。

x	y
2	3
3	2
6	1
11	0
18	-1

The negative sign in front of the radical, we now see, results in a reflection over $\begin{aligned} x \end{aligned}$ -axis.
::现在我们看到,激进分子面前的负面迹象导致X轴反射。

Using the graphing calculator: If you wanted to graph this function using the TI-83 or 84, press $\begin{aligned} Y = \end{aligned}$ and clear out any functions. Then, press the negative sign, (-) and 2nd $\begin{aligned} x^{2} \end{aligned}$ , which is $\begin{aligned} \sqrt{} \end{aligned}$ . Then, type in the rest of the function, so that $\begin{aligned} Y = - \sqrt{} (X - 2) + 3 \end{aligned}$ . Press GRAPH and adjust the window.
::使用图形计算器 : 如果您想要使用 TI- 83 或 84 来图形显示此函数, 请按 Y = 并清除任何函数。然后按负符号 (-) 和 2ndx2 , 即。然后键入此函数的其余部分, 以便 Y (X-2) +3. 按 GRAPH 键并调整窗口。

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine which student was correct.
::早些时候,有人要求你确定哪个学生是正确的。

If you graph the function $\begin{aligned} y = - \sqrt{x + 2} - 3 \end{aligned}$ , you will see that its domain is $\begin{aligned} x \geq - 2 \end{aligned}$ , which makes all of the quadrants possibilities. But its range is $\begin{aligned} y \leq - 3 \end{aligned}$ , limiting the graph to the third and fourth quadrants. Therefore, Marisha is correct.
::如果您将函数 yx+2- 3 图形, 您就会看到它的域是 x2, 这使得所有四重体都有可能。但范围是 y3 , 将图限制在第三和第四夸体。因此, Marisha 是正确的。

Example 2
::例2

Evaluate $\begin{aligned} y = - 2 \sqrt{x - 5} + 8 \end{aligned}$ when $\begin{aligned} x = 9 \end{aligned}$ .
::当 x=9 时评价 y2x- 5+8 。

Plug in $\begin{aligned} x = 9 \end{aligned}$ into the equation and solve for $\begin{aligned} y \end{aligned}$ .
::将 x=9 中的插件插在公式和y 的解析中。

$\begin{aligned} y = - 2 \sqrt{9 - 5} + 8 = - 2 \sqrt{4} + 8 = - 2 (2) + 8 = - 4 + 8 = - 4 \end{aligned}$
::y 29 - 5+8 _ 24+8 _ 2 (2)+8 _ 4+8 _ 4

Example 3
::例3

Graph, describe the relationship to the parent graph and find the domain and range: $\begin{aligned} y = \sqrt{- x} \end{aligned}$ .
::图表,描述与父图形的关系,并查找域和范围:yx。

Here, the negative is under the radical. This graph is a reflection of the parent graph over the $\begin{aligned} y \end{aligned}$ -axis.
::这里的负值在基下。这个图是 Y 轴上的母图的反射。

The domain is all real numbers less than or equal to zero. The range is all real numbers greater than or equal to zero.
::域名是所有实际数字小于或等于零。范围是所有实际数字大于或等于零。

Example 4
::例4

Graph, describe the relationship to the parent graph and find the domain and range: $\begin{aligned} f (x) = \frac{1}{2} \sqrt{x + 3} \end{aligned}$ .
::图表,描述与父图形的关系,并查找域和范围:f(x)=12x+3。

The starting point of this function is $\begin{aligned} (- 3, 0) \end{aligned}$ and it is going to “grow” half as fast as the parent graph.
::此函数的起点是 (- 3,0) , 它的“ 增长” 速度会快于母图的一半。

The domain is all real numbers greater than or equal to -3. The range is all real numbers greater than or equal to zero.
::域是所有实际数字大于或等于-3.。范围是所有实际数字大于或等于0。

Example 5
::例5

Graph using a graphing calculator $\begin{aligned} f (x) = - 4 \sqrt{x - 5} + 1 \end{aligned}$ .
::使用图形计算器 f( x)\\% 4x- 5+1 的图形图。

Using the graphing calculator, the function should be typed in as: $\begin{aligned} Y = - 4 \sqrt{} (X - 5) + 1 \end{aligned}$ . It will be a reflection over the $\begin{aligned} x \end{aligned}$ -axis, have a starting point of $\begin{aligned} (5, 1) \end{aligned}$ and grow four times as fast as the parent graph.
::使用图形计算计算器,函数应输入为:Y4(X-5)+1。它将是X轴的反射,起点为(5,1),生长速度为父图形的四倍。

Review
::回顾

Evaluate the function, $\begin{aligned} f (x) = - \sqrt{x - 4} + 3 \end{aligned}$ for the following values of x .
::对以下 x 值的 f(x) x-4+3 函数进行评价。

$\begin{aligned} f (3) \end{aligned}$
::f(3) f(3)

$\begin{aligned} f (6) \end{aligned}$
::f(6) f(6)

$\begin{aligned} f (13) \end{aligned}$
::f(13)

What is the domain of this function?
::此函数的域是什么 ?

Graph the following square root functions and find the domain and range. Use your calculator to check your answers.
::绘制以下平方根函数图并找到域和范围。使用您的计算器来检查答案。

$\begin{aligned} f (x) = \sqrt{x + 2} \end{aligned}$
:xx)=x+2

$\begin{aligned} y = \sqrt{x - 5} - 2 \end{aligned}$
::y=x - 5-2

$\begin{aligned} y = - 2 \sqrt{x + 1} \end{aligned}$
::y2x+1

$\begin{aligned} f (x) = 1 + \sqrt{x - 3} \end{aligned}$
:xx)=1+x-3)

$\begin{aligned} f (x) = \frac{1}{2} \sqrt{x + 8} \end{aligned}$
:xx)=12x+8

$\begin{aligned} f (x) = 3 \sqrt{x + 6} \end{aligned}$
:xx)=3x+6)

$\begin{aligned} y = 2 \sqrt{1 - x} \end{aligned}$
::y=21-x y=21-x

$\begin{aligned} y = \sqrt{x + 3} - 5 \end{aligned}$
::y=x+3 - 5 y=x+3 - 5

$\begin{aligned} f (x) = 4 \sqrt{x + 9} - 8 \end{aligned}$
:xx)=4x+9-8

$\begin{aligned} y = - \frac{3}{2} \sqrt{x - 3} + 6 \end{aligned}$
::y32x-3+6

$\begin{aligned} y = - 3 \sqrt{5 - x} + 7 \end{aligned}$
::y35 - x+7 y35 - x+7

$\begin{aligned} f (x) = 2 \sqrt{3 - x} - 9 \end{aligned}$
:xx)=23-x-9)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

图形平方根函数

Graphing Square Root Functions ::图形平方根函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)