1.17 线形和赤道模型
章节大纲
-
Learning to express real-life situations as mathematical functions allows seemingly complex ideas and actions to be broken down into smaller, simpler parts and analyzed.
::学习以数学功能来表达现实生活状况,这样就可以将看起来复杂的思想和行动细分为更小、更简单的部分并加以分析。How might you express the following mathematically?
::你如何用数学表达以下内容?Two brothers decide to race home from school, taking different routes. The second brother leaves 5 minutes after the first, and both arrive at home at the same time.
::第二兄弟在第一次离家5分钟后离开,两人同时回家。Linear and Quadratic Models
::线性模型和二次曲线模型Linear Models
::线性模型The simplest functions are generally linear models. For instance, the equation y = 3 x could be used to represent how much money you would bring in if you sold x boxes of cookies for $3 per box. Many situations can be modeled with . The key idea is that some quantity in the situation has a constant rate of change . In the cookie-selling example, every box costs $3.00. Therefore the profits increase at a constant rate . In sum, linear functions are used to model a situation of constant change, either increase or decrease.
::最简单的函数一般都是线性模型。 例如, 等式y = 3x 可以用来表示如果每箱卖掉 x 盒饼干, 每箱3美元, 你将带来多少钱。 许多情况下都可以建模。 关键的想法是, 某些数量在情况中具有恒定的变动率。 在饼干销售中, 每个框都要花费3.00美元。 因此利润会以恒定的速率增长。 总之, 线性函数用来模拟一个不断变化的情况, 不管是增还是减。Quadratic Models
::二次曲线模型Quadratic functions may also be used as models. For example, the function could be used to represent the area of a rectangular plot of land enclosed on three sides by 100 feet of fence. This model could be used to identify the maximum possible area for the plot of land.
::二次曲线函数也可以作为模型使用。例如,函数A(x)=50x-x22可以用来代表三边以100英尺围栏封闭的长方形土地块面积。这个模型可以用来确定土地块的最大可能面积。Another example is a situation in which a ball is tossed into the air. The ball will travel up, and then it will travel down until it hits the ground. How high will the ball go? When will it reach the ground? This kind of situation can be modeled by a function of the form h ( t ) = -16 t 2 + v 0 t + h 0 . The variable t represents the time since the ball was thrown. The coefficient v 0 represents the initial velocity of the ball, and the constant h 0 represents the initial height of the ball. The constant -16 comes from the force of gravity which pulls the ball down, which is why it is negative. Example 3 shows a specific situation of this form.
::另一个例子是球被抛入空气中的情况。 球会向上移动, 然后向下移动, 直到击中地面。 球会升到多高 。 球会升到多高 ? 它何时会到达地面 ? 这种情况可以通过表h( t) = - 16t2 + - v0t + h0 的函数模拟。 变量t 代表球投出后的时间 。 系数 v0 代表球的初始速度, 而恒值 h0 代表球的初始高度 。 恒值 - 16 来自于将球拉倒的引力, 这就是为什么它是负的。 例3 显示了这种形式的特定情况 。Examples
::实例Example 1
::例1Earlier, you were asked to come up with a mathematical model for the following statement.
::早些时候,你被要求想出一个数学模型 来做以下陈述。Two brothers decide to race home from school, taking different routes. The second brother leaves 5 minutes after the first, and both arrive at home at the same time.
::第二兄弟在第一次离家5分钟后离开,两人同时回家。There are a number of different ways to model the information, depending on what part(s) of the information you choose to use. A couple of examples include:
::根据您选择使用的信息的哪一部分,有多种不同的信息模式。If t = the time the second brother took to get home, then t + 5 = the time the first brother took.
::如果t=第二兄弟回家的时间,那么t+5=第一兄弟回家的时间。If t = the time the first brother took to get home, then (t + (t - 5))/2 represents the average time to run home.
::如果t = 第一兄弟回家的时间,那么(t+ (t-5))/2 表示平均回家时间。Your model may be similar, or may be written differently, but should compare different values given in the story problem.
::您的模型可能是相似的, 也可能是不同的写法, 但应该比较故事问题中给出的不同值 。Example 2
::例2You run a lawn mowing business, and charge $15 per lawn. Write a linear function to describe the amount of money made as a function of the number of lawns mowed.
::您经营草坪修剪业务, 每草坪收费$15 。 写一个线性函数, 描述根据修剪草坪数量计算的货币金额 。If you express the number of lawns mowed as l , then $15 multiplied by l would represent the total money made based on the number of lawns, therefore:
::如果你将草坪数目改成l, 15美元乘1美元, 代表根据草坪数目所赚的总金额, 因此:total income = 15* l
::总收入=15*1Example 3
::例3You drop a rock off the edge of a cliff, and time the fall in seconds. Determine the function that models the height of the cliff as a function of falling time in seconds.
::您将一块岩石从悬崖边缘扔下, 并将倒塌时间以秒计。 确定以秒计落时间函数来模拟悬崖高度的函数 。With an initial velocity of 0, the height of the cliff may be calculated with the formula : h ( t ) = 16 t 2 .
::最初速度为0,可按公式:h(t)=16t2计算悬崖的高度。Example 4
::例4You are standing on the roof of a building that is 20 feet above the ground. You toss a ball into the air with an initial vertical velocity of 40 ft/sec, so that it will land on the ground, not on the roof. How high will the ball go, and when will it reach its maximum height? When will the ball hit the ground?
::你站在地上20英尺高的建筑物的屋顶上。你将一颗球投向空中,最初垂直速度为40英尺/秒,以便它降落在地面上,而不是在屋顶上。球会有多高,什么时候会达到最高高度?球什么时候会击中地面?First we need to write a function to model the situation. Using the general form of the equation given above, we can write the function h ( t ) = -16 t 2 + 40 t + 20 , where h ( t ) represents the height above the ground.
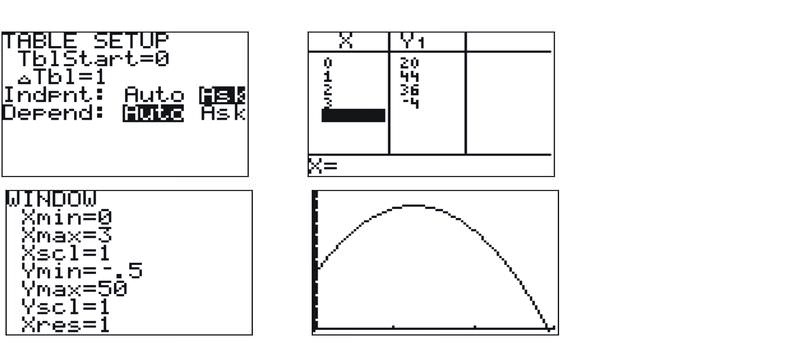
::首先,我们需要写入一个函数来模拟情况。使用上面给定的方程式的一般形式, 我们可以写入函数 h( t) = - 16t2 + 40t + 20, 其中 h( t) 代表地面的高度 。To answer the first question, we need to examine the graph of the function. If you graph this equation on your calculator, you will need to determine a good viewing window. One way to start to determine a good window is to take into account the y - intercept of the function. In this case, the y -intercept is (0, 20). Think about what kind of function this is: a parabola , facing downwards. This fact should lead you to think that we need to look at y -values well above 20 . It is often useful to look at a table of values. Using the “ask” capability of the calculator, if you input x values of 1, 2, and 3, you will see that the function goes up to 44 at x = 1. The maximum value is most likely somewhere near x = 1. Press WINDOW, and set xmin = 0, xmax = 3. Then set Ymin = 0 (or a little less, if you want to see the y -axis). Ymax should be no less than 44, though you may want to make it larger, such as 50 or more, just to be sure that you can see the vertex . Once you have set the window, press GRAPH.
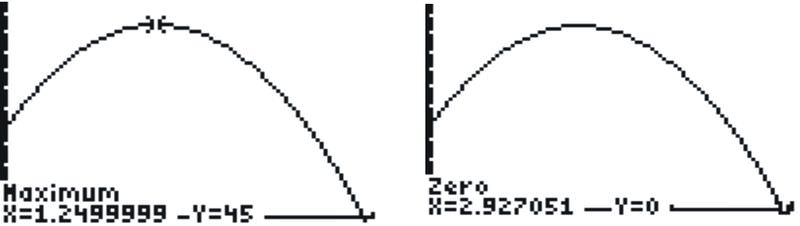
::要回答第一个问题, 我们需要检查函数的图形 。 如果您在计算器上绘制这个公式, 您需要确定一个良好的查看窗口 。 开始确定一个好的窗口的一个方法就是考虑函数的 Y 界面。 在此情况下, y 接口是 ( 0, 20) 。 考虑一下这个功能的种类: 向下方向的 抛光镜。 这一事实应该导致您认为我们需要看 y 值 20 上方的 Y 值 。 如果您输入 x 1, 2 和 3 的计算器的“ ask ” 功能, 您需要确定一个良好的查看窗口 。 如果您输入 x 的 x 值为 1 , 您将看到该函数的“ ask ” 功能在 x = 1 。 在此情况下, y 界面的最大值最有可能在 x = 1. 按WINOW, 并设置 xmin = 0, xmax = 3 。 然后设定 Ymin = 0 (或者稍小一点, 如果您想要看到 y- 轴的话) , 通常有用 查看一个数值表 。 Y 。 您可以将 Y 降为 44 。 您可以使它变大一些 。Now you should see the parabola. To identify the coordinates of the vertex, you can use the MAX function in the CALC menu. Remember that the calculator will ask you to input a left bound, a right bound, and a guess for the maximum. If you use the MAX function, you should find that the coordinates of the vertex are (1.25, 45). This means that 1.25 seconds after the ball is thrown into the air, it reaches a maximum height of 45 feet.
::现在您应该看到抛物线。 要确定顶点的坐标, 您可以在 CALC 菜单中使用 MAX 函数 。 记住计算器会要求您输入左键、 右键和最大值的猜测。 如果您使用 MAX 函数, 您应该发现顶点的坐标是 1. 25, 45 。 这意味着在球被投入空气后1. 25 秒, 最大高度为 45 英尺 。Now, to answer the second part of the question, we need to determine when the height of the ball is 0. Graphically, we are looking for the x -intercept of the parabola. If you return to the GRAPH screen, you should see that the x -intercept is around 3. If we want to determine the exact value, or at least a good approximation of the x -intercept, we can use the ZERO function. Press 2 nd TRACE to get the CALC menu, and choose option 2, ZERO. Like the MAX function, you need to input a left bound, a right bound, and a guess, although the guess is optional – just press ENTER. (Note that the calculator works this way because it is asking you to identify which x -intercept to calculate. The parabola has two x- intercepts , and other functions may have more.) Using the ZERO function, you should find that the x -intercept is approximately 2.93. This means that the ball reaches the ground in just under 3 seconds.
::现在,为了回答问题的第二部分,我们需要确定球的高度是0。 图形化地说, 我们是在寻找抛光线的 X inter 。 如果您返回 GRAPH 屏幕, 您应该看到 X inter 是在 3 周围 。 如果我们想要确定确切值, 或者至少是 x inter 的一个很好的近似值, 我们可以使用 ZERO 函数 。 按 第二次 TRACE 来获取 CALC 菜单, 并选择 选项 2 , ZERO 。 和 MAX 函数一样, 您需要输入一个左键、 右键和猜想, 尽管猜测是可选的 — 只需按 ENTER 。 (注意, 计算器可以这样工作, 因为它要求您确定要计算哪个 x inter 。 parbola 有两个 X 界面, 和其他函数可能更多 。) 使用 ZERO 函数, 您应该发现 x inter 大约是 2. 93 。 这意味着球在 3 秒内到达地面 。Example 5
::例5The Arlington Freshmen class wants to have a fundraiser. The class wants to buy a number of $4.00 flip-flops and $5.00 baseball hats, and has a total of $100 to spend.
::阿林顿新人班想要一个筹款活动。该班想买几个四块的翻滚鞋和五块的棒球帽,总共要花100美元。To express this information as a function, remember that the question specified that there was $100 to spend, and that any money not spent on hats (at $5 ea) was spent on flip-flops (at $4 ea).
::为了将这一信息作为一种功能来表达,请记住,问题明确指出,有100美元需要支出,任何未花在帽子上的钱(5美元ea)都花在翻转拖车上(4美元ea)。-
If
f
represents the number of flip-flops and
b
represents the number of baseball hats, write a function to represent the number of flip-flops purchased as a function of unspent monies from baseball hats.
::如果 f 表示翻滚式拖车数目, b 表示棒球帽数目,请写一个函数表示以棒球帽未用钱作为功能购买的翻滚式拖车数目。
::=100-5h4美元-
Using your equation from (a), determine the number of baseball hats that can be bought if 10 flip flops were purchased.
::使用(a)的方程式,确定如果购买了10个翻滚球,可以购买的棒球帽数量。
To calculate how many hats could be bought if 10 pairs of flip flops were purchased, substitute 10 in for f , and solve for h :
::计算如果购买了10对翻转滑杆,可以购买多少帽子,f替代10顶帽子,然后解决h:
::10=100-5h4
::40=100-5小时
::5h=60
::h=12 小时=12Therefore, if 10 pairs of flip flops were purchased, there would be money left over to buy 12 baseball caps.
::因此,如果购买了10双翻滚杆,就剩下钱来购买12个棒球帽。Example 6
::例6Studies of the metabolism of alcohol consistently show that blood alcohol content (BAC) declines linearly, after rising rapidly after initial ingestion. In one study, BAC in a fasting person rose to about 0.018 % after a single drink. After an hour the level had dropped to 0.010 %.
::对酒精新陈代谢的研究始终表明,血液酒精含量(BAC)在初步摄入后迅速上升后直线下降。 在一项研究中,禁食者的酒精含量(BAC)在一次饮酒后上升至0.018 % 。 一小时后水平下降到0.010%。In order to answer the question, you must express the relationship as an equation and then use the equation.
::为了回答这个问题,你必须把关系表达为等式,然后使用等式。First, define the variables in the function and create a table.
::首先,定义函数中的变量并创建表格。The two variables are time and BAC.
::这两个变量是时间和BAC。Time BAC 0 0.018% 1 0.010% Next, calculate the rate of change.
::接下来,计算变化率。Time BAC Rate of change 0 0.018% 0 1 0.010% (0.008%) This rate of change means when the time increases by 1, the BAC decreases (since the rate of change is negative) by .008. In other words, the BAC is decreasing .008% every hour. Since we are told that BAC declines linearly, we can assume that figure stays constant.
::这一变化率意味着当时间增加1:1时,BAC就会下降(因为变化率是负的)0.008时,换句话说,BAC每小时下降0.008 % 。 由于我们被告知BAC线性下降,我们可以假设这个数字保持不变。-
Write an equation relating BAC to time in hours after drinking
t
.
::写一个方程式,将BAC与饮T后几个小时的时间联系起来。
Now we can write an equation with b representing BAC and t, the time in hours:
::现在我们可以用 b 代表 BAC 和 t 来写一个方程式, 时间在小时中 :
::b.008t+.018-
Assuming that BAC continues to decline linearly (meaning at a constant rate of change), approximately when will BAC drop to 0.002%?
::假设BAC继续线性下降(即以不变的变动率),BAC大约何时会下降到0.002%?
To learn when will the BAC reach .002%, substitute .002 in for b and solve for t .
::学习BAC何时能达到0.002%, 替换0.002%到b, 解决 t。
::002+0.008t+.018
::-016.008吨
::t=2Therefore the BAC will reach .002% after 2 hours.
::因此,BAC在2小时后将达到0.002%。Review
::回顾-
From 2002 - 2009 the number of gas stations in a certain country increased by 100 stations per year. In 2004 there were 1100 gas stations. Write a linear equation for the number of gas stations,
, as a function of time, (t,) where t = 0 represents the year 2002.
::从2002年至2009年,某些国家的加油站数量每年增加100个,2004年有1100个,为加油站数量写一个线性方程,按时间函数,(t)t=0代表2002年。
Find the vertex of the following quadratic functions and then graph them.
::查找以下二次函数的顶点,然后绘制图表。-
:xx) = 2x2 - 6x+11
-
:xx)=3(x+5)2-2
At the local downtown 4th of July fireworks celebration, the fireworks are shot by remote control into the air from a pit in the ground that is 12 feet below the earth's surface.
::在7月4日当地市区烟火节上, 烟火由遥控器射入空气中, 从地表下方12英尺的地底的坑里。-
Find an equation that models the height of an aerial bomb
t
seconds after it is shot upwards with an initial velocity of 80 ft/sec. Assume that the bomb accelerates negatively due to gravity at a rate of 32 ft/sec
2
each second.
::找到一个方程式,在空投炸弹以80英尺/秒的最初速度向上射出后几秒,以该天体炸弹的高度为模型。 假设炸弹因重力而负加速,每秒32英尺/秒。 -
Find the vertex of the quadratic function.
::查找二次函数的顶点。 -
What is the maximum height above ground level that the aerial bomb will reach?
::空中炸弹达到的地面最高高度是多少? -
How many seconds after it was launched will it take to reach that height?
::发射几秒后才能达到那个高度? -
A rock is thrown from the top of a 763ft tall building. The distance, in feet, between the rock and the ground
t
seconds after it is thrown is given by
. How long after the rock is thrown is it 430 feet from the ground?
::岩石从763英尺高的建筑顶部被抛出,在岩石抛出后几秒钟,岩石与地面之间的距离由d16t2-2-2t+763给出。岩石抛出后多久,离地面有430英尺? -
Use the vertical motion formula
to find the number of seconds it takes for a rocket launched from the ground with a starting velocity of 96 ft/s to reach an altitude of 45 ft. Round answers to the nearest tenth.
::使用垂直运动公式 h16t2+v0t+s 来寻找从地面发射火箭所需的秒数,该火箭的起始速度为96英尺/秒,以达到接近十分之一的45英尺高度。 -
The function
models the United States population in millions since 1900. Use the function P to predict the year in which the population exceeds 1 billion.
::P=0.0089t2+1.1149t+78.4491 函数模拟自1900年以来美国人口以百万计。使用P函数预测人口超过10亿的年份。 -
For which value of
x
is
if
?
::如果 f( x)\\\\\\\\\\4x2+3x, x 的值是 f( x)\\\\\\ 10 ?
Review (Answers)
::回顾(答复)Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。 -
If
f
represents the number of flip-flops and
b
represents the number of baseball hats, write a function to represent the number of flip-flops purchased as a function of unspent monies from baseball hats.