7.6 从图表中提取公式

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 从图表中提取公式

  Collapse Expand

  从图表中提取公式

  播放段落

  The graph of a cubic function starts at the point (2, 2). It passes through the point (10, -2). What is the equation of the function?
  ::立方函数的图形从点开始( 2, 2) 。 它通过点( 10, - 2) 。 该函数的方程式是什么 ?

  播放段落

  Extracting the Equation from a Graph
  ::从图表中提取公式

  播放段落

  In this concept, instead of graphing from the equation, we will now find the equation when we are given the graph.
  ::在这个概念中,我们不是用方程式绘制图表,而是用方程式绘制图表,现在,当我们得到图表时,我们就会找到方程式。

  播放段落

  Let's determine the equation of the graph below.
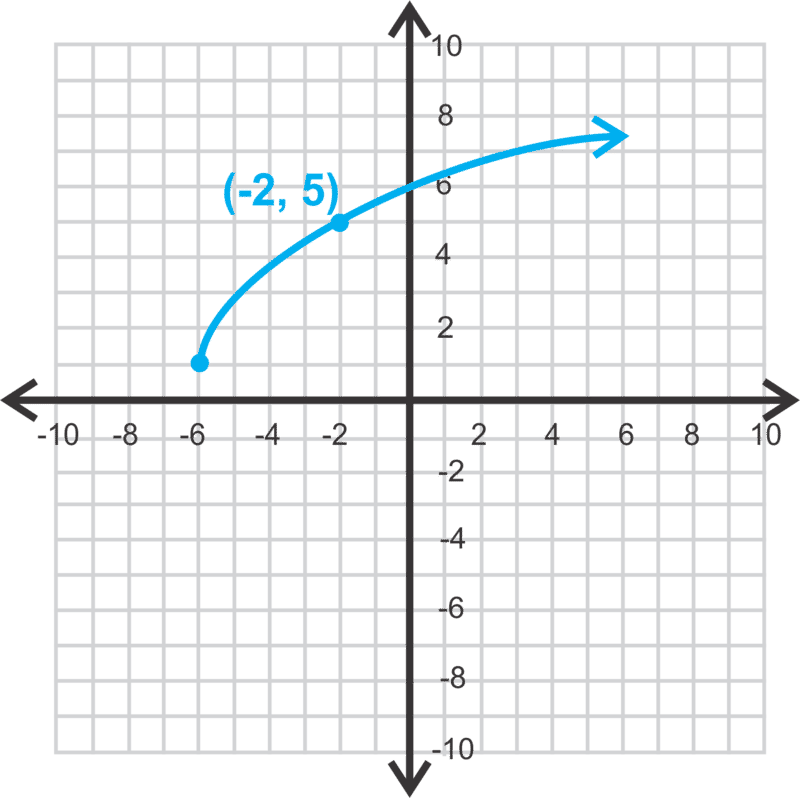
  ::我们来决定下方图的方程式

  

  播放段落

  We know this is a square root function , so the general form is $\begin{array}{r}y=a\sqrt{x-h}+k\end{array}$ . The starting point is $\begin{array}{r}(-6,1)\end{array}$ . Plugging this in for $\begin{array}{r}h\end{array}$ and $\begin{array}{r}k\end{array}$ , we have $\begin{array}{r}y=a\sqrt{x+6}+1\end{array}$ . Now, find $\begin{array}{r}a\end{array}$ , using the given point, $\begin{array}{r}(-2,5)\end{array}$ . Let’s substitute it in for $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ and solve for $\begin{array}{r}a\end{array}$ .
  ::我们知道这是一个平方根函数, 所以一般的形式是 y=ax- h+k。 起始点是 (- 6, 1) 。 开始点是 (- 6, 1) 。 将它插入 h和 k, 我们有 y=ax+6+1 。 现在, 使用给定点找到一个 (- 2, 5) 。 让我们用 x 和 y 来替换它, 然后解决一个 。

  播放段落

  $$\begin{array}{rl}5& =a\sqrt{-2+6}+1\\ 4& =a\sqrt{4}\\ 4& =2a\\ 2& =a\end{array}$$

  
  ::5=a-2+6+14=a44=2a2=a2=a

  播放段落

  The equation is $\begin{array}{r}y=2\sqrt{x+6}+1\end{array}$ .
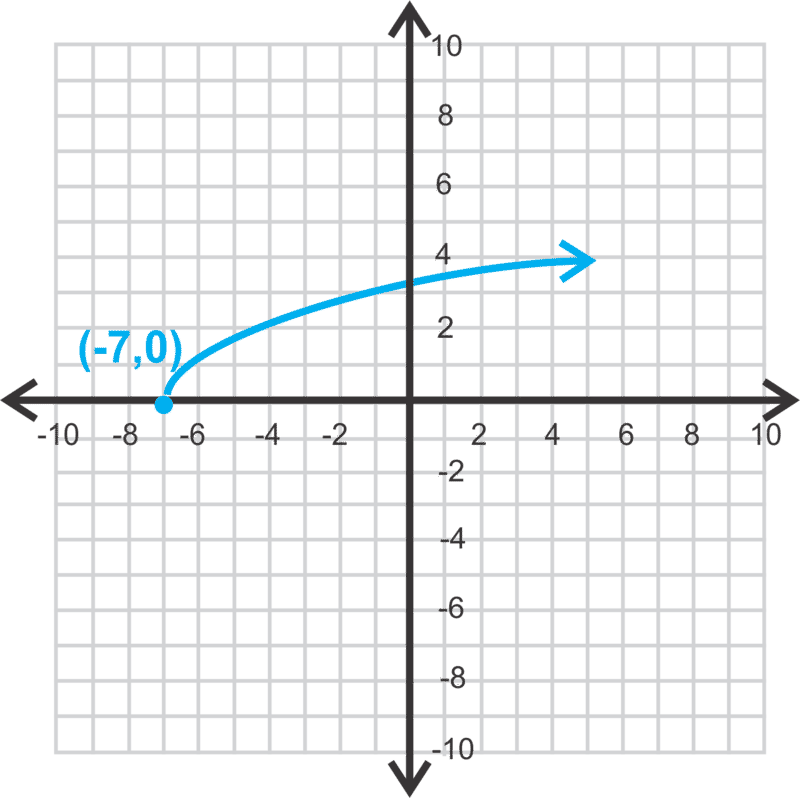
  ::方程式是 y= 2x+6+1 。

  播放段落

  Now, let's find the equation of the cubed root function where $\begin{array}{r}h=-1\end{array}$ and $\begin{array}{r}k=-4\end{array}$ and passes through $\begin{array}{r}(-28,-3)\end{array}$ .
  ::现在,让我们找到立方根函数的方程式, 位置是 h1 和 k4, 然后通过 (- 28, - 3) 。

  播放段落

  First, plug in what we know to the general equation; $\begin{array}{r}y=\sqrt[3]{x-h}+k\Rightarrow y=a\sqrt[3]{x+1}-4\end{array}$ . Now, substitute $\begin{array}{r}x=-28\end{array}$ and $\begin{array}{r}y=-3\end{array}$ and solve for $\begin{array}{r}a\end{array}$ .
  ::首先,插入我们所知道的一般方程; y=x- h3+ky=ax+13-4。 现在, 替换 x28 和 y3, 并解决 a 。

  播放段落

  $$\begin{array}{rl}-3& =a\sqrt[3]{-28+1}-4\\ 1& =-3a\\ -\frac{1}{3}& =a\end{array}$$

  
  ::- 3=a-28+13-41*3a-13=a

  播放段落

  The equation of the function is $\begin{array}{r}y=-\frac{1}{3}\sqrt[3]{x+1}-4\end{array}$ .
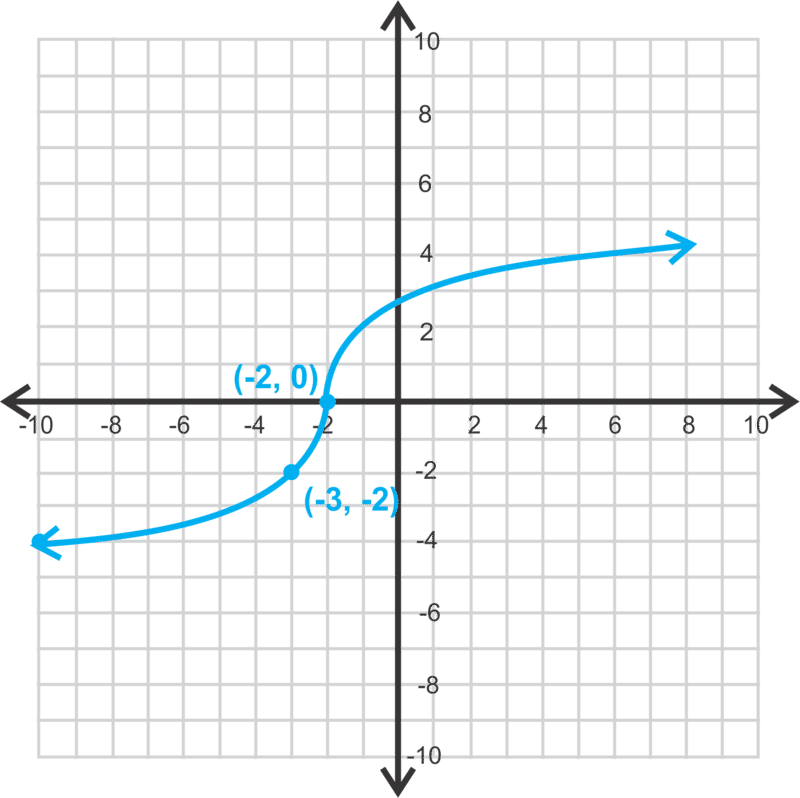
  ::函数的方程式是 y13x+13-4。

  播放段落

  Finally, let's find the equation of the function below.
  ::最后,让我们来看看以下函数的等式。

  

  播放段落

  It looks like $\begin{array}{r}(0,-4)\end{array}$ is $\begin{array}{r}(h,k)\end{array}$ . Plug this in for $\begin{array}{r}h\end{array}$ and $\begin{array}{r}k\end{array}$ and then use the second point to find $\begin{array}{r}a\end{array}$ .
  ::看起来(0, - 4) 是 (h, k.) 。 插插在 h 和 k 之间, 然后用第二点来找到一个 。

  播放段落

  $$\begin{array}{rl}-6& =a\sqrt[3]{1-0}-4\\ -2& =a\sqrt[3]{1}\\ -2& =a\end{array}$$

  
  ::- 6=a1-03-4-2=a13-2=a

  播放段落

  The equation of this function is $\begin{array}{r}y=-2\sqrt[3]{x}-4\end{array}$ .
  ::此函数的等式为 y2x3-4。

  播放段落

  When finding the equation of a cubed root function, you may assume that one of the given points is $\begin{array}{r}(h,k)\end{array}$ . Whichever point is on the “bend” is $\begin{array}{r}(h,k)\end{array}$ for the purposes of this text.
  ::当查找立方根函数的方程式时, 您可以假设给定的点之一是 (h, k) 。 无论哪个点位于“ 端点” 上, 就本文本而言, 哪一个点是 (h, k) 。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find  the equation of the function. 
  ::早些时候,有人要求你找到函数的方程式。

  播放段落

  First, plug in what we know to the general equation; $\begin{array}{r}y=\sqrt[3]{x-h}+k\Rightarrow y=a\sqrt[3]{x-2}+2\end{array}$ . Now, substitute $\begin{array}{r}x=10\end{array}$ and $\begin{array}{r}y=-2\end{array}$ and solve for $\begin{array}{r}a\end{array}$ .
  ::首先,插入我们所知道的一般方程式;y=x-h3+ky=ax-23+2。 现在, 替换 x=10 和 y2, 并解决 a 。

  播放段落

  $$\begin{array}{rl}-2& =a\sqrt[3]{10-2}+2\\ -2& =a\sqrt[3]{8}+2\\ -2& =2a+2\\ -4& =2a\\ a=-2\end{array}$$

  
  ::-2=a10-23+2-2=a83+2-2=2a+2-4=2aa=2aa=2aa2

  播放段落

  The equation of the function is $\begin{array}{r}y=-2\sqrt[3]{x-2}+2\end{array}$ .
  ::函数的方程式是 y2x-23+2。

  播放段落

  Example 2
  ::例2

  播放段落

  Find the equation of the following function.
  ::查找以下函数的方程式。

  

  播放段落

  Substitute what you know into the general equation to solve for $\begin{array}{r}a\end{array}$ . From the final practice problem above, you may assume that $\begin{array}{r}(5,8)\end{array}$ is $\begin{array}{r}(h,k)\end{array}$ and $\begin{array}{r}(-3,7)\end{array}$ is $\begin{array}{r}(x,y)\end{array}$ .
  ::以您所知道的 代替一般方程 。 从以上最后练习问题, 您可以假设 (5, 8) (h, k) 和 (- 3, 7) (x,y) (x,y) 。

  播放段落

  $$\begin{array}{rl}y& =a\sqrt[3]{x-5}+8\\ 7& =a\sqrt[3]{-3-5}+8\\ -1& =-2a\\ \frac{1}{2}& =a\end{array}$$

  
  ::y=x-53+87=a-3-53+8-1=2a12=a

  播放段落

  The equation of this function is $\begin{array}{r}y=\frac{1}{2}\sqrt[3]{x-5}+8\end{array}$ .
  ::此函数的方程式是 Y=12x-53+8。

  播放段落

  Example 3
  ::例3

  播放段落

  Find the equation of the following function.
  ::查找以下函数的方程式。

  

  播放段落

   Substitute what you know into the general equation to solve for $\begin{array}{r}a\end{array}$ . From the graph, the starting point, or $\begin{array}{r}(h,k)\end{array}$ is $\begin{array}{r}(4,-11)\end{array}$ and $\begin{array}{r}(13,1)\end{array}$ are a point on the graph.
  ::将您所知道的替换为要解答的普通方程式。 从图形中, 起始点或( h, k) 是 (4, - 11) 和 (13, 1) 是图上的一个点 。

  播放段落

  $$\begin{array}{rl}y& =a\sqrt{x-4}-11\\ 1& =a\sqrt{13-4}-11\\ 12& =3a\\ 4& =a\end{array}$$

  
  ::y=ax - 4 - 111=a13 - 4 - 1112=3a4=a

  播放段落

  The equation of this function is $\begin{array}{r}y=4\sqrt{x-4}-11\end{array}$ .
  ::此函数的等式为y=4x-4-11。

  播放段落

  Example 4
  ::例4

  播放段落

  Find the equation of a square root equation with a starting point of $\begin{array}{r}(-5,-3)\end{array}$ and passes through $\begin{array}{r}(4,-6)\end{array}$ .
  ::查找平方根方程式的方程式,起点为(-5、-3)和通过(4、-6)。

  播放段落

  Substitute what you know into the general equation to solve for $\begin{array}{r}a\end{array}$ . From the graph, the starting point, or $\begin{array}{r}(h,k)\end{array}$ is $\begin{array}{r}(-5,-3)\end{array}$ and $\begin{array}{r}(4,-6)\end{array}$ are a point on the graph.
  ::将您所知道的替换为要解答的普通方程。 从图形中,起点或(h,k)是(-5,-3)和(4,-6)是图形上的点。

  播放段落

  $$\begin{array}{rl}y& =a\sqrt{x+5}-3\\ -6& =a\sqrt{4+5}-3\\ -3& =3a\\ -1& =a\end{array}$$

  
  ::y= 轴+5 - 3 - 6= a4+5 - 3 - 3= 3a - 1=a

  播放段落

  The equation of this function is $\begin{array}{r}y=-\sqrt{x+5}-3\end{array}$ .
  ::此函数的方程式是 yx+5-3。

  播放段落

  Review
  ::回顾

  播放段落

  Write the equation for each function graphed below.
  ::写下以下图表的每个函数的方程式 。

  1. 
  2. 
  3. 
  4. 
  5. 
  6. 
  7. 
  8. 
  9. 
  播放段落
  10. Write the equation of a square root function with starting point $\begin{array}{r}(-6,-3)\end{array}$ passing through $\begin{array}{r}(10,-15)\end{array}$ .
      ::写入平方根函数的方程式,起点(-6-3)通过(10,-15)。
  播放段落
  11. Write the equation of a cube root function with $\begin{array}{r}(h,k)=(2,7)\end{array}$ passing through $\begin{array}{r}(10,11)\end{array}$ .
      ::写入立方根函数的方程式(h,k)=(2,7)通过(10,11)的方程式。
  播放段落
  12. Write the equation of a square root function with starting point $\begin{array}{r}(-1,6)\end{array}$ passing through $\begin{array}{r}(3,16)\end{array}$ .
      ::写入平方根函数的方程式,其起点(-1,6)通过(3,16)。
  播放段落
  13. Write the equation of a cubed root function with $\begin{array}{r}(h,k)=(-1,6)\end{array}$ passing through $\begin{array}{r}(7,16)\end{array}$ .
      ::以 (h,k) =(-1,6) 通过 (7,16) 写入立方根函数的方程式。
  播放段落
  14. Write the equation of a cubed root function with $\begin{array}{r}(h,k)=(7,16)\end{array}$ passing through $\begin{array}{r}(-1,6)\end{array}$ .
      ::以 (h,k) =(7,16) 通过 (-1,6) 写入立方根函数的方程式。
  播放段落
  15. How do the two equations above differ? How are they the same?
      ::上述两个方程式有何不同?它们如何相同?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。