Course: 7..11 反函数 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 反函数

Collapse Expand
反函数
A planet's maximum distance from the sun (in astronomical units) is given by the formula $\begin{aligned} d = p^{\frac{2}{3}} \end{aligned}$ , were p is the period (in years) of the planet's orbit around the sun. What is the inverse of this function?
::公式 d=p23 给出的行星与太阳的最大距离( 天文单位) 。公式 d=p23 给出的行星与太阳的最大距离是行星围绕太阳轨道的周期( 年)。这个函数的反面是什么?

Inverse Functions
::反函数

By now, you are probably familiar with the term “inverse”. Multiplication and division are inverses of each other. More examples are addition and subtraction and the square and square root. We are going to extend this idea to functions. An inverse relation maps the output values to the input values to create another relation. In other words, we switch the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ values. The domain of the original relation becomes the range of the inverse relation and the range of the original relation becomes the domain of the inverse relation.
::现在,您可能已经熟悉“反向”一词。乘法和除法是相互反向的。更多的例子是添加和减法, 平方根和正方根。我们将把这个概念扩展为函数。反向映射输出值到输入值, 以创建另一个关系。换句话说, 我们交换 x 和 y 值。原始关系的域成为反向关系的范围, 而原始关系的范围则成为反向关系的范围。

Let's find the inverse mapping of $\begin{aligned} S = {(6, - 1), (- 2, - 5), (- 3, 4), (0, 3), (2, 2)} \end{aligned}$ .
::让我们找到S(6)-1(-2)-5(-3,4),(0),(3),(2,2)}的反向映射图。

Here, we will find the inverse of this relation by mapping it over the line $\begin{aligned} y = x \end{aligned}$ . As was stated above in the definition, the inverse relation switched the domain and range of the original function. So, the inverse of this relation, $\begin{aligned} S \end{aligned}$ , is $\begin{aligned} S^{- 1} \end{aligned}$ (said “ $\begin{aligned} s \end{aligned}$ inverse”) and will flip all the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ values.
::在这里,我们将通过在 y=x 线上绘制此关系图来发现反向关系。正如上文定义中所说,反向关系改变了原始函数的域和范围。因此,这一关系的反向关系S,是S-1(表示“反向”),并将翻转所有 x 和 y 值。

$\begin{aligned} S^{- 1} = {(- 1, 6), (- 5, - 2), (4, - 3), (3, 0), (2, 2)} \end{aligned}$
::S-1(-1,6),(-5,-2),(4)-3,(3,0),(2,2)}

If we plot the two relations on the $\begin{aligned} x - y \end{aligned}$ plane, we have:
::如果我们在X-y平面上勾画这两个关系,我们有:

The blue points are all the points in $\begin{aligned} S \end{aligned}$ and the red points are all the points in $\begin{aligned} S^{- 1} \end{aligned}$ . Notice that the points in $\begin{aligned} S^{- 1} \end{aligned}$ are a reflection of the points in $\begin{aligned} S \end{aligned}$ over the line, $\begin{aligned} y = x \end{aligned}$ . All inverses have this property.
::蓝色点是S中的所有点,红色点是S-1中的所有点。请注意,S-1中的点反映了y=x线上S的点。所有反面都有这一属性。

If we were to fold the graph on $\begin{aligned} y = x \end{aligned}$ , each inverse point $\begin{aligned} S^{- 1} \end{aligned}$ should lie on the original point from $\begin{aligned} S \end{aligned}$ . The point $\begin{aligned} (2, 2) \end{aligned}$ lies on this line, so it has no reflection. Any value on this line will remain the same.
::如果我们在 y=x 上折叠图表, 则每个反方向的 S-1 点应该位于 S 的原点上。点 2, 2 位于此线上, 所以它没有反射。此线上的任何值都会保持不变。

Domain of $\begin{aligned} S \end{aligned}$ : $\begin{aligned} x \in {6, - 2, - 3, 0, 2} \end{aligned}$
::S域域: x6,-2,-3,3,0,2}

Range of $\begin{aligned} S \end{aligned}$ : $\begin{aligned} y \in {- 1, - 5, 4, 3, 2} \end{aligned}$
::S范围:y1,-5,4,3,2}

Domain of $\begin{aligned} S^{'} \end{aligned}$ : $\begin{aligned} x \in {- 1, - 5, 4, 3, 2} \end{aligned}$
::S 域域: x1, - 5, 4, 3, 2}

Range of $\begin{aligned} S^{'} \end{aligned}$ : $\begin{aligned} y \in {6, - 2, - 3, 0, 2} \end{aligned}$
::S`范围:y6,-2,-3,3,0,2}

By looking at the domains and ranges of $\begin{aligned} S \end{aligned}$ and $\begin{aligned} S^{- 1} \end{aligned}$ , we see that they are both functions (no $\begin{aligned} x \end{aligned}$ -values repeat). When the inverse of a function is also a function, we say that the original function is a one-to-one function . Each value maps one unique value onto another unique value.
::通过查看 S 和 S-1 的域和范围,我们看到它们都是函数( 没有 x 值重复 ) 。当函数的反向也是一个函数时, 我们说原始函数是一个一对一的函数。每个值将一个独特的值映射为另一个独特的值。

Now, let's find the inverse of $\begin{aligned} f (x) = \frac{2}{3} x - 1 \end{aligned}$ .
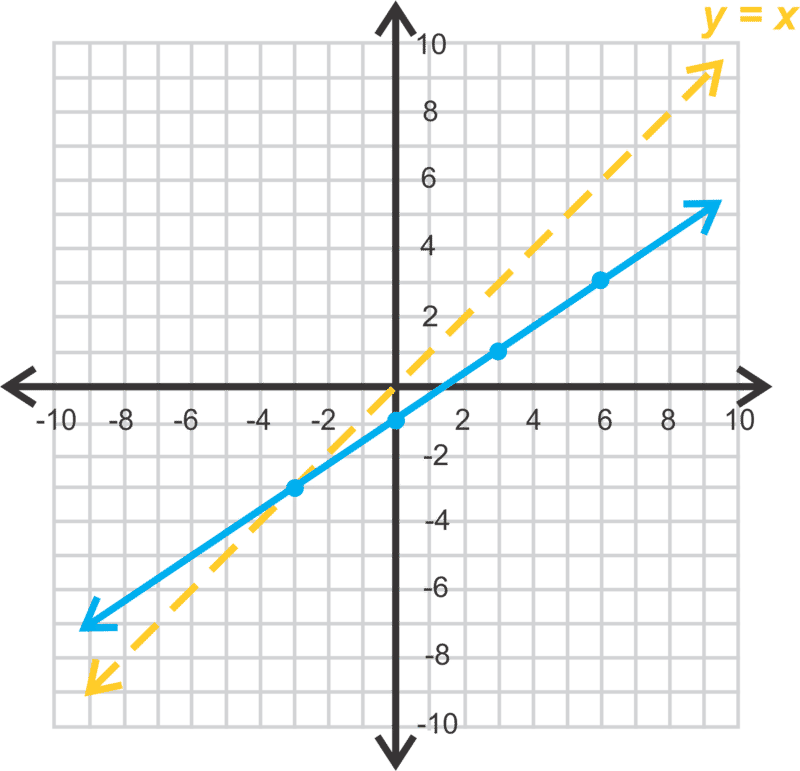
::现在,让我们找到f(x)=23x-1的逆数。

This is a linear function. Let’s solve by doing a little investigation. First, draw the line along with $\begin{aligned} y = x \end{aligned}$ on the same set of axes.
::这是一个线性函数。让我们通过小小调查来解决。首先, 在同一组轴上与 y=x 一起绘制线条。

Notice the points on the function (blue line). Map these points over $\begin{aligned} y = x \end{aligned}$ by switching their $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ values. You could also fold the graph along $\begin{aligned} y = x \end{aligned}$ and trace the reflection.
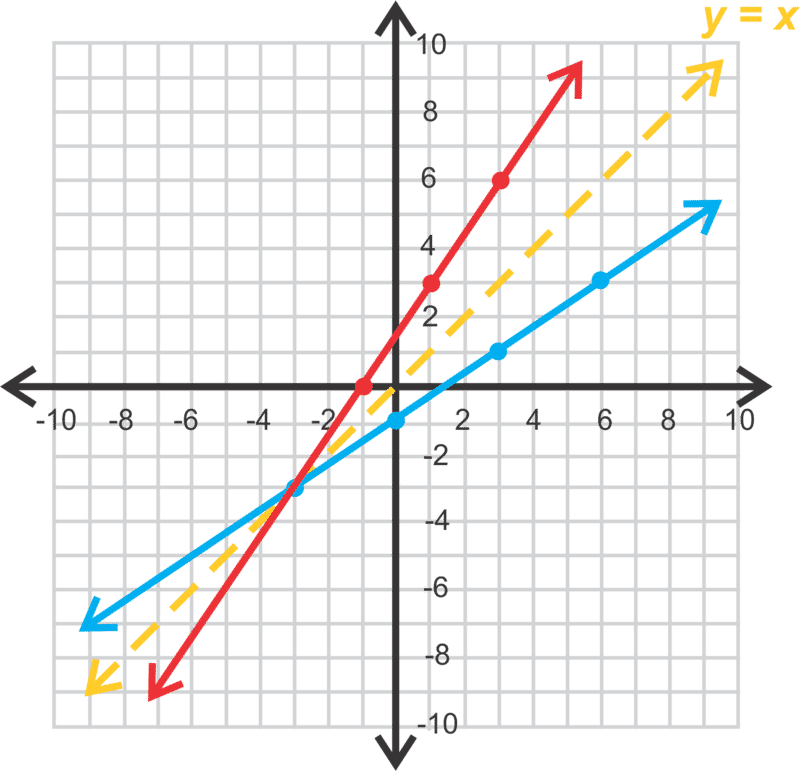
::注意函数( 蓝色线条) 上的点。通过切换它们的 x 和 y 值, 在 y =x 上绘制这些点。您也可以沿着 y =x 折叠图形, 并跟踪反射。

The red line in the graph to the right is the inverse of $\begin{aligned} f (x) = \frac{2}{3} x - 1 \end{aligned}$ . Using slope triangles between (-1, 0) and (1, 3), we see that the slope is $\begin{aligned} \frac{3}{2} \end{aligned}$ . Use (-1, 0) to find the $\begin{aligned} y \end{aligned}$ -intercept.
::图向右的红线是 f(x)=23x-1. 使用(-1,0)和(1,3)之间的斜度三角形,我们看到斜度是32,使用(-1,0)来查找 Y 接口。

$\begin{aligned} f^{- 1} (x) & = \frac{3}{2} x + b \\ 0 & = \frac{3}{2} (- 1) + b \\ \frac{3}{2} & = b \end{aligned}$

::f- 1 (x) = 32x+b0= 32(- 1)+b32=b

The equation of the inverse, read “ $\begin{aligned} f \end{aligned}$ inverse”, is $\begin{aligned} f^{- 1} (x) = \frac{3}{2} x + \frac{3}{2} \end{aligned}$ .
::倒数方程式为F-1(x)=32x+32。

You may have noticed that the slopes of $\begin{aligned} f \end{aligned}$ and $\begin{aligned} f^{- 1} \end{aligned}$ are reciprocals of each other. This will always be the case for linear functions. Also, the $\begin{aligned} x \end{aligned}$ -intercept of $\begin{aligned} f \end{aligned}$ becomes the $\begin{aligned} y \end{aligned}$ -intercept of $\begin{aligned} f^{- 1} \end{aligned}$ and vice versa.
::您可能注意到 f 和 f - 1 的斜坡是相互对等的。线性函数总是这样。此外, f 的 x intermission 成为 f - 1 的 y intermission, 反之亦然。

Alternate Method: There is also an algebraic approach to finding the inverse of any function. Let’s repeat this example using algebra.
::替代方法: 也有一种代数法来查找任何函数的反向。让我们用代数重复这个例子。

Step 1: Change $\begin{aligned} f (x) \end{aligned}$ to $\begin{aligned} y \end{aligned}$ .
::第1步:将f(x)改为y。

$\begin{aligned} y = \frac{2}{3} x - 1 \end{aligned}$
::y=23x-1

Step 2: Switch the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . Change $\begin{aligned} y \end{aligned}$ to $\begin{aligned} y^{- 1} \end{aligned}$ for the inverse.
::第2步:将 x 和 y 切换为 y - 1 。

$\begin{aligned} x = \frac{2}{3} y^{- 1} - 1 \end{aligned}$
::x=23y-1-1-1

Step 3: Solve for $\begin{aligned} y^{'} \end{aligned}$ .
::步骤3:解决你。

$\begin{aligned} x & = \frac{2}{3} y^{- 1} - 1 \\ \frac{3}{2} (x + 1) & = \frac{3}{2} \cdot (\frac{2}{3} y^{- 1}) \\ \frac{3}{2} x + \frac{3}{2} & = y^{- 1} \end{aligned}$

::x=23y- 1- 132( x+1) = 32( 23y- 1) 32x+32=y-1

The algebraic method will work for any type of function.
::代数法适用于任何类型的函数。

Finally, let's determine if $\begin{aligned} g (x) = \sqrt{x - 2} \end{aligned}$ and $\begin{aligned} f (x) = x^{2} + 2 \end{aligned}$ are inverses of each other.
::最后,让我们确定 g( x) =x- 2 和 f( x) =x2+2 是否彼此反相。

There are two different ways to determine if two functions are inverses of each other. The first, is to find $\begin{aligned} f^{- 1} \end{aligned}$ and $\begin{aligned} g^{- 1} \end{aligned}$ and see if $\begin{aligned} f^{- 1} = g \end{aligned}$ and $\begin{aligned} g^{- 1} = f \end{aligned}$ .
::确定两个函数是否相互反差有两种不同的方法。第一个是查找 f-1 和 g-1 , 并查看 f-1= g 和 g-1= f 。

$\begin{aligned} x & = \sqrt{y^{- 1} - 2} & x = (y^{- 1})^{2} + 2 \\ x^{2} & = y^{- 1} - 2 & a n d & x - 2 = (y^{- 1})^{2} \\ x^{2} + 2 & = y^{- 1} = g^{- 1} (x) & \pm \sqrt{x - 2} = y^{- 1} = f^{- 1} (x) \end{aligned}$

::xy - 1 - 2 x= (y - 1) 2+2x2=y - 1 - 2 和x-2= (y - 1) 2x2+2=y - 1=g - 1 (x) =x-2=y-1=y-1=f - 1(x)

Notice the $\begin{aligned} \pm \end{aligned}$ sign in front of the square root for $\begin{aligned} f^{- 1} \end{aligned}$ . That means that $\begin{aligned} g^{- 1} \end{aligned}$ is $\begin{aligned} \sqrt{x - 2} \end{aligned}$ and $\begin{aligned} - \sqrt{x - 2} \end{aligned}$ .
::注意 f - 1 在正方根前面的 + 符号。这意味着 g - 1 是 x-2 和 - x-2 。

Therefore, $\begin{aligned} f^{- 1} \end{aligned}$ is not really a function because it fails the vertical line test. However, if you were to take each part separately, individually, they are functions. You can also think about reflecting $\begin{aligned} f (x) \end{aligned}$ over $\begin{aligned} y = x \end{aligned}$ . It would be a parabola on its side, which is not a function.
::因此, f- 1 不是一个函数, 因为它失败了垂直线测试。但是, 如果您单独选择每个部分, 它们就是函数。您也可以考虑在 y=x 上反射 f( x) 。它的侧面将是一个抛物线, 它不是一个函数。

The inverse of $\begin{aligned} g \end{aligned}$ would then be only half of the parabola, see below. Despite the restrictions on the domains, $\begin{aligned} f \end{aligned}$ and $\begin{aligned} g \end{aligned}$ are inverses of each other.
::g的反比只有抛物线的一半,见下文,尽管对域有限制,f和g是相反的。

Alternate Method: The second, and easier, way to determine if two functions are inverses of each other is to use composition. If $\begin{aligned} f \circ g = g \circ f = x \end{aligned}$ , then $\begin{aligned} f \end{aligned}$ and $\begin{aligned} g \end{aligned}$ are inverses of each other. Think about it; if everything cancels out and all that remains is $\begin{aligned} x \end{aligned}$ , each operation within the functions are opposites, making the functions “opposites” or inverses of each other.
::替代方法: 确定两个函数是否相互反比的第二个和比较容易的方法是使用组成。如果 fg=gff=x, 那么f和g是相互反比的。仔细想想; 如果一切取消, 剩下的全部为 x, 函数内的每个操作都是相反的, 使函数“ 反对者” 或反比。

$\begin{aligned} f \circ g & = \sqrt{(x^{2} + 2) - 2} & g \circ f = {\sqrt{x - 2}}^{2} + 2 \\ = \sqrt{x^{2}} & a n d & = x - 2 + 2 \\ = x & = x \end{aligned}$

::f=x-22+2=x2=x2=x2=x2=xx=xxx=x2+2=xx

Because $\begin{aligned} f \circ g = g \circ f = x \end{aligned}$ , $\begin{aligned} f \end{aligned}$ and $\begin{aligned} g \end{aligned}$ are inverses of each other. Both $\begin{aligned} f \circ g = x \end{aligned}$ and $\begin{aligned} g \circ f = x \end{aligned}$ in order for $\begin{aligned} f \end{aligned}$ and $\begin{aligned} g \end{aligned}$ to be inverses of each other.
::因为 fg=gf=x, f 和 g是彼此的反义。 fg=x 和 gf=x 都是为了让 f 和 g 成为彼此的反义。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the inverse of the function $\begin{aligned} d = p^{\frac{2}{3}} \end{aligned}$ .
::早些时候,您被要求找到函数 d=p23 的反方向。

In the function $\begin{aligned} d = p^{\frac{2}{3}} \end{aligned}$ , d is the equivalent of y and p is the equivalent of x . So rewrite the equation and follow the step-by-step process illustrated above.
::在函数 d=p23, d 等于y, p 等于 x。所以重写方程, 并遵循上述逐步过程。

$\begin{aligned} y = x^{\frac{2}{3}} \end{aligned}$ ,
::y=x23, y=23;

Switch the $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$ . Change $\begin{aligned} y \end{aligned}$ to $\begin{aligned} y^{- 1} \end{aligned}$ for the inverse.
::切换 x 和 y 。更改 y 到 y - 1 以换反。

$\begin{aligned} x = (y^{- 1})^{\frac{2}{3}} \end{aligned}$
::x=(y- 1) 23

Solve for $\begin{aligned} y^{'} \end{aligned}$ .
::解决你。

$\begin{aligned} x = (y^{- 1})^{\frac{2}{3}} \\ x^{\frac{3}{2}} = (y^{- 1})^{\frac{2}{3} \cdot \frac{3}{2}} \\ x^{\frac{3}{2}} = y^{- 1} \end{aligned}$

::x= (y- 1) 23x32= (y- 1) 23- 32x32=y-1

Now replace y and x with d and p . The inverse d is $\begin{aligned} p^{\frac{3}{2}} \end{aligned}$ .
::将 y 和 x 替换为 d 和 p。逆差是 p32 。

Example 2
::例2

Find the inverse of $\begin{aligned} g (x) = - \frac{3}{4} x + 12 \end{aligned}$ algebraically.
::查找 g( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ x+12 代数的反义。

$\begin{aligned} y & = - \frac{3}{4} x + 12 \\ x & = - \frac{3}{4} y^{- 1} + 12 \\ x - 12 & = - \frac{3}{4} y^{- 1} \\ - \frac{4}{3} (x - 12) & = y^{- 1} \\ g^{- 1} (x) & = - \frac{4}{3} x + 16 \end{aligned}$

::y34x+12x34y- 1+12x-1234y- 1 - 43(x- 12)=y- 1g- 1(x)43x+16

Example 3
::例3

Find the inverse of $\begin{aligned} f (x) = 2 x^{3} + 5 \end{aligned}$ algebraically. Is the inverse a function?
::查找 f(x) = 2x3+5 的反数值。反数值是一个函数吗?

$\begin{aligned} y & = 2 x^{3} + 5 \\ x & = 2 (y^{- 1})^{3} + 5 \\ x - 5 & = 2 (y^{- 1})^{3} \\ \frac{x - 5}{2} & = (y^{- 1})^{3} \\ f^{- 1} (x) & = \sqrt[3]{\frac{x - 5}{2}} \end{aligned}$

::y=2x3+5x=2(y-1)3+5x-5=2(y-1)3x-52=(y-1)3f-1(x)=x-523

Yes, $\begin{aligned} f^{- 1} \end{aligned}$ is a function. Plot in your graphing calculator if you are unsure and see if it passes the vertical line test.
::是的, f- 1 是一个函数。如果您不确定, 请在图形计算器中绘制, 看看它是否通过垂直线测试。

Example 4
::例4

Determine if $\begin{aligned} h (x) = 4 x^{4} - 7 \end{aligned}$ and $\begin{aligned} j (x) = \frac{1}{4} \sqrt[4]{x - 7} \end{aligned}$ are inverses of each other using compositions.
::确定 h( x) = 4x4-7 和 j( x) = 14x- 74 是否使用组成为对方的反义。

First, find $\begin{aligned} h (j (x)) \end{aligned}$ .
::首先,找到h(j(x)).

$\begin{aligned} h (j (x)) & = 4 {(\frac{1}{4} \sqrt[4]{x + 7})}^{4} - 7 \\ = 4 \cdot {(\frac{1}{4})}^{4} x + 7 - 7 \\ = \frac{1}{64} x \end{aligned}$

::h(j(xx)) = 4(14x+744) - 7= 4(144x) - 7= 4(144x) - 7+7= 164x

Because $\begin{aligned} h (j (x)) \neq x \end{aligned}$ , we know that $\begin{aligned} h \end{aligned}$ and $\begin{aligned} j \end{aligned}$ are not inverses of each other. Therefore, there is no point to find $\begin{aligned} j (h (x)) \end{aligned}$ .
::因为h(j(x))x,我们知道h和j并非彼此的反义。因此,没有必要找到j(h(x))。

Review
::回顾

Write the inverses of the following functions. State whether or not the inverse is a function.
::写入下列函数的反白。请说明反白是否函数。

$\begin{aligned} (2, 3), (- 4, 8), (- 5, 9), (1, 1) \end{aligned}$

$\begin{aligned} (9, - 6), (8, - 5), (7, 3), (4, 3) \end{aligned}$

Find the inverses of the following functions algebraically. Note any restrictions to the domain of the inverse functions.
::查找以下函数的反函数代数。请注意对反函数域的任何限制。

$\begin{aligned} f (x) = 6 x - 9 \end{aligned}$
:xx)=6x-9)

$\begin{aligned} f (x) = \frac{1}{4 x + 3} \end{aligned}$
:xx)=14x+3

$\begin{aligned} f (x) = \sqrt{x + 7} \end{aligned}$
:xx)=x+7)

$\begin{aligned} f (x) = x^{2} + 5 \end{aligned}$
:xx)=x2+5

$\begin{aligned} f (x) = x^{3} - 11 \end{aligned}$
:xx)=x3-11)

$\begin{aligned} f (x) = \sqrt[5]{x + 16} \end{aligned}$
:xx)=x+165

Determine whether $\begin{aligned} f \end{aligned}$ and $\begin{aligned} g \end{aligned}$ are inverses of each other by checking to see whether finding $\begin{aligned} f \circ g = x \end{aligned}$ or $\begin{aligned} g \circ f = x \end{aligned}$ . You do not need to show both.
::确定 f 和 g 是对方的反义值, 检查是否找到 fg=x 或 gf=x 。您不需要同时显示。

$\begin{aligned} f (x) = \frac{2}{3} x - 14 \end{aligned}$ and $\begin{aligned} g (x) = \frac{3}{2} x + 21 \end{aligned}$
:x) = 23x- 14 和 g(x) = 32x+21

$\begin{aligned} f (x) = \frac{x + 5}{8} \end{aligned}$ and $\begin{aligned} g (x) = 8 x + 5 \end{aligned}$
:xx)=x+58和g(x)=8x+5

$\begin{aligned} f (x) = \sqrt[3]{3 x - 7} \end{aligned}$ and $\begin{aligned} g (x) = \frac{x^{3}}{3} - 7 \end{aligned}$
:xx)=3x-73和g(x)=x33-7)

$\begin{aligned} f (x) = \frac{x}{x - 9}, x \neq 9 \end{aligned}$ and $\begin{aligned} g (x) = \frac{9 x}{x - 1} \end{aligned}$
:xx) =xx-9,x9 和 g(x) = 9xx-1

Find the inverses of the following functions algebraically. Note any restrictions to the domain of the inverse functions. These problems are a little trickier as you will need to factor out the $\begin{aligned} y \end{aligned}$ variable to solve. Use the example below as a guide.
::查找以下函数的反函数代数。请注意对反函数域的任何限制。这些问题比较棘手,因为您需要将 y 变量考虑在内才能解决。请使用下面的示例作为指南。

$\begin{aligned} f (x) = \frac{3 x + 13}{2 x - 11} \end{aligned}$
:xx)=3x+132x-11)

Example:
::示例:

$\begin{aligned} x = \frac{3 y + 13}{2 y - 11} \end{aligned}$ First, switch $\begin{aligned} x \end{aligned}$ and $\begin{aligned} y \end{aligned}$
::x=3y+132y- 11 首先, 开关 x 和 y

$\begin{aligned} 2 x y - 11 x = 3 y + 13 \end{aligned}$ Multiply both sides by $\begin{aligned} 2 y - 11 \end{aligned}$ to eliminate the fraction
::2xy- 11x=3y+13 将两边乘以 2y- 11 以除去分数

$\begin{aligned} 2 x y - 3 y = 11 x + 13 \end{aligned}$ Now rearrange the terms to get both terms with $\begin{aligned} y \end{aligned}$ in them on one side and everything else on the other side
::2xy- 3y= 11x+13 立即重新排列条件, 以在单面和另一面获得条件。

$\begin{aligned} y (2 x - 3) = 11 x + 13 \end{aligned}$ Factor out the $\begin{aligned} y \end{aligned}$
::y( 2x- 3) = 11x+13 乘以 Y

$\begin{aligned} y = \frac{11 x + 13}{2 x - 3} \end{aligned}$ Finally, Divide both sides by $\begin{aligned} 2 x - 3 \end{aligned}$ to isolate $\begin{aligned} y \end{aligned}$ .
::y=11x+132x-3 最后, 将两边除以 2x-3 来分隔 y 。

So, the inverse of $\begin{aligned} f (x) = \frac{3 x + 13}{2 x - 11}, x \neq \frac{11}{2} \end{aligned}$ is $\begin{aligned} f^{- 1} (x) = \frac{11 x + 13}{2 x - 3}, x \neq \frac{3}{2} \end{aligned}$ .
::因此, f( x) =3x+132x- 11,x* 112 的反义为 f-1( x) = 11x+132x-3,x* 32。

$\begin{aligned} f (x) = \frac{x + 7}{x}, x \neq 0 \end{aligned}$
:xx) =x+7x,x=0

$\begin{aligned} f (x) = \frac{x}{x - 8}, x \neq 8 \end{aligned}$
:xx) =xxx-8,x8

Multi-step problem
::多步骤问题

In many countries, the temperature is measured in degrees Celsius. In the US we typically use degrees Fahrenheit. For travelers, it is helpful to be able to convert from one unit of measure to another. The following problem will help you learn to do this using an inverse function.

The temperature at which water freezes will give us one point on a line in which $\begin{aligned} x \end{aligned}$ represents the degrees in Celsius and $\begin{aligned} y \end{aligned}$ represents the degrees in Fahrenheit. Water freezes at 0 degrees Celsius and 32 degrees Fahrenheit so the first point is (0, 32). The temperature at which water boils gives us the second point (100, 212), because water boils at 100 degrees Celsius or 212 degrees Fahrenheit. Use this information to show that the equation to convert from Celsius to Fahrenheit is $\begin{aligned} y = \frac{9}{5} x + 32 \end{aligned}$ or $\begin{aligned} F = \frac{9}{5} C + 32 \end{aligned}$ .
::水冻结的温度将让我们在一条线上有一个点,其中x代表摄氏度,y代表华氏度。水冻结在0摄氏度和32摄氏度,因此第一个点是(0,32)。水沸腾的温度给我们第二个点(100,212),因为水沸腾在100摄氏度或212华氏度。利用这一信息显示,从摄氏度转换为法氏度的方程是y=95x+32或F=95C+32。

Find the inverse of the equation above by solving for $\begin{aligned} C \end{aligned}$ to derive a formula that will allow us to convert from Fahrenheit to Celsius.
::找到上面方程式的反面, 解决 C 得出一个公式, 使我们能够从法赫里内海特转换成摄氏。

Show that your inverse is correct by showing that the composition of the two functions simplifies to either $\begin{aligned} F \end{aligned}$ or $\begin{aligned} C \end{aligned}$ (depending on which one you put into the other.)
::显示两个函数的构成简化为 F 或 C (取决于您将哪个函数简化为另一个函数), 以此显示您的反向是正确的。

::在许多国家, 温度以摄氏度测量。在美国, 我们通常使用华氏度。对于旅行者来说, 能够将水温从一个单位转换为另一个单位是有用的。下述问题有助于您学习使用反函数来进行这一转换。水冻结的温度将给我们带来一个点, 在一条线上, x 代表摄氏度, y 代表华氏度。水冻结在 0 摄氏度和 32 华氏 32 度, 因此第一个点是 0, 32 。水沸腾的温度给了我们第二点( 100, 212 ) , 因为水沸腾在100 摄氏度或 212 华氏度 Fahrenheit 。使用此信息显示, 从摄氏度转换为法赫伦海特的方程式是 y= 95x+ 32 或 F= 95C+32 。找到以上方程的反向点, 解决 C 以得出一个公式, 使我们能够从法赫伦海特转换为摄氏度。。显示两个函数的构成为 F或 C 。。正确。

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

反函数

Inverse Functions ::反函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Inverse Functions
::反函数

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)