8.2 指数衰落功能

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 指数衰落函数

  Collapse Expand

  指数衰落函数

  播放段落

  The population of a city was 10,000 in 2012 and is declining at a rate of 5% each year. If this decay rate continues, what will the city's population be in 2017?
  ::2012年,城市人口为10,000人,每年以5%的速度下降。 如果这一衰落率继续下去,2017年城市人口会是多少?

  播放段落

  Exponential Decay Function
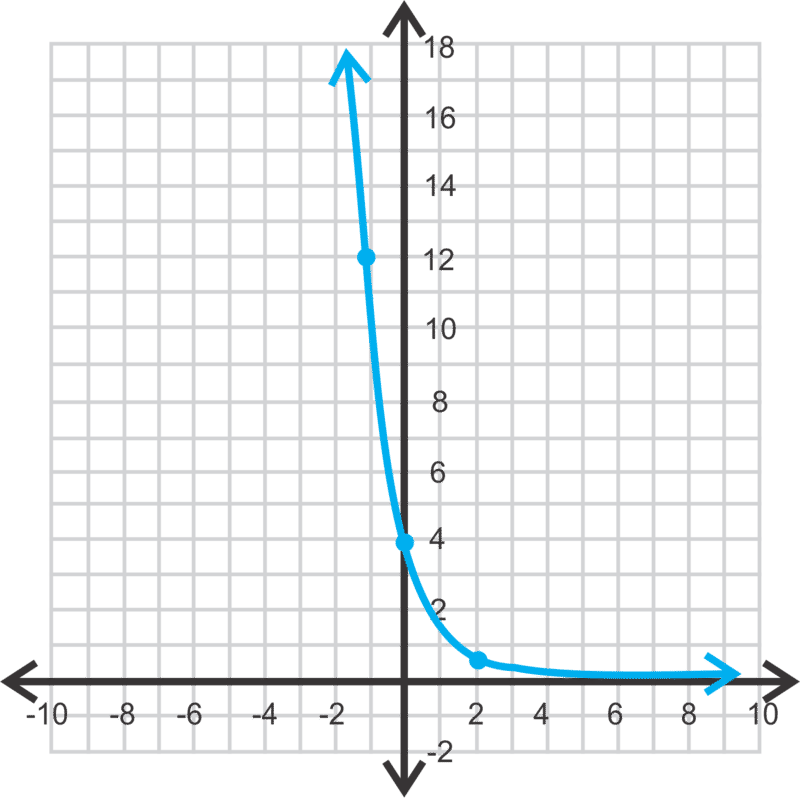
  ::指数衰落函数

  播放段落

  Previously, we have only addressed functions where $\begin{align*}|b|>1\end{align*}$ . So, what happens when $\begin{align*}b\end{align*}$ is less than 1? Let’s analyze $\begin{align*}y=\left(\frac{1}{2}\right)^x\end{align*}$ .
  ::之前,我们只处理“b”1的功能。那么,当b小于1时会怎样?让我们分析y=(12)x。

  播放段落

  Graph $\begin{align*}y=\left(\frac{1}{2}\right)^x\end{align*}$ and compare it to $\begin{align*}y=2^x\end{align*}$ .
  ::图y=( 12) x 并将其与 y= 2x 比较。

  播放段落

  Let’s make a table of both functions and then graph.
  ::让我们绘制一个两个函数的表格,然后绘制图表。

  

  $\begin{align*}x\end{align*}$	$\begin{align*}\left(\frac{1}{2}\right)^x\end{align*}$	$\begin{align*}2^x\end{align*}$
  3	$\begin{align*}\left(\frac{1}{2}\right)^3 = \frac{1}{8}\end{align*}$	$\begin{align*}2^3=8\end{align*}$
  2	$\begin{align*}\left(\frac{1}{2}\right)^2 = \frac{1}{4}\end{align*}$	$\begin{align*}2^2=4\end{align*}$
  1	$\begin{align*}\left(\frac{1}{2}\right)^1 = \frac{1}{2}\end{align*}$	$\begin{align*}2^1=2\end{align*}$
  0	$\begin{align*}\left(\frac{1}{2}\right)^0 = 1\end{align*}$	$\begin{align*}2^0=1\end{align*}$
  -1	$\begin{align*}\left(\frac{1}{2}\right)^{-1} = 2\end{align*}$	$\begin{align*}2^{-1}=\frac{1}{2}\end{align*}$
  -2	$\begin{align*}\left(\frac{1}{2}\right)^{-2} = 4\end{align*}$	$\begin{align*}2^{-2}=\frac{1}{4}\end{align*}$
  -3	$\begin{align*}\left(\frac{1}{2}\right)^3 = 8\end{align*}$	$\begin{align*}2^{-3}=\frac{1}{8}\end{align*}$

  播放段落

  Notice that $\begin{align*}y=\left(\frac{1}{2}\right)^x\end{align*}$ is a reflection over the $\begin{align*}y\end{align*}$ -axis of $\begin{align*}y=2^x\end{align*}$ . Therefore , instead of , the function $\begin{align*}y=\left(\frac{1}{2}\right)^x\end{align*}$ decreases exponentially, or exponentially decays . Anytime $\begin{align*}b\end{align*}$ is a fraction or decimal between zero and one, the exponential function will decay. And, just like an exponential growth function , and exponential decay function has the form $\begin{align*}y=ab^x\end{align*}$ and $\begin{align*}a>0\end{align*}$ . However, to be a decay function, $\begin{align*}0 < b < 1\end{align*}$ . The exponential decay function also has an asymptote at $\begin{align*}y=0\end{align*}$ .
  ::注意 Y= (12) x 是 Y = 2x 的 Y 轴的反射。 因此, 函数 y = (12) x 将以指数速度递减, 或以指数速度衰减。 任何时间 b 是零到一之间的小数或小数, 指数函数将会衰减。 和指数增长函数一样, 指数衰减函数有 y=abx 和 a> 0 的形状。 但是, 要成为衰变函数, 0 < b < 1 。 指数衰变函数在 y= 0 时也有一个星数 。

  播放段落

  Let's determine which of the following functions are exponential decay functions, exponential growth functions, or neither and briefly explain our answers.
  ::让我们确定以下哪些函数是指数衰变函数、指数增长函数或两者都不是,并简要解释我们的答案。

  播放段落
  1. $\begin{align*}y=4(1.3)^x\end{align*}$
     ::y=4(1.3)x
  播放段落
  2. $\begin{align*}f(x)=3 \left(\frac{6}{5}\right)^x\end{align*}$
     :fx)=3(65)x
  播放段落
  3. $\begin{align*}y = \left(\frac{3}{10}\right)^x\end{align*}$
     ::y= (310) x
  播放段落
  4. $\begin{align*}g(x)= -2(0.65)^x\end{align*}$
     :xx) 2 (0.65)x

  播放段落

  a. and b. are exponential growth functions because $\begin{align*}b>1\end{align*}$ .
  ::a.和b.是指数增长函数,因为 b>1。

  播放段落

  c. is an exponential decay function because $\begin{align*}b\end{align*}$ is between zero and one.
  ::c 是一个指数衰变函数,因为 b 介于零和一之间。

  播放段落

  d. is neither growth or decay because $\begin{align*}a\end{align*}$ is negative.
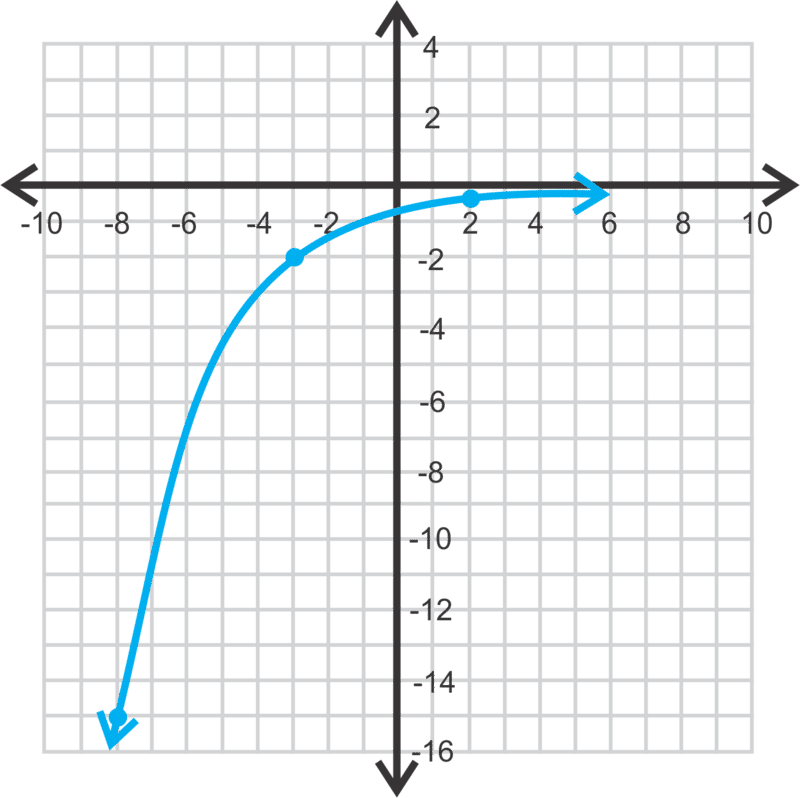
  ::d. 既不是增长,也不是因负值而衰减。

  播放段落

  Let's graph $\begin{align*}g(x)=-2 \left(\frac{2}{3}\right)^{x-1}+1\end{align*}$  and find the $\begin{align*}y\end{align*}$ - intercept , asymptote, domain , and range .
  ::让我们将g(x)\\\\\\\\\\\\\\\\\\\1+1, 并找到 y 界面、 空点、 域名和范围 。

  播放段落

  To graph this function, you can either plug it into your calculator (entered Y= -2(2/3)^(X-1)+1) or graph $\begin{align*}y=-2 \left(\frac{2}{3}\right)^x\end{align*}$ and shift it to the right one unit and up one unit. We will use the second method; final answer is the blue function below.
  ::要图形化此函数, 您可以将它插入到您的计算器( 进入 Y= - 2( 2/3)%( X-1) +1) 或图形 y& 2( 23) x 中, 并移动到右边的一个单位和上一个单位。 我们将使用第二种方法; 最后一个答案是下面的蓝色函数 。

  

  播放段落

  The $\begin{align*}y\end{align*}$ -intercept is:
  ::y 界面是:

  播放段落

  $\begin{align*}y=-2 \left(\frac{2}{3}\right)^{0-1}+1=-2 \cdot \frac{3}{2}+1=-3+1=-2\end{align*}$
  ::y[2](230)-1+1232+1}3+122

  播放段落

  The horizontal asymptote is $\begin{align*}y=1\end{align*}$ , the domain is all real numbers and the range is $\begin{align*}y < 1\end{align*}$ .
  ::水平数为y=1, 域为所有真实数字, 范围为 y < 1 。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find the city's population in 2017 if the population was 10,000 in 2012 and is declining at a rate of 5% each year.
  ::先前,您被要求在2017年寻找城市人口,如果2012年人口为10,000人,并且每年以5%的速度下降。

  播放段落

  This is an example of exponential decay, so we can once again use the exponential form $\begin{align*}f(x)=a \cdot b^{x-h}+k\end{align*}$ , but we have to be careful. In this case, a = 10,000, the starting population, x-h = 5 the number of years, and k = 0, but b is a bit trickier. If the population is decreasing by 5%, each year the population is (1 - 5%) or (1 - 0.05) = 0.95 what it was the previous year. This is our b .
  ::这是一个指数衰减的例子, 所以我们可以再次使用指数表 f( x) = abx-h+k, 但我们必须小心。 在此情况下, a = 10,000, 起始人口, x-h = 5 年数, k = 0, b 则略微小一些。 如果人口减少5%, 人口每年(1 - 5%) 或 (1- 0.05) = 0.95 与前一年一样。 这是我们的 b 。

  播放段落

  $$\begin{align*}P = 10,000 \cdot 0.95^5\\ = 10,000 \cdot 0.7738 = 7738\end{align*}$$
  ::P=100000=100000.0.955=100000=100000=0.7738=7738

  播放段落

  Therefore, the city's population in 2017 is 7,738.
  ::因此,2017年城市人口为7 738人。

  播放段落

  For Examples 2-4, graph the . Find the $\begin{align*}y\end{align*}$ -intercept, asymptote, domain, and range.
  ::示例 2-4 图形 . 查找 y 界面、 空点、 域和范围 。

  播放段落

  Example 2
  ::例2

  播放段落

  $\begin{align*}f(x)=4 \left(\frac{1}{3}\right)^x\end{align*}$
  :xx)=4(13)x

  播放段落

  $\begin{align*}y\end{align*}$ -intercept: $\begin{align*}(4, 0)\end{align*}$ , asymptote: $\begin{align*}y=0\end{align*}$ , domain: all reals, range: $\begin{align*}y < 0\end{align*}$
  ::y 拦截 : (4,0) 停止 : y= 0 , 域 : 所有真数, 范围 : y < 0

  

  播放段落

  Example 3
  ::例3

  播放段落

  $\begin{align*}y=-2 \left(\frac{2}{3}\right)^{x+3}\end{align*}$
  ::y2( 23) x+3

  播放段落

  $\begin{align*}y\end{align*}$ -intercept: $\begin{align*}\left(0, -\frac{16}{27}\right)\end{align*}$ , asymptote: $\begin{align*}y=0\end{align*}$ , domain: all reals, range: $\begin{align*}y<0\end{align*}$
  ::y 截取 : (0, - 1627) , 停止: y= 0, 域: 所有真数, 范围: y < 0

  

  播放段落

  Example 4
  ::例4

  播放段落

  $\begin{align*}g(x)= \left(\frac{3}{5}\right)^x-6\end{align*}$
  ::g(x) = (35)x-6

  播放段落

  $\begin{align*}y\end{align*}$ -intercept: $\begin{align*}(-5, 0)\end{align*}$ , asymptote: $\begin{align*}y=-6\end{align*}$ , domain: all reals, range: $\begin{align*}y>-6\end{align*}$
  ::y- 拦截-5,0) 停止 : y 6, 域 : 所有真数, 范围 : y 6

  

  播放段落

  For Examples 5-8, determine if the functions are exponential growth, exponential decay, or neither.
  ::对于例5-8,确定函数是指数增长、指数衰减还是两者都不是。

  播放段落

  Example 5
  ::例5

  播放段落

  $\begin{align*}y=2.3^x\end{align*}$
  ::y=2.3x y=2.3x

  播放段落

   exponential growth
  ::指数指数增长

  播放段落

  Example 6
  ::例6

  播放段落

  $\begin{align*}y=2 \left(\frac{4}{3}\right)^{-x}\end{align*}$
  ::y=(2(43)-x

  播放段落

  exponential decay; recall that a negative exponent flips whatever is in the base. $\begin{align*}y=2 \left(\frac{4}{3}\right)^{-x}\end{align*}$ is the same as $\begin{align*}y=2 \left(\frac{3}{4} \right)^{x}\end{align*}$ , which looks like our definition of a decay function.
  ::指数衰变; 提醒注意, 负指数翻转会显示基数中的任何内容。 y=2( 43) - x 与y=2( 34)x 相同, 这看起来像我们对衰变函数的定义 。

  播放段落

  Example 7
  ::例7

  播放段落

  $\begin{align*}y=3\cdot 0.9^x\end{align*}$
  ::y=30.9x

  播放段落

  exponential decay
  ::指数衰变

  播放段落

  Example 8
  ::例8

  播放段落

  $\begin{align*}y=\frac{1}{2} \left(\frac{4}{5}\right)^{x}\end{align*}$
  ::y=12( 45)x

  播放段落

  neither; $\begin{align*}a < 0\end{align*}$
  ::都不是; a<0

  播放段落

  Review
  ::回顾

  播放段落

  Determine which of the following functions are exponential growth, exponential decay or neither.
  ::确定以下哪些函数是指数增长、指数衰减或两者都不是。

  播放段落
  1. $\begin{align*}y= -\left(\frac{2}{3}\right)^x\end{align*}$
     ::y y( 23) x
  播放段落
  2. $\begin{align*}y= \left(\frac{4}{3}\right)^x\end{align*}$
     ::y=( 43)x
  播放段落
  3. $\begin{align*}y=5^x\end{align*}$
     ::y=5x y=5x
  播放段落
  4. $\begin{align*}y= \left(\frac{1}{4}\right)^x\end{align*}$
     ::y=( 14) x
  播放段落
  5. $\begin{align*}y= 1.6^x\end{align*}$
     ::y=1.6x y=1.6x
  播放段落
  6. $\begin{align*}y= -\left(\frac{6}{5}\right)^x\end{align*}$
     ::y( 65)x
  播放段落
  7. $\begin{align*}y= 0.99^x\end{align*}$
     ::y=0.99x y=0.99x

  播放段落

  Graph the following exponential functions. Find the $\begin{align*}y\end{align*}$ -intercept, the equation of the asymptote and the domain and range for each function.
  ::图形显示以下的指数函数。查找 y 界面、 空点的方程以及每个函数的域和范围。

  播放段落
  8. $\begin{align*}y= \left(\frac{1}{2}\right)^x\end{align*}$
     ::y=( 12) x
  播放段落
  9. $\begin{align*}y=(0.8)^{x+2}\end{align*}$
     ::y=( 0. 8) x+2
  播放段落
  10. $\begin{align*}y=4 \left(\frac{2}{3}\right)^{x-1}-5\end{align*}$
      ::y=4( 23)x- 1 - 5
  播放段落
  11. $\begin{align*}y= -\left(\frac{5}{7}\right)^x +3\end{align*}$
      ::y* (57x+3)
  播放段落
  12. $\begin{align*}y= \left(\frac{8}{9}\right)^{x+5} -2\end{align*}$
      ::y=( 89x+5-2)
  播放段落
  13. $\begin{align*}y=(0.75)^{x-2}+4\end{align*}$
      ::y=( 0. 75x-2+4)
  播放段落
  14. Is the domain of an exponential function always all real numbers? Why or why not?
      ::指数函数的域是否总是所有真实数字?为什么或为什么不是?
  播放段落
  15. A discount retailer advertises that items will be marked down at a rate of 10% per week until sold. The initial price of one item is $50.
      播放段落
      1. Write an exponential decay function to model the price of the item $\begin{align*}x\end{align*}$ weeks after it is first put on the rack.
         ::写入指数衰减函数, 以模拟项目 x 首次放在架子上之后的周价格 。
      播放段落
      2. What will the price be after the item has been on display for 5 weeks?
         ::5周内展出该物品之后的价格会是多少?
      播放段落
      3. After how many weeks will the item be half its original price?
         ::经过多少周之后,该项目将达到其原价的一半?
      
      ::贴现零售商广告说,在售出之前,物品将按每周10%的费率下标。 一个物品的最初价格是50美元。 写入一个指数衰变函数, 以模拟物品在首次放入架子之后的 x 周的价格。 在物品展出5周之后, 价格会是多少? 在物品的最初价格的一半之后, 多少周的价格是多少?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。