Course: 8.4 数字e | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

编号e

The interest on a sum of money that compounds continuously can be calculated with the formula $\begin{aligned} I = P e^{r t} - P \end{aligned}$ , where P is the amount invested (the principal), r is the interest rate , and t is the amount of time the money is invested. If you invest $1000 in a bank account that pays 2.5% interest compounded continuously and you leave the money in that account for 4 years, how much interest will you earn?
::持续混合的金额的利息可以用公式I=Pert-P计算,P是投资金额(本金 ) , r是利率, t是投资时间。如果您在持续支付2.5%利息的银行账户上投资1 000美元,然后将这笔钱留在该账户4年,你将赚取多少利息?

The Number e
::编号e

There are many special numbers in mathematics: $\begin{aligned} π \end{aligned}$ , zero, $\begin{aligned} \sqrt{2} \end{aligned}$ , among others. In this concept, we will introduce another special number that is known only by a letter, $\begin{aligned} e \end{aligned}$ . It is called the natural number (or base), or the Euler number , named after the Swiss mathematician Leonhard Euler who popularized the use of the letter $\begin{aligned} e \end{aligned}$ for the constant . Credit for discovery of the constant itself goes to another important Swiss mathematician, Jacob Bernoulli, and his study of sequences in compound interest.
::数学中有许多特殊数字:,0,2,等等。在这个概念中,我们将引入另一个只有字母才知道的特殊数字,即称为自然数字(或基准),或以瑞士数学家Leonhard Euler命名的Euler数字。他把字母的使用普及到常数中。发现常数本身的功劳归另一个重要的瑞士数学家Jacob Bernoulli,以及他为了复合利益对序列的研究。

We previously learned that the formula for compound interest is $\begin{aligned} A = P {(1 + \frac{r}{n})}^{n t} \end{aligned}$ . Let’s set $\begin{aligned} P, r \end{aligned}$ and $\begin{aligned} t \end{aligned}$ equal to one and see what happens, $\begin{aligned} A = {(1 + \frac{1}{n})}^{n} \end{aligned}$ .
::我们以前知道复利的公式是 A=P(1+rn)nt。让我们设定 P,r 和 t 等于 1, 看看会发生什么, A=(1+1n)n。

Finding the values of $\begin{aligned} {(1 + \frac{1}{n})}^{n} \end{aligned}$ as $\begin{aligned} n \end{aligned}$ gets larger
::当 n 变大时查找 (1+1n) n 的值

Step 1: Copy the table below and fill in the blanks. Round each entry to the nearest 4 decimal places.
::第1步:复制下表并填入空白。将每个条目四舍五入到小数点后最接近的四位位数。

$\begin{aligned} n \end{aligned}$	1	2	3	4	5	6	7	8
$\begin{aligned} {(1 + \frac{1}{n})}^{n} \end{aligned}$	$\begin{aligned} {(1 + \frac{1}{1})}^{1} = 2 \end{aligned}$	$\begin{aligned} {(1 + \frac{1}{2})}^{2} = 2.25 \end{aligned}$

Step 2: Does it seem like the numbers in the table are approaching a certain value? What do you think the number is?
::第2步:表内的数字似乎接近某个数值吗?你认为数字是什么?

Step 3: Find $\begin{aligned} {(1 + \frac{1}{100})}^{100} \end{aligned}$ and $\begin{aligned} {(1 + \frac{1}{1000})}^{1000} \end{aligned}$ . Does this change your answer from #2?
::第3步:查找(1+1100100)100和(1+111001000)1000。这是否改变了您对 #2的回答?

Step 4: Fill in the blanks: As $\begin{aligned} n \end{aligned}$ approaches ___________, ___________ approaches $\begin{aligned} e \approx 2.718281828459 \dots \end{aligned}$
::第4步:填补空白:随着n接近___, e___________________________________________________________________________________________________________________#___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

We define $\begin{aligned} e \end{aligned}$ as the number that $\begin{aligned} {(1 + \frac{1}{n})}^{n} \end{aligned}$ approaches as $\begin{aligned} n \to \infty \end{aligned}$ ( $\begin{aligned} n \end{aligned}$ approaches infinity). $\begin{aligned} e \end{aligned}$ is an irrational number with the first 12 decimal places above.
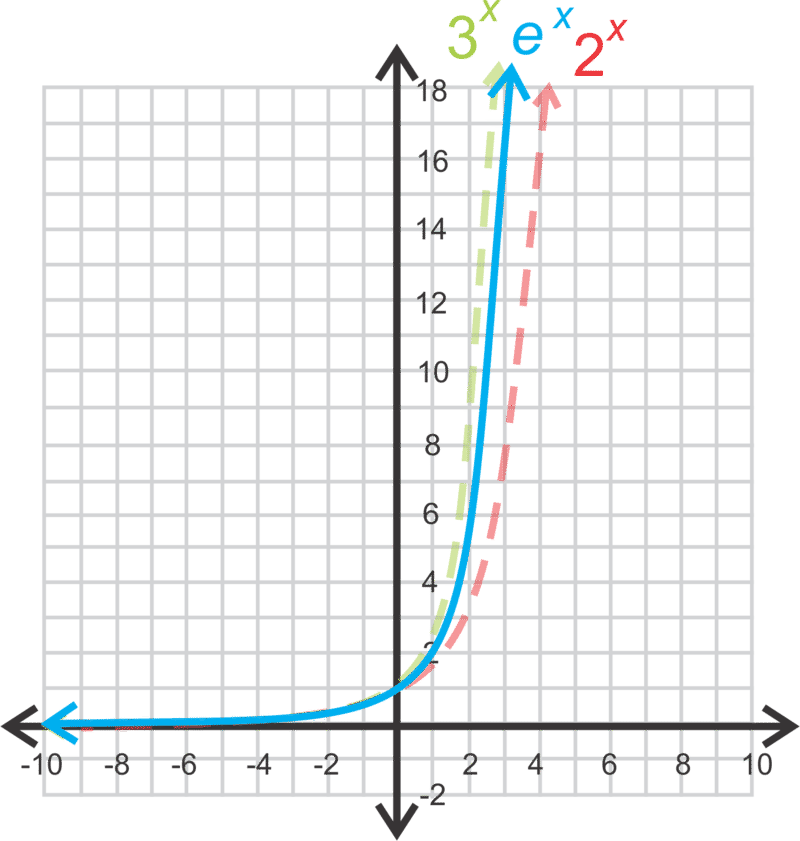
::我们将e定义为(1+1n)n接近n(n接近无穷)。 e 是一个不合理的数字,前一位小数点为12位。

Let's graph $\begin{aligned} y = e^{x} \end{aligned}$ and identify the asymptote , $\begin{aligned} y \end{aligned}$ - intercept , domain and range .
::让我们来绘制 y =ex 并识别无线、 y 界面、域和范围。

As you would expect, the graph of $\begin{aligned} e^{x} \end{aligned}$ will curve between $\begin{aligned} 2^{x} \end{aligned}$ and $\begin{aligned} 3^{x} \end{aligned}$ .
::如您所料前方图将在 2x 和 3x 之间曲线。

The asymptote is $\begin{aligned} y = 0 \end{aligned}$ and the $\begin{aligned} y \end{aligned}$ -intercept is (0, 1) because anything to the zero power is one. The domain is all real numbers and the range is all positive real numbers; $\begin{aligned} y > 0 \end{aligned}$ .
::空点为 y=0, y 拦截是 (0, 1) , 因为任何零功率是 1 。域是所有真实数字, 范围是所有正数 ; y> 0 。

Now, let's simplify $\begin{aligned} e^{2} \cdot e^{4} \end{aligned}$ .
::现在,让我们简化e2e4。

The bases are the same, so you can just add the exponents. The answer is $\begin{aligned} e^{6} \end{aligned}$ .
::基数相同, 所以您可以添加引号。答案是e6 。

Finally, let's solve the following problem.
::最后,让我们解决以下问题。

Gianna opens a savings account with $1000 and it accrues interest continuously at a rate of 5%. What is the balance in the account after 6 years?
::Gianna开立了一个1 000美元的储蓄账户,以5%的利率不断累积利息。 6年后账户的余额是多少?

Previously, the word problems you have dealt with involve interest that compounded monthly, quarterly, annually, etc. In this example, the interest compounds continuously. The equation changes slightly, from $\begin{aligned} A = P {(1 + \frac{r}{n})}^{n t} \end{aligned}$ to $\begin{aligned} A = P e^{r t} \end{aligned}$ , without $\begin{aligned} n \end{aligned}$ , because there is no longer any interval. Therefore , the equation for this problem is $\begin{aligned} A = 1000 e^{0.05 (6)} \end{aligned}$ and the account will have $1349.86 in it. Compare this to daily accrued interest, which would be $\begin{aligned} A = 1000 {(1 + \frac{0.05}{365})}^{365 (6)} = 1349.83 \end{aligned}$ .
::以前,您所处理的单词问题涉及每月、季度、年度等的利息,在这个例子中,利息化合物是连续的。方程式略有变化,从A=P(1+rn)nt到A=Pert,没有n,因为不再有任何间隔。因此,这个问题的方程式是A=1000e0.05(6),账户中将有1349.86美元。与每日累计利息相比,这是A=1000(1+0.05365)365(6)=1349.83。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find how much money you will earn after 4 years.
::更早之前,有人要求你找找四年后能赚到多少钱

Plug the given values into the equation $\begin{aligned} I = P e^{r t} \end{aligned}$ and solve for I.
::将给定值插入方程式 I = Pert, 并为 I 解析。

\begin{aligned} I = P e^{r t} - P \\ I = 1000 \cdot e^{0.025 \cdot 4} - 1000 \\ I = 1000 \cdot e^{0.1} - 1000 \\ I = 1000 \cdot 1.10517 - 1000 \\ I = 1105.17 - 1000 = 105.17 \end{aligned}

::I=Pert-PI=10000-e0.025-4-1000I=10000-e0.1-1000I=10000-e0.1-1000I=10000-11.0517-1000I=11005.17-1000=105.17-1000=105.17

Therefore, at the end of 4 years, you will have earned $105.17 in interest.
::因此,在四年结束时,你将赚取105.17美元的利息。

Determine if Examples 2-5 are , decay, or neither.
::确定例 2-5 是、衰变还是都不是。

Recall to be exponential growth, the base must be greater than one. To be , the base must be between zero and one.
::回顾指数增长,基数必须大于1。基数必须是0到1。基数必须是0到1。

Example 2
::例2

$\begin{aligned} y = \frac{1}{2} e^{x} \end{aligned}$
::y=12ex y=12ex

Exponential growth; $\begin{aligned} e > 1 \end{aligned}$
::指数增长;e>1

Example 3
::例3

$\begin{aligned} y = - 4 e^{x} \end{aligned}$
::y4x

Neither; $\begin{aligned} a < 0 \end{aligned}$
::两者中均无;a<0

Example 4
::例4

$\begin{aligned} y = e^{- x} \end{aligned}$
::y=e-x y=e-x

Exponential decay; $\begin{aligned} e^{- x} = {(\frac{1}{e})}^{x} \end{aligned}$ and $\begin{aligned} 0 < \frac{1}{e} < 1 \end{aligned}$
::指数衰变; e-x=(1e)x 和 0 < 1e < 1

Example 5
::例5

$\begin{aligned} y = 2 {(\frac{1}{e})}^{- x} \end{aligned}$
::y= 2(1e)-x

Exponential growth; $\begin{aligned} {(\frac{1}{e})}^{- x} = e^{x} \end{aligned}$
::指数增长;(1e)-x=ex

Example 6
::例6

Simplify the following expression with $\begin{aligned} e \end{aligned}$ .
::以 e. 简化以下表达式。

$\begin{aligned} 2 e^{- 3} \cdot e^{2} \end{aligned}$
::2 e-3e2

$\begin{aligned} 2 e^{- 3} \cdot e^{2} = 2 e^{- 1} \end{aligned}$ or $\begin{aligned} \frac{2}{e} \end{aligned}$
::2 - 3e2=2e-1或2e

Example 7
::例7

Simplify the following expression with $\begin{aligned} e \end{aligned}$ .
::以 e. 简化以下表达式。

$\begin{aligned} \frac{4 e^{6}}{16 e^{2}} \end{aligned}$
::4 e616e2

$\begin{aligned} \frac{4 e^{6}}{16 e^{2}} = \frac{e^{4}}{4} \end{aligned}$
::4,616e2=e44

Example 8
::例8

The rate of radioactive decay of radium is modeled by $\begin{aligned} R = P e^{- 0.00043 t} \end{aligned}$ , where $\begin{aligned} R \end{aligned}$ is the amount (in grams) of radium present after $\begin{aligned} t \end{aligned}$ years and $\begin{aligned} P \end{aligned}$ is the initial amount (also in grams). If there is 698.9 grams of radium present after 5,000 years, what was the initial amount?
::R=Pe-0.00043t以放射性衰减率为模型,R是年之后的放射性衰减率(克),P是初始值(也以克计),如果5 000年后有698.9克的放射性衰减率,初始值是多少?

Use the formula given in the problem and solve for what you don’t know.
::使用问题中给出的公式解决您不知道的事情。

\begin{aligned} R & = P e^{- 0.00043 t} \\ 698.9 & = P e^{- 0.00043 (5000)} \\ 698.9 & = P (0.11648) \\ 6000 & = P \end{aligned}

::R=Pe-0000043t698.9=Pe-0000043(5000698.9=P(0.116.448)600=P)

There was about 6000 grams of radium to start with.
::开始大约有6000克的放射线。

Review
::回顾

Determine if the following functions are exponential growth, decay or neither. Give a reason for your answer.
::确定以下函数是指数增长、衰变或两者都不是。请说明回答的理由。

$\begin{aligned} y = \frac{4}{3} e^{x} \end{aligned}$
::y=43ex y=43ex

$\begin{aligned} y = - e^{- x} + 3 \end{aligned}$
::ye - x+3

$\begin{aligned} y = {(\frac{1}{e})}^{x} + 2 \end{aligned}$
::y=(1e)x+2

$\begin{aligned} y = {(\frac{3}{e})}^{- x} - 5 \end{aligned}$
::y=( 3e) - x - 5

Simplify the following expressions with $\begin{aligned} e \end{aligned}$ .
::以 e. 简化以下表达式。

$\begin{aligned} e^{- 3} \cdot e^{12} \end{aligned}$
::电子-3e12

$\begin{aligned} \frac{5 e^{- 4}}{e^{3}} \end{aligned}$
::5e-4e3 5e-4e3

$\begin{aligned} 6 e^{5} e^{- 4} \end{aligned}$
::6e5e-4

$\begin{aligned} {(\frac{4 e^{4}}{3 e^{- 2} e^{3}})}^{- 2} \end{aligned}$
:4e43e-2e3)-2(4e43e-2e3)

Solve the following word problems.
::解决以下字词问题。

The population of Springfield is growing exponentially. The growth can be modeled by the function $\begin{aligned} P = I e^{0.055 t} \end{aligned}$ , where $\begin{aligned} P \end{aligned}$ represents the projected population, $\begin{aligned} I \end{aligned}$ represents the current population of 100,000 in 2012 and $\begin{aligned} t \end{aligned}$ represents the number of years after 2012.
::斯普林菲尔德的人口正在成倍增长。增长可以通过P=Ie0.055t的函数进行模拟,P代表预计人口,我代表2012年的目前人口100,000人, t代表2012年之后的年数。

To the nearest person, what will the population be in 2022?
::对最近的一个人来说,2022年的人口将是什么?

In what year will the population double in size if this growth rate continues?
::如果这一增长率继续下去,人口规模将在哪一年翻一番?

The value of Steve’s car decreases in value according to the exponential decay function: $\begin{aligned} V = P e^{- 0.12 t} \end{aligned}$ , where $\begin{aligned} V \end{aligned}$ is the current value of the vehicle, $\begin{aligned} t \end{aligned}$ is the number of years Steve has owned the car and $\begin{aligned} P \end{aligned}$ is the purchase price of the car, $25,000.
::V=Pe-0.12t, V是车辆的现值, t是史蒂夫拥有汽车的年数,P是汽车的购买价格25 000美元。

To the nearest dollar, what will the value of Steve’s car be in 2 years?
::史蒂夫的汽车在两年内的价值会是多少?

To the nearest dollar, what will the value be in 10 years?
::最接近的美元,十年内值是多少?

Naya invests $7500 in an account which accrues interest continuously at a rate of 4.5%.
::Naya投资7500美元在一个账户中,该账户以4.5%的利率持续产生利息。

Write an exponential growth function to model the value of her investment after $\begin{aligned} t \end{aligned}$ years.
::写一个指数增长函数来模拟她投资价值的模型在 T 年之后。

How much interest does Naya earn in the first six months to the nearest dollar?
::纳亚在头6个月中赚到多少利息至最近的美元?

How much money, to the nearest dollar, is in the account after 8 years?
::8年后的账户里有多少钱, 最接近的美元?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

编号e

The Number e ::编号e

Finding the values of ( 1 + 1 n ) n as n gets larger ::当 n 变大时查找 (1+1n) n 的值

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Example 8 ::例8

Review ::回顾

Review (Answers) ::回顾(答复)