Course: 8.7 图形对数函数

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 图形对数函数

Collapse Expand
图形对数函数
Your math homework assignment is to find out which quadrants the graph of the function $\begin{aligned} f (x) = 4 \ln (x + 3) \end{aligned}$ falls in. On the way home, your best friend tells you, "This is the easiest homework assignment ever! All fall in Quadrants I and IV." You're not so sure, so you go home and graph the function as instructed. Your graph falls in Quadrant I as your friend thought, but instead of Quadrant IV, it also falls in Quadrants II and III. Which one of you is correct?
::您的数学作业任务是找出函数 f( x) = 4ln {( x+ 3) 的图形属于哪个四分位数。在回家的路上, 您最好的朋友告诉你, “ 这是有史以来最简单的作业任务! 全部落在 Quadrants I 和 IV 中。” 您不太确定, 因此您可以按指示回家, 绘制函数图。您的图表在 Quadrant I 中依朋友的意想写在 Quadrant I 中, 而不是 Quadrant IV, 它也属于 Qadrant II 和 III 。你们中的哪一个是正确的 ?

Graphing Logarithmic Functions
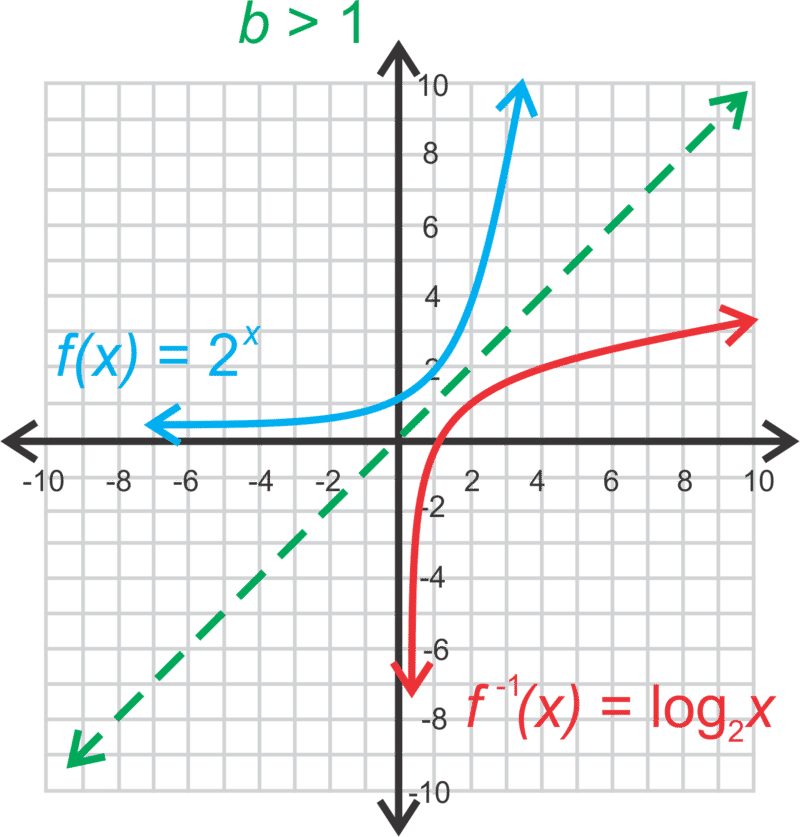
::图形对数函数

Now that we are more comfortable with using these functions as inverses, let’s use this idea to graph a logarithmic function. Recall that functions are inverses of each other when they are mirror images over the line $\begin{aligned} y = x \end{aligned}$ . Therefore, if we reflect $\begin{aligned} y = b^{x} \end{aligned}$ over $\begin{aligned} y = x \end{aligned}$ , then we will get the graph of $\begin{aligned} y = \log_{b} x \end{aligned}$ .
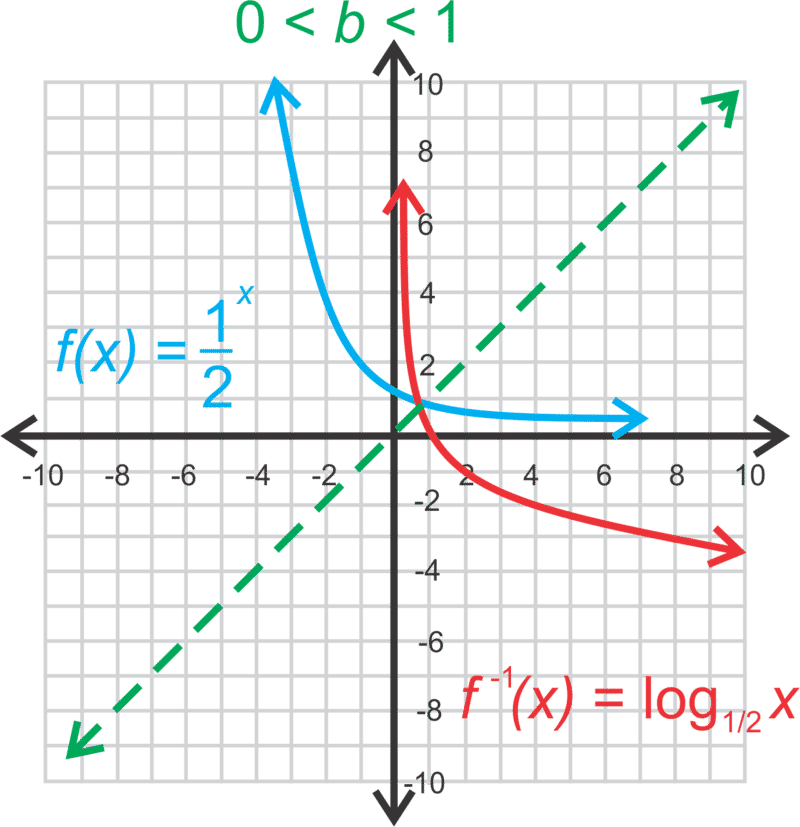
::现在,我们更愿意使用这些函数作为反函数,让我们使用这个想法来绘制对数函数。当函数是 y=x 线上的镜像图像时,提醒注意这些函数是彼此的反函数。因此,如果我们在 y=x 上反射 y=bx,那么我们就会得到 y=logbx 的图。

Recall that an exponential function has a horizontal asymptote. Because the logarithm is its inverse, it will have a vertical asymptote. The general form of a logarithmic function is $\begin{aligned} f (x) = a \log_{b} (x - h) + k \end{aligned}$ and the vertical asymptote is $\begin{aligned} x = h \end{aligned}$ . The domain is $\begin{aligned} x > h \end{aligned}$ and the range is all real numbers. Lastly, if $\begin{aligned} b > 1 \end{aligned}$ , the graph moves up to the right. If $\begin{aligned} 0 < b < 1 \end{aligned}$ , the graph moves down to the right.
::提醒注意一个指数函数有一个水平的单点。由于对数是它的反向, 它将有一个垂直的单点。对数函数的一般形式是 f( x) =alogb( x-h)+k, 垂直的对数函数一般形式是 x=h。域是 x>h, 范围是全部真实数字。最后, 如果 b>1, 图形会向右移动。如果 0 < b < 1, 图形会向右移动。

Let's graph $\begin{aligned} y = \log_{3} (x - 4) \end{aligned}$ and state the domain and range.
::让我们用图y=log3}(x- 4)来说明域和范围。

To graph a logarithmic function without a calculator, start by drawing the vertical asymptote, at $\begin{aligned} x = 4 \end{aligned}$ . We know the graph is going to have the general shape of the first function above. Plot a few points, such as (5, 0), (7, 1), and (13, 2) and connect.
::要绘制一个没有计算器的对数函数,首先在 x=4 处绘制垂直静态。我们知道该图将具有上面第一个函数的一般形状。绘制几个点, 如 (5, 0, 7, 1) 和 (13, 2) , 并连接。

The domain is $\begin{aligned} x > 4 \end{aligned}$ and the range is all real numbers.
::域为 x>4, 范围为所有实际数字。

Now, let's determine if (16, 1) is on $\begin{aligned} y = \log (x - 6) \end{aligned}$ .
::现在,让我们确定是否在y=log(x-6)上(16,1)。

Plug in the point to the equation to see if it holds true.
::插在方程的点上看看它是否真实。

$\begin{aligned} 1 & = \log (16 - 6) \\ 1 & = \log 10 \\ 1 & = 1 \end{aligned}$

::1=log(16-6)1=log101=1

Yes, this is true, so (16, 1) is on the graph.
::是的,这是真的,所以图上是16,1。

Finally, let's graph $\begin{aligned} f (x) = 2 \ln (x + 1) \end{aligned}$ .
::最后,让我们用图表f(x)=2ln(x+1)

To graph a natural log, we can use a graphing calculator. Press $\begin{aligned} Y = \end{aligned}$ and enter in the function, $\begin{aligned} Y = 2 \ln (x + 1) \end{aligned}$ , GRAPH .
::要绘制自然日志图, 我们可以使用图形计算器。按 Y = 并输入此函数, Y= 2ln( x+1), GRAPH 。

Examples
::实例

Example 1
::例1

Earlier, you were asked to determine if your friend was correct.
::早些时候,有人要求你确定你的朋友是否正确。

The vertical asymptote of the function $\begin{aligned} f (x) = 4 \ln (x + 3) \end{aligned}$ is $\begin{aligned} x = - 3 \end{aligned}$ . Since x will approach $\begin{aligned} - 3 \end{aligned}$ but never quite reach it, x can assume some negative values. Hence, the function will fall in Quadrants II and III. Therefore, you are correct and your friend is wrong.
::函数 f( x) = 4ln( x+3) 的垂直位数为 x @ 3。由于 x 将接近 - 3, 但无法到达它, x 可以假定一些负值。因此, 该函数将降为二次和三次。因此, 您是正确的, 您的朋友错了。

Example 2
::例2

Graph $\begin{aligned} y = \log_{\frac{1}{4}} x + 2 \end{aligned}$ in an appropriate window.
::图y=log14x+2 在适当的窗口中。

First, there is a vertical asymptote at $\begin{aligned} x = 0 \end{aligned}$ . Now, determine a few easy points, points where the log is easy to find; such as (1, 2), (4, 1), (8, 0.5), and (16, 0).
::首先, x=0 时有一个垂直断点。现在, 确定几个简单点, 日志容易找到的点。例如 (1, 2, 4, 1), (8, 0. 5) 和 (16, 0) 。

To graph a logarithmic function using a TI-83/84, enter the function into $\begin{aligned} Y = \end{aligned}$ and use the Formula: $\begin{aligned} l o g_{a} x = \frac{l o g_{b} x}{l o g_{b} a} \end{aligned}$ . The keystrokes would be:
::要用 TI-83/84 绘制对数函数,请将函数输入 Y= ,并使用公式: logbxlogba : logax= logblogba。键对数将是:

$\begin{aligned} Y = \frac{\log (x)}{\log (\frac{1}{4})} + 2 \end{aligned}$ , GRAPH
::Y=log(x)log(14)+2,GRAPH

To see a table of values, press $\begin{aligned} 2^{n d} \to \end{aligned}$ GRAPH .
::要查看数值表,请按2ndGRAPH。

Example 3
::例3

Graph $\begin{aligned} y = - \log x \end{aligned}$ using a graphing calculator. Find the domain and range.
::使用图形计算器的 ylogx 图形。查找域和范围。

The keystrokes are $\begin{aligned} Y = - \log (x) \end{aligned}$ , GRAPH .
::键盘是Ylog(x),GRAPH。

The domain is $\begin{aligned} x > 0 \end{aligned}$ and the range is all real numbers.
::域为 x>0, 区域为所有实际数字。

Example 4
::例4

Is (-2, 1) on the graph of $\begin{aligned} f (x) = \log_{\frac{1}{2}} (x + 4) \end{aligned}$ ?
::f( x) =log12 ( x+4) 的图形是否( 2, 1) ?

Plug (-2, 1) into $\begin{aligned} f (x) = \log_{\frac{1}{2}} (x + 4) \end{aligned}$ to see if the equation holds true.
::插件 (-2, 1) 插入 f( x) = log12 ( x+ 4) , 看看方程式是否正确。

$\begin{aligned} 1 & = \log_{\frac{1}{2}} (- 2 + 4) \\ 1 & = \log_{\frac{1}{2}} 2 \\ 1 & \neq - 1 \end{aligned}$

::1=log12(-2+4)1=log12211

Therefore, (-2, 1) is not on the graph. However, (-2, -1) is.
::因此,(-2,1)没有出现在图表中,但(-2,1)没有出现在图表中。

Review
::回顾

Graph the following logarithmic functions without using a calculator. State the equation of the asymptote, the domain and the range of each function.
::如下的对数函数图解,不使用计算器。请说明无线方程式的方程、域和每个函数的范围。

$\begin{aligned} y = \log_{5} x \end{aligned}$
::y=log5x

$\begin{aligned} y = \log_{2} (x + 1) \end{aligned}$
::y=log2( x+1)

$\begin{aligned} y = \log (x) - 4 \end{aligned}$
::y=log(x)- 4

$\begin{aligned} y = \log_{\frac{1}{3}} (x - 1) + 3 \end{aligned}$
::y=log13(x- 1)+3

$\begin{aligned} y = - \log_{\frac{1}{2}} (x + 3) - 5 \end{aligned}$
::ylog12( x+3) - 5

$\begin{aligned} y = \log_{4} (2 - x) + 2 \end{aligned}$
::y=log4( 2- x)+2

Graph the following logarithmic functions using your graphing calculator.
::用您的图形计算计算器绘制对数函数之后的对数函数。

$\begin{aligned} y = \ln (x + 6) - 1 \end{aligned}$
::y=ln( x+6)- 1

$\begin{aligned} y = - \ln (x - 1) + 2 \end{aligned}$
::yln(x- 1)+2

$\begin{aligned} y = \log (1 - x) + 3 \end{aligned}$
::y=log( 1- x)+3

$\begin{aligned} y = \log (x + 2) - 4 \end{aligned}$
::y=log( x+2) - 4

How would you graph $\begin{aligned} y = \log_{4} x \end{aligned}$ on the graphing calculator? Graph the function.
::您如何在图形化计算器上绘制 y=log4x 的图形? 图形化函数。

Graph $\begin{aligned} y = \log_{\frac{3}{4}} x \end{aligned}$ on the graphing calculator.
::图解计算器上的 y=log34x。

Is (3, 8) on the graph of $\begin{aligned} y = \log_{3} (2 x - 3) + 7 \end{aligned}$ ?
::y=log3&(2x-3)+7的图中是否(3,8)?

Is (9, -2) on the graph of $\begin{aligned} y = \log_{\frac{1}{4}} (x - 5) \end{aligned}$ ?
::y=log14(x-5)的图表上是否(9,2)?

Is (4, 5) on the graph of $\begin{aligned} y = 5 \log_{2} (8 - x) \end{aligned}$ ?
::y=5log2(8-x)的图上是否有(4,5)?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

图形对数函数

Graphing Logarithmic Functions ::图形对数函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Graphing Logarithmic Functions
::图形对数函数

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)