课程： 2.5 水平和垂直单数

章节大纲

选择节常规

折叠展开
常规

全部折叠展开全部
- 选择活动新闻通告
  
  新闻通告讨论区
选择节水平和垂直单数

折叠展开
水平和垂直单数
Rational functions abound in real life, we just don't always think of them that way. For example, suppose you are buying ice cream for you and your friends:
::在现实生活中,理性的功能很多,我们只是不总是这样看待它们。例如,假设你为你和你的朋友买冰淇淋:

The ice cream shop has a deal going, if you buy one cone for $3, then additional cones are only $2.50 each. As you buy more and more cones (more and more lucky friends!), what is the average cost per cone?
::冰淇淋店有一个交易进行中,如果你以3美元买一个锥子,那么额外的锥子每颗只有2.50美元。随着你购买越来越多的锥子(越来越多的幸运朋友! ) , 每锥子的平均成本是多少?

This question can be solved with: $\begin{aligned} P (c) = \frac{(2.5 c + 3)}{c} \end{aligned}$ , where P(c) is price per cone based on number purchased, and c is the number of cones.
::P(c)=(2.5c+3)c,其中P(c)是按购买数量计算的每锥体价格,c是锥体数量。

If you graph this function on a graphing calculator, it is interesting to note the horizontal asymptote at 2.5. What does this represent?
::如果您在图形计算计算器上图形显示此函数, 有趣的是注意2.5的水平零点。这代表什么 ?

How might this process apply to movie tickets, where the first is $12, and each additional is $9? Does this graph also have an asymptote ? What does it represent?
::这个过程如何适用于电影票? 第一个是12美元,每个额外是9美元?这个图是否也有一个零点?它代表什么?

Determining Horizontal and Vertical Asymptotes
::确定水平和垂直单数

Horizontal and Vertical Asymptotes
::水平和垂直单数

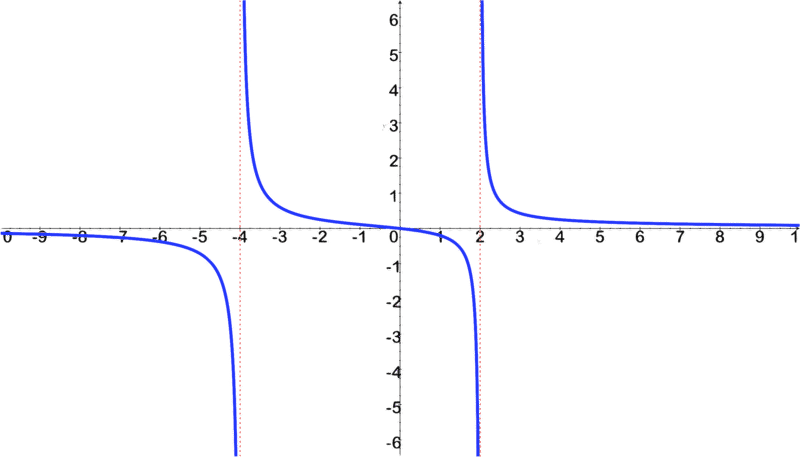
An asymptote is a line or curve to which a function's graph draws closer without touching it. Functions cannot cross a vertical asymptote, and they usually approach horizontal asymptotes in their end behavior (i.e. as $\begin{aligned} x \to \pm \infty \end{aligned}$ ).
::线条或曲线是函数的图形不触碰该线或曲线所接近的线或曲线。函数无法跨过垂直的线或曲线,而函数通常在最终行为中接近水平的线或曲线(如 x) 。

Looking at the graph of $\begin{aligned} f (x) = \frac{x + 2}{(x - 1) (x + 3)} \end{aligned}$ , you will notice that it has two vertical asymptotes (the vertical dotted lines), one is at $\begin{aligned} x = 1 \end{aligned}$ and the other is at $\begin{aligned} x = - 3 \end{aligned}$ .
::查看 f( x) =x+2( 2) x-1( x+3) 的图形时, 您会注意到它有两个垂直的静态( 垂直点线) , 一个在 x=1 , 另一个在 x @% 3 。

Finding a Vertical Asymptote
::查找垂直时点

We can find by simply equating the denominator to zero and then solving for $\begin{aligned} x \end{aligned}$ . In other words, if
::我们可以简单地将分母等同为零,然后解决x。换句话说,如果

$\begin{aligned} f (x) = \frac{P (x)}{Q (x)} \end{aligned}$

:fx)=P(x)Q(x)

Then setting $\begin{aligned} Q (x) = 0 \end{aligned}$ , will give the vertical asymptote(s).
::然后设定 Q( x) =0, 将会给出垂直的空位。

So if
::如果

$\begin{aligned} f (x) = \frac{x + 2}{(x - 1) (x + 3)} \end{aligned}$

:xx) =x+2(x-1)(x+3)

setting
::设置设置设置设置设置设置设置设置设置

$\begin{aligned} (x - 1) (x + 3) = 0 \end{aligned}$

:x-1)(x+3)=0

gives the vertical asymptotes at $\begin{aligned} x = 1 \end{aligned}$ and $\begin{aligned} x = - 3 \end{aligned}$ .
::给定 x=1 和 x3 的垂直小数。

Finding a Horizontal Asymptote
::寻找水平同步状态

Put the rational function in a standard form . That is, expand the numerator and denominator if they are written in a factored form .
::将理性函数设置为标准格式。也就是说,如果分子和分母以系数格式写成,则扩展该分子和分母。

Remove all terms except the terms that contain the largest exponents of $\begin{aligned} x \end{aligned}$ in the numerator and the denominator.
::除含有分子和分母中 x 的最大指数的术语外,删除所有术语。

There are three possibilities:
::有三种可能性:

If the degree of the numerator is smaller than the degree of the denominator, then the horizontal asymptote crosses the $\begin{aligned} y - \end{aligned}$ axis at $\begin{aligned} y = 0 \end{aligned}$ . That is, it is the $\begin{aligned} x - \end{aligned}$ axis itself.
::如果分子的大小小于分母的分母的分量,那么水平的单点横跨y - 轴在y=0。也就是说,它就是 x - 轴本身。

If the degree of the denominator and the numerator are the same , then the horizontal asymptote equals to the ratio of the leading coefficients.
::如果分母和分子的大小相同,则水平零数等于主要系数的比率。

If the degree of the numerator is larger than the degree of the denominator, then there is no horizontal asymptote.
::如果分子的大小大于分母的分母的大小,则没有水平的零星。

Examples
::实例

Example 1
::例1

Earlier, you were asked a question about the movie tickets.
::早些时候,有人问过你关于电影票的问题。

The first question asked the meaning of the horizontal asymptote at 2.5 on the graph of $\begin{aligned} (2.5 c + 3) / c \end{aligned}$ (the cost per cone if the first is $3 and each additional is only $2.50). That asymptote represents the minimum cost per cone, as the number of cones purchased increases. The more cones you buy, the closer the cost of each approaches $2.50, because the additional $0.50 of the initial cone is "shared" among more purchases!
::第一个问题问到(2.5c+3)/c(如果第一个为3美元,而每个额外为2.50美元,则每个锥体的成本为每个锥体的费用为每锥体的最低成本,因为购买的锥体数量增加。购买的锥体越多,每锥体的成本越接近2.5美元,每锥体的成本就越接近2.50美元,因为最初锥体增加的0.50美元在更多的购买中“分摊 ” !

Example 2
::例2

Find the vertical and of
::查找垂直和

$\begin{aligned} f (x) = \frac{2 x^{3} - 2 x^{2} + 5}{3 x^{3} - 81} \end{aligned}$

:x)=2x3-2x2+53x3-81)

To find the vertical asymptote(s), set the denominator to zero and then solve for $\begin{aligned} x \end{aligned}$ .
::要找到垂直的单点, 请将分母设为零, 然后解析 x 。

$\begin{aligned} 3 x^{3} - 81 & = 0 \\ 3 x^{3} & = 81 \\ x^{3} & = 27 \\ x & = \sqrt[3]{27} \\ x & = 3 \end{aligned}$

::3x3- 81=03x3=81x3=27x=273x=3

Thus the graph has a vertical asymptote at $\begin{aligned} x = 3 \end{aligned}$ .
::因此,该图在 x=3 时有一个垂直空位。

To find the horizontal asymptote, we follow the procedure above. Both the numerator and denominator are already written in standard form. Next, remove all terms except the largest exponents of $\begin{aligned} x \end{aligned}$ that are found in the numerator and the denominator:
::要找到水平单点, 我们遵循上面的程序。分子和分母都已经以标准格式写入。接下来, 除在分子和分母中找到的 x 的最大指数外, 删除所有术语 :

$\begin{aligned} \frac{2 x^{3}}{3 x^{3}} \end{aligned}$

::2x33x3

Notice that the degree of the numerator and the denominator are the same and therefore the horizontal asymptote is the ratio of the coefficients,
::注意分子和分母的程度相同,因此水平零点为系数之比,

$\begin{aligned} \frac{2 x^{3}}{3 x^{3}} = \frac{2}{3} \end{aligned}$

::2x33x3=23

So the horizontal asymptote is at $\begin{aligned} y = \frac{2}{3} \end{aligned}$ .
::所以水平的静态是 y=23 。

Example 3
::例3

Find the asymptotes of
::查找

$\begin{aligned} f (x) = \frac{3 x - 2}{2 x^{4} - 9} \end{aligned}$

:xx)=3x-22x4-9)

Remove all terms except the leading terms,
::除前导词外,删除所有术语,

$\begin{aligned} \frac{3 x}{2 x^{4}} \end{aligned}$

::3x2x4

Notice that the degree of the numerator is less than the degree of the denominator. Therefore, the horizontal asymptote is at $\begin{aligned} y = 0 \end{aligned}$ , i.e., the $\begin{aligned} x - \end{aligned}$ axis plays the role of the horizontal asymptote. To find the vertical asymptote, set the denominator equal to zero and solve:
::注意分子的程度小于分母的程度。因此, 水平的负数为y=0, 也就是说, x - 轴发挥水平的负数的作用。要找到垂直的负数, 请将分数设为零并解析 :

$\begin{aligned} 2 x^{4} - 9 & = 0 \\ x^{4} & = \frac{9}{4} \\ x & = \pm \frac{\sqrt{6}}{2} \end{aligned}$

::2x4-9=0x4=94x62

Example 4
::例4

What is the average price of movie tickets, where the first is $12, and each additional is $9, as more and more tickets are purchased?
::电影票的平均价格是多少? 第一张是12美元,每张是9美元,因为购买的票越来越多。

This question is very similar to the one in the introduction. It can be solved with: $\begin{aligned} P (t) = (9 t + 12) / t \end{aligned}$ , where P(t) is price per ticket based on number purchased, and t is the number of tickets.
::这个问题与导言中的问题非常相似,可以用P(t)=(9t+12)/t来解决,P(t)是根据购买的票数计算的每张票的价格,t是票数。

Graphing this on a technological tool, we see a horizontal asymptote at 9, representing the price that each ticket approaches as more and more people (or tickets) share the additional cost of the first ticket. Note that if you were actually buying $\begin{aligned} \infty \end{aligned}$ tickets, the price per ticket would mathematically be $9 per ticket!
::在技术工具上绘制这个图时,我们看到一个水平零点为9的零点,它代表着每张罚单作为越来越多的人(或罚单)所接近的价格。请注意,如果你实际购买了每张罚单,那么每张罚单的价格在数学上是每张罚单的9美元!

Example 5
::例5

Graph
::图图图图图图图

$\begin{aligned} g (x) = \frac{2 x^{2} + 1}{2 x^{2} - 3 x} \end{aligned}$

::g(x) = 2x2+12x2 - 3x

The domain of $\begin{aligned} g \end{aligned}$ is the set of all real numbers except 0 and $\begin{aligned} \frac{3}{2} \end{aligned}$ , that is $\begin{aligned} {x | x \neq 0 and x \neq \frac{3}{2}} \end{aligned}$ . The $\begin{aligned} y - \end{aligned}$ intercept is
$\begin{aligned} y = g (0) = \frac{1}{0} = undefined \end{aligned}$
this tells us that there is no $\begin{aligned} y - \end{aligned}$ intercept. The $\begin{aligned} x - \end{aligned}$ intercept can be found by setting the numerator to zero,
$\begin{aligned} 2 x^{2} + 1 & = 0 \\ 2 x^{2} & = - 1 \\ x^{2} & = \frac{- 1}{2} \\ x & = \sqrt{\frac{- 1}{2}} \end{aligned}$
Notice that this equation has no real solution and therefore, there is no $\begin{aligned} x - \end{aligned}$ intercept either.
::g 域是除 0 和 32 之外所有真实数字的一组, 即 {xx0 和 x32} 。 y- interception isy= g( 0) = 10= 未定义这告诉我们不存在 y- interception。通过将分子设置为 0 2x2+1= 02x2}1x2}1x2}\\\\ 12x\\\\\\\\\\ 12notice , 这个方程式没有真正的解决方案, 因此也没有 x- interception 。

The vertical asymptote can be found by setting the denominator to zero,
$\begin{aligned} 2 x^{2} - 3 x & = 0 \\ x (2 x - 3) & = 0 \end{aligned}$
The two solutions are $\begin{aligned} x = 0 \end{aligned}$ and $\begin{aligned} x = \frac{3}{2} \end{aligned}$ , and these are the vertical asymptotes.
::将分母设定为 0 2x2-3x= 0x(2x-3)=0, 就可以找到垂直静态。两个溶液是 x=0 和 x= 32, 它们是垂直静态。

Finally, the horizontal asymptote is found by analyzing the leading terms:
$\begin{aligned} \frac{2 x^{2} + 1}{2 x^{2} - 3 x} \to \frac{2 x^{2}}{2 x^{2}} = 1 \end{aligned}$
That is, $\begin{aligned} y = 1 \end{aligned}$ is a horizontal asymptote. Again after substituting in some points, we can sketch the graph of $\begin{aligned} g (x) \end{aligned}$ below.
::最后,通过分析前导术语: 2x2+12x2- 3x%2x22x2=1, 即, y=1 是一个水平单数。在替换某些点后, 我们可以绘制下面 g(x) 的图形。

Example 6
::例6

Graph
::图图图图图图图

$\begin{aligned} T (x) = \frac{2 x + 1}{x - 1} \end{aligned}$

::T(x) = 2x+1x-1

Note that the domain of $\begin{aligned} T \end{aligned}$ is the set of all real numbers except 1, that is $\begin{aligned} x \neq 1 \end{aligned}$ . This tells us that the line $\begin{aligned} x = 1 \end{aligned}$ is a vertical asymptote of $\begin{aligned} T (x) \end{aligned}$ . To graph $\begin{aligned} T \end{aligned}$ , there are four important items that you need to find: The $\begin{aligned} y - \end{aligned}$ intercept, the $\begin{aligned} x - \end{aligned}$ intercept, the vertical asymptote and the horizontal asymptote.
::请注意, T 的域是所有真实数字的集合, 除了 1 , 也就是 x\\\\ 1 。这告诉我们, 直线 x= 1 是 T (x) 的垂直等同点。图 T , 您需要找到四个重要项 : y - intercept、 x - intercept、垂直等同点和水平等同点。

The $\begin{aligned} y - \end{aligned}$ intercept can be found by finding $\begin{aligned} y = T (0) \end{aligned}$ .
$\begin{aligned} y = T (0) = \frac{2 (0) + 1}{0 - 1} = - 1 \end{aligned}$
Thus the $\begin{aligned} y - \end{aligned}$ intercept is at point (0, -1).
::y- interfict 可以通过查找 y= T( 0.y= T( 0) =2( 0) + 10- 1\\\\\\ 1 来找到 y- interfict。 y- intervict 是在点 ( 0, - 1) 。

The $\begin{aligned} x - \end{aligned}$ intercept can be found by setting $\begin{aligned} y = T (x) = 0 \end{aligned}$ .
$\begin{aligned} \frac{2 x + 1}{x - 1} = 0 \end{aligned}$
Note that a fraction $\begin{aligned} \frac{a}{b} = 0 \end{aligned}$ if and only if $\begin{aligned} a = 0 \end{aligned}$ , so we can set the numerator of $\begin{aligned} T 9 \end{aligned}$ solve
$\begin{aligned} 2 x + 1 & = 0 \\ x & = \frac{- 1}{2} \end{aligned}$
Notice that we could have just set the numerator to zero and found the $\begin{aligned} x - \end{aligned}$ intercept. In general, set $\begin{aligned} P (x) = 0 \end{aligned}$ to find the $\begin{aligned} x - \end{aligned}$ intercept for any rational function. BUT, you must make sure that the $\begin{aligned} x - \end{aligned}$ value you find is still defined for the function. If both $\begin{aligned} P (x) = 0 \end{aligned}$ and $\begin{aligned} Q (x) = 0 \end{aligned}$ for some value of $\begin{aligned} x \end{aligned}$ then the graph has a hole in it.
::可以通过设置 y= T( x) = 0.2x+1x- 1=0 来找到 x- interception 。但是, 您必须确保您找到的 x- value 仍然为函数定义。如果有 a=0 , 那么我们可以设置 T9 suis2x+1 = 0x\\\\ 12notice 的分子, 这样我们就可以将分子设置为零, 并找到 x- interception 。一般来说, 设置 P( x)=0 来查找 x- interception 的任何合理函数。但是, 您必须确保您找到的 x- value 仍然为函数定义。如果有 x ( x) = 0 和 Q ( x) =0 的数值, 那么图中就会有一个空洞。

Next, the vertical asymptote. Set $\begin{aligned} Q (x) = 0 \end{aligned}$ :
$\begin{aligned} x - 1 & = 0 \\ x & = 1 \end{aligned}$
and the horizontal asymptote:
$\begin{aligned} \frac{2 x + 1}{x - 1} \to \frac{2 x}{x} = 2 \end{aligned}$
Therefore, the vertical asymptote is at $\begin{aligned} x = 1 \end{aligned}$ and the horizontal asymptote is at $\begin{aligned} y = 2 \end{aligned}$ . From this information, we can make the graph shown below.
::下一个是垂直的单点。设置 Q( x) = 0: x-1=0x=1 和水平的单点 : 2x+1x- 1x- 1xx-2xx=2。因此, 垂直的单点在 x=1 , 水平的单点在 y=2 。在此信息中, 我们可以绘制下图。

Review
::回顾

What is the definition of an asymptote?
::" 零星 " 的定义是什么?

Which asymptote direction can a function not cross?
::函数无法交叉的状态方向 ?

Identify the points of discontinuity, holes, vertical asymptotes, x-intercepts and horizontal asymptote of each.
::确定每个点的不连续点、洞点、垂直空洞点、 x 界面点和水平空点。

$\begin{aligned} f (x) = \frac{1}{3 x^{2} + 3 x - 18} \end{aligned}$
:xx)=13x2+3x-18)

$\begin{aligned} f (x) = \frac{x - 2}{x - 4} \end{aligned}$
:xx)=x-2x-4)

$\begin{aligned} f (x) = \frac{x^{3} - x^{2} - 6 x}{- 3 x^{2} - 3 x + 18} \end{aligned}$
:x) =x3 - x2 - 6x - 3x2 - 3x+18

$\begin{aligned} f (x) = \frac{x^{2} + x - 6}{- 4 x^{2} - 16 x - 12} \end{aligned}$
:x) =x2+x-6-4x2-16x-12

Identify the points of discontinuity, holes, vertical asymptotes, and horizontal asymptote of each. Then sketch the graph.
::识别不连续点、孔、垂直零点和水平零点。然后绘制图表。

$\begin{aligned} f (x) = \frac{4}{x^{2} - 3 x} \end{aligned}$
:xx)=4x2-3xx

$\begin{aligned} f (x) = \frac{x - 4}{- 4 x - 16} \end{aligned}$
:xx) =x-4-4-4x-16)

$\begin{aligned} f (x) = \frac{x + 4}{- 2 x - 6} \end{aligned}$
:xx) =x+4-2x-6

$\begin{aligned} f (x) = \frac{x^{3} - 9 x}{3 x^{2} - 6 x - 9} \end{aligned}$
:x) =x3- 9x3x2- 6x- 9

$\begin{aligned} f (x) = \frac{3 x^{2} - 12 x}{x^{2} - 2 x - 3} \end{aligned}$
:xx) = 3x2 - 12xx2 - 2x-3

$\begin{aligned} f (x) = \frac{x^{3} - 16 x}{- 4 x^{2} + 4 x + 24} \end{aligned}$
:x) =x3- 16x-4x2+4x+24

$\begin{aligned} f (x) = \frac{x^{2} + 2 x}{- 4 x + 8} \end{aligned}$
:xx) =x2+2x-4x+8

$\begin{aligned} f (x) = \frac{x + 2}{2 x + 6} \end{aligned}$
:xx) =x+22x+6

$\begin{aligned} f (x) = \frac{2 x^{2} + 10 x + 12}{x^{2} + 3 x + 2} \end{aligned}$
::f(x) = 2x2+10x+12x2+3x+2

$\begin{aligned} f (x) = \frac{3}{x - 2} \end{aligned}$
:xx)=3x-2)

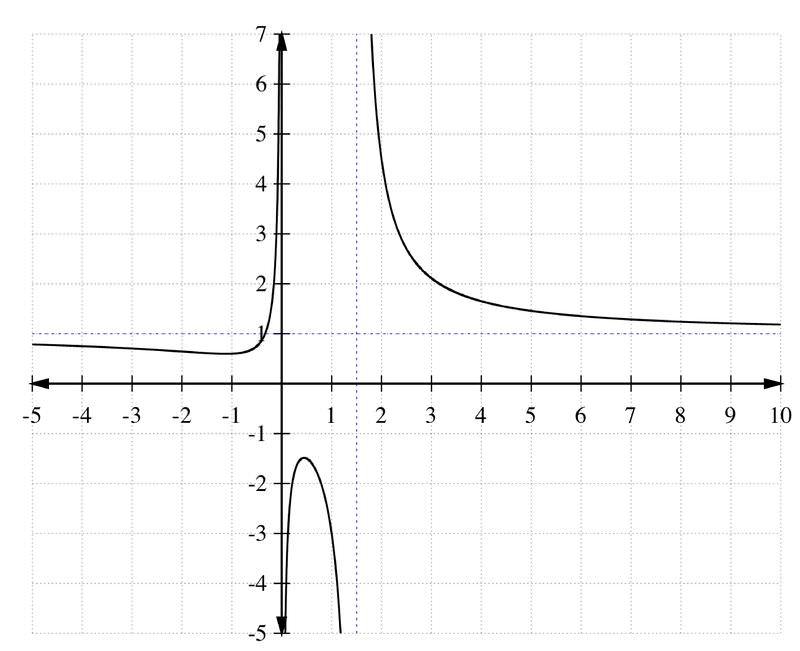
The graph of a rational function is shown below:
::合理函数图如下:

Use the graph to answer the following questions:
::使用图解回答下列问题:

as $\begin{aligned} x \to \infty \end{aligned}$ what does $\begin{aligned} y \end{aligned}$ approach?
::以 x+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

as $\begin{aligned} x \to - \infty \end{aligned}$ what does $\begin{aligned} y \end{aligned}$ approach?
::以 x+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

as $\begin{aligned} x \to 2^{+} \end{aligned}$ what does $\begin{aligned} y \end{aligned}$ approach?
::x% 2+ y 接近什么 ?

as $\begin{aligned} x \to - 4^{-} \end{aligned}$ what does $\begin{aligned} y \end{aligned}$ approach?
::x4 - y 接近什么 ?

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

章节大纲

常规

水平和垂直单数

Determining Horizontal and Vertical Asymptotes ::确定水平和垂直单数

Horizontal and Vertical Asymptotes ::水平和垂直单数

Finding a Vertical Asymptote ::查找垂直时点

Finding a Horizontal Asymptote ::寻找水平同步状态

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)

Determining Horizontal and Vertical Asymptotes
::确定水平和垂直单数

Horizontal and Vertical Asymptotes
::水平和垂直单数

Finding a Vertical Asymptote
::查找垂直时点

Finding a Horizontal Asymptote
::寻找水平同步状态

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Review
::回顾

Review (Answers)
::回顾(答复)