Course: 2.7 合理函数图 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 逻辑函数图

Collapse Expand
逻辑函数图
We have investigated rational functions in prior lessons, and described them loosely as functions that involve the division of .

Can the answers to a rational function be found by graphing? How would you go about graphing them?
::可以通过图形化找到理性函数的答案吗? 你会如何用图表化它们呢 ?

Graphing Rational Functions
::图形推理函数

Any function that has the form
::带有窗体的任何函数

$\begin{aligned} f (x) = \frac{P (x)}{Q (x)} \end{aligned}$

:fx)=P(x)Q(x)

where $\begin{aligned} P (x) \end{aligned}$ and $\begin{aligned} Q (x) \end{aligned}$ are polynomials and $\begin{aligned} Q (x) \neq 0 \end{aligned}$ , is called a rational function . The domain of any rational function includes all real numbers $\begin{aligned} x \end{aligned}$ that do not make the denominator zero.
::P(x) 和 Q(x) 是多元函数和 Q(x) Q(x) =0 被称作合理函数。任何合理函数的域包括所有不使分母为零的真实数字 x 。

Just like polynomials, rational functions can be graphed using transformations . The main point to remember for graphing rational functions by transformations is that some transformations change the asymptotes while others do not.
::和多面函数一样, 理性函数可以用变换来图形化。在用变换来图形化理性函数时, 需要记住的要点是, 有些变换会改变无符号, 而另一些变换则不会改变。

$\begin{aligned} r (x) + c \end{aligned}$ is a vertical shift which moves each horizontal asymptote up $\begin{aligned} c \end{aligned}$ units (or down if $\begin{aligned} c < 0 \end{aligned}$ ).
::r( x) +c 是一个垂直移动, 将每个水平的单点向上移动 c 单位( 如果 c< 0 ) , 或向下移动。

$\begin{aligned} r (x - c) \end{aligned}$ is a horizontal shift which moves each vertical asymptote right $\begin{aligned} c \end{aligned}$ units (or left if $\begin{aligned} c < 0 \end{aligned}$ ).
::r( x- c) 是一个水平移动, 移动每个垂直的单点向右 C 单位( 或如果 c< 0 则向左 ) 。

$\begin{aligned} a \cdot r (x) \end{aligned}$ is a vertical stretch which moves by a multiple of $\begin{aligned} a \end{aligned}$ (so this moves the horizontal asymptote closer to the $\begin{aligned} x - \end{aligned}$ axis if $\begin{aligned} a < 0 \end{aligned}$ .
::ar(x) 是一个垂直伸展, 以一个数的倍移动( 因此, 如果是 < 0 , 则将水平同量移动到更接近 x- 轴处 ) 。

$\begin{aligned} r (a \cdot x) \end{aligned}$ is a horizontal compression which moves the closer to $\begin{aligned} y - \end{aligned}$ axis by a factor of $\begin{aligned} \frac{1}{a} \end{aligned}$ .
::r(ax) 是水平压缩, 将接近 y- 轴移动到 1a 的系数。

$\begin{aligned} r (- x) \end{aligned}$ is a reflection about the $\begin{aligned} y - \end{aligned}$ axis. All vertical asymptotes are also reflected.
:- x) 是 Y - 轴的反射。所有垂直的微粒也均被反射。

$\begin{aligned} - r (x) \end{aligned}$ is a reflection about the $\begin{aligned} x - \end{aligned}$ axis. All horizontal asymptotes are also reflected.
::~r(x) 是 X - 轴的反射。所有水平的单位数也都被反射。

Examples
::实例

Example 1
::例1

What is the domain of $\begin{aligned} f (x) = \frac{1}{x} \end{aligned}$ ?
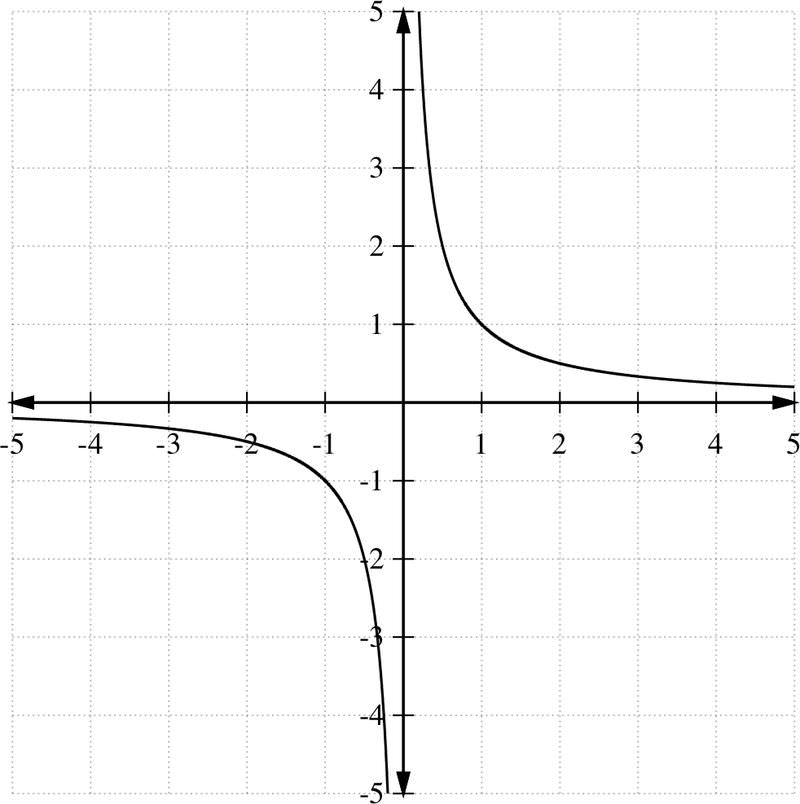
::f( x) = 1x 的域是什么 ?

Notice that the only input that can make the denominator equal to zero is $\begin{aligned} x = 0 \end{aligned}$ . Thus we say that the domain of $\begin{aligned} f (x) \end{aligned}$ is all real numbers except $\begin{aligned} x = 0 \end{aligned}$ . When looking at the graph of $\begin{aligned} f (x) = \frac{1}{x} \end{aligned}$ (see Example 2 below), you will notice that as $\begin{aligned} x \end{aligned}$ approaches 0 from the left, $\begin{aligned} f (x) \end{aligned}$ decreases. But when $\begin{aligned} x \end{aligned}$ approaches 0 from the right, $\begin{aligned} f (x) \end{aligned}$ increases. Because of this behavior, the $\begin{aligned} x - \end{aligned}$ axis and $\begin{aligned} y - \end{aligned}$ axis play the role of horizontal and vertical asymptotes , respectively.
::注意使分母等于零的唯一输入为x=0。因此, 我们说 f( x) 域是除 x=0 外的所有真实数字。当查看 f( x) = 1x 的图形( 见下文示例 2) 时, 您会注意到, 当 x 向左移动 0 时, f( x) 就会减少。但是当 x 向右移动 0 时, f( x) 就会增加。由于此行为, x- 轴和 y- 轴将分别发挥水平和垂直的同量的作用。

Example 2
::例2

Graph the function $\begin{aligned} f (x) = \frac{1}{x} \end{aligned}$ .
::函数 f( x) = 1x 的图形。

We know that the domain of $\begin{aligned} f (x) \end{aligned}$ is all real numbers excluding $\begin{aligned} x = 0 \end{aligned}$ . The vertical line $\begin{aligned} x = 0 \end{aligned}$ is called a vertical asymptote. For $\begin{aligned} x < 0, f (x) < 0, \end{aligned}$ and for $\begin{aligned} x > 0, f (x) > 0 \end{aligned}$ . Plotting a few sample points should indicate the shape of $\begin{aligned} f (x) \end{aligned}$ .
::我们知道f(x) 域是除x=0以外的所有真实数字。垂直线x=0被称为垂直静态。对于 x<0,f(x) <0, 和 x>0,f(x)>0, 和 x>0, 垂直线x=0, 垂直线x=0 被称为垂直静态。绘制几个样本点时应该显示 f(x) 的形状。

$\begin{aligned} x & 1 & 2 & 10 & \frac{1}{5} & \frac{1}{10} & - 1 & - \frac{1}{2} & - \frac{1}{10} & - 2 & - 10 \\ f (x) = \frac{1}{x} & 1 & \frac{1}{2} & \frac{1}{10} & 5 & 10 & - 1 & - 2 & - 10 & - \frac{1}{2} & - \frac{1}{10} \end{aligned}$

::x121015110-1-1-1-12-110-2-10f-10f(x)=1x1111110510-1-2-10-12-110

Example 3
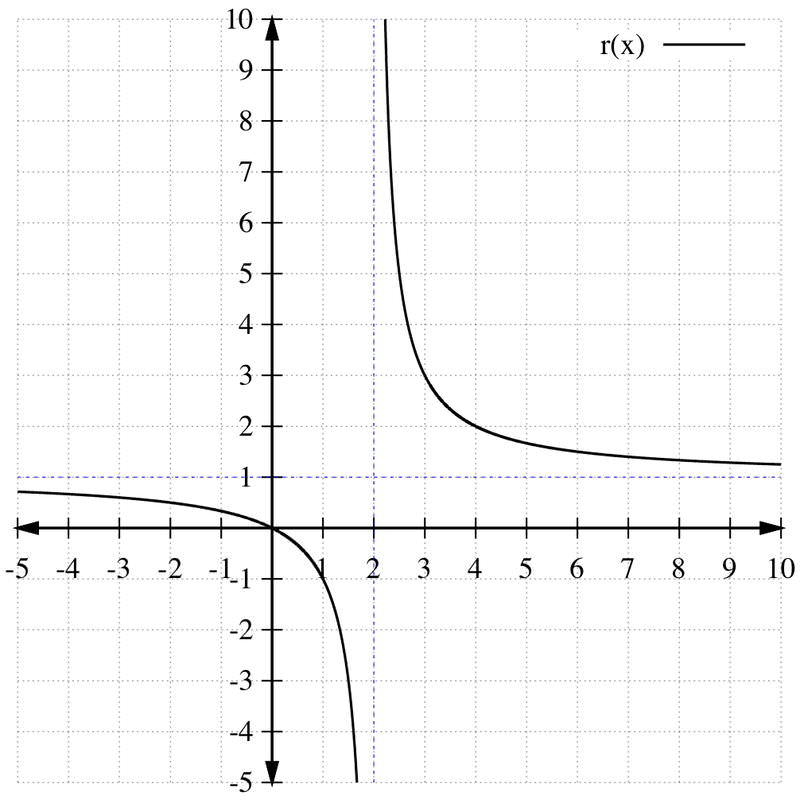
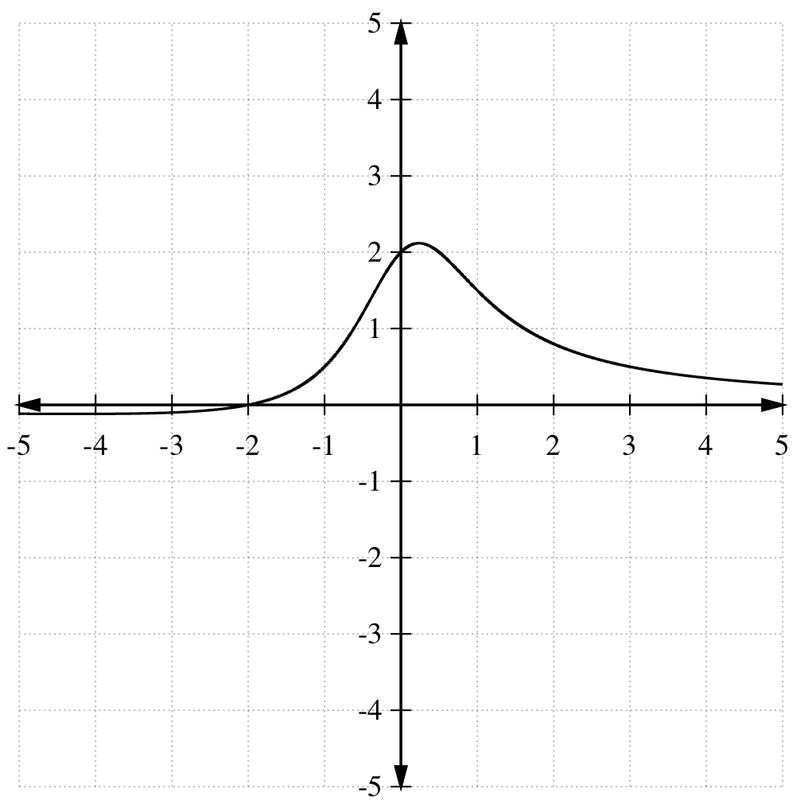
::例3

A rational function $\begin{aligned} r (x) \end{aligned}$ is shown in the figure below.
::合理函数 r(x) 如下图所示。

Use the graph of $\begin{aligned} r (x) \end{aligned}$ to sketch graphs of:
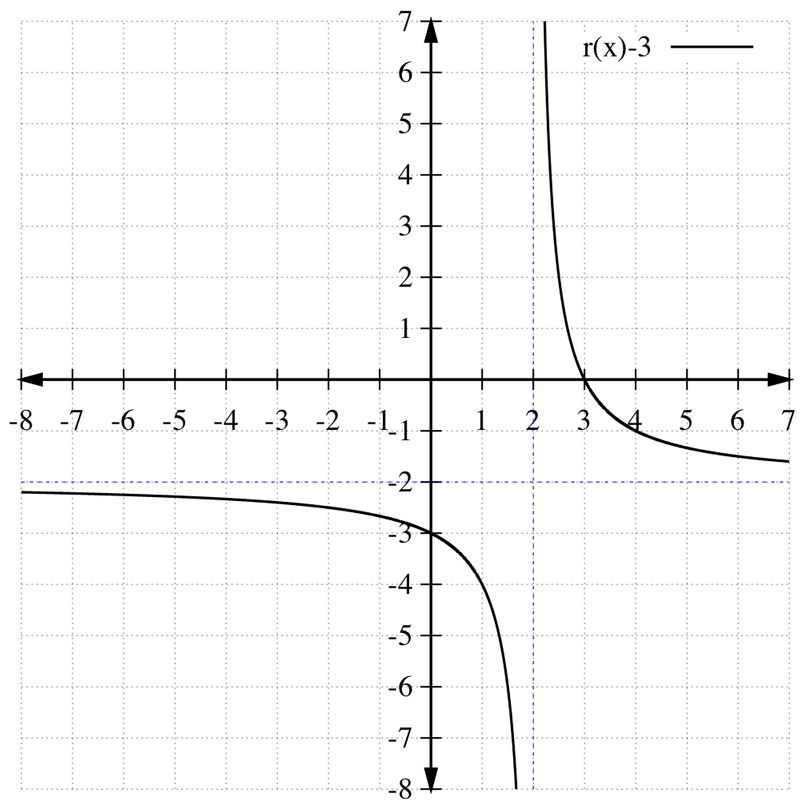
::使用 r( x) 的 r 图形来绘制 :

a. $\begin{aligned} r (x) - 3 \end{aligned}$
::a. r(x)-3

The horizontal asymptote moves down by three units.
::水平向下移动三个单位。

b. $\begin{aligned} - r (x) \end{aligned}$
::b.-r(x)

The function is reflected about the $\begin{aligned} x - \end{aligned}$ axis so the horizontal asymptote is also reflected.
::函数在 x - 轴上被反映,所以水平静态也得到反映。

c. $\begin{aligned} r (3 - x) \end{aligned}$
::c. r(3-x)

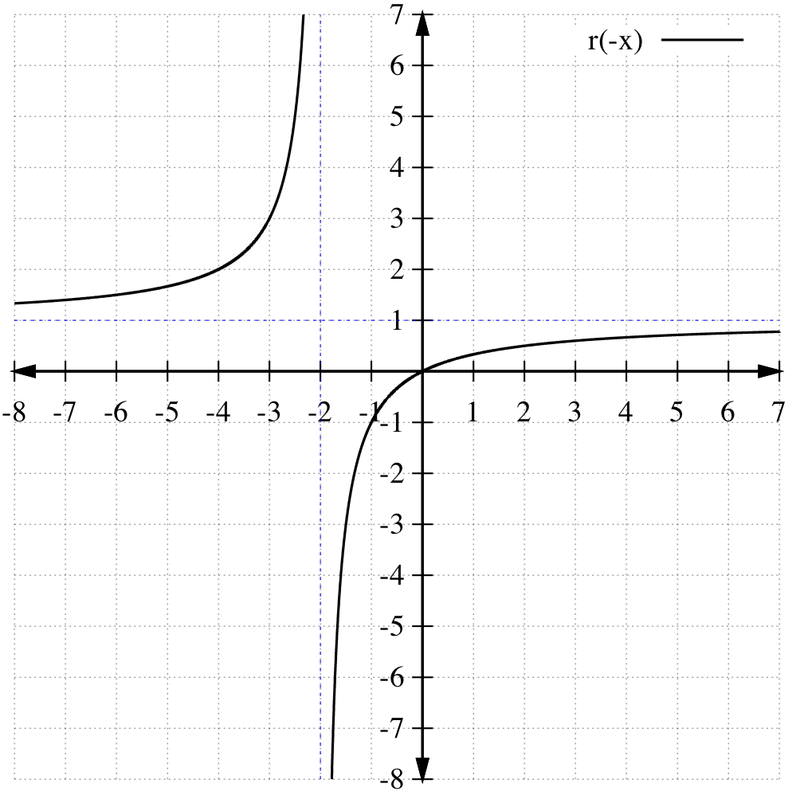
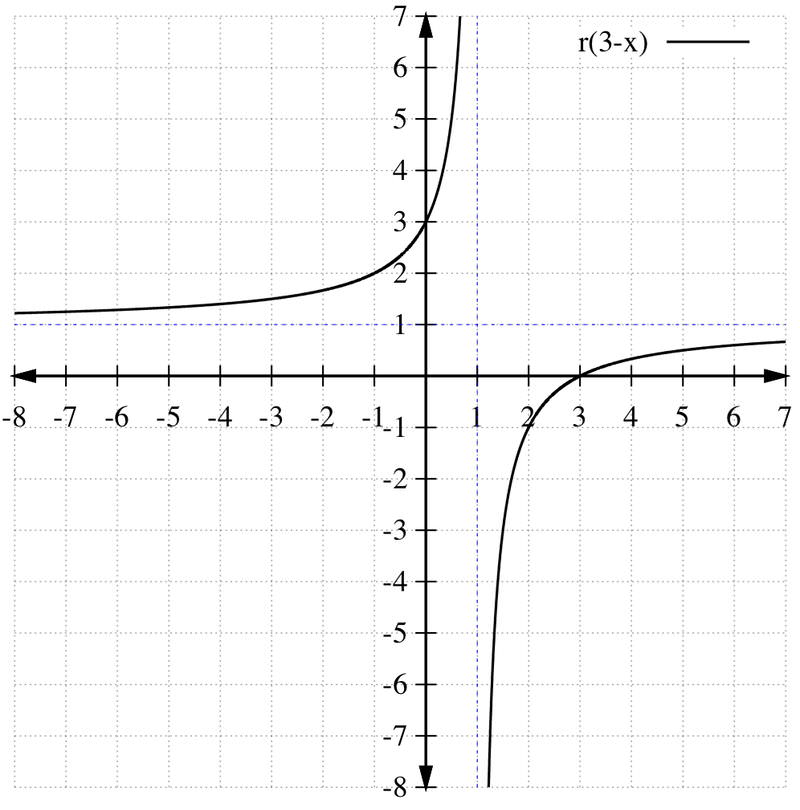
$\begin{aligned} r (3 - x) = r (- (x - 3)) \end{aligned}$ . First, graph $\begin{aligned} r (- x) \end{aligned}$ , and then shift that graph three units to the right to get $\begin{aligned} r (- (x - 3)) \end{aligned}$ . The new vertical asymptote is $\begin{aligned} x = 1 \end{aligned}$ .
::r( 3- x) =r (- (x- 3) 。首先, 图形 r (- x) , 然后将图形 3 单位移动到右侧以获得 r (- (x- 3) 。新的垂直静态为 x= 1 。

Example 4
::例4

For the following rational function, determine the domain, the asymptotes, the $\begin{aligned} x - \end{aligned}$ and $\begin{aligned} y - \end{aligned}$ intercepts and then sketch the graph.
::对于以下的理性函数,请确定域、小数、 x- 和 y- interviews,然后绘制图表。

$\begin{aligned} f (x) = \frac{x + 2}{x^{2} + 1} \end{aligned}$
:xx) =x+2x2+1

To identify domain limitations, find value(s) which make the denominator = 0: In this case, where $\begin{aligned} x^{2} \end{aligned}$ , the only variable in the denominator, is added to 0 , any value for x will be positive. So the domain is all real numbers.
::为了确定域限, 找到使分母= 0的值 : 在这种情况下, x2 分母中唯一的变量被添加到 0, x 的任何值都将是正值。因此, 域是所有真实数字。

With no limitations on the domain, there are no vertical asymptotes.
::在对域没有限制的情况下,不存在垂直的零星状态。

The horizontal asymptote: $\begin{aligned} y = 0 \end{aligned}$ becomes apparent as x becomes huge and the "+2" and "+1" no longer have an effect, giving: $\begin{aligned} f (x) = \frac{x}{x^{2}} \to f (x) = \frac{1}{x} \to f (x) = 0 \end{aligned}$ So the horizontal asymptote is 0
::水平线状数 : y=0 当 x 变大, "+2" 和 "+1" 不再具有效果时, y=0 变得明显, 也就是说: f( x) =xx2\f( x) =1xx}f( x) =1x*f( x) =0 水平线状数为 0

Example 5
::例5

For the following rational function, determine the domain, the asymptotes, the $\begin{aligned} x - \end{aligned}$ and $\begin{aligned} y - \end{aligned}$ intercepts and then sketch the graph.
::对于以下的理性函数,确定域、小数、轴-和-截取,然后绘制图表。

$\begin{aligned} f (x) = \frac{9 x^{2} - 4}{3 x + 2} \end{aligned}$
:xx)=9x2 - 43x+2

For this problem, the first step is to recognize the difference of squares in the numerator: $\begin{aligned} 9 x^{2} - 4 \end{aligned}$ which factors easily into $\begin{aligned} (3 x - 2) (3 x + 2) \end{aligned}$
::对于这一问题,第一步是承认分子中的方形差异:9x2-4,其因素很容易进入(3x-2)(3x+2)

This gives: $\begin{aligned} f (x) = \frac{(3 x - 2) (3 x + 2)}{(3 x + 2)} \end{aligned}$
::这给出了 : f( x) = (3x-2) (3x+2) (3x+2) (3x+2) 。

NOTE: Although we can cancel the (3x + 2) to evaluate the general behavior of the function, giving: $\begin{aligned} f (x) = 3 x + 2 \end{aligned}$ (which is just a line), that does not change the fact that a zero in the denominator of the equation is undefined , it just means that the rest of the function behaves like $\begin{aligned} y = 3 x - 2 \end{aligned}$ .
::注:虽然我们可以取消用于评价函数一般行为的3x+2, 给出: f( x)=3x+2( 这只是一行), 这并不改变方程式分母中零的未定义这一事实, 但它只是意味着函数的其余部分行为像 y=3x-2 。

To identify domain limitations, find value(s) which make the denominator = 0: In this case: $\begin{aligned} 3 x + 2 = 0 \to 3 x = - 2 \to x = - \frac{2}{3} \end{aligned}$ which means the domain cannot include a value of -2/3 for x : $\begin{aligned} x \neq - \frac{2}{3} \end{aligned}$
::为了确定域限, 找到使分母= 0 的值 : 在此情况下 : 3x+2= 0}3x2x= 03x 2xx 23 表示域不能包含 x: x\ 23 的 - 2/3 值。

Since the equation behaves as a line with a single non-existent value, there is no vertical asymptote.
::由于方程式行为是一行单一无值的直线,因此不存在垂直零星现象。

As x gets huge, we end up with $\begin{aligned} f (x) = \frac{9 x^{2}}{3 x} \to f (x) = 3 x \end{aligned}$ which is a slant asymptote that parallels the line of the function!
::当 x 变大时, 我们的结局是 f( x) = 9x23xx}f( x) = 3x, 这是一种与函数线平行的倾斜无状物 !

Review
::回顾

What is the hole in the graph of a function called?
::函数图形中的空洞叫什么?

How are polynomial graphs different from rational function graphs?
::多元图形与理性函数图形有何不同?

What does the graph of the simplified function that is continuous everywhere not have?
::无处不在的连续的简化函数图是什么?

Why can't rational function be simplified to determine the domain?
::为什么不能简化理性功能来确定域名?

Put the following steps into the correct order for graphing rational functions. a) Find all asymptotes. b) Sketch a smooth graph based on the information. c) Factor numerator and denominator completely and put in lowest terms. Identify any holes. d) Determine the behavior around the vertical asymptotes using a table of signs. e) Find all intercepts. f) Find the places where the function crosses the horizontal asymptote/oblique asymptote.
::将以下步骤置于绘制理性函数图表的正确顺序中。 a) 查找所有无线点。 b) 根据信息绘制一个平滑的图表。 c) 参数数和分母完全完整,并以最低值表示。识别任何洞。 d) 使用符号表确定垂直静点周围的行为。 e) 查找所有拦截。 f) 查找函数横线线线线数/单线点的交叉点。

Simplify $\begin{aligned} \frac{6 x^{2} + 21 x + 9}{4 x^{2} - 1} \end{aligned}$
::简化 6x2+21x+94x2- 1

Given: $\begin{aligned} y = \frac{x^{2} + 2 x - 8}{x} \end{aligned}$ . Find the intercepts, any asymptotes, and identify end behavior.
::给定值 : y=x2+2x-8x。查找拦截、任何微量, 并识别最终行为。

Graph the equation and state the domain.
::绘制方程图并标出域。

Simplify each function in questions 9 and 10 and state any value(s) of x that make the function undefined.
::简化问题9和问题10中的每一项功能,并说明使函数未定义的 x 的任何值。

$\begin{aligned} f (x) = \frac{3 - x}{x^{2} - 3 x} \end{aligned}$
:xx)=3-x22-3x

$\begin{aligned} f (x) = \frac{x^{2} - 2 x - 15}{x - 5} \end{aligned}$
:xx) =x2-2x-15x-5

For each function in questions 11-13, identify points of discontinuity and the form of the graph of the simplified function (linear or quadratic).
::对于问题11-13中的每个函数,指明不连续点和简化函数(线性或二次函数)图的形式。

$\begin{aligned} f (x) = \frac{2 x^{2} + x - 1}{2 x - 1} \end{aligned}$
:xx) = 2x2+x- 12x- 1

$\begin{aligned} f (x) = \frac{- 2 x^{3} + 9 x^{2} - 10 x + 3}{x - 3} \end{aligned}$
:xx) 2x3+9x2-10x+3x-3

$\begin{aligned} f (x) = \frac{x^{3} - 13 x - 12}{x^{2} - 3 x - 4} \end{aligned}$
:x) =x3-13x-12x2-3x-4

Write a quadratic function where the domain cannot include 5 or -5, and the graph has two asymptotes
::写入一个二次函数, 域域不能包括 5 或 5 或 5 , 而图形有两个小数

Simplify, identify the asymptotes and intercepts, and sketch the graph of $\begin{aligned} f (x) = \frac{x^{3} - 64 x}{x^{2} - 16} \end{aligned}$
::简化、识别小行星和拦截物,绘制f(x)=x3-64x2-16的图表图

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

逻辑函数图

Graphing Rational Functions ::图形推理函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Review ::回顾

Review (Answers) ::回顾(答复)

Graphing Rational Functions
::图形推理函数

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Review
::回顾

Review (Answers)
::回顾(答复)