Course: 2.9 赤道不平等 | The Way To Learn

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

赤道不平等

How would you express the following as a function ?
::你如何作为职能表达以下内容?

You are supposed to mow your square-shaped lawn for your parents, but the mower only has part of a tank of gas. If you can mow 2500 sf per gallon, and the mower has approximately 2.5 gallons in it, what is the maximum length of one side of the lawn you can mow? If your lawn is 75 feet long, will you need more gas?
::你应该为父母修剪草坪,但割草机只有油箱的一部分。如果你能每加仑修剪2500索夫,而除草机里有大约2.5加仑,那么,可以修剪的草坪的最长长度是多少?如果你的草坪长75英尺,你还需要更多的油吗?

Quadratic Inequalities
::赤道不平等

Quadratic inequalities are inequalities that have one of the following forms
::严重不平等是具有以下形式之一的不平等:

\begin{aligned} a x^{2} + b x + c > 0 \end{aligned}

::ax2+bx+c>0

and
::和

\begin{aligned} a x^{2} + b x + c < 0 \end{aligned}

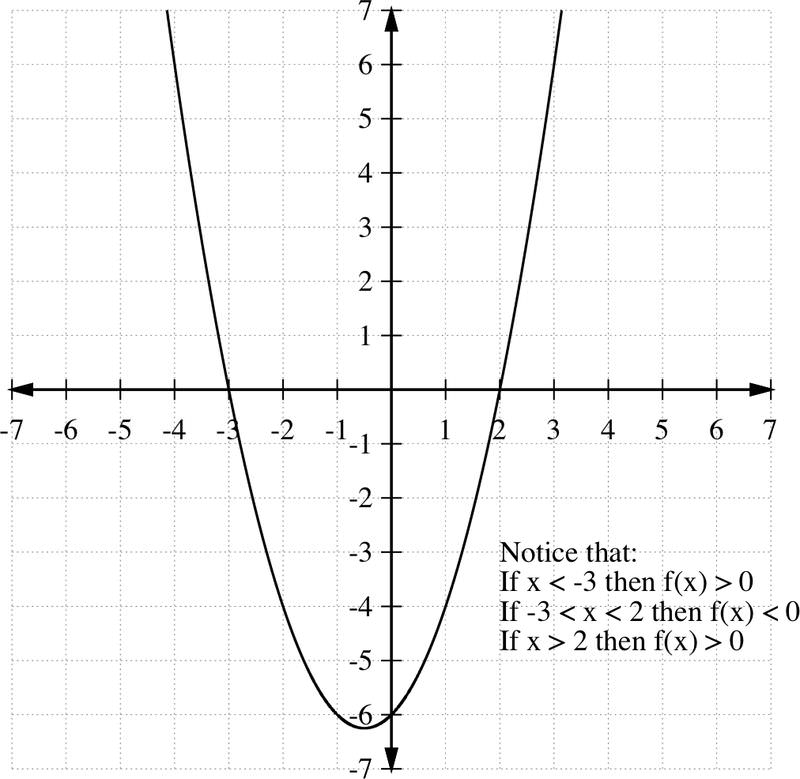
::ax2+bx+c <0

We can solve these inequalities by using the techniques that we have learned about solving quadratic equations. For example, consider the graph of the equation :
::我们可以利用我们所学的解决二次方程式的技术来解决这些不平等问题。例如,考虑方程式的图表:

\begin{aligned} y = f (x) = x^{2} + x - 6 \end{aligned}

::y=f(x)=x2+x-6

Notice that the curve intersects the $\begin{aligned} x - \end{aligned}$ axis at -3 and 2. From graph, we notice the followings
::注意曲线交叉 x - 轴值为 - 3 和 2 。我们从图表中注意到以下

If $\begin{aligned} x < - 3 \end{aligned}$ then $\begin{aligned} f (x) > 0 \end{aligned}$
::如果 x3 然后 f( x) >0

If $\begin{aligned} - 3 < x < 2 \end{aligned}$ , then $\begin{aligned} f (x) < 0 \end{aligned}$
::如果 - 3 <x <2, 那么f(x) <0

If $\begin{aligned} x > 2 \end{aligned}$ , then $\begin{aligned} f (x) > 0 \end{aligned}$
::如果 x> 2, 然后 f( x) > 0

Therefore , $\begin{aligned} x^{2} + x - 6 > 0 \end{aligned}$ whenever $\begin{aligned} x < - 3 \end{aligned}$ or $\begin{aligned} x > 2 \end{aligned}$ , and $\begin{aligned} x^{2} + x - 6 < 0 \end{aligned}$ when $\begin{aligned} - 3 < x < 2 \end{aligned}$ .
::因此,在 x2+x-6>0 和 x2+6 <0 和 3 <x < 2 时,均值为 x2+x-6>0。

Examples
::实例

Example 1
::例1

Earlier, you were given a question about mowing a lawn.
::之前有人问过你割草草的事

If you can mow 2500 sf of grass per gallon of gas, and the mower has 2.5 gallons in it, what is the maximum length of one side of the lawn you can mow?
::如果你每加仑的气体能修剪2500平方米的草, 而除草机里有2.5加仑的草, 草坪一边的最长长度是多少?

If your lawn is 75 ft long, will you need more gas?
::如果你的草坪长75英尺,你还需要汽油吗?

We know that the function $\begin{aligned} S^{2} < 6250 \end{aligned}$ describes the possible side lengths of square shapes you could mow before running out of gas (if you're having trouble understanding why, see Example 4 for a similar process).
::我们知道 S2 < 6250 函数描述了在用完天然气之前您可以修剪的方形的侧边长度( 如果您不明白原因, 类似过程请参见例4)。

Solving for S gives:
::S 给定的解析 :

\begin{aligned} \sqrt{s^{2}} = \sqrt{6250} \end{aligned}

\begin{aligned} s = 79 \end{aligned}

With 2.5 gal of gas, you could mow a square up to apx 79 ft on each side.
::有了2.5个煤气女, 你可以把方块切成每边的Apx 79英尺

You should not need more gas if the lawn is only 75 ft long on each side.
::如果草坪每侧只有75英尺长,就不需要更多气体了。

Example 2
::例2

What is the solution set of the inequality $\begin{aligned} 2 x^{2} + 7 x - 4 < 0 \end{aligned}$ ?
::不平等2x2+7x-4<0的解决方案是什么?

It is best to graph the function $\begin{aligned} f (x) = 2 x^{2} + 7 x - 4 \end{aligned}$ and look for the values of $\begin{aligned} x \end{aligned}$ such that the inequality $\begin{aligned} f (x) < 0 \end{aligned}$ is true.
::最好将函数 f( x) = 2x2+7x-4 图形化, 并查找 x 的值, 这样不平等 f( x) < 0 是真实的。

Thus from graph, $\begin{aligned} 2 x^{2} + 7 x - 4 < 0 \end{aligned}$ only if
::从图形2x2+7x-4<0

\begin{aligned} - 4 < x < \frac{1}{2} \end{aligned}

::− 4 < x < 12

So the solution set is $\begin{aligned} x \in (- 4, \frac{1}{2}) \end{aligned}$ or in set builder notation, $\begin{aligned} {x | - 4 < x < \frac{1}{2}} \end{aligned}$
::所以解决方案集是 x(- 4, 4, 12) 或设置构建符符号 {x4 < x < 12} 。

Although the method of graphing to find the solution set of an inequality is easy to follow, another algebraic method can be used. The algebraic method involves finding the $\begin{aligned} x - \end{aligned}$ intercepts of the graph and then dividing the $\begin{aligned} x - \end{aligned}$ axis into intervals separated by the $\begin{aligned} x - \end{aligned}$ intercepts. The examples below illustrate the method.
::虽然找到不平等的一套解决办法的图表方法很容易遵循,但也可以使用另一种代数法。代数法包括找到图形的x-截取点,然后将x-轴分割成由x-截取点分开的间隔。下面的例子说明了该方法。

Example 3
::例3

Find the solution set of the quadratic inequality $\begin{aligned} x^{2} + 2 x - 8 > 0 \end{aligned}$ without graphing.
::找到二次不平等 x2+2x-8>0 的解决方案集, 不绘制图形。

To find the solution set without graphing, first factor :
::要找到没有图形化的解决方案集,第一个因素是:

$\begin{aligned} x^{2} + 2 x - 8 = 0 \end{aligned}$
::x2+2x-8=0

$\begin{aligned} (x + 4) (x - 2) = 0 \end{aligned}$
:x+4)(x-2)=0

Recalling the zero product rule , we can see that the two solutions to this quadratic equation are $\begin{aligned} x = - 4 \end{aligned}$ and $\begin{aligned} x = 2 \end{aligned}$ , thus, the $\begin{aligned} x - \end{aligned}$ intercepts of the function $\begin{aligned} f (x) = x^{2} + 2 x - 8 \end{aligned}$ are -4 and 2.
::回顾零产品规则,我们可以看到,这一二次方程式的两个解决办法是x4和x=2,因此,函数f(x)=x2+2x-8的X-interphies是-4和2。

These points divide the $\begin{aligned} x - \end{aligned}$ axis into three intervals: $\begin{aligned} (- \infty, - 4) | (- 4, 2) | (2, \infty) \end{aligned}$ . We can choose a test point from each interval, substitute it into $\begin{aligned} f (x) \end{aligned}$ and see if the function is negative or positive with that value as x . This procedure can be simplified by making a table as shown below:
::这些点将 x- 轴分为三个间隔,- 4) (- 4) (- 4, 2) ( 2, ) 。我们可以从每个间隔选择一个测试点, 将其替换为 f( x) , 并查看该函数是否为负值或正值, 如 x。可以通过下表简化此程序 :

Interval	Test Point	Is $\begin{aligned} x^{2} + 2 x - 8 \end{aligned}$ positive or negative?	Part of Solution set?
$\begin{aligned} (- \infty, - 4) \end{aligned}$	$\begin{aligned} - 5 \end{aligned}$	$\begin{aligned} + \end{aligned}$	$\begin{aligned} y e s \end{aligned}$
$\begin{aligned} (- 4, 2) \end{aligned}$	$\begin{aligned} 1 \end{aligned}$	$\begin{aligned} - \end{aligned}$	$\begin{aligned} n o \end{aligned}$
$\begin{aligned} (2, + \infty) \end{aligned}$	$\begin{aligned} 3 \end{aligned}$	$\begin{aligned} + \end{aligned}$	$\begin{aligned} y e s \end{aligned}$

From the table, we conclude that since $\begin{aligned} x^{2} + 2 x - 8 > 0 \end{aligned}$ if and only if $\begin{aligned} x < - 4 \end{aligned}$ and $\begin{aligned} x > 2 \end{aligned}$ . The solution set can also be written as:
::我们从表中得出结论,自 x2+2x-8>0 以来,如果且只有在 x4 和 x>2 的情况下,才会使用以下方式来写出所设定的解决方案:

\begin{aligned} x \in (- \infty, - 4) \cup (2, + \infty) \end{aligned}

Some problems in science involve quadratic inequalities. The example below illustrates one such application.
::科学方面的一些问题涉及二次不平等,下面的例子说明了这种应用。

Example 4
::例4

A rectangle has a length 10 meters more than twice the width. Find all of the possible widths that result in the area of the rectangle not exceeding 100 squared meters.
::矩形的长度是宽度的两倍。查找所有可能导致矩形区域不超过100平方米的宽度。

Let $\begin{aligned} w \end{aligned}$ be the width of the rectangle and $\begin{aligned} l \end{aligned}$ its length. Given the information in the question, we can say:
::让我们成为矩形宽度和长度。根据问题的信息,我们可以说:

$\begin{aligned} l = 10 + 2 w \end{aligned}$
::l=10+2w

Then we can use the formula for the area of a rectangle:
::然后我们可以用公式来表示矩形区域:

$\begin{aligned} a r e a = l \times w \end{aligned}$
::区域=lxw

Substituting $\begin{aligned} 10 + 2 w \end{aligned}$ in for $\begin{aligned} l \end{aligned}$ gives:
::替代 10+2w 的 I 给付 :

$\begin{aligned} a r e a = w \times (10 + 2 w) \end{aligned}$
::区域=wxx(10+2w)

$\begin{aligned} = 2 w^{2} + 10 w \end{aligned}$
::=2w2+10w

The area cannot exceed $\begin{aligned} 100 m^{2} \end{aligned}$ , so
::该面积不得超过100平方米,所以

\begin{aligned} 10 w + 2 w^{2} < 100 \end{aligned}

::10w+2w2 < 100

or
::或

\begin{aligned} 2 w^{2} + 10 w - 100 < 0 \end{aligned}

::2w2+10w-100 <0

Simplify by dividing both sides by 2:
::将双方除以2:

\begin{aligned} w^{2} + 5 w - 50 < 0 \end{aligned}

::W2+5w-50 <0

Factor the trinomial :
::三进制因数 :

\begin{aligned} w^{2} + 5 w - 50 = (w + 10) (w - 5) \end{aligned}

::w2+5w- 50=(w+10)(w-5)

So the partition points are 5 and -10, which means we have three intervals. Since width cannot be negative, we can safely ignore -10. That means the maximum area is $\begin{aligned} 100 m^{2} \end{aligned}$
::分区点为 5 和 - 10 , 这意味着我们有三个间隔。由于宽度不能为负负, 我们可以安全忽略 - 10。这意味着最大面积为 100 平方米

$\begin{aligned} ∴ w < 5 \end{aligned}$ .
::Ww <5。。。

The width must be less than 5 meters.
::宽度必须小于5米。

Example 5
::例5

Find the solution set of the inequality $\begin{aligned} x^{2} \leq 16 \end{aligned}$ .
::寻找不平等的解决方案集 x216 。

Set the function equal to zero:
::设定函数为 0:

$\begin{aligned} x^{2} - 16 = 0 \end{aligned}$
::x2 - 16=0

Factor to find the critical values (points where the graph crosses the x axis, thereby changing signs):
::查找关键值的系数( 图形通过 x 轴的点, 从而改变符号 ) :

$\begin{aligned} (x - 4) (x + 4) = 0 \end{aligned}$
:x-4)(x+4)=0

By the zero product rule: $\begin{aligned} x = 4 \end{aligned}$ or $\begin{aligned} x = - 4 \end{aligned}$
::根据零产品规则: x=4 或 x4

That gives us three sections on the graph:
::这让我们在图表上分为三个部分:

$\begin{aligned} x \leq - 4 \end{aligned}$
::x4

$\begin{aligned} - 4 \leq x \leq 4 \end{aligned}$
::- 4x4 - 4x4

$\begin{aligned} 4 \leq x \end{aligned}$
::4x

Test one sample value from each division to identify possible solution sets.
::测试每个分部的一个样本值,以确定可能的解决方案组。

Set	$\begin{aligned} x \leq - 4 \end{aligned}$	$\begin{aligned} - 4 \leq x \leq 4 \end{aligned}$	$\begin{aligned} 4 \leq x \end{aligned}$
Test value	$\begin{aligned} - 5 \end{aligned}$		$\begin{aligned} 5 \end{aligned}$
$\begin{aligned} f (x) \end{aligned}$ true with value?	$\begin{aligned} 4 \cdot (- 5)^{2} = 100 ≰ 16 \end{aligned}$ $\begin{aligned} ∴ N o \end{aligned}$	$\begin{aligned} 4 \cdot 0^{2} = 0 \leq 16 \end{aligned}$ $\begin{aligned} ∴ Y e s \end{aligned}$	$\begin{aligned} 4 \cdot 5^{2} = 100 ≰ 16 \end{aligned}$ $\begin{aligned} ∴ N o \end{aligned}$

Therefore the solution set is $\begin{aligned} - 4 \leq x \leq 4 \end{aligned}$ .
::因此,解决办法是-4x4。

Example 6
::例6

Graph the solution set: $\begin{aligned} (x - 3) (x + 4) \geq 0 \end{aligned}$ .
::溶液集图x-3)(x+4)%0 。

The solutions to $\begin{aligned} (x - 3) (x + 4) \geq 0 \end{aligned}$ can be identified with the rules for multiplying negative numbers:
:x-3)(x+4)%0的解决方案与负数乘法规则相同:

Recall from Pre-Algebra that an even number of negatives yields a positive answer, and an odd number of negatives yields a negative answer.
::上市前回顾,即使是负数也得出了正回答,奇数的负数也得出了负回答。

Since $\begin{aligned} (x - 3) (x + 4) \geq 0 \end{aligned}$ we know we need a positive answer or zero.
::由于(x-3)(x+4)0,我们知道我们需要正面回答或零回答。

Therefore either:
::因此:

Case #1: $\begin{aligned} (x - 3) \geq 0 \to x \geq 3 \end{aligned}$ and $\begin{aligned} (x + 4) \geq 0 \to x \geq - 4 \end{aligned}$
::案例 # 1 (x- 3) : (x- 3) 0x% 3 和 (x+4) 0x% 4

or
::或

Case #2: $\begin{aligned} (x - 3) \leq 0 \to x \leq 3 \end{aligned}$ and $\begin{aligned} (x + 4) \leq 0 \to x \leq - 4 \end{aligned}$
::案例2: (x- 3) : (x- 3) 0x 3 和(x+4) +0x 4

Since any number greater than 3 is already greater than -4, from Case #1 we get: $\begin{aligned} x \geq 3 \end{aligned}$
::因为任何超过3号的数已经超过4号从1号案例中,我们得到的是:x%3

Since any number less than -4 is already less than 3, from Case #2 we get $\begin{aligned} x \leq - 4 \end{aligned}$
::因为任何小于 - 4 的数已经小于 3, 从案件# 2, 我们得到 x @ @ 4

Therefore our answer is $\begin{aligned} x \leq - 4 \end{aligned}$ or $\begin{aligned} x \geq 3 \end{aligned}$
::因此,我们的回答是 x4orx3

In set notation : $\begin{aligned} x \in (- \infty, - 4] \cup [3, + \infty) \end{aligned}$
::设定符号: x(),-/4}[3,]

To graph this information, we draw a line graph, and mark the values that x can be , with solid dots on the end numbers to indicate that those values are included.
::要绘制此信息图, 我们绘制一个线条图, 并标记 x can 的值, 在终点点上加上实点, 以显示这些值包含在内。

Visually that is:
::从视觉上看,这就是:

Review
::回顾

Graph the solutions sets below on a number line:
::下面用数字行绘制的解决方案图:

$\begin{aligned} x < 3 \end{aligned}$ or $\begin{aligned} x > 4 \end{aligned}$
::x3orx>4

$\begin{aligned} x \geq - 5 \end{aligned}$ and $\begin{aligned} x \geq 3 \end{aligned}$
::x5 和x% 3

$\begin{aligned} x < 6 \end{aligned}$ and $\begin{aligned} x \geq - 2 \end{aligned}$
::x6 和x%% 2

$\begin{aligned} x > 7 \end{aligned}$ or $\begin{aligned} x \geq - 4 \end{aligned}$
::x>7orx4

$\begin{aligned} x < - 8 \end{aligned}$ and $\begin{aligned} x > 3 \end{aligned}$
::x8andx > 3

Identify critical points, solve, and graph:
::确定临界点、解决点和图表:

$\begin{aligned} x^{2} + 9 x > - 14 \end{aligned}$
::x2+9x14

$\begin{aligned} x^{2} - 5 x \leq 50 \end{aligned}$
::x2 - 5x=50

$\begin{aligned} x^{2} + 2 x \leq 48 \end{aligned}$
::x2+2x48

$\begin{aligned} x - \frac{20}{x} - 8 < 0 \end{aligned}$ (hint: multiply both sides by x first)
::x-20x- 8 <0( 符号: 将两边乘以 x 1)

$\begin{aligned} x + 10 \geq - \frac{21}{x} \end{aligned}$
::x+1021x

$\begin{aligned} (x + 6) (x - 3) > 0 \end{aligned}$
:x+6)(x-3) >0

$\begin{aligned} (x - 8) (x + 1) > 0 \end{aligned}$
:x-8)(x+1) >0

$\begin{aligned} x^{2} - x > 90 \end{aligned}$
::x2 - x > 90

$\begin{aligned} 3 x^{2} - 23 x \leq 8 \end{aligned}$
::3x2 - 23x8

$\begin{aligned} x^{2} + x - 6 > 0 \end{aligned}$
::x2+x-6>0

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

赤道不平等

Quadratic Inequalities ::赤道不平等

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)