9.4 标准表格中的逻辑函数图

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 在标准表格中绘制逻辑函数

  Collapse Expand

  在标准表格中绘制逻辑函数

  播放段落

  The standard form of a rational function is given by the equation $\begin{array}{r}f(x)=\frac{a}{x-h}+k\end{array}$ . What are the asymptotes of this equation?
  ::方程式 f( x) = ax-h+k 给出了理性函数的标准格式。 此方程式的微量数是什么 ?

  播放段落

  Rational Function
  ::理性函数

  播放段落

  A rational function is in the form $\begin{array}{r}\frac{p\left(x\right)}{q\left(x\right)}\end{array}$ where $\begin{array}{r}p(x)\end{array}$ and $\begin{array}{r}q(x)\end{array}$ are and $\begin{array}{r}q(x)\ne 0\end{array}$ . The parent graph for rational functions is $\begin{array}{r}y=\frac{1}{x}\end{array}$ , and the shape is called a hyperbola .
  ::合理函数在 p( x) q( x) 和 q( x) 的窗体 p( x) 和 q( x) 和 q( x)\\ @ 。 合理函数的母图为 y= 1x, 形状被称为双曲线 。

  $\begin{array}{r}x\end{array}$	$\begin{array}{r}y\end{array}$
  $\begin{array}{r}-4\end{array}$	$\begin{array}{r}-\frac{1}{4}\end{array}$
  $\begin{array}{r}-2\end{array}$	$\begin{array}{r}-\frac{1}{2}\end{array}$
  $\begin{array}{r}-1\end{array}$	$\begin{array}{r}-1\end{array}$
  $\begin{array}{r}-\frac{1}{2}\end{array}$	$\begin{array}{r}-2\end{array}$
  $\begin{array}{r}\frac{1}{2}\end{array}$	2
  1	1
  2	$\begin{array}{r}\frac{1}{2}\end{array}$
  4	$\begin{array}{r}\frac{1}{4}\end{array}$

  

  播放段落

  Notice the following properties of this hyperbola: the $\begin{array}{r}x\end{array}$ -axis is a horizontal asymptote , the $\begin{array}{r}y\end{array}$ -axis is a vertical asymptote , and the domain and range are all real numbers except where the asymptotes are. Recall that the vertical asymptote is the value that makes the denominator zero because we cannot divide by zero. For the horizontal asymptote, it is the value where the range is not defined.
  ::注意此双曲线的以下属性: x 轴是一个水平的单点, Y 轴是一个垂直的单点, 域和范围是所有真实数字, 但小行星除外 。 请注意, 垂直的单点是导致分母零的值, 因为我们无法除以零。 对于水平的单点, 它就是没有定义范围值的值 。

  播放段落

  The two parts of the graph are called branches . In the case with a hyperbola, the branches are always symmetrical about the point where the asymptotes intersect. In this example, they are symmetrical about the origin.
  ::图形的两部分被称为分支。 在超高波拉的情况下, 树枝总是对称的, 与小粒子交叉点的点相对。 在此示例中, 它们对称于来源 。

  播放段落

  In this lesson, all the rational functions will have the form $\begin{array}{r}f(x)=\frac{a}{x-h}+k\end{array}$ .
  ::在此课程中, 所有理性函数都将包含 f( x) = ax-h+k 的表单 。

  播放段落

  Let's graph $\begin{array}{r}f(x)=\frac{-2}{x}\end{array}$  and find any asymptotes, the domain, range, and any zeros .
  ::让我们用图f(x)%%2x来查找任何小数点、域、范围以及任何零。

  播放段落

  Let’s make a table of values.
  ::让我们绘制一个数值表。

  $\begin{array}{r}x\end{array}$	$\begin{array}{r}y\end{array}$
  1	$\begin{array}{r}-2\end{array}$
  2	$\begin{array}{r}-1\end{array}$
  4	$\begin{array}{r}-\frac{1}{2}\end{array}$

  播放段落

  Notice that these branches are in the second and fourth quadrants . This is because of the negative sign in front of the 2, or $\begin{array}{r}a\end{array}$ . The horizontal and vertical asymptotes are still the $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ -axes. There are no zeros, or $\begin{array}{r}x\end{array}$ - intercepts , because the $\begin{array}{r}x\end{array}$ -axis is an asymptote. The domain and range are all non-zero real numbers (all real numbers except zero).
  ::请注意, 这些分支位于第二和第三 四分之一。 这是因为 2 或 a 前的负号。 水平和垂直的负号仍然是 x 和 y 轴。 没有零 或 x 截取, 因为 x 轴是一个小数。 域和范围都是非 零 实际数字( 除零 外的所有实际数字 ) 。

  

  播放段落

  Now, let's graph $\begin{array}{r}y=\frac{1}{x-5}+2\end{array}$  and find all asymptotes, zeros, the domain and range.
  ::现在,让我们来图y=1x-5+2, 并找到所有无症状、 零、 域和范围 。

  播放段落

  For $\begin{array}{r}y=\frac{1}{x-5}+2\end{array}$ , the vertical asymptote is $\begin{array}{r}x=5\end{array}$ because that would make the denominator zero and we cannot divide by zero. When $\begin{array}{r}x=5\end{array}$ , the value of the function would be $\begin{array}{r}y=\frac{1}{0}+2\end{array}$ , making the range undefined at $\begin{array}{r}y=2\end{array}$ . The shape and location of the branches are the same as the parent graph, just shifted to the right 5 units and up 2 units.
  ::对于 y= 1x-5+2, 垂直静态为 x=5 , 因为这将使分母为零, 我们无法除以零。 当 x=5 时, 函数的值为 y= 10+2, 使范围在 y=2 时未定义。 分支的形状和位置与 父图相同, 仅移到右 5 个单位和 上两个单位。

  

  播放段落

  Therefore , for the general form of a rational function, $\begin{array}{r}y=\frac{a}{x-h}+k,x=h\end{array}$ is the vertical asymptote and $\begin{array}{r}y=k\end{array}$ is the horizontal asymptote.
  ::因此,对于一般的理性函数形式,y=ax-h+k,x=h是垂直的静态,y=k是水平的静态。

  播放段落

  The domain is all real numbers; $\begin{array}{r}x\ne 5\end{array}$ and the range is all real numbers; $\begin{array}{r}y\ne 2\end{array}$ . To find the zero, set the function equal to zero and solve for $\begin{array}{r}x\end{array}$ .
  ::域名是所有真实数字; x5, 范围是所有真实数字; y2。 要找到零, 将函数设为零, 并解决 x 的函数 。

  播放段落

  $$\begin{array}{rl}0& =\frac{1}{x-5}+2\\ -2& =\frac{1}{x-5}\\ -2x+10& =1\\ -2x& =-9\\ x& =\frac{9}{2}=4.5\end{array}$$

  
  ::0=1x-5-5+2-2=1x-5-2x+10=1-2x9x=92=4.5

  播放段落

  To find the $\begin{array}{r}y\end{array}$ - intercept , set $\begin{array}{r}x=0\end{array}$ , and solve for $\begin{array}{r}y\end{array}$ . $\begin{array}{r}y=\frac{1}{0-5}+2=-\frac{1}{5}+2=1\frac{4}{5}\end{array}$ .
  ::要找到y- 界面, 设置 x=0, 并解决y. y= 10 - 5+2+2+15+2=145 。

  播放段落

  Finally, let's find the equation of the hyperbola below.
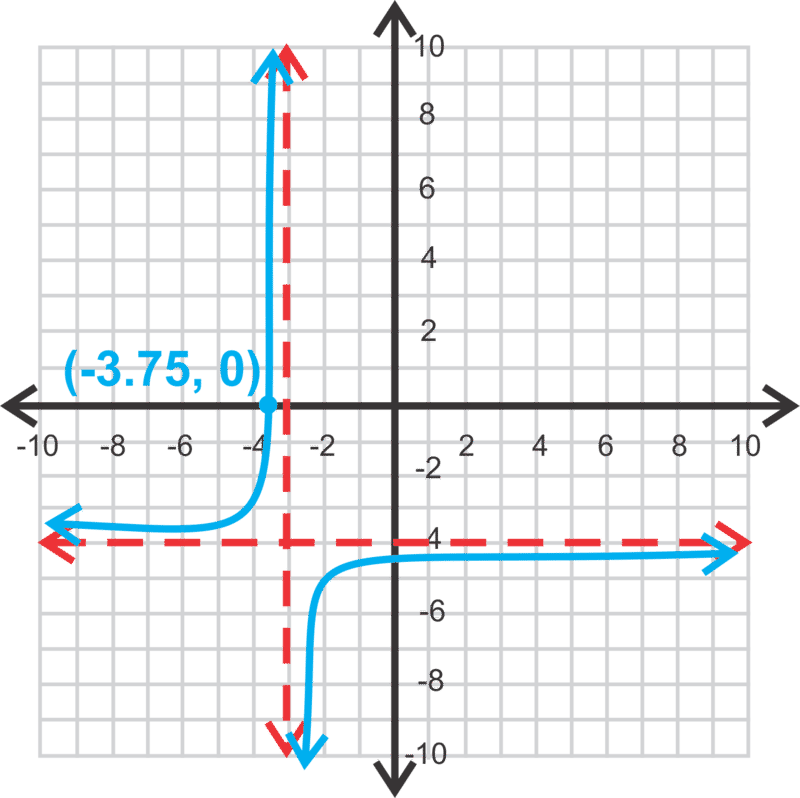
  ::最后,让我们来看看下面的双倍波拉的方程式。

  播放段落

  We know that the numerator will be negative because the branches of this hyperbola are in the second and fourth quadrants. The asymptotes are $\begin{array}{r}x=-3\end{array}$ and $\begin{array}{r}y=-4\end{array}$ . So far, we know $\begin{array}{r}y=\frac{a}{x+3}-4\end{array}$ . In order to determine $\begin{array}{r}a\end{array}$ , we can use the given $\begin{array}{r}x\end{array}$ -intercept.
  ::我们知道,分子将是负数,因为这个超大波拉的分支位于第二和第三四象限。 微粒是 x3 和 y4。 到目前为止, 我们了解 y= ax+3-4。 为了确定一个, 我们可以使用给定的 x 接口 。

  

  播放段落

  $$\begin{array}{rl}0& =\frac{a}{-3.75+3}-4\\ 4& =\frac{a}{-0.75}& & \text{The equation is}y=\frac{-3}{x+3}-4\\ -3& =a\end{array}$$

  
  ::0=3.75+3-44=a-0.75 等式为 y3x+3-4-4-3=a

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to find the asymptotes of the equation  $\begin{array}{r}f(x)=\frac{a}{x-h}+k\end{array}$ . 
  ::早些时候,您被要求找到公式 f( x) = ax-h+k 的微数 。

  播放段落

  From the previous problems , we've seen that the vertical asymptote occurs when the denominator of the equation equals zero and the horizontal asymptote occurs when the range is undefined.
  ::从先前的问题来看,我们已经看到,当方程的分母等于零时,垂直的零点即发生,而水平的零点即发生,当范围未定义时。

  播放段落

  When $\begin{array}{r}x=h\end{array}$ , the denominator of $\begin{array}{r}f(x)=\frac{a}{x-h}+k\end{array}$ is zero, so $\begin{array}{r}x=h\end{array}$ is the vertical asymptote.
  ::当 x=h 时, f( x) = ax-h+k 的分母为零, 所以 x=h 是垂直静态 。

  播放段落

  The value of the function at $\begin{array}{r}x=h\end{array}$ would be $\begin{array}{r}y=\frac{a}{0}+k\end{array}$ , making the range undefined at $\begin{array}{r}y=k\end{array}$ . Therefore, $\begin{array}{r}y=k\end{array}$ is the horizontal asymptote.
  ::x=h 函数的值为 y=a0+k, 使范围在 y=k 未定义。 因此, y=k 是水平单数 。

  播放段落

  Example 2
  ::例2

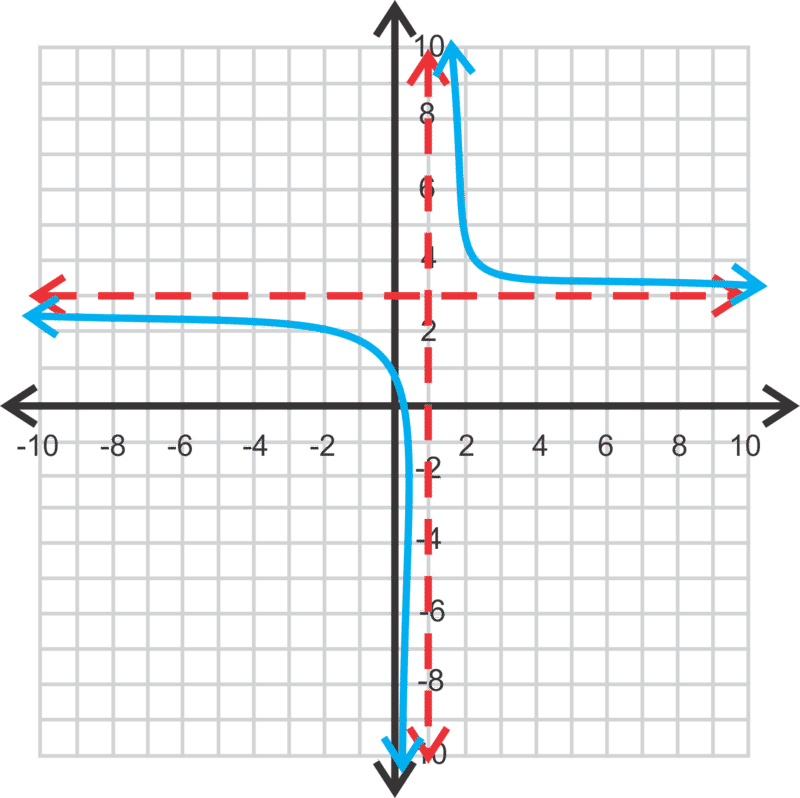
  播放段落

  What are the asymptotes for $\begin{array}{r}f(x)=\frac{-1}{x+6}+9\end{array}$ ? Is $\begin{array}{r}(-5,-8)\end{array}$ on the graph?
  ::f( x)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\F\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\图。

  播放段落

  The asymptotes are $\begin{array}{r}x=-6\end{array}$ and $\begin{array}{r}y=9\end{array}$ . To see if the point $\begin{array}{r}(-5,-8)\end{array}$ is on the graph, substitute it in for $\begin{array}{r}x\end{array}$ and $\begin{array}{r}y\end{array}$ .
  ::秒数为 x+++6 和 y=9 。 要查看点 (-5- 8) 是否在图中, 请将其替换为 x 和 y 。

  播放段落

  $$\begin{array}{rlrl}-8& =\frac{-1}{-5+6}+9& & -8\ne 8,\text{therefore, the point}(-5,-8)\text{is not on the graph}.\\ -8& =-1+9\end{array}$$

  
  ::-8*1-5+6+9-8_8,因此,该点(-5-8)不在图中。

  播放段落

  For Examples 3 & 4, graph  the rational functions. Find the zero, $\begin{array}{r}y\end{array}$ -intercept, asymptotes, domain and range.
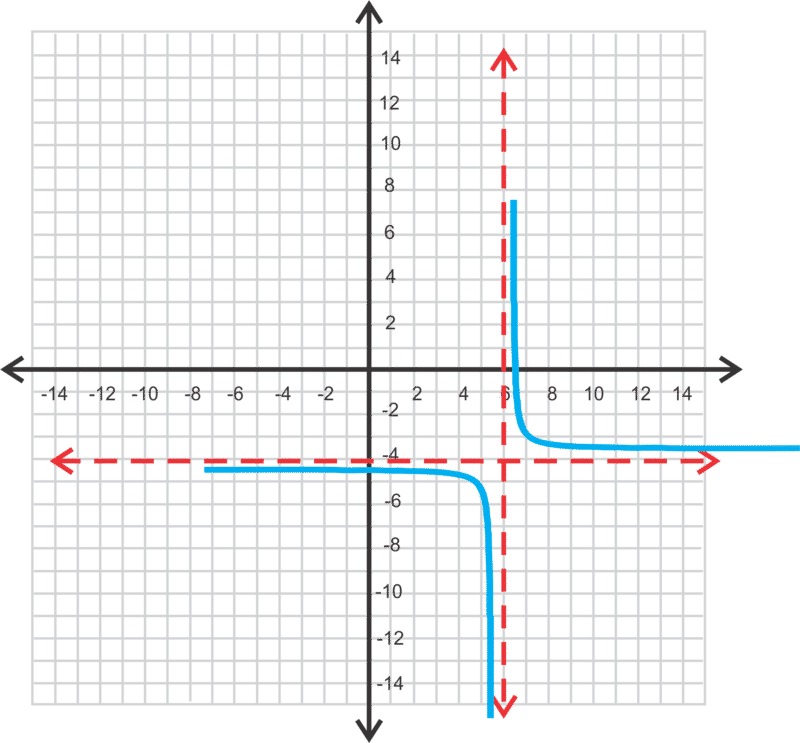
  ::示例 3 和 4 , 图形显示合理函数。 查找 0 、 y interfict、 asymptotes、 域和范围 。

  播放段落

  Example 3
  ::例3

  播放段落

  $\begin{array}{r}y=\frac{4}{x}-2\end{array}$
  ::y=4x-2

  播放段落

  There is no $\begin{array}{r}y\end{array}$ -intercept because the $\begin{array}{r}y\end{array}$ -axis is an asymptote. The other asymptote is $\begin{array}{r}y=-2\end{array}$ . The domain is all real numbers; $\begin{array}{r}x\ne 0\end{array}$ . The range is all real numbers; $\begin{array}{r}y\ne -2\end{array}$ . The zero is:
  ::不存在 Y 界面, 因为 Y 轴是一个小数点。 另一个小数点是 y 。 2 。 域名是全部真实数字; x 0。 范围是全部真实数字; y = 2 。 零是 :

  

  播放段落

  $$\begin{array}{rl}0& =\frac{4}{x}-2\\ 2& =\frac{4}{x}\\ 2x& =4\\ x& =2\end{array}$$

  
  ::0=4x-22=4x2x=4x=2

  播放段落

  Example 4
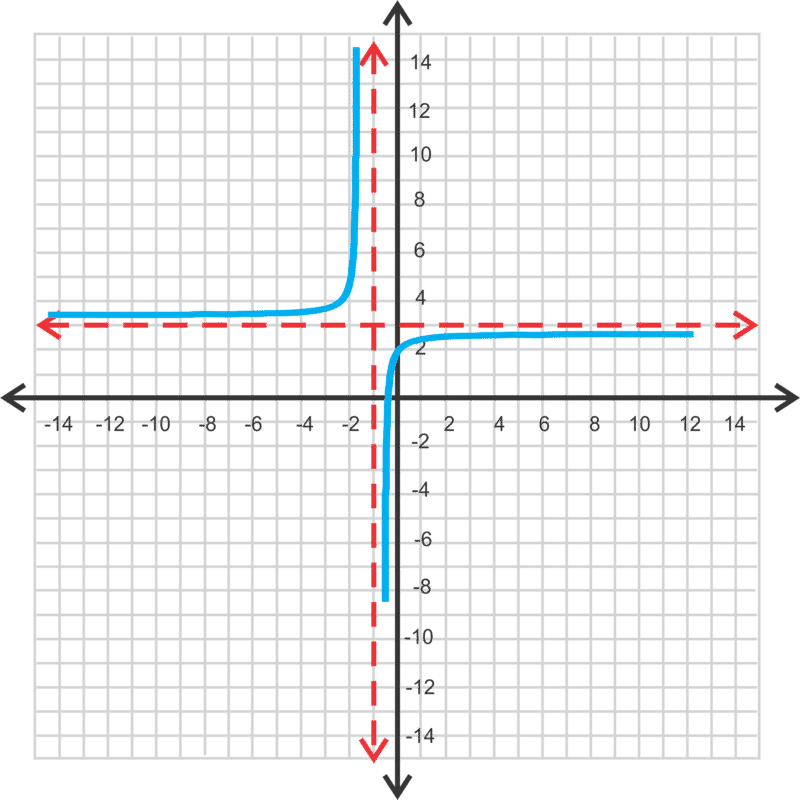
  ::例4

  播放段落

  $\begin{array}{r}y=\frac{2}{x-1}+3\end{array}$
  ::y=2x-1+3 y=2x-1+3

  播放段落

   The asymptotes are $\begin{array}{r}x=1\end{array}$ and $\begin{array}{r}y=3\end{array}$ . Therefore, the domain is all real numbers except 1 and the range is all real numbers except 3. The $\begin{array}{r}y\end{array}$ -intercept is $\begin{array}{r}y=\frac{2}{0-1}+3=-2+3=1\end{array}$ and the zero is:
  ::asymptotes 是 x=1 和 y=3。 因此, 域名是除 1 外的所有真实数字, 范围是除 3 外的所有真实数字 。 y 界面是 y= 20 - 1+3+2+3=1, 零是 :

  

  播放段落

  $$\begin{array}{rl}0& =\frac{2}{x-1}+3\\ -3& =\frac{2}{x-1}\\ -3x+3& =2\\ -3x& =-1\to x=\frac{1}{3}\end{array}$$

  
  ::0=2x-1-1+3-3=2x-1-3x+3=2-3x=3x1xx1x=13

  播放段落

  Example 5
  ::例5

  播放段落

  Determine the equation of the hyperbola.
  ::确定双曲线的方程。

  

  播放段落

  The asymptotes are $\begin{array}{r}x=-1,y=3,\end{array}$ making the equation $\begin{array}{r}y=\frac{a}{x+1}+3\end{array}$ . Taking the $\begin{array}{r}y\end{array}$ -intercept, we can solve for $\begin{array}{r}a\end{array}$ .
  ::年数为 x1,y=3, 方程式为 y=ax+1+3。 使用 Y 界面, 我们可以解答一个 。

  播放段落

  $$\begin{array}{rlrl}4& =\frac{a}{0+1}+3& & \text{The equation is}y=\frac{1}{x+1}+3.\\ 1& =a\end{array}$$

  
  ::4=a0+1+3 此方程式为y=1x+1+1+3.1=a

  播放段落

  Review
  ::回顾

  播放段落
  1. What are the asymptotes for $\begin{array}{r}y=\frac{2}{x+8}-3\end{array}$ ?
     ::y= 2x+8- 3 的年数是多少 ?
  播放段落
  2. Is $\begin{array}{r}(-6,-2)\end{array}$ a point on the graph from #1?
     ::图表上( - 6 - 2) 是否来自 # 1 的点 ?
  播放段落
  3. What are the asymptotes for $\begin{array}{r}y=6-\frac{1}{x-4}\end{array}$ ?
     ::y= 6 - 1x - 4 的年数是多少 ?
  播放段落
  4. Is $\begin{array}{r}(5,4)\end{array}$ a point on the graph from #3?
     :5,4)是3号图上的一个点吗?

  播放段落

  For problems 5-13, graph each rational function, state the equations of the asymptotes, the domain and range and the intercepts.
  ::对于问题5-13, 绘制每个合理函数的图表, 说明小行星的方程、 域域和范围以及拦截的方程 。

  播放段落
  5. $\begin{array}{r}y=\frac{3}{x}\end{array}$
     ::y=3x y=3x
  播放段落
  6. $\begin{array}{r}y=\frac{1}{x}+6\end{array}$
     ::y=1x+6 y=1x+6
  播放段落
  7. $\begin{array}{r}y=-\frac{1}{x}\end{array}$
     ::y1x
  播放段落
  8. $\begin{array}{r}y=-\frac{1}{x+3}\end{array}$
     ::y1x+3 y1x+3
  播放段落
  9. $\begin{array}{r}y=\frac{1}{x+5}\end{array}$
     ::y=1x+5 y=1x+5
  播放段落
  10. $\begin{array}{r}y=\frac{1}{x-3}-4\end{array}$
      ::y= 1x-3- 4 y= 1x- 3- 4
  播放段落
  11. $\begin{array}{r}y=\frac{2}{x+4}-3\end{array}$
      ::y=2x+4-3
  播放段落
  12. $\begin{array}{r}y=\frac{5}{x}+2\end{array}$
      ::y=5x+2 y=5x+2
  播放段落
  13. $\begin{array}{r}y=3-\frac{1}{x+2}\end{array}$
      ::y=3 - 1x+2

  播放段落

  Write the equations of the hyperbolas. You may assume that a = 1.
  ::写出双倍方程式的方程。 您可以假设一个= 1 。

  14. 
  15. 

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。