9.5 数字度和分数度为同时的图形绘制

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 当数值和分数度为相同时的图形图形

  Collapse Expand

  当数值和分数度为相同时的图形图形

  播放段落

  Darnell says that the function $\begin{align*}y=\frac{2x^4+5}{x^4-16}\end{align*}$ has two vertical asymptotes , Barb says it has only one, and Aruna says it has four. Which one of them is correct?
  ::Darnell 说 y= 2x4+5x4- 16 函数有两个垂直微粒, Barb 说它只有一个, Aruna 说它有四个。 其中哪一个是正确的 ?

  播放段落

  Graphing Rational Functions
  ::图形推理函数

  播放段落

  W e have already graphed functions in the form $\begin{align*}y=\frac{1}{x-h}+k\end{align*}$ , where $\begin{align*}x = h\end{align*}$ and $\begin{align*}y = k\end{align*}$ are the asymptotes. In this concept, we will extend graphing rational functions when both the denominator and numerator are linear or both quadratic. So, there will be no “ $\begin{align*}k\end{align*}$ ” term in this concept. Let’s go through some practice problems  to determine any patterns in graphing this type of rational function.
  ::我们已经以 y=1x-h+k 的形式绘制了函数图示, 其中 x=h 和 y=k 是 asymptotes 。 在这个概念中, 当分母和分子都是线性或二次函数时, 我们将会扩展理性函数图示。 因此, 这个概念中不会有“ k” 词。 让我们通过一些实践问题来确定图形显示这种理性函数的任何模式 。

  播放段落

  Let's graph $\begin{align*}f(x)=\frac{2x-1}{x+4}\end{align*}$  and find asymptotes, $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ intercepts , domain and range .
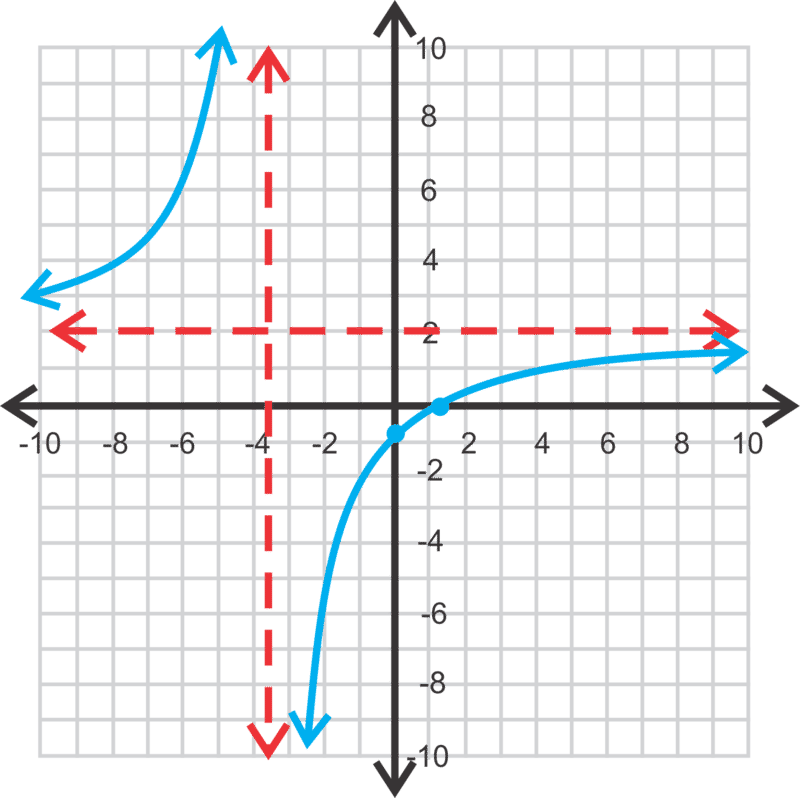
  ::将图形 f( x) = 2x- 1x+ 4 并查找 asymptotes, x 和 y 拦截、 域和范围 。

  播放段落

  To find the vertical asymptote , it is the same as before, the value that makes the denominator zero. In this case, $\begin{align*}x = -4\end{align*}$ . Also the same is how to find the $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ intercepts.
  ::要找到垂直零位数, 和以前一样, 使分母为零的值。 在这种情况下, x+++4 。 如何找到 x 和 y 拦截也是一样的 。

  播放段落

  $\begin{align*}y\end{align*}$ - intercept (when $\begin{align*}x = 0\end{align*}$ ): $\begin{align*}y=\frac{2 \cdot 0-1}{0+4}=- \frac{1}{4}\end{align*}$
  ::y 拦截( 当 x=0 时 ) : y= 20 - 10+4 @ 14

  播放段落

  $\begin{align*}x\end{align*}$ -intercept (when $\begin{align*}y = 0\end{align*}$ ):

  $$\begin{align*}0&=\frac{2x-1}{x+4} \\ 0&=2x-1 \\ 1&=2x \\ \frac{1}{2}&=x\end{align*}$$
  ::x 拦截( 当y=0 时): 0= 2x- 1x+40= 2x- 11= 2x12=x

  播放段落

  When solving for the $\begin{align*}x\end{align*}$ -intercept, to get the denominator out, we multiplied both sides by $\begin{align*}x + 4\end{align*}$ . But, when we multiply anything by 0, it remains 0. Therefore , to find the $\begin{align*}x\end{align*}$ -intercept, we only need to set the numerator equal to zero and solve for $\begin{align*}x\end{align*}$ .
  ::当解析 X 接口时, 要将分母取出, 我们将两边乘以 x+4 。 但是, 当我们乘以 0. 0 时, 它仍然是 0 。 因此, 要找到 x 接口, 我们只需要将分子设置为 0 和 x 的解答 。

  播放段落

  The last thing to find is the horizontal asymptote . We know that the function is positive, so the branches will be in the first and third quadrants . Let’s make a table.
  ::最后要找到的是水平零点。 我们知道这个功能是正的, 因此分支将位于第一和第二四位数。 让我们来做一张桌子。

  $\begin{align*}x\end{align*}$	$\begin{align*}y\end{align*}$
  $\begin{align*}-13\end{align*}$	3
  $\begin{align*}-7\end{align*}$	5
  $\begin{align*}-5\end{align*}$	11
  $\begin{align*}-3\end{align*}$	$\begin{align*}-7\end{align*}$
  $\begin{align*}-1\end{align*}$	$\begin{align*}-1\end{align*}$
  0	$\begin{align*}-0.25\end{align*}$
  2	0.5
  5	1
  14	1.5

  播放段落

  It looks like the horizontal asymptote is $\begin{align*}y = 2\end{align*}$ because both branches seem to approach 2 as $\begin{align*}x\end{align*}$ gets larger, both positive and negative. If we plug in $\begin{align*}x = 86, y = 1.9\end{align*}$ and when $\begin{align*}x = -94, y = 2.1\end{align*}$ . As you can see, even when $\begin{align*}x\end{align*}$ is very large, the function is still approaching 2.
  ::看起来水平的零点为 y=2, 因为两个分支似乎都接近 2 , 因为 x 越大, 正值和负值。 如果我们插入 x=86,y=1. 9 和 x\\\ 94,y= 2. 1。 正如您所看到的, 即使 x 很大, 该函数仍然接近 2 。

  

  播放段落

  Looking back at the original equation , $\begin{align*}f(x)= \frac{2x-1}{x+4}\end{align*}$ , extract the leading coefficients and leave them numerator over denominator, $\begin{align*}\frac{2}{1}\end{align*}$ . This is the horizontal asymptote. We can generalize this pattern for all rational functions. When the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is the ratio of the leading coefficients.
  ::回顾原来的方程, f( x) = 2x- 1x+4, 提取主要系数, 并留置分子在分母上方的位数, 21。 这是水平的同位数。 我们可以对所有理性函数都使用这个模式。 当分子的程度等于分母的程度时, 水平的同位数是主要系数的比 。

  播放段落

  Finally, the domain is all real numbers; $\begin{align*}x \ne -4\end{align*}$ and the range is all real numbers; $\begin{align*}y \ne 2\end{align*}$ .
  ::最后,域名是全部真实数字; x4, 范围是全部真实数字; y2。

  播放段落

  Now, let's graph $\begin{align*}y=\frac{3x^2+10}{x^2-1}\end{align*}$  and find the asymptotes, intercepts, domain, and range.
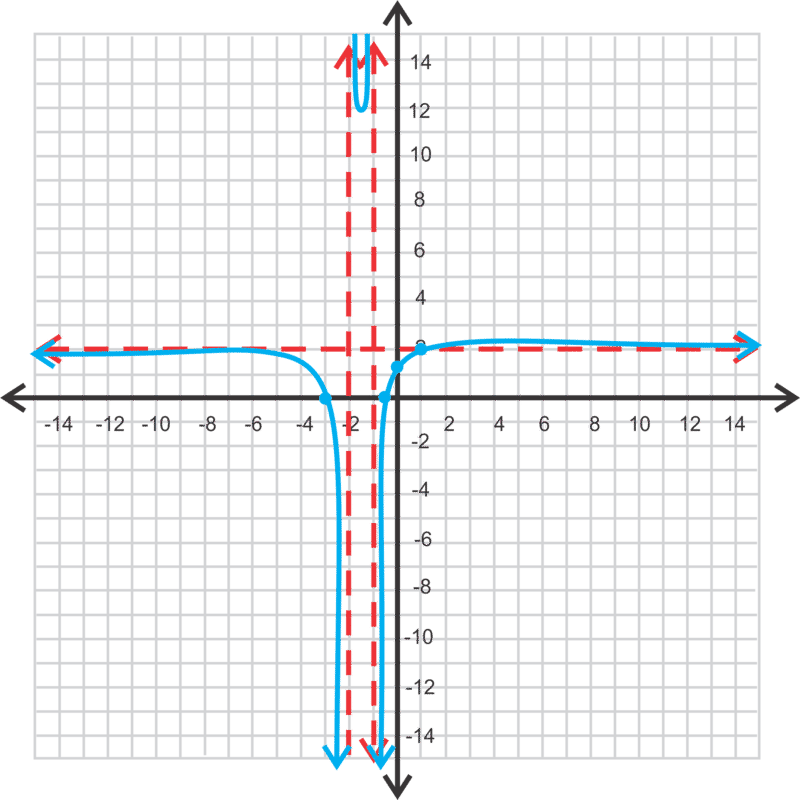
  ::现在,让我们来绘制 y= 3x2+10x2- 1, 并找到小数点、 拦截、 域和范围 。

  播放段落

  From the previous problem above , we can conclude that the horizontal asymptote is at $\begin{align*}y = 3\end{align*}$ . Because the denominator is squared, there will be two vertical asymptotes because $\begin{align*}x^2-1\end{align*}$ factors to $\begin{align*}(x - 1)(x + 1)\end{align*}$ . Therefore, the vertical asymptotes are $\begin{align*}x = 1\end{align*}$ and $\begin{align*}x = -1\end{align*}$ . As for the intercepts, there are no $\begin{align*}x\end{align*}$ -intercepts because there is no real solution for $\begin{align*}3x^2+10=0\end{align*}$ . Solving for the $\begin{align*}y\end{align*}$ -intercept, we have $\begin{align*}y=\frac{10}{-1}=-10\end{align*}$ .
  ::从上述前一个问题中,我们可以得出结论,水平小数是在 y=3 。 因为分母是正方的, 将有两个垂直小数, 因为 x2-1 系数到 (x-1)(x+1) 。 因此, 垂直小数是 x=1 和 x1 。 至于拦截, 没有 X 拦截, 因为 3x2+10=0 没有真正的解决方案 。 为 y 界面解析, 我们有 y= 10 - 1\\ 10 。

  播放段落

  At this point, put the equation in your calculator to see the general shape. To graph this function using a TI-83 or 84, enter the function into $\begin{align*}Y=\end{align*}$ like this: $\begin{align*}\frac{\left(3x^\land2+10\right)}{\left(x^\land2-1\right)}\end{align*}$ and press GRAPH . You will need to expand the window to include the bottom portion of the graph. The final graph is below.
  ::在此点, 请在您的计算器中设置方程式以查看一般形状。 要用 TI- 83 或 84 绘制此函数图, 请输入Y= 的函数 : (3x2+10) (x2- 1) 并按 GRAPH 键。 您需要扩大窗口以包含图形的底部部分 。 最后的图表在下面 。

  

  播放段落

  The domain is still all real numbers except the vertical asymptotes. For this function, that would be all real numbers; $\begin{align*}x \ne -1,x \ne 1\end{align*}$ .
  ::域名仍然是所有真实数字,除了垂直的静态数。对于此函数,所有真实数字都是; x1,x1。

  播放段落

  The range is a bit harder to find. Notice the gap in the range from the horizontal asymptote and the $\begin{align*}y\end{align*}$ -intercept. Therefore, the range is $\begin{align*}(- \infty, -10] \cup (3,\infty)\end{align*}$ .
  ::范围比较难查找。 注意从水平渐渐断开和 y- intercut 之间的距离差。 因此, 范围是 (, ~ 10) \\ \ (3, ) 。

  播放段落

  The notation above is one way to write a range of numbers called interval notation and was already introduced .  The $\begin{align*}\cup\end{align*}$ symbol means “ union .” Notice that $\begin{align*}- \infty\end{align*}$ and $\begin{align*}\infty\end{align*}$ are not included in the range.
  ::上面的注解是写出一系列数字的一种方式,这些数字被称为间距符号, 并且已经引入。 符号意指“ 工会 ” 。 请注意 和 不属于此范围 。

  播放段落

  In general, rational functions with quadratics in the denominator are split into six regions and have branches in three of them, like the problem  above. However, there are cases when there are no zeros or vertical asymptotes and those look very different. You should always graph the function in a graphing calculator after you find the critical values and make as accurate a sketch as you can.
  ::一般而言,分母中带有二次方位的理性函数分为六个区域,并在其中三个区域中设有分支,如上述问题。但是,有些情况下,没有零或垂直静态,而且这些功能看起来非常不同。在找到关键值并尽可能准确地绘制草图之后,你总是应该在图形计算器中绘制该函数的图形。

  播放段落

  Finally, let's graph $\begin{align*}f(x)=\frac{x^2-8x+12}{x^2-x-6}\end{align*}$  and find the intercepts, asymptotes, domain and range.
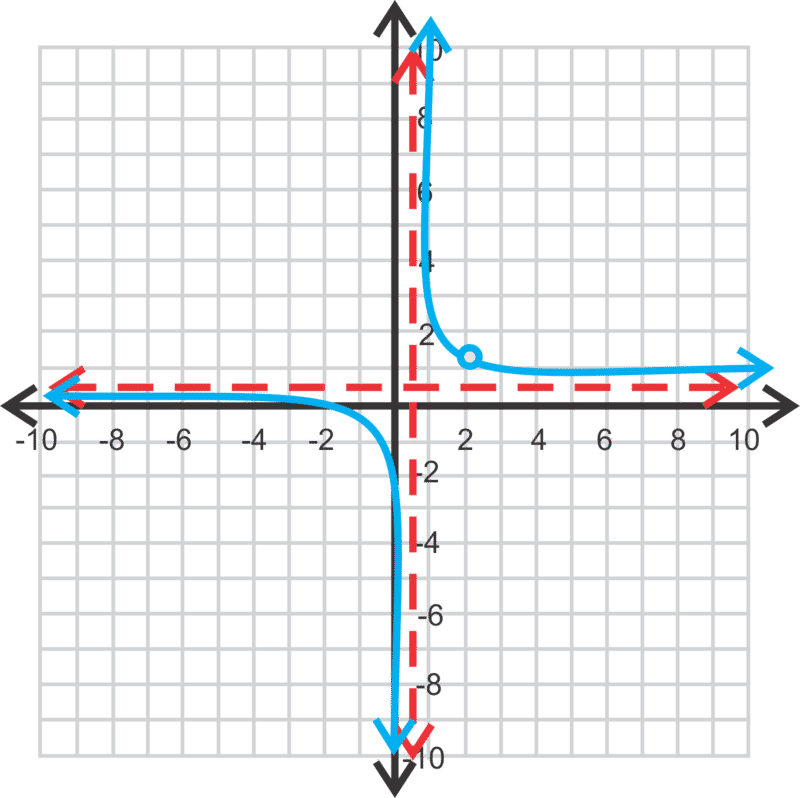
  ::最后,让我们将f(x) =x2-8x+12x2-x-6 图形查找拦截物、 微粒、 域和范围。

  播放段落

  Let’s factor the numerator and denominator to find the intercepts and vertical asymptotes.
  ::让我们将分子和分母乘以找到拦截物和垂直静态。

  播放段落

  $\begin{align*}f(x)=\frac{x^2-8x+12}{x^2+x-6}=\frac{\left(x-6\right) \left(x-2\right)}{\left(x+3\right) \left(x-2\right)}\end{align*}$
  :x) =x2-8x+12x2+x-6=(x-6)(x-2)(x+3)(x-2)

  播放段落

  Notice that the numerator and denominator both have a factor of $\begin{align*}(x - 2)\end{align*}$ . When this happens, a hole is created because $\begin{align*}x = 2\end{align*}$ is both a zero and an asymptote. Therefore, $\begin{align*}x = 2\end{align*}$ is a hole and neither a zero nor an asymptote.
  ::注意分子和分母都有( x-2 ) 系数, 当发生这种情况时, 因为 x=2 既是一个零又是一个小数点, 所以会创建一个洞。 因此, x=2 是一个洞, 既不是零, 也不是零 。

  

  播放段落

  There is a vertical asymptote at $\begin{align*}x = -3\end{align*}$ and a zero at $\begin{align*}x = 6\end{align*}$ . The horizontal asymptote is at $\begin{align*}y = 1\end{align*}$ . The graph of $\begin{align*}f(x)=\frac{x^2-8x+12}{x^2-x-6}\end{align*}$ will look like the graph of $\begin{align*}f(x)=\frac{x-6}{x+3}\end{align*}$ , but with a hole at $\begin{align*}x = 2\end{align*}$ . A hole is not part of the domain. And, the output value that corresponds with the hole is not part of the range. In this problem , $\begin{align*}f(2)=\frac{2-6}{2+3}=\frac{-4}{6}=- \frac{2}{3}\end{align*}$ is not part of the range. If you were to graph this function on your graphing calculator, the calculator would not show there is a hole.
  ::在 x3 和 x=6 上有一个垂直的单点点, 在 x=6 上有一个零。 水平的单点点在y=1 。 f( x) =x2- 8x+12x2-x2- x- 6x-6 的图形将看起来像 f( x) =x-6x+3 的图形, 但是在 x=2 上有一个洞。 空洞不是域的一部分。 与空洞相对应的输出值不是范围的一部分。 在此问题中, f(2)=2- 62+3+_ @ 146} 23 不属于范围的一部分。 如果您要在您的图形计算器上显示此函数, 计算器将不会显示有空洞 。

  播放段落

  The domain is $\begin{align*}x \in \mathbb{R};x \ne 2,-3\end{align*}$ and the range is $\begin{align*}y \in \mathbb{R};y \ne 1,- \frac{2}{3}\end{align*}$ .
  ::域名是 xR; x2; - 3, 范围是yR;y1;- 23。

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to determine which student  is correct. 
  ::早些时候,有人要求你确定哪个学生是正确的。

  播放段落

  The vertical asymptote(s) occur(s) when the denominator of the function equals zero. For the function $\begin{align*}y=\frac{2x^4+5}{x^4-16}\end{align*}$ , the denominator equals zero when $\begin{align*}x^4-16 = 0\end{align*}$ .
  ::当函数的分母等于零时,则出现垂直数。对于函数 y= 2x4+5x4-16, 当 x4- 16=0时, 分母等于零 。

  播放段落

  $$\begin{align*} x^4-16 = 0 \\ x^4 = 16\end{align*}$$
  ::x4 - 16=0x4=16

  播放段落

  $\begin{align*}x = 2\end{align*}$ or $\begin{align*}x = -2\end{align*}$
  ::x=2 或 x2

  播放段落

  Therefore, there are two vertical asymptotes and Darnell is correct.
  ::因此,有两条垂直的静态,达内尔是正确的。

  播放段落

  Graph the following functions. Find all intercepts, asymptotes, the domain and range. Double-check your answers with a graphing calculator.
  ::图形 如下函数。 查找所有拦截、 asymptotes、 域和范围。 用图形计算器双倍检查您的答案 。

  播放段落

  Example 2
  ::例2

  播放段落

  $\begin{align*}y=\frac{4x-5}{2x+7}\end{align*}$
  ::y=4x-52x+7 y=4x-52x+7

  播放段落

  $\begin{align*}y\end{align*}$ -intercept: $\begin{align*}y=\frac{-5}{7}=- \frac{5}{7}\end{align*}$ , $\begin{align*}x\end{align*}$ -intercept: $\begin{align*}0=4x-5 \rightarrow x=\frac{5}{4}\end{align*}$ , horizontal asymptote: $\begin{align*}y=\frac{4}{2}=2\end{align*}$ , vertical asymptote: $\begin{align*}2x+7=0 \rightarrow x=- \frac{7}{2}\end{align*}$ , domain: $\begin{align*}\mathbb{R};x \ne - \frac{7}{2}\end{align*}$ , range: $\begin{align*}\mathbb{R};y \ne 2\end{align*}$
  ::y 截取 : y5757, x 截取: 0=4x- 5x=54, 水平吸附: y=42=2, 垂直吸附: 2x+7=0x72, 域名: R; x72, 范围: R;y2

  

  播放段落

  Example 3
  ::例3

  播放段落

  $\begin{align*}f(x)=\frac{x^2-9}{x^2+1}\end{align*}$
  :xx) =x2- 9x2+1

  播放段落

  $\begin{align*}y\end{align*}$ -intercept: $\begin{align*}y=\frac{-9}{1}=-9\end{align*}$ , $\begin{align*}x\end{align*}$ -intercepts: $\begin{align*}0=x^2-9 \rightarrow x= \pm 3\end{align*}$ , horizontal asymptote: $\begin{align*}y=1\end{align*}$ , vertical asymptote: none, domain: $\begin{align*}\mathbb{R}\end{align*}$ , range: $\begin{align*}\mathbb{R};y \ne 1\end{align*}$
  ::y 截取 : y919, x 截取 : 0=x2- 9x3, 水平渐移: y=1, 垂直渐移: 否, 域 : R, 范围: R;y1

  播放段落

  Special Note: When there are no vertical asymptotes and the numerator and denominator are both quadratics, this is the general shape. It could also be reflected over the horizontal asymptote.
  ::特别说明:当没有垂直静脉微粒时,当分子和分母都是二次方形时,这就是一般形状。也可以在水平静脉微粒上反射。

  

  播放段落

  Example 4
  ::例4

  播放段落

  $\begin{align*}y=\frac{2x^2+7x+3}{x^2+3x+2}\end{align*}$
  ::y= 2x2+7x+3x2+3x2+2

  播放段落

  $\begin{align*}y\end{align*}$ -intercept: $\begin{align*}\left(0, \frac{3}{2}\right)\end{align*}$ , $\begin{align*}x\end{align*}$ -intercepts: $\begin{align*}(-3,0)\end{align*}$ and $\begin{align*}\left(- \frac{1}{2},0\right)\end{align*}$ , horizontal asymptote: $\begin{align*}y = 2\end{align*}$ , vertical asymptotes: $\begin{align*}x = -2, x = -1\end{align*}$ .
  ::y 拦截: (0,32), x 拦截-3,0) 和 (- 12,0), 水平停止: y= 2, 垂直停止: x2, x 1 。

  播放段落

  domain: $\begin{align*}\mathbb{R};x \ne -1,-2\end{align*}$
  ::域名: R; x%1, - 2

  播放段落

  range: $\begin{align*}y \in (- \infty,2.1] \cup [12, \infty)\end{align*}$
  ::区域:y(,2.1)][12,]

  

  播放段落

  Example 5
  ::例5

  播放段落

  $\begin{align*}y=\frac{x^2-4}{2x^2-5x+2}\end{align*}$
  ::y=x2 - 42x2 - 5x+2

  播放段落

  horizontal asymptote: $\begin{align*}y=\frac{1}{2}\end{align*}$ , $\begin{align*}y\end{align*}$ -intercept: $\begin{align*}(0,-2)\end{align*}$
  ::水平空点 : y=12, y- 界面 : (0) ~ 2

  播放段落

  vertical asymptotes: $\begin{align*}x=\frac{1}{2}\end{align*}$ , $\begin{align*}x\end{align*}$ -intercept: $\begin{align*}(-2,0)\end{align*}$
  ::垂直空点数: x=12, x 界面-2,0)

  播放段落

  hole: $\begin{align*}x = 2, f(2)=\frac{4}{3}\end{align*}$
  ::空格: x=2, f(2)=43

  播放段落

  domain: $\begin{align*}\mathbb{R};x \ne \frac{1}{2},2\end{align*}$
  ::域名: R;x%12,2

  播放段落

  range: $\begin{align*}\mathbb{R};y \ne \frac{1}{2}, \frac{4}{3}\end{align*}$
  ::范围: R; y12, 43

  

  播放段落

  Review
  ::回顾

  播放段落
  1. What are the vertical and horizontal asymptotes for $\begin{align*}y=\frac{x-2}{x+7}\end{align*}$ ?
     ::Y=x- 2x+7 的垂直和水平等量值是什么 ?
  播放段落
  2. What is the domain of this function?
     ::此函数的域是什么 ?
  播放段落
  3. What is the range of this function?
     ::此函数的范围是什么?
  播放段落
  4. Are there any x -intercepts? If so, what are they?
     ::是否有X拦截器?如果有,它们是什么?
  播放段落
  5. Is there a y -intercept? If so, what is it?
     ::如果有,那是什么?

  播放段落

  Graph the following rational functions. Write down the equations of the asymptotes, the domain and range, $\begin{align*}x\end{align*}$ and $\begin{align*}y\end{align*}$ intercepts and identify any holes.
  ::绘制以下合理函数的图形。写下小数方程式、域和范围、 x 和 y 拦截,并识别任何洞。

  播放段落
  6. $\begin{align*}y=\frac{x+3}{x-5}\end{align*}$
     ::y=x+3x- 5 y=x+3x- 5
  播放段落
  7. $\begin{align*}y=\frac{5x+2}{x-4}\end{align*}$
     ::y= 5x+2x- 4
  播放段落
  8. $\begin{align*}y=\frac{3-x}{2x+10}\end{align*}$
     ::y=3 - x2x+10 y=3 - x2x+10
  播放段落
  9. $\begin{align*}y=\frac{x^2+5x+6}{x^2-8x+12}\end{align*}$
     ::y=x2+5x+6x2_8x+12
  播放段落
  10. $\begin{align*}y=\frac{x^2+4}{2x^2+x-3}\end{align*}$
      ::y=x2+42x2+x-3 y=x2+42x2+x-3
  播放段落
  11. $\begin{align*}y=\frac{2x^2-x-10}{3x^2+10x+8}\end{align*}$
      ::y=2x2 - x - 103x2+10x+8
  播放段落
  12. $\begin{align*}y=\frac{x^2-4}{x^2+3x-10}\end{align*}$
      ::y=x2- 4x2+3x- 10
  播放段落
  13. $\begin{align*}y=\frac{6x^2-7x-3}{4x^2-1}\end{align*}$
      ::y= 6x2 - 7x - 34x2 - 1
  播放段落
  14. $\begin{align*}y=\frac{x^3-8}{x^3+x^2-4x-4}\end{align*}$
      ::y=x3 - 8x3+x2 - 4x- 4
  播放段落
  15. Graph $\begin{align*}y=\frac{1}{x-2}+3\end{align*}$ and $\begin{align*}y=\frac{3x-5}{x-2}\end{align*}$ on the same set of axes. Compare the two. What do you notice? Explain your results.
      ::相同轴组上的 y= 1x-2+3 和 y= 3x- 5x-2 。 比较这两个轴组。 您注意到什么 ? 请解释您的结果 。

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。