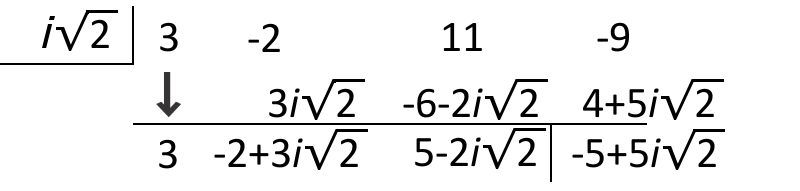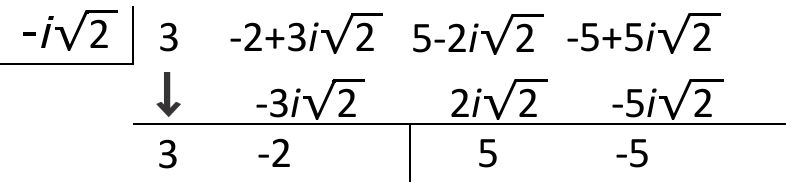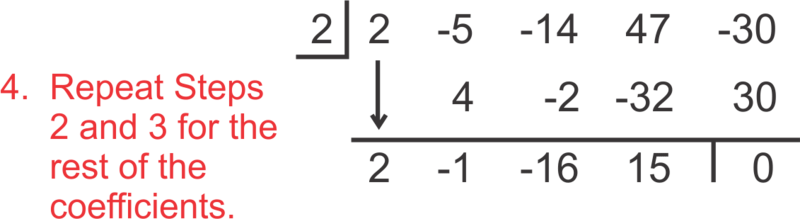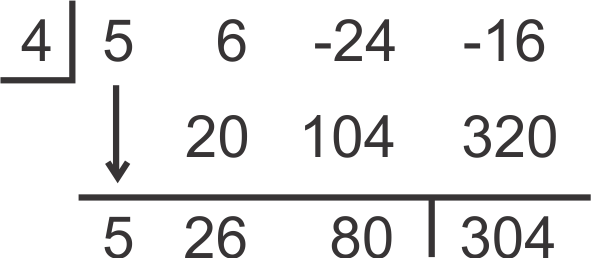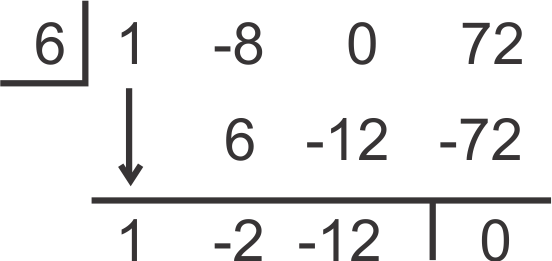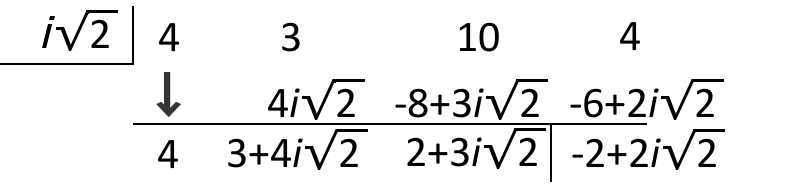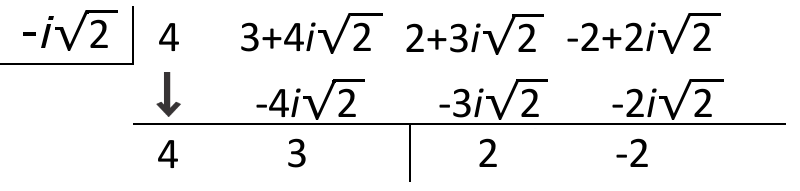Course: 2.11 多项式的综合除法

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 多项式的综合除法

Collapse Expand
多项式的综合除法
If you have completed the lesson on , you probably know that the problem:
::问题在于:

Find the of $\begin{aligned} f (x) = \frac{3 x^{3} - 2 x^{2} + 11 x - 9}{x^{2} + 2} \end{aligned}$
::查找 f( x) = 3x3- 2x2+11x- 9x2+2

could be an excellent reason to groan and grumble due to the long division that would be required.
::这可能是一个极好的理由来呻吟和抱怨，因为需要进行冗长的除法运算。

Isn't there a better way?
::有没有更好的办法?

Synthetic Division of Polynomials
::多项式的综合除法

Synthetic division is an alternative to long division from the previous concept. It can also be used to divide a polynomial by a possible factor , $\begin{aligned} x - k \end{aligned}$ . However, synthetic division cannot be used to divide larger , like quadratics, into another polynomial.
::综合除法是以前概念中长除法的替代方法。它也可以用来用一个多项式除以一个可能的因子，x - k。然而，合成除法不能用于将更大的多项式，比如二次多项式，分解成另一个多项式。

Examples
::实例

Example 1
::例1

Earlier, you were given a question about finding a better way to divide polynomials.
::早些时候,你被问到如何找到更好的方法来分裂多种族。

If we want to use synthetic division, notice that the factor is not in the form
::如果我们想要使用合成分分法,请注意该因素并非以该形式出现。

$\begin{aligned} (x - k) \end{aligned}$ . Therefore , we need to solve the possible factor for zero to see what the possible solution would be. If $\begin{aligned} x^{2} + 2 = 0 \end{aligned}$ , then $\begin{aligned} x = \pm i \sqrt{2} \end{aligned}$ , which can also be expressed as $\begin{aligned} x = + i \sqrt{2} \end{aligned}$ or $\begin{aligned} x = - i \sqrt{2} \end{aligned}$ . Therefore, we need to use synthetic division twice because there are two .
:x-k) 因此,我们需要解决零的可能因子, 以便知道什么是可能的解决方案。如果 x2+2=0, 那么 xi2, 也可以以 xi2 或 x2 表示。因此, 我们需要使用合成分解两次, 因为有两种。

To start, put $\begin{aligned} i \sqrt{2} \end{aligned}$ up in the left-hand corner box.
::首先,把i2放到左手角盒子里

When we perform the synthetic division, we get a remainder of $\begin{aligned} - 5 + 5 i \sqrt{2} \end{aligned}$ .
::当我们执行合成师, 我们得到剩下的5+52。

Next, we divide results from the last synthetic division with the other complex root . Put $\begin{aligned} - i \sqrt{2} \end{aligned}$ up in the left-hand corner box.
::接下来,我们把最后合成分解的结果与其他复杂的根分解。把-i2放在左手角框中。

As a result, $\begin{aligned} f (x) = \frac{3 x^{3} - 2 x^{2} + 11 x - 9}{x^{2} + 2} = 3 x - 2 + \frac{5 x - 5}{x^{2} + 2} \end{aligned}$ .
::因此,f(x)=3x3-2x2+11-9x2+2=3x-2+5x-5x2+2。

Example 2
::例2

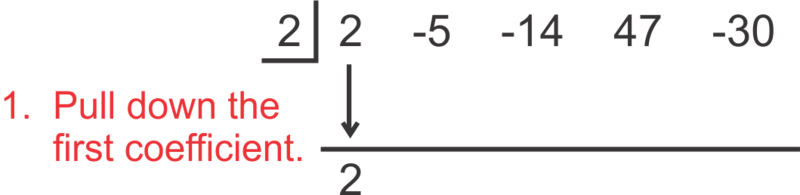
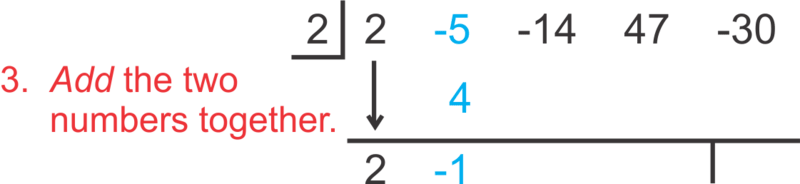
Divide $\begin{aligned} 2 x^{4} - 5 x^{3} - 14 x^{2} + 47 x - 30 \end{aligned}$ by $\begin{aligned} x - 2 \end{aligned}$ .
::将 2x4 - 5x3 - 14x2+47x- 30 除以 x-2 。

Using synthetic division, the setup is as follows:
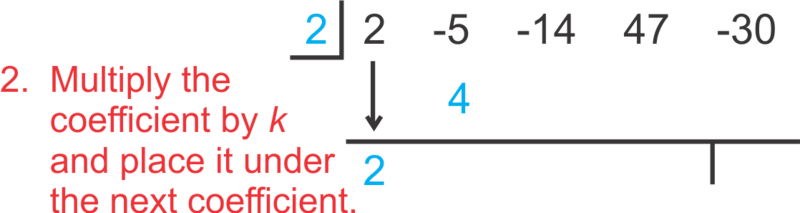
::利用合成部门,设置如下:

To “read” the answer, use the numbers as follows:
::在“阅读”答案时,使用以下数字:

Therefore, 2 is a solution, because the remainder is zero. The factored polynomial is $\begin{aligned} 2 x^{3} - x^{2} - 16 x + 15 \end{aligned}$ . Notice that when we synthetically divide by $\begin{aligned} k \end{aligned}$ , the “leftover” polynomial is one degree less than the original. We could also write $\begin{aligned} (x - 2) (2 x^{3} - x^{2} - 16 x + 15) = 2 x^{4} - 5 x^{3} - 14 x^{2} + 47 x - 30 \end{aligned}$ .
::因此, 2 是一个解决方案, 因为剩余部分为零。系数多元值为 2x3 - x2 - 16x+15。注意当我们合成除以 k 时, “ 剩余” 多元值比原值低一度。我们还可以写入 (x-2)( 2x3 - x2 - 16x+15) = 2x4 - 5x3 - 14x2+47x- 30) 。

Example 3
::例3

Determine if 4 is a solution to $\begin{aligned} f (x) = 5 x^{3} + 6 x^{2} - 24 x - 16 \end{aligned}$ .
::确定 4 是 f( x) = 5x3+6x2 - 24x - 16 的解决方案。

Using synthetic division, we have:
::利用合成分区,我们有:

The remainder is 304, so 4 is not a solution. Notice if we substitute in $\begin{aligned} x = 4 \end{aligned}$ , also written $\begin{aligned} f (4) \end{aligned}$ , we would have $\begin{aligned} f (4) = 5 (4)^{3} + 6 (4)^{2} - 24 (4) - 16 = 304 \end{aligned}$ . This leads us to the Remainder Theorem .
::其余为 304, 因此 4 不是一个解决方案。如果我们替换 x= 4 , 通知将使用 f(4)= 5(4)3+6(4)2- 24(4)- 16= 304。这让我们找到残余理论。

Remainder Theorem: If $\begin{aligned} f (k) = r \end{aligned}$ , then $\begin{aligned} r \end{aligned}$ is also the remainder when dividing by $\begin{aligned} (x - k) \end{aligned}$ .
::保留定理: 如果 f(k) =r, 当除以 (x-k) 时, r 也代表剩余。

This means that if you substitute in $\begin{aligned} x = k \end{aligned}$ or divide by $\begin{aligned} k \end{aligned}$ , what comes out of $\begin{aligned} f (x) \end{aligned}$ is the same. $\begin{aligned} r \end{aligned}$ is the remainder, but it is also the corresponding $\begin{aligned} y - \end{aligned}$ value. Therefore, the point $\begin{aligned} (k, r) \end{aligned}$ would be on the graph of $\begin{aligned} f (x) \end{aligned}$ .
::这意味着,如果您用 x=k 或除以 k 来替代 x=k 或除以 k, f( x) 中产生的内容是相同的。 r 是剩余部分, r 也是相应的 y- value。因此, 点( k,r) 将会在 f( x) 的图形中。

Example 4
::例4

Determine if $\begin{aligned} (2 x - 5) \end{aligned}$ is a factor of $\begin{aligned} 4 x^{4} - 9 x^{2} - 100 \end{aligned}$ .
::确定(2x-5)是否为4x4-9x2-100系数。

If you use synthetic division, the factor is not in the form $\begin{aligned} (x - k) \end{aligned}$ . We need to solve the possible factor for zero to see what the possible solution would be. Therefore, we need to put $\begin{aligned} \frac{5}{2} \end{aligned}$ up in the left-hand corner box. Also, not every term is represented in this polynomial. When this happens, you must put in zero placeholders. In this example, we need zeros for the $\begin{aligned} x^{3} - \end{aligned}$ term and the $\begin{aligned} x - \end{aligned}$ term.
::如果您使用合成除法, 则该因子不是以( x- k) 的形式( x- k) 。我们需要解决零的可能因子, 才能看出可能的解决办法是什么。因此, 我们需要将52 放在左侧角框中。另外, 并非每个术语都代表于此多面体中。发生这种情况时, 您必须输入零占位符。在此示例中, x3- 期和 x- 期中我们需要零。

This means that $\begin{aligned} \frac{5}{2} \end{aligned}$ is a zero and its corresponding binomial , $\begin{aligned} (2 x - 5) \end{aligned}$ , is a factor.
::这意味着52是零,其相应的二进制(2x-5)是一个因素。

Example 5
::例5

Is 6 a solution for $\begin{aligned} f (x) = x^{3} - 8 x^{2} + 72 \end{aligned}$ ? If so, find the real-number zeros (solutions) of the resulting polynomial.
::6 是 f( x) =x3- 8x2+72 的解决方案吗 ? 如果是的话, 请找到结果的多元性的实际数字零( 解决方案) 。

Put a zero placeholder for the $\begin{aligned} x - \end{aligned}$ term. Divide by 6.
::x- 期数设置一个零占位符。除以 6 。

The resulting polynomial is $\begin{aligned} x^{2} - 2 x - 12 \end{aligned}$ . While this quadratic does not factor, we can use the Quadratic Formula to find the other roots.
::由此产生的多面体为 x2-2x-12。虽然此二次方块不因子, 但是我们可以使用二次方块来找到其他根。

$\begin{aligned} x = \frac{2 \pm \sqrt{2^{2} - 4 (1) (- 12)}}{2} = \frac{2 \pm \sqrt{4 + 48}}{2} = \frac{2 \pm 2 \sqrt{13}}{2} = 1 \pm \sqrt{13} \end{aligned}$

::x=222-4(1)(-1-2)2=24+482=22132=113

The solutions to this polynomial are 6, $\begin{aligned} 1 + \sqrt{13} \approx 4.61 \end{aligned}$ and $\begin{aligned} 1 - \sqrt{13} \approx - 2.61 \end{aligned}$ .
::这一多元性的解决办法是6, 1+134.61和1-132.61。

Example 6
::例6

Divide $\begin{aligned} 4 x^{3} + 3 x^{2} + 10 x + 4 \end{aligned}$ by $\begin{aligned} (x^{2} + 2) \end{aligned}$ . Write the resulting polynomial with the remainder (if there is one).
::除以 4x3+3x2+10x+4 乘以 (x2+2) 。

Using synthetic division, divide by $\begin{aligned} i \sqrt{2} \end{aligned}$ .
::使用合成分除法,除以i2。

Divide the results from the last step by $\begin{aligned} - i \sqrt{2} \end{aligned}$ .
::将最后一步的结果除以-i2。

The answer is $\begin{aligned} 4 x + 3 + \frac{2 x - 2}{x^{2} + 2} \end{aligned}$ .
::答案是 4x+3+2x-2x2+2。

Review
::回顾

Divide using synthetic division:
::使用合成分数的除法 :

$\begin{aligned} \frac{7 x^{2} - 23 x + 6}{x - 3} \end{aligned}$
::7x2-23x+6x-3

$\begin{aligned} \frac{x^{4} - 5 x + 10}{x + 3} \end{aligned}$
::x4 - 5x+10x+3

$\begin{aligned} (2 x^{2} + 13 x - 8) \div (x - \frac{1}{2}) \end{aligned}$
:2x2+13x-8)(x-12)

$\begin{aligned} (x^{4} + 6 x^{3} + 6 x^{2}) \div (x + 5) \end{aligned}$
:x4+6x3+6x2) (x+5)

$\begin{aligned} \frac{x^{3} - 7 x - 6}{x + 2} \end{aligned}$
::x3 - 7x - 6x+2

$\begin{aligned} \frac{8 y^{3} + y^{4} + 16 + 32 y + 24 y^{2}}{y + 2} \end{aligned}$
::8y3+y4+16+32y+24y2y+2

Use synthetic substitution to evaluate the polynomial function for the given value:
::使用合成替代来评价给定值的多元函数:

$\begin{aligned} P (x) = 2 x^{2} - 5 x - 3 \end{aligned}$ for $\begin{aligned} x = 4 \end{aligned}$
::x=4的P(x)=2x2-5x-3

$\begin{aligned} P (x) = 4 x^{3} - 5 x^{2} + 3 \end{aligned}$ for $\begin{aligned} x = - 1 \end{aligned}$
::x% 1 的 P(x) = 4x3 - 5x2+3

$\begin{aligned} p (x) = 3 x^{3} - 5 x^{2} - x = 2 \end{aligned}$ for
::p(x) = 3x3 - 5x2 - x= 2 用于

The area of a rectangle is $\begin{aligned} 3 x^{3} - 11 x^{2} - 56 x - 48 \end{aligned}$ and the length is $\begin{aligned} 3 x + 4 \end{aligned}$ . What is the width?
::矩形区域为 3x3 - 11x2 - 56x- 48,长度为 3x+4。宽度是多少?

A group of geologists have taken a collection of samples of a substance from a proposed mining site and must identify the substance. Each sample is roughly cylindrical. The volume of each sample as a function of cylinder height (in centimeters) is %20%3D%20%5Cfrac%20%7B1%7D%7B4%7D%20%5Cpi%20h%5E3"> $\begin{aligned} V (h) = \frac{1}{4} π h^{3} \end{aligned}$ . The mass (in grams) of each sample in terms of height can be modeled by %20%3D%20%5Cfrac%7B1%7D%7B4%7Dh%5E3%20-%20h%5E2%20%2B%205h"> $\begin{aligned} M (h) = \frac{1}{4} h^{3} - h^{2} + 5 h \end{aligned}$ . Write an expression that represents the density of the samples. (Hint: $\begin{aligned} D = \frac{M}{V} \end{aligned}$ )
::一组地质学家从提议的矿址收集了物质样品,必须查明该物质。每个样品大致是圆柱形的。作为圆柱形高度(以厘米计)的函数,每个样品的体积是V=14h3。每个样品的重量(克)可以M=14h3-h2+5h为模型。写一个表示样品密度的表达式。 (Hint:D=MV)

Divide using synthetic division:
::使用合成分数的除法 :

$\begin{aligned} 4 x^{3} - 3 x^{2} + x + 1 \end{aligned}$ divided by $\begin{aligned} (x^{2} - 1) \end{aligned}$
::4x3-3x2+x+1除以(x2-1)

$\begin{aligned} x^{4} - x^{2} + 1 \end{aligned}$ divided by $\begin{aligned} (x^{2} + 1) \end{aligned}$
::x4 - x2+1 除以 (x2+1)

$\begin{aligned} 2 x^{4} - \frac{1}{2} x^{2} + 2 x \end{aligned}$ divided by $\begin{aligned} (4 x^{2} - 1) \end{aligned}$
::2x4 - 12x2+2x除以( 4x2 - 1)

$\begin{aligned} 4 x^{3} - 3 x^{2} + x + 1 \end{aligned}$ divided by $\begin{aligned} (4 x^{2} + 1) \end{aligned}$
::4x3-3x2+x+1除以(4x2+1)

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

多项式的综合除法

Synthetic Division of Polynomials ::多项式的综合除法

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)

Synthetic Division of Polynomials
::多项式的综合除法

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Review
::回顾

Review (Answers)
::回顾(答复)