9.6 数字度和分数度不同时的图形绘制

Section outline

• Select section General

  Collapse Expand

  General

  Collapse all Expand all

  • Select activity 新闻通告

    

    新闻通告 Forum
• Select section 数字和分数度不同时的图形绘制

  Collapse Expand

  数字和分数度不同时的图形绘制

  播放段落

  Xerxes says that the function $\begin{align*}y=\frac{x-2}{4x^2 + 7}\end{align*}$ , has a horizontal asymptote of $\begin{align*}y = \frac{1}{4}\end{align*}$ , Yolanda says the function has no horizontal asymptote, Zeb says that it does have a horizontal asymptote but it's at $\begin{align*}y=0\end{align*}$ . Which one of them is correct?
  ::Xerxes 表示函数 y=x- 24x2+7 具有 Y=14 的水平同位数, Yolanda 表示函数没有水平同位数, Zeb 表示函数确实有水平同位数, 但是在 y=0 。 其中哪一个正确 ?

  播放段落

  Graphing Rational Functions
  ::图形推理函数

  播放段落

  In this concept we will touch on the different possibilities for the remaining types of rational functions . You will need to use your graphing calculator throughout this concept to ensure your sketches are correct.
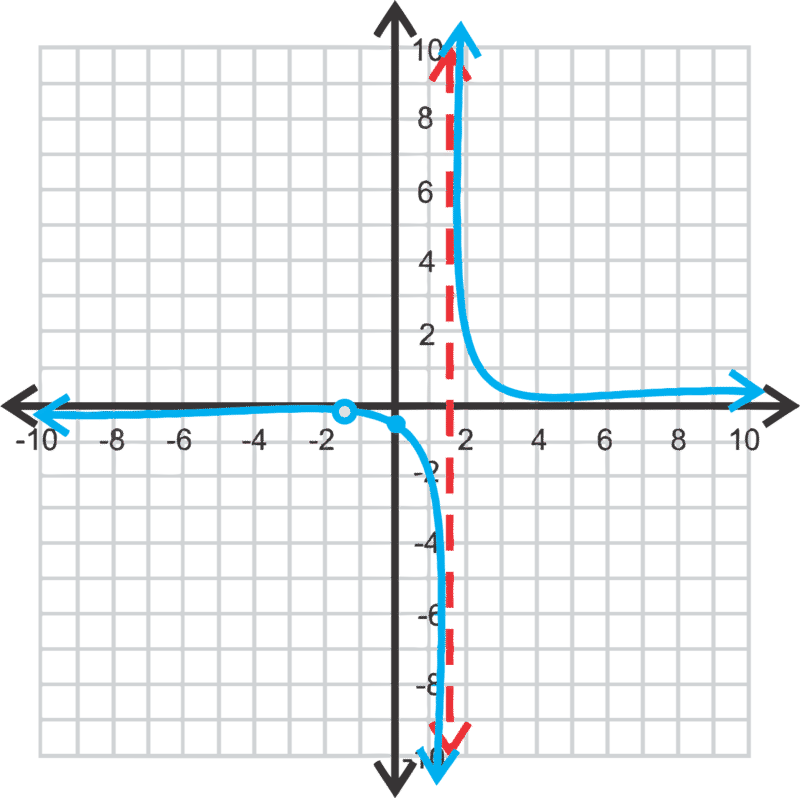
  ::在这个概念中,我们将触及剩余类型的理性函数的不同可能性。 您需要在整个概念中使用您的图形计算器, 以确保您的素描正确无误 。

  播放段落

  Let's graph $\begin{align*}y=\frac{x+3}{2x^2+11x-6}\end{align*}$  and find all asymptotes , intercepts , and the domain and range .
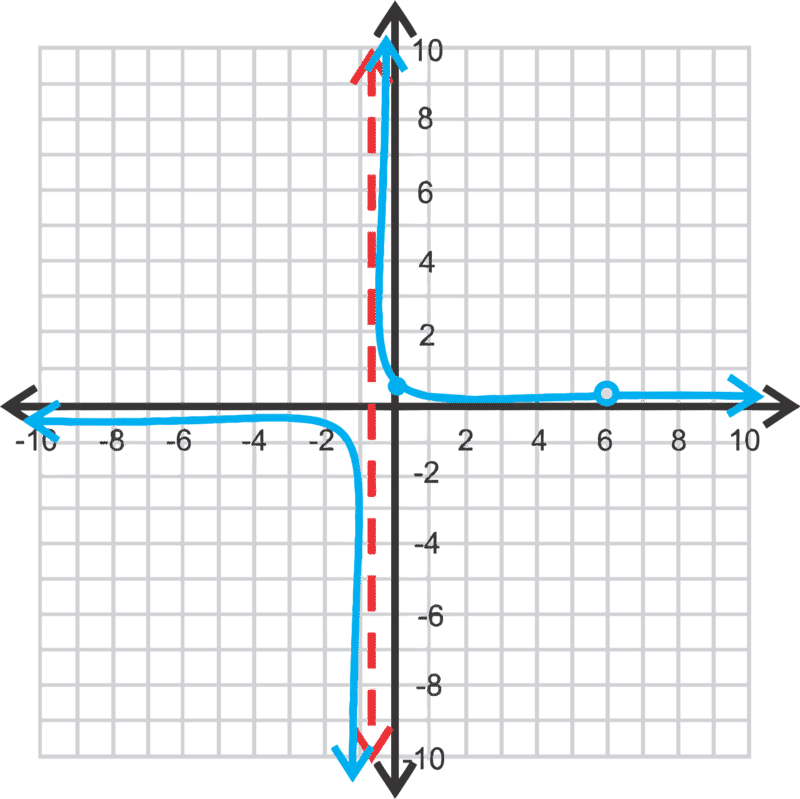
  ::让我们来绘制 y=x+32x2+11x-6, 并查找所有 asymptotes, 拦截, 以及域域和范围 。

  播放段落

  In this problem   the degree of the numerator is less than the degree of the denominator. Whenever this happens the horizontal asymptote will be $\begin{align*}y = 0\end{align*}$ , or the $\begin{align*}x\end{align*}$ -axis. Now, even though the $\begin{align*}x\end{align*}$ -axis is the horizontal asymptote, there will still be a zero at $\begin{align*}x = -3\end{align*}$ (solving the numerator for $\begin{align*}x\end{align*}$ and setting it equal to zero). The vertical asymptotes will be the solutions to $\begin{align*}2x^2+11x-6=0\end{align*}$ . Factoring this quadratic, we have $\begin{align*}(2x-1)(x+6)=0\end{align*}$ and the solutions are $\begin{align*}x=\frac{1}{2}\end{align*}$ and $\begin{align*}-6\end{align*}$ . The $\begin{align*}y\end{align*}$ - intercept is $\begin{align*}\left(0,- \frac{1}{2}\right)\end{align*}$ . At this point, we can plug our function into the graphing calculator to get the general shape.
  ::在此问题上, 分子的程度低于分母的程度 。 每当发生这种情况时, 水平的静态将是 y=0 或 x- 轴 。 现在, 即使 x 轴是 水平的静态, 在 x% 3 时, 仍然会有 0 ( X) 3 点( 解开 x 的分子, 将其设置为为 0) 。 垂直静态将是 2x2+11x-6 =0 的解决方案 。 计算这个二次方形时, 我们有 2x-1 (x+6) =0 , 解决方案是 x=12 和 -6 点 。 y 插口是 ( 0, -12) 。 此时, 我们可以在图形计算器中插入我们的功能, 以获取普通形状 。

  

  播放段落

  Because the middle portion crosses over the horizontal asymptote, the range will be all real numbers. The domain is $\begin{align*}x \in \mathbb{R};x=-6;x \ne \frac{1}{2}\end{align*}$ .
  ::因为中间部分横跨水平等量, 范围将全部为真实数字。 域是 xR; x6; x12 。

  播放段落

  Be careful when graphing any rational function. This function does not look like the graph to the left in a TI-83/84. This is because the calculator does not have the ability to draw the asymptotes separately and wants to make the function continuous . Make sure to double-check the table ( $\begin{align*}2^{\text{nd}} \rightarrow\end{align*}$ GRAPH) to find where the function is undefined .
  ::当绘制任何理性函数时要小心。 此函数看起来不像 TI- 83/84 中左侧的图形。 这是因为计算器没有能力单独绘制小数图, 并且想要使函数连续。 请确保双倍检查表格 (2nd & GRAPH) , 以找到函数未定义的位置 。

  播放段落

  Now, let's graph $\begin{align*}f(x)=\frac{x^2+7x-30}{x+5}\end{align*}$  and find all asymptotes, intercepts, and the domain and range.
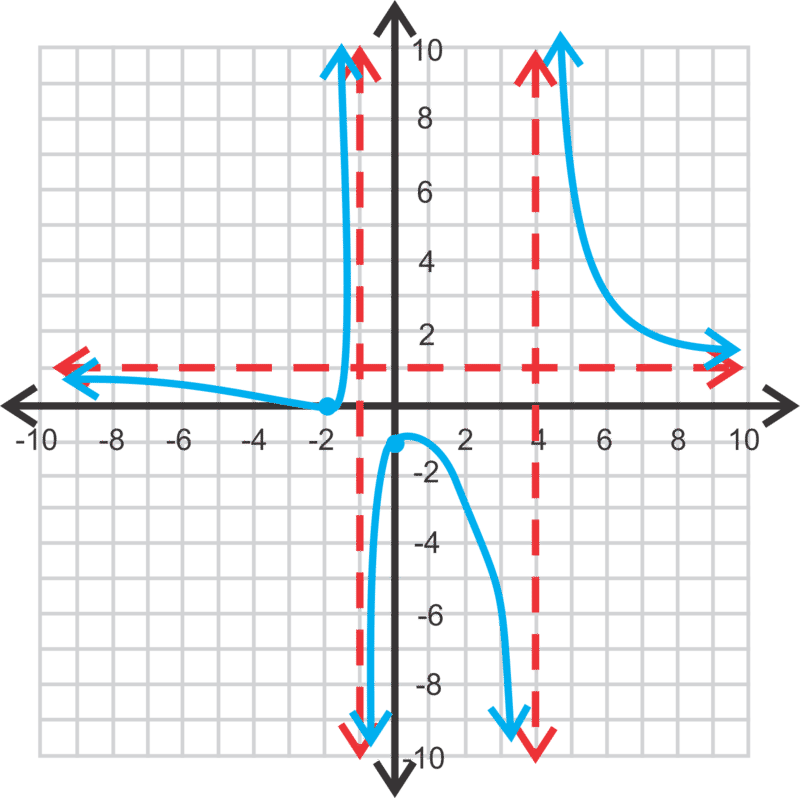
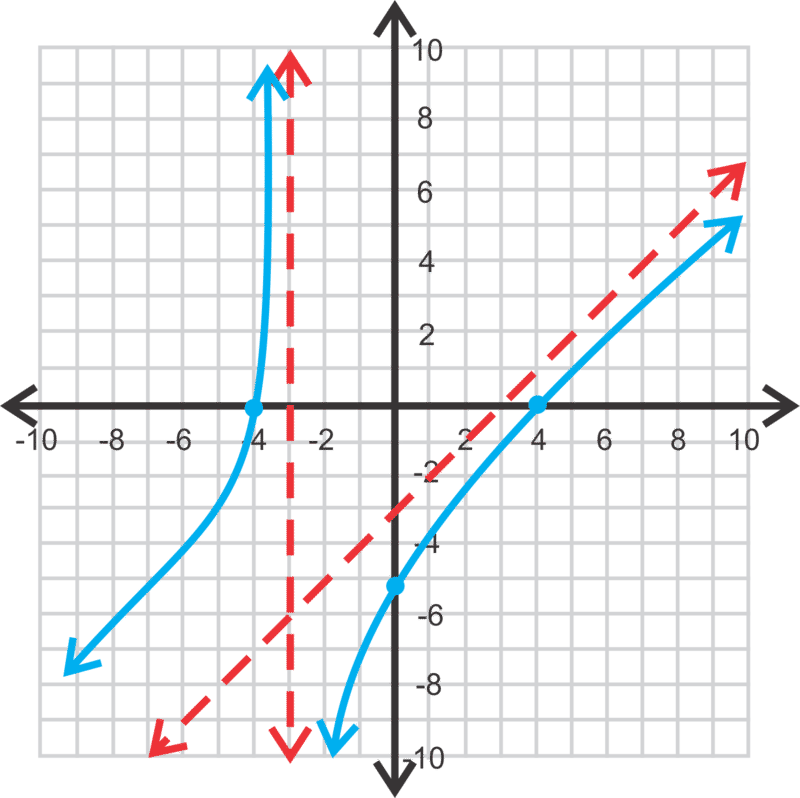
  ::现在,让我们来图f(x) =x2+7x-30x+5, 并查找所有小数点、 拦截、 域域和范围 。

  播放段落

  In this problem   the degree of the numerator is greater than the degree of the denominator . When this happens, there is no horizontal asymptote. Instead there is a slant asymptote . Recall that this function represents division . If we were to divide $\begin{align*}x^2+7x-30\end{align*}$ by $\begin{align*}x+5\end{align*}$ , the answer would be $\begin{align*}x+2-\frac{20}{x+5}\end{align*}$ . The slant asymptote would be the answer, minus the remainder. Therefore ,for this problem the slant asymptote is $\begin{align*}y=x+2\end{align*}$ . Everything else is the same. The $\begin{align*}y\end{align*}$ -intercept is $\begin{align*}\frac{-30}{5} \rightarrow (0,-6)\end{align*}$ and the $\begin{align*}x\end{align*}$ -intercepts are the solutions to the numerator, $\begin{align*}x^2+7x-30=0 \rightarrow (x+10)(x-3) \rightarrow x=-10,3\end{align*}$ . There is a vertical asymptote at $\begin{align*}x = -5\end{align*}$ . At this point, you can either test a few points to see where the branches are or use your graphing calculator.
  ::在此问题上, 分子的度大于分母的分母度。 发生这种情况时, 没有水平的静态。 相反, 存在倾斜的静态。 回顾此函数代表分裂。 如果我们将 x2+7x- 30 除以 x+5, 答案将是 x+2-20x+5 。 那么, 倾斜的静态就是答案, 减去其余部分。 因此, 对于这个问题, 倾斜的静态是 y=x+2 。 其它的一切都是一样的。 y 截取是- 305( 0, - 6 ) , 而 x 截取是算术的解决方案 , x2+7x- 30=0.% ( x+10) (x- 3) {x10 。 。 在 x { 5 点, 您可以测试几个点来查看分支的位置或使用您的图形计算器 。

  

  播放段落

  The domain would be all real numbers; $\begin{align*}x \ne -5\end{align*}$ . Because of the slant asymptote, there are no restrictions on the range. It is all real numbers.
  ::域名将全部为真实数字; x5。 由于倾斜无序, 没有限制范围。 它都是真实数字 。

  播放段落

  Finally, let's graph $\begin{align*}y=\frac{x-6}{3x^2-16x-12}\end{align*}$  and find the asymptotes and intercepts.
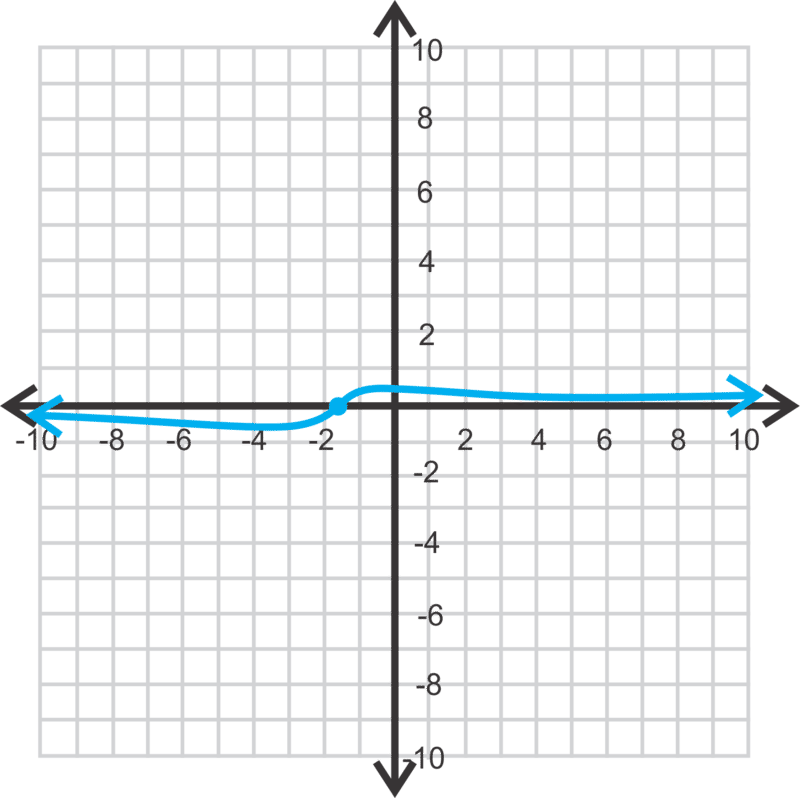
  ::最后,让我们来图y=x-63x2-16x-12 并找到小行星和拦截物。

  播放段落

  Because the degree of the numerator is less than the degree of the denominator, there will be a horizontal asymptote along the $\begin{align*}x\end{align*}$ -axis. Next, let’s find the vertical asymptotes by factoring the denominator; $\begin{align*}(x-6)(3x+2)\end{align*}$ . Notice that the denominator has a factor of $\begin{align*}(x-6)\end{align*}$ , which is the entirety of the numerator. That means there will be a hole at $\begin{align*}x=6\end{align*}$ .
  ::由于分子的分母度小于分母的分母度, x 轴上将有一个水平的同量点。 接下来,让我们通过对分母进行系数化来找到垂直的同量点;( x-6 (3x+2) ) 。 请注意, 分母有一个( x-6 ) 系数, 也就是数子的完整。 这意味着 x=6 上将有一个洞 。

  

  播放段落

  Therefore, the graph of $\begin{align*}y=\frac{x-6}{3x^2-16x-12}\end{align*}$ will be the same as $\begin{align*}y=\frac{1}{3x+2}\end{align*}$ except with a hole at $\begin{align*}x = 6\end{align*}$ . There is no $\begin{align*}x\end{align*}$ -intercept, the vertical asymptote is at $\begin{align*}x=- \frac{2}{3}\end{align*}$ and the $\begin{align*}y\end{align*}$ -intercept is $\begin{align*}\left(0,\frac{1}{2}\right)\end{align*}$ .
  ::因此,y=x-63x2-16x-12的图形将与y=13x+2相同,但X=6的空洞除外。 没有 x intercut, 垂直的空位在 x23, y intercut is (0, 12) 。

  播放段落

  Recap
  ::复述( C)

  播放段落

  For a rational function; $\begin{align*}f(x)=\frac{p\left(x\right)}{q\left(x\right)}=\frac{a_mx^m+ \ldots +a_0}{b_nx^n+ \ldots +b_0}\end{align*}$
  ::合理函数; f( x)=p( x)q( x)=amxm+...+a0bnxn+...+b0

  播放段落
  1. If $\begin{align*}m<n\end{align*}$ , then there is a horizontal asymptote at $\begin{align*}y = 0\end{align*}$ .
     ::如果 m < n, 那么y=0 就会有一个水平同位数 。
  播放段落
  2. If $\begin{align*}m=n\end{align*}$ , then there is a horizontal asymptote at $\begin{align*}y=\frac{a_m}{b_n}\end{align*}$ (ratio of the leading coefficients).
     ::如果 m=n, y= ambn (主要系数的比值) 就会有一个水平的同位数 。
  播放段落
  3. If $\begin{align*}m>n\end{align*}$ , then there is a slant asymptote at $\begin{align*}y=(a_mx^m+\ldots+a_0) \div (b_nx^n+\ldots+b_0)\end{align*}$ without the remainder. In this concept, we will only have functions where $\begin{align*}m\end{align*}$ is one greater than $\begin{align*}n\end{align*}$ .
     ::如果 m>n , 那么y=( amxm+...+a0)\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

  播放段落

  Examples
  ::实例

  播放段落

  Example 1
  ::例1

  播放段落

  Earlier, you were asked to determine which student is correct. 
  ::早些时候,有人要求你确定哪个学生是正确的。

  播放段落

  The degree of the numerator $\begin{align*}x-2\end{align*}$ is less than the degree of the denominator $\begin{align*}4x^2 + 7\end{align*}$ . We know that whenever this happens the horizontal asymptote will be $\begin{align*}y = 0\end{align*}$ , or the $\begin{align*}x\end{align*}$ -axis.
  ::分子x-2的度小于分母 4x2+7 的度。 我们知道,一旦发生这种情况, 水平衰变将是y=0 或 x 轴 。

  播放段落

  Therefore, Zeb is correct.
  ::因此,Zeb是正确的。

  播放段落

  Graph the following functions. Find any intercepts and asymptotes.
  ::图形显示以下函数。查找任何拦截和微粒。

  播放段落

  Example 2
  ::例2

  播放段落

  $\begin{align*}y=\frac{3x+5}{2x^2+9x+20}\end{align*}$
  ::y=3x+52x2+9x+20

  播放段落

  $\begin{align*}x\end{align*}$ -intercept: $\begin{align*}\left(- \frac{5}{3},0\right)\end{align*}$ , $\begin{align*}y\end{align*}$ -intercept: $\begin{align*}\left(0,\frac{1}{4}\right)\end{align*}$
  ::x 拦截-53,0) y 拦截0,14)

  播放段落

  horizontal asymptote: $\begin{align*}y=0\end{align*}$
  ::水平时间: y=0

  播放段落

  vertical asymptotes: none
  ::垂直等模点数: 无

  

  播放段落

  Example 3
  ::例3

  播放段落

  $\begin{align*}f(x)=\frac{x^2+4x+4}{x^2-3x-4}\end{align*}$
  :x) =x2+4x+4x2-3x-4

  播放段落

  $\begin{align*}x\end{align*}$ -intercept: $\begin{align*}(-2,0)\end{align*}$ , $\begin{align*}y\end{align*}$ -intercept: $\begin{align*}(0,-1)\end{align*}$
  ::x 拦截-2,0) y 拦截0,-1)

  播放段落

  horizontal asymptote: $\begin{align*}y=1\end{align*}$
  ::水平时间: y=1

  播放段落

  vertical asymptotes: $\begin{align*}x=4\end{align*}$ and $\begin{align*}x=-1\end{align*}$
  ::垂直单位数 : x=4 和 x1

  

  播放段落

  Example 4
  ::例4

  播放段落

  $\begin{align*}g(x)=\frac{x^2-16}{x+3}\end{align*}$
  ::g(x) =x2 - 16x+3

  播放段落

  $\begin{align*}x\end{align*}$ -intercepts: $\begin{align*}(-4,0)\end{align*}$ and $\begin{align*}(4,0)\end{align*}$
  ::x 拦截-4,0)和(-4,0)

  播放段落

  $\begin{align*}y\end{align*}$ -intercept: $\begin{align*}\left(0,- \frac{16}{3}\right)\end{align*}$
  ::y 拦截: (0, - 163)

  播放段落

  slant asymptote: $\begin{align*}y=x-3\end{align*}$
  ::倾斜渐移: y=x- 3

  播放段落

  vertical asymptotes: $\begin{align*}x=-3\end{align*}$
  ::垂直数位数 : x3

  

  播放段落

  Example 5
  ::例5

  播放段落

  $\begin{align*}y=\frac{2x+3}{6x^2-x-15}\end{align*}$
  ::y= 2x+36x2 - x- 15

  播放段落

  $\begin{align*}x\end{align*}$ -intercepts: none, hole at $\begin{align*}x = - \frac{3}{2}\end{align*}$
  ::x 截取器: 无, x% 32 洞口

  播放段落

  $\begin{align*}y\end{align*}$ -intercept: $\begin{align*}\left(0,- \frac{1}{5}\right)\end{align*}$
  ::y 拦截: (0, - 15)

  播放段落

  horizontal asymptote: $\begin{align*}y=0\end{align*}$
  ::水平时间: y=0

  播放段落

  vertical asymptote: $\begin{align*}x=\frac{5}{3}\end{align*}$
  ::垂直垂直时间数 : x=53

  

  播放段落

  Review
  ::回顾

  播放段落

  Find all asymptotes of the following functions.
  ::查找以下函数的所有微量。

  播放段落
  1. $\begin{align*}y=\frac{x-2}{x^2+6x+8}\end{align*}$
     ::y=x- 2x2+6x+8
  播放段落
  2. $\begin{align*}y=\frac{x^2-4}{x+5}\end{align*}$
     ::y=x2 - 4x+5 y=x2 - 4x+5
  播放段落
  3. $\begin{align*}y=\frac{x^2}{x-3}\end{align*}$
     ::y=x2x- 3 y=x2x- 3
  播放段落
  4. Find the x -intercepts of the function in #2.
     ::在 # 2 中查找函数的 x 界面 。
  播放段落
  5. Find the x -intercepts of the function in #3.
     ::在 # 3 中查找函数的 x 界面 。

  播放段落

  Graph the following functions. Find any intercepts, asymptote and holes.
  ::绘制以下函数的图。 查找任何拦截、 空洞和空洞 。

  播放段落
  6. $\begin{align*}y=\frac{x+1}{x^2-x-12}\end{align*}$
     ::y=x+1x2-x- 12 y=x+1x2-x- 12
  播放段落
  7. $\begin{align*}f(x)=\frac{x^2+3x-10}{x-3}\end{align*}$
     :xx) =x2+3x-10x-3
  播放段落
  8. $\begin{align*}y=\frac{x-7}{2x^2-11x-21}\end{align*}$
     ::y=x - 72x2 - 11x- 21
  播放段落
  9. $\begin{align*}g(x)=\frac{2x^2-2}{3x+5}\end{align*}$
     ::g(x) = 2x2 - 23x+5
  播放段落
  10. $\begin{align*}y=\frac{x^2+x-30}{x+6}\end{align*}$
      ::y=x2+x-30x+6 y=x2+x-30x+6
  播放段落
  11. $\begin{align*}f(x)=\frac{x^2+x-30}{2x^3-5x^2-4x+3}\end{align*}$
      :x) =x2+x- 302x3- 5x2-4x+3
  播放段落
  12. $\begin{align*}y=\frac{x^3-2x^2-3x}{x^2-5x+6}\end{align*}$
      ::y=x3 - 2x2 - 3x2 - 5x+6 y=3 - 2x2 - 3x22 - 5x+6
  播放段落
  13. $\begin{align*}f(x)=\frac{2x+5}{x^2+5x-6}\end{align*}$
      :x)=2x+5x2+5x-6
  播放段落
  14. $\begin{align*}g(x)=\frac{-x^2+3x+4}{2x-6}\end{align*}$
      ::g(x) x2+3x+42x-6
  播放段落
  15. Determine the slant asymptote of $\begin{align*}y=\frac{3x^2-x-10}{3x+5}\end{align*}$ . Now, graph this function. Is there really a slant asymptote? Can you explain your results?
      ::确定 y= 3x2- x- 103x+5 的倾斜渐移。 现在, 请绘制此函数 。 真的存在倾斜渐移吗 ? 您能否解释您的结果 ?

  播放段落

  Review (Answers)
  ::回顾(答复)

  播放段落

  Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
  ::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键 。