Course: 9.15 使用液晶解析法解析理衡

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 使用液晶解析

Collapse Expand
使用液晶解析
A right triangle has leg lengths of $\begin{align*}\frac{1}{2}\end{align*}$ and $\begin{align*}\frac{1}{x}\end{align*}$ units. Its hypotenuse is 2 units. What is the value of x ?
::右三角形的腿长度为 12 和 1x 单位。其下限为 2 个单位。 x 值是多少 ?

Solving Rational Equations
::解决合理等式

In addition to using cross- multiplication to solve a rational equation , we can also use the LCD of all the rational expressions within the equation and eliminate the fraction . To demonstrate, we will walk through a few problems.
::除了使用交叉乘法解决理性方程式之外,我们还可以使用方程式中所有理性表达的液晶,消除分数。为了证明这一点,我们将解决几个问题。

Let's solve the following rational equations.
::让我们解决以下的理性方程式。

$\begin{align*}\frac{5}{2}+\frac{1}{x}=3\end{align*}$
::52+1x=3

The LCD for 2 and $\begin{align*}x\end{align*}$ is $\begin{align*}2x\end{align*}$ . Multiply each term by $\begin{align*}2x\end{align*}$ , so that the denominators are eliminated. We will put the $\begin{align*}2x\end{align*}$ over 1, when multiplying it by the fractions, so that it is easier to line up and cross-cancel.
::2 和 x 的 LCD 是 2x. 乘以 2x 。每个术语乘以 2x , 以便消除分母。当将 2x 乘以 1 乘以分数时, 我们将会将 2x 乘以 1 , 以便更容易排成一行并交叉排出。

$\begin{aligned} \frac{5}{2} + \frac{1}{x} & = 3 \\ \frac{2 x}{1} \cdot \frac{5}{2} + \frac{2 x}{1} \cdot \frac{1}{x} & = 2 x \cdot 3 \\ 5 x + 2 & = 6 x \\ 2 & = x \end{aligned}$
$\begin{align*}\frac{5}{2}+ \frac{1}{x}&=3 \\ {\color{blue}\frac{\cancel{2}x}{1}} \cdot \frac{5}{\cancel{2}}+ {\color{blue}\frac{2\cancel{x}}{1}} \cdot \frac{1}{\cancel{x}}&=2x \cdot 3 \\ 5x+2&=6x \\ 2&=x\end{align*}$
::52+1x=32x1=52x1=2x1=1x1x1x=2x_35x+2=6x2=x

Checking the answer, we have $\begin{align*}\frac{5}{2}+ \frac{1}{2}=3 \rightarrow \frac{6}{2}=3 \end{align*}$
::正在检查答案, 我们有52+12=362=3

$\begin{align*}\frac{5x}{x-2}=7+ \frac{10}{x-2}\end{align*}$
::5xx-2=7+10x-2

Because the denominators are the same, we need to multiply all three terms by $\begin{align*}x-2\end{align*}$ .
::因为分母是相同的, 我们需要将所有三个条件乘以 x-2 。

$\begin{aligned} \frac{5 x}{x - 2} & = 7 + \frac{10}{x - 2} \\ (x - 2) \cdot \frac{5 x}{x - 2} & = (x - 2) \cdot 7 + (x - 2) \cdot \frac{10}{x - 2} \\ 5 x & = 7 x - 14 + 10 \\ - 2 x & = - 4 \\ x & = 2 \end{aligned}$
$\begin{align*}\frac{5x}{x-2}&=7+ \frac{10}{x-2} \\ {\color{blue}\cancel{(x-2)}} \cdot \frac{5x}{\cancel{x-2}}&={\color{blue}(x-2)} \cdot 7+{\color{blue}\cancel{(x-2)}} \cdot \frac{10}{\cancel{x-2}} \\ 5x&=7x-14+10 \\ -2x&=-4 \\ x&=2\end{align*}$
::5x-2=7+10x-2(x-2)5x-2(2x-2)5x-2=(x-2)7+(x-2)2,(x-2)10x-25x=7x-14+10-2xx*4x=2

Checking our answer, we have: $\begin{align*}\frac{5 \cdot 2}{2-2}=7+ \frac{10}{2-2} \rightarrow \frac{10}{0}=7+\frac{10}{0}\end{align*}$ . Because the solution is the vertical asymptote of two of the expressions, $\begin{align*}x=2\end{align*}$ is an extraneous solution . Therefore , there is no solution to this problem.
::正在检查我们的答案, 我们有: 522-2=7+102-2100=7+100。因为解决方案是两个表达式的垂直零点, x=2 是一个不相干的解决办法。因此, 这个问题没有解决办法。

$\begin{align*}\frac{3}{x}+\frac{4}{5}=\frac{6}{x-2}\end{align*}$
::3x+45=6x-2

Determine the LCD for 5, $\begin{align*}x\end{align*}$ , and $\begin{align*}x-2\end{align*}$ . It would be the three numbers multiplied together: $\begin{align*}5x(x-2)\end{align*}$ . Multiply each term by the LCD.
::确定 5, x 和 x-2 的 LCD 。 3 个数字乘以: 5x(x-2), 乘以 5x(x-2) 。

$\begin{aligned} \frac{3}{x} + \frac{4}{5} & = \frac{6}{x - 2} \\ \frac{5 x (x - 2)}{1} \cdot \frac{3}{x} + \frac{5 x (x - 2)}{1} \cdot \frac{4}{5} & = \frac{5 x (x - 2)}{1} \cdot \frac{6}{x - 2} \\ 15 (x - 2) + 4 x (x - 2) & = 30 x \end{aligned}$
$\begin{align*}\frac{3}{x}+ \frac{4}{5}&=\frac{6}{x-2} \\ {\color{blue}\frac{5 \cancel{x} \left(x-2\right)}{1}} \cdot \frac{3}{\cancel{x}}+ {\color{blue}\frac{\cancel{5}x \left(x-2\right)}{1}} \cdot \frac{4}{\cancel{5}}&={\color{blue}\frac{5x \cancel{\left(x-2\right)}}{1}} \cdot \frac{6}{\cancel{x-2}} \\ 15(x-2)+4x(x-2)&=30x\end{align*}$
::3x+45=6x-25x(x-2)13x+5x(x-2)145=5x(x-2)16x-215(x-2)+4x(x-2)=30x

Multiplying each term by the entire LCD cancels out each denominator, so that we have an equation that we have learned how to solve in previous concepts. Distribute the 15 and $\begin{align*}4x\end{align*}$ , combine like terms and solve.
::将每个术语乘以整个 LCD 取消每个分母, 这样我们就能有一个在先前的概念中学会了如何解答的等式。分配 15 和 4x, 将词词和解题结合起来。

$\begin{aligned} 15 x - 30 + 4 x^{2} - 8 x & = 30 x \\ 4 x^{2} - 23 x - 30 & = 0 \end{aligned}$
$\begin{align*}15x-30+4x^2-8x&=30x \\ 4x^2-23x-30&=0\end{align*}$
::15 - 30+4x2 - 8x=30x4x2 - 23x - 30=0

This polynomial is not factorable. Let’s use the Quadratic Formula to find the solutions.
::这个多元性是不可考虑的。让我们使用二次曲线公式来找到解决方案。

$\begin{align*}x=\frac{23 \pm \sqrt{\left(-23\right)^2-4 \cdot 4 \cdot \left(-30\right)}}{2 \cdot 4}=\frac{23 \pm \sqrt{1009}}{8}\end{align*}$
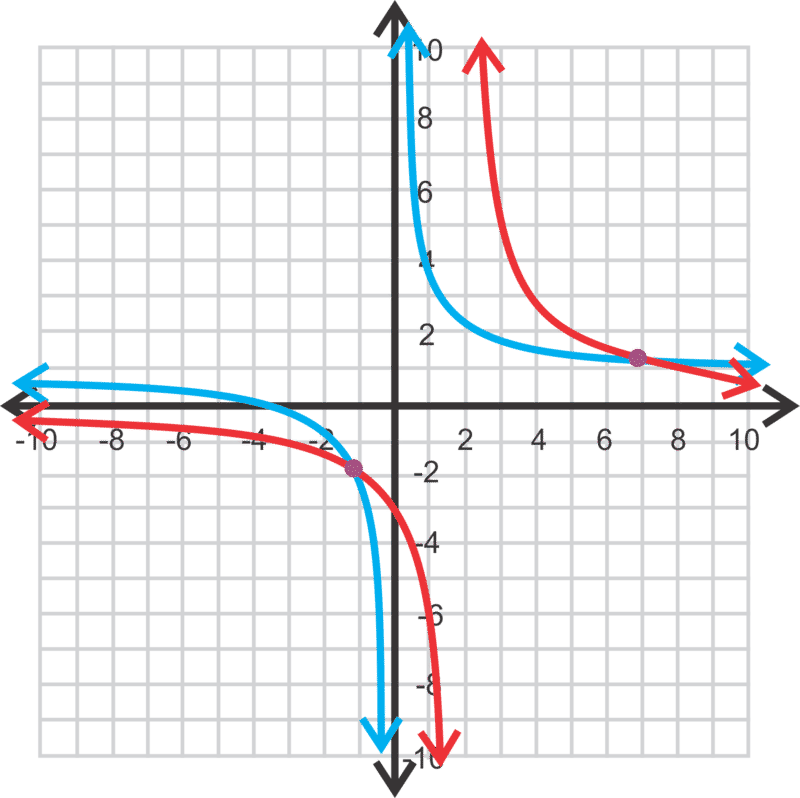
::x=23(-23)2-44(-30)24=2310098

Approximately, the solutions are $\begin{align*}\frac{23+ \sqrt{1009}}{8}\approx 6.85\end{align*}$ and $\begin{align*}\frac{23- \sqrt{1009}}{8}\approx -1.096\end{align*}$ . It is harder to check these solutions. The easiest thing to do is to graph $\begin{align*}\frac{3}{x}+ \frac{4}{5}\end{align*}$ in $\begin{align*}Y1\end{align*}$ and $\begin{align*}\frac{6}{x-2}\end{align*}$ in $\begin{align*}Y2\end{align*}$ (using your graphing calculator).
::大致而言,解决方案为 23+100986.85 和 23- 100981.096。比较难检查这些解决方案。最容易做的是 Y1 中的图3x+45 和 Y2 中的图6x-2( 使用您的图形计算器)。

The $\begin{align*}x\end{align*}$ -values of the points of intersection (purple points in the graph) are approximately the same as the solutions we found.
::交叉点的 x 值( 图形中的纯点) 与我们找到的解决方案大致相同。

Examples
::实例

Example 1
::例1

Earlier, you were asked to find the value of x.
::早些时候,你被要求找到x的值。

We need to use the Pythagorean Theorem to solve for x .
::我们需要用毕达哥伦理论解答x

$\begin{aligned} (\frac{1}{2})^{2} + (\frac{1}{x})^{2} = 2^{2} \\ \frac{1}{4} + \frac{1}{x^{2}} = 4 \\ \frac{4 x^{2}}{1} \cdot \frac{1}{4} + \frac{4 x^{2}}{1} \cdot \frac{1}{x^{2}} & = 4 \cdot 4 x^{2} \\ x^{2} + 4 & = 16 x^{2} \\ 4 = 15 x^{2} \\ \frac{4}{15} = x^{2} \\ x = \frac{2 \sqrt{15}}{15} \end{aligned}$
$\begin{align*}(\frac{1}{2})^2 +(\frac{1}{x})^2 = 2^2\\ \frac{1}{4} + \frac{1}{x^2} = 4\\ {\color{blue}\frac{\cancel{4}x^2}{1}} \cdot \frac{1}{\cancel{4}}+ {\color{blue}\frac{4\cancel{x^2}}{1}} \cdot \frac{1}{\cancel{x^2}}&=4 \cdot 4x^2 \\ x^2+4&=16x^2 \\ 4=15x^2\\ \frac{4}{15}=x^2\\ x=\frac{2\sqrt{15}}{15}\end{align*}$
:12)2+(1x)2=2214+1x2=44x21}14+4x21_1x2=44x2x2+4x24=15x2415=x2x=215)

Solve the following equations.
::解决以下方程式。

Example 2
::例2

$\begin{align*}\frac{2x}{x-3}=2+\frac{3x}{x^2-9}\end{align*}$
::2xx-3=2+3xx2-9

The LCD is $\begin{align*}x^2-9\end{align*}$ . Multiply each term by its factored form to cross-cancel.
::液晶显示器为x2-9. 以其因子形式将每个术语乘以横轴。

$\begin{aligned} \frac{2 x}{x - 3} & = 2 + \frac{3 x}{x^{2} - 9} \\ \frac{(x - 3) (x + 3)}{1} \cdot \frac{2 x}{x - 3} & = (x - 3) (x + 3) \cdot 2 + \frac{(x - 3) (x + 3)}{1} \cdot \frac{3 x}{x^{2} - 9} \\ 2 x (x + 3) & = 2 (x^{2} - 9) + 3 x \\ 2 x^{2} + 6 x & = 2 x^{2} - 18 + 3 x \\ 3 x & = - 18 \\ x & = - 6 \end{aligned}$
$\begin{align*}\frac{2x}{x-3}&=2+ \frac{3x}{x^2-9} \\ {\color{blue}\frac{\cancel{\left(x-3\right)}\left(x+3\right)}{1}} \cdot \frac{2x}{\cancel{x-3}}&={\color{blue}(x-3)(x+3) \cdot} 2+ {\color{blue}\frac{\cancel{\left(x-3\right)\left(x+3\right)}}{1}\cdot} \frac{3x}{\cancel{x^2-9}} \\ 2x(x+3)&=2(x^2-9)+3x \\ 2x^2+6x&=2x^2-18+3x \\ 3x&=-18 \\ x&=-6\end{align*}$
::2xx-3=2+3x2-9(x-3)(x+3)1x2x-3=3=(x-3(x+3)(x+3))2+(x-3)(x-3)(x+3)2+(x-3)(x+3)1x3x2-92x(x+3)=2(x2-9)+3x2x2x2+6x2x2-18+3x3xx___18x______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Checking our answer, we have: $\begin{align*}\frac{2 \left(-6\right)}{-6-3}=2+ \frac{3 \left(-6\right)}{\left(-6\right)^2-9} \rightarrow \frac{-12}{-9}=2+ \frac{-18}{27} \rightarrow \frac{4}{3}=2- \frac{2}{3} \end{align*}$
::检查我们的答案,我们有:2(-6)-6-3=2+3(-6)(-6)(-6)2-9*12-9=21827}43=2-23。

Example 3
::例3

$\begin{align*}\frac{4}{x-3}+5=\frac{9}{x+2}\end{align*}$
::4x-3+5=9x+2

The LCD is $\begin{align*}(x-3)(x+2)\end{align*}$ . Multiply each term by the LCD.
::LCD是(x-3)(x+2)。用LCD乘以每个术语。

$\begin{aligned} \frac{4}{x - 3} + 5 & = \frac{9}{x + 2} \\ (x - 3) (x + 2) \cdot \frac{4}{x - 3} + (x - 3) (x + 2) \cdot 5 & = (x - 3) (x + 2) \cdot \frac{9}{x + 2} \\ 4 (x + 2) + 5 (x - 3) (x + 2) & = 9 (x - 3) \\ 4 x + 8 + 5 x^{2} - 5 x - 30 & = 9 x - 27 \\ 5 x^{2} - 10 x + 5 & = 0 \\ 5 (x^{2} - 2 x + 1) & = 0 \end{aligned}$
$\begin{align*}\frac{4}{x-3}+5&=\frac{9}{x+2} \\ {\color{blue}\cancel{(x-3)}(x+2)} \cdot \frac{4}{\cancel{x-3}}+ {\color{blue}(x-3)(x+2)} \cdot 5&={\color{blue}(x-3)\cancel{(x+2)}} \cdot \frac{9}{\cancel{x+2}} \\ 4(x+2)+5(x-3)(x+2)&=9(x-3) \\ 4x+8+5x^2-5x-30&=9x-27 \\ 5x^2-10x+5&=0 \\ 5(x^2-2x+1)&=0 \\\end{align*}$
::4-3+5=9x2x2x-2x-3(x+2x-3)(x+2)4x-3+3+3(x-3)(x+2)5=(x-3(x+2)2)9x24(x+2)+5(x-3(x+2)+2)+5(x-3(x+2)+2)=9(x-34x8+5x5x2-5x2-5x5x-3x9x-275x2-10x5=05(x2x+1)=0

This polynomial factors to be $\begin{align*}5(x-1)(x-1)=0\end{align*}$ , so $\begin{align*}x = 1\end{align*}$ is a repeated solution. Checking our answer, we have $\begin{align*}\frac{4}{1-3}+5=\frac{9}{1+2} \rightarrow -2+5=3 \end{align*}$
::5( x-1)( x-1) (x- 1) =0, 所以 x=1 是一个重复的解决方案。检查我们的答案, 我们有 41- 3+5=91+2 @ 2+5=3

Example 4
::例4

$\begin{align*}\frac{3}{x^2+4x+4}+ \frac{1}{x+2}=\frac{2}{x^2-4}\end{align*}$
::3x2+4x+4+4+1x+2=2x2-2-4

The LCD is $\begin{align*}(x+2)(x+2)(x-2)\end{align*}$ .
::液晶显示器为(x+2)(x+2)(x+2)(x-2)。

$\begin{aligned} \frac{3}{x^{2} + 4 x + 4} + \frac{1}{x + 2} & = \frac{2}{x^{2} - 4} \\ (x + 2) (x + 2) (x - 2) \cdot \frac{3}{(x + 2) (x + 2)} + (x + 2) (x + 2) (x - 2) \cdot \frac{1}{x + 2} & = (x + 2) (x + 2) (x - 2) \cdot \frac{2}{(x - 2) (x + 2)} \\ 3 (x - 2) + (x - 2) (x + 2) & = 2 (x + 2) \\ 3 x - 6 + x^{2} - 4 & = 2 x + 4 \\ x^{2} + x - 14 & = 0 \end{aligned}$
$\begin{align*}\frac{3}{x^2+4x+4}+ \frac{1}{x+2}&=\frac{2}{x^2-4} \\ {\color{blue}\cancel{(x+2)(x+2)}(x-2)} \cdot \frac{3}{\cancel{\left(x+2\right)\left(x+2\right)}}+ {\color{blue}\cancel{(x+2)}(x+2)(x-2)} \cdot \frac{1}{\cancel{x+2}}&={\color{blue}(x+2)\cancel{(x+2)(x-2)}} \cdot \frac{2}{\cancel{\left(x-2\right)\left(x+2\right)}} \\ 3(x-2)+(x-2)(x+2)&=2(x+2) \\ 3x-6+x^2-4&=2x+4 \\ x^2+x-14&=0\end{align*}$
::3x2+4x+4+4+4+4+1x+2+2=2x2x2-2(x+2)(x-2)(x-2)(x+2)(x+2)(x+2)(x+2)(x+2)(x-2)(x+2)(x+2)(x-2)(x-2)(x-2)(x-2)(x-2)(x-2)(x-2)(x-2)(x-2)(x-2)(x-2)(x-2)(x+2)(x)(x2)(x+2)(x+2)(x+2)(x+2)(x+2(x)(x-2)(x-2)(x-2)(x-2)(x+2)(x+2)(x-2)(x+2)(x-2)(x+2)(x-2)(x-2)(x-2)(x-2)(x-2)(x-2)(x-2)(x-2)(x+2)(x-2)(x+2)(x+2)(x-2)(x+2)(x+2)(x+2)(x-2)(x+2)(x+2)(x)3x-2)(x+2)(x+2)(x+2)(x-2)(x+2)(x-2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x)3+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x+2)(x)3)(x)3)(x+2)3x+2)(x+2)(x+2)3)(3)3)(3x+2)(3)(3)(3)(3)(x)3x)3x)(3x-2)(3)(3x-2)(3x)3x-2)(3x-2)(3x-2)(3)(x-2)(2)3)(3)(3)(3)(3)(3)(3)(3x-2)(3)(3)(3)(3)(3)(3)(3)(2)(2)(2)(2)(2)(2)(2)(2)(2)(x-2)(2)(2)(2)(2)(2)(x

This quadratic is not factorable, so we need to use the Quadratic Formula to solve for $\begin{align*}x\end{align*}$ .
::此二次方位是不可因数的, 所以我们需要使用二次方位公式来解析 x 。

$\begin{align*}x=\frac{-1 \pm \sqrt{1-4 \left(-14\right)}}{2}=\frac{-1 \pm \sqrt{57}}{2} \approx 3.27\end{align*}$ and $\begin{align*}-4.27\end{align*}$
::x11-4(-)14215723.27和-4.27

Using your graphing calculator, you can check the answer. The $\begin{align*}x\end{align*}$ -values of points of intersection of $\begin{align*}y=\frac{3}{x^2+4x+4}+ \frac{1}{x+2}\end{align*}$ and $\begin{align*}y=\frac{2}{x^2-4}\end{align*}$ are the same as the values above.
::使用您的图形计算计算器,您可以检查答案。y=3x2+4x+4+4+4+1x+2和y=2x2-4的交叉点的x值与上述值相同。

Review
::回顾

Determine if the following values for x are solutions for the given equations.
::确定 x 的以下值是否为给定方程式的解决方案。

$\begin{align*}\frac{4}{x-3} + 2 = \frac{3}{x+4}, \ x=-1\end{align*}$
::4 - 3+2=3x+4, x1

$\begin{align*}\frac{2x-1}{x-5} - 3 = \frac{x+6}{2x}, \ x=6\end{align*}$
::2 - 1x - 5 - 3=x+62x, x=6

What is the LCD for each set of numbers?
::每组数字的LCD是什么?

$\begin{align*}4-x, \ x^2 - 16\end{align*}$
::4-x, x2-16

$\begin{align*}2x, \ 6x-12, \ x^2 - 9\end{align*}$
::2x, 6x- 12, x2- 9

$\begin{align*}x-3, \ x^2-x-6, \ x^2-4\end{align*}$
::x-3, x2-x-6, x2-4

Solve the following equations.
::解决以下方程式。

$\begin{align*}\frac{6}{x+2}+1=\frac{5}{x}\end{align*}$
::6x+2+1=5x

$\begin{align*}\frac{5}{3x}- \frac{2}{x+1}=\frac{4}{x}\end{align*}$
::53x-2x+1=4x

$\begin{align*}\frac{12}{x^2-9}=\frac{8x}{x-3}- \frac{2}{x+3}\end{align*}$
::12x2-9=8xx-3-2x+3

$\begin{align*}\frac{6x}{x^2-1}+ \frac{2}{x+1}=\frac{3x}{x-1}\end{align*}$
::6x2-1+2x+1=3xx-1

$\begin{align*}\frac{5x-3}{4x}- \frac{x+1}{x+2}=\frac{1}{x^2+2x}\end{align*}$
::5x-34x-x+1x+2=1x2+2x

$\begin{align*}\frac{4x}{x^2+6x+9}- \frac{2}{x+3}=\frac{3}{x^2-9}\end{align*}$
::4x22+6x+9-2x+3=3x2-9

$\begin{align*}\frac{x^2}{x^2-8x+16}=\frac{x}{x-4}+\frac{3x}{x^2-16}\end{align*}$
::x2x2 - 8x+16=xx-4+3x2 - 16

$\begin{align*}\frac{5x}{2x-3}+ \frac{x+1}{x}=\frac{6x^2+x+12}{2x^2-3x}\end{align*}$
::5x2x-3+x+1x=6x2+x+122x2-3x

$\begin{align*}\frac{3x}{x^2+2x-8}=\frac{x+1}{x^2+4x}+\frac{2x+1}{x^2-2x}\end{align*}$
::3xx2+2x-8=x+1x2+4x+2x+2x+1x2-2x

$\begin{align*}\frac{x+1}{x^2+7x}+\frac{x+2}{x^2-3x}=\frac{x}{x^2+4x-21}\end{align*}$
::x+1x2+7x+x2x2x2-3x=x2+4x-21

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

使用液晶解析

Solving Rational Equations ::解决合理等式

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Review ::回顾

Review (Answers) ::回顾(答复)

Solving Rational Equations
::解决合理等式

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Review
::回顾

Review (Answers)
::回顾(答复)