Course: 3.2 一对一的职能及其逆数

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum
Select section 一对一函数及其逆函数

Collapse Expand
一对一函数及其逆函数
The statement "Pizza restaurants sell pizza" could be thought of as a function. It could be plotted on a graph, with different restaurants across the x -axis, and different foods the restaurant specializes in on the y -axis. Any time a pizza restaurant was input into the function, it would output "pizza" as the specialized food.
::“皮萨餐厅销售比萨”的说法可以被视为一种功能。它可以在一张图上绘制,在x轴上各处有不同的餐馆,餐厅有不同的食品专门用于Y轴上。每当一家比萨餐厅投入到这个功能中,它就会将“皮萨”变成专门食品。

Is this pizza restaurant function a one-to-one function? How can we tell?
::这家比萨餐厅是一对一的功能吗?

One-to-One Functions and Their Inverses
::一对一函数及其逆函数

Consider the function $\begin{aligned} f (x) = x^{3} \end{aligned}$ , and its inverse $\begin{aligned} f^{- 1} (x) = \sqrt[3]{x} \end{aligned}$ .
::考虑函数 f( x) =x3 及其反向 f- 1( x) =x3 。

The graphs of these functions are shown below:
::这些功能的图表如下:

The function f ( x ) = x ³ is an example of a one-to-one function, which is defined as follows:
::F(x) 函数 = x3 是一对一函数的示例, 定义如下:

A function is one-to-one if and only if every element of its range corresponds to at most one element of its domain .
::函数为一对一,且只有当其范围的每一要素最多与其域内的一个要素相对应时,才为一对一。

The function y = x ² , however, is not one-to-one. The graph of this function is shown below.
::y = x2 函数不是一对一。此函数的图示如下。

You may recall that you can identify a relation as a function if you can draw a vertical line anywhere through the graph, and the line touches only one point.
::您可能记得,如果您可以通过图形绘制任何一条垂直线,而该线只触及一个点,您就可以将关系确定为函数。

Notice then that if we draw a horizontal line through y = x ² , the line touches more than one point. That indicates that the inverse will not be a function, here is why: If we invert the function y = x ² , the result is a graph that is a reflection over the line y = x , effectively rotating the original 90 degrees. Since x and y have swapped, the new function fails the vertical line test.
::然后请注意,如果我们通过 y = x2 绘制水平线, 线会碰到不止一个点。这表明反向不会是一个函数, 这就是为什么 : 如果我们将函数 y = x2 反转, 结果是一个映射在 y = x 的图形, 有效旋转原90 度。由于 x 和 y 已经交换, 新函数将失败垂直线测试。

The function y = x ² is therefore not a one-to-one function. A function that is one-to-one will be invertible.
::因此,函数 y = x2 不是一对一的函数。一对一的函数是不可倒置的。

You can determine an invertible function graphically by drawing a horizontal line through the graph of the function, if it touches more than one point, the function is not invertible.
::您可以通过在函数的图形中绘制水平线来用图形方式确定一个不可逆函数,如果它触及不止一个点,则该函数是不可逆的。

Examples
::实例

Example 1
::例1

Earlier, you were given a question about a pizza function.
::早些时候,你被问起披萨的功能。

"Pizza restaurants sell pizza" is a function. However, it is NOT a one-to-one function.
::"皮萨餐厅卖披萨"是一种功能,但并不是一对一的功能。

In order to be one-to-one, it must be invertible, giving something like: "pizza sellers are pizza restaurants", and that statement must also be a function.
::为了做到一对一, 它必须是不可逆的, 给类似的东西:“披萨卖家是披萨餐厅”, 而这个声明也必须是一个功能。

Since grocery stores sell pizza, and would therefore be among the outputs of the new function, but were not among the inputs of the original (which specified "pizza restaurants"), the functions are not invertible.
::由于杂货店出售比萨饼,因此将成为新功能的产出之一,但不属于原功能(指定为“披萨餐厅”)的投入,因此这些功能是不可忽略的。

Example 2
::例2

Graph the function $\begin{aligned} f (x) = \frac{1}{3} x + 2 \end{aligned}$ . Use a horizontal line test to verify that the function is invertible.
::绘制函数 f( x) =13x+2. 使用水平线测试来验证函数是不可垂直的。

The graph below shows that this function is invertible. We can draw a horizontal line at any y value, and the line will only cross $\begin{aligned} f (x) = \frac{1}{3} x + 2 \end{aligned}$ once.
::下图显示此函数是不可翻转的。我们可以以任何 y 值绘制水平线, 而该线只横过 f( x) = 13x+2 一次。

In sum, a one-to-one function is invertible. That is, if we invert a one-to-one function, its inverse is also a function. Now that we have established what it means for a function to be invertible, we will focus on the of .
::总而言之,一对一的函数是不可倒置的。也就是说,如果我们将一对一的函数倒置,则其反向也是一种函数。既然我们已经确定了函数不可倒置的含义,我们将集中关注。

Example 3
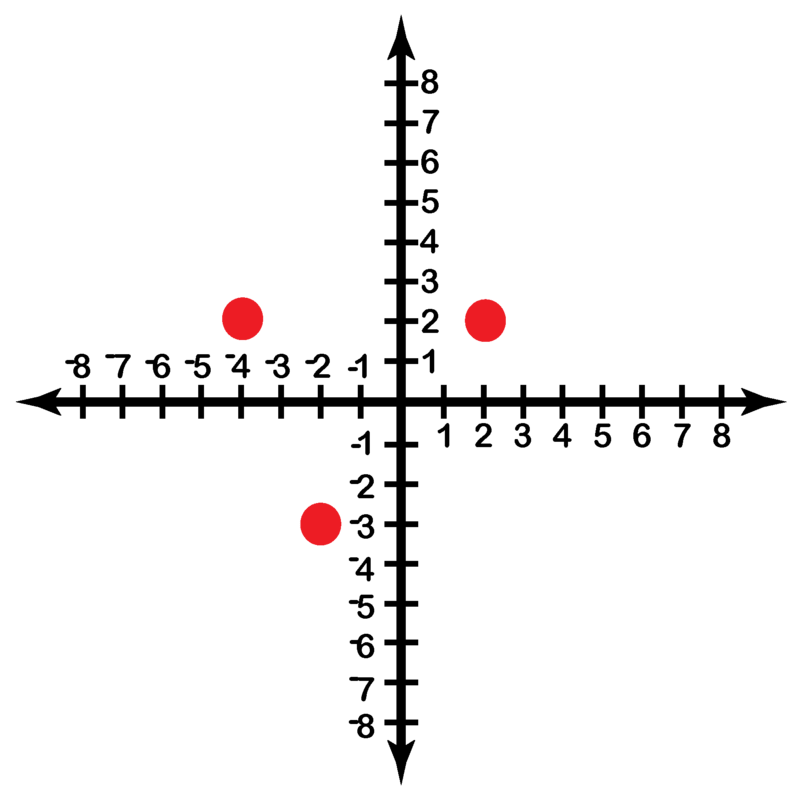
::例3

State the domain and range of the following function and its inverse: (1, 2), (2, 5), (3, 7).
::说明下列函数的域和范围及其反向1、2、2、2、5)、3、7。

The inverse of this function is the set of points (2, 1), (5, 2), (7, 3).
::这一职能的反面是一组点(2、1)、5、2、7、3)。

The domain of the function is {1, 2, 3} . This is also the range of the inverse.
::函数的域为 {1, 2, 3}。这也是反向的范围。

The range of the function is {2, 5, 7} . This is also the domain of the inverse.
::函数的范围为 {2, 5, 7}。这也是反向的域。

The linear functions we examined previously, as well as f ( x ) = x ³ , all had domain and range both equal to the set of all real numbers. Therefore the inverses also had domain and range equal to the set of all real numbers. Because the domain and range were the same for these functions, switching them maintained that relationship.
::我们以前检查过的线性函数,以及 f(x) = x3, 都拥有域和范围, 与所有实际数字的一组相等。因此, 反向也拥有域和范围, 与所有实际数字的一组相等。由于域和范围与这些函数相同, 因此转换它们保持了此关系。

Also, as we found above, the function y = x ² is not one-to-one, and hence it is not invertible. That is, if we invert it, the resulting relation is not a function. We can change this situation if we define the domain of the function in a more limited way. Let f ( x ) be a function defined as follows: f ( x ) = x ² , with domain limited to real numbers ≥ 0. Then the inverse of the function is the square root function: $\begin{aligned} f^{- 1} (x) = \sqrt{x} \end{aligned}$ .
::此外,正如我们上文所发现的那样,函数 y = x2 不是一对一, 因此它不是不可倒置的。也就是说, 如果我们颠倒它, 由此产生的关系不是函数。如果我们以更有限的方式定义函数的域, 我们可以改变这种情况。让 f(x) 成为定义如下的函数 : f(x) = x2, 域限为 = 0。然后函数的反面是平方根函数 : f-1(x) =x。

Example 4
::例4

Define the domain for the function f ( x ) = ( x - 2) ² so that f is invertible.
::定义函数 f(x) = (x - 2) 的域, 使 f 不可对白。

The graph of this function is a parabola . We need to limit the domain to one side of the parabola. Conventionally in cases like these we choose the positive side; therefore, the domain is limited to real numbers ≥ 2.
::此函数的图形是一个抛物线。我们需要将域限制在抛物线的一面。在类似情况中, 通常我们选择积极的一面; 因此, 域限为真数 2 。

Example 5
::例5

Is $\begin{aligned} g (x) = 3 x - 2 \end{aligned}$ a one-to-one function?
::g(x)=3x-2 是一对一函数吗?

Algebraic test for one-to-one functions: if f ( a ) = f ( b ) implies that a = b , then f is one-to-one.
::一对一函数的代数测试:如果f(a)=f(b)意味着a=b,那么f为一对一。

$\begin{aligned} ∴ \end{aligned}$ if $\begin{aligned} g (x) = 3 x - 2 \end{aligned}$ is one-to-one, then $\begin{aligned} g (a) = g (b) \to a = b \end{aligned}$
::如果 g( x) =3x-2 是一对一, 那么 g( a) =g( b) a=b

Test: $\begin{aligned} g (a) = g (b) \end{aligned}$
::测试: g(a)=g(b)

$\begin{aligned} 3 a - 2 = 3 b - 2 \end{aligned}$
::3a-2=3b-2

$\begin{aligned} 3 a = 3 b \end{aligned}$
::3a=3b

$\begin{aligned} a = b \end{aligned}$
::a=b =b

$\begin{aligned} ∴ 3 x - 2 \end{aligned}$ is one-to-one.
::3x-2是一对一

Example 6
::例6

Use the horizontal line test to see if $\begin{aligned} f (x) = x^{3} \end{aligned}$ is one-to-one.
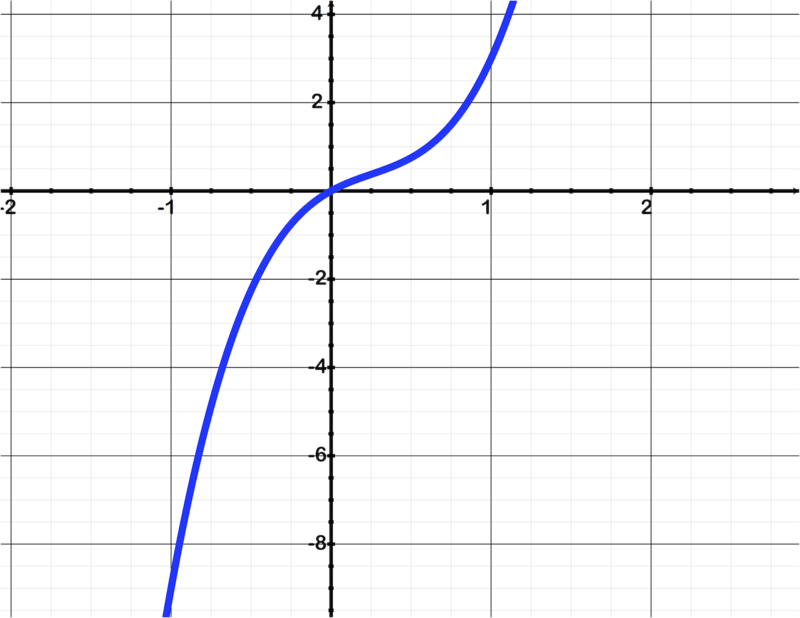
::使用水平线测试查看 f( x) =x3 是一对一。

Graph the equation:
::方程式图解 :

This is the parent function of the cubic function family. Each x value has one unique y-value that is not used by any other x-element. Since that is the definition of a one-to-one function, this function is one-to-one.
::这是立方函数家族的父函数。每个 x 值有一个独特的 Y 值, 而其他任何 x 元素都没有使用。由于这是一对一函数的定义, 此函数为一对一函数。

Example 7
::例7

Is $\begin{aligned} g (x) = | x - 2 | \end{aligned}$ one-to-one?
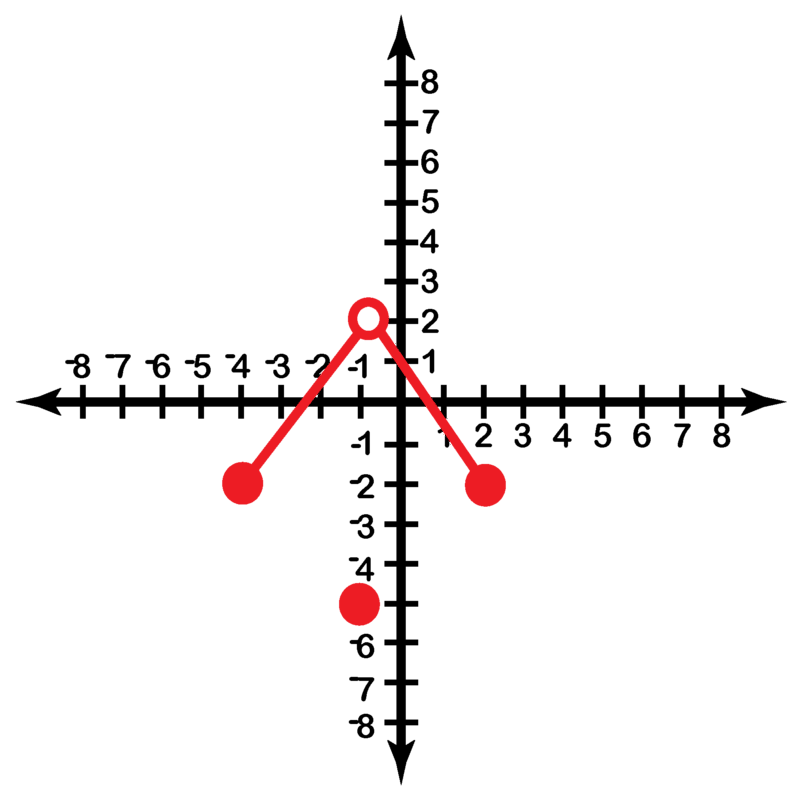
::g(x)x-21对1?

Graph the equation:
::方程式图解 :

This absolute value function has y-values that are paired with more than one x-value, such as (4, 2) and (0, 2). This function is not one-to-one. Note that this function also fails the horizontal line test used in Example 6.
::此绝对值函数的 Y 值配有多个 X 值, 如 (4, 2) 和 (0, 2) 。此函数不是一对一。请注意, 此函数也失败了例6 中使用的水平线测试。

Review
::回顾

Describe the one-to-one horizontal line test.
::描述一对一水平线测试。

Describe the one-to-one algebraic test.
::描述一对一的代数测试。

Which functions are one-to-one?
::哪些功能是一对一?

$\begin{aligned} (3, 28), (4, 29), (4, 30), (6, 31) \end{aligned}$

$\begin{aligned} (4, 5), (9, 6), (7, 8), (23, 5) \end{aligned}$

$\begin{aligned} (8, 18), (33, 4), (5, 16), (7, 19) \end{aligned}$

For the following to be a one-to-one function, x cannot be what values?
::以下函数为一对一函数, x 不能为什么值 ?

$\begin{aligned} (9, 12), (35, 6), (7, 18), (12, X) \end{aligned}$
:9,12),(35,6),(7,18),(12,X)

$\begin{aligned} (20, 21) (21, 14), (110, 112), (X, 7) \end{aligned}$
:20,21,(21,14),(110,112),(X,7))

Are the following one-to-one functions?
::以下是一对一的函数吗?

$\begin{aligned} f (x) = x^{2} \end{aligned}$
:xx)=x2

$\begin{aligned} f (x) = x^{3} \end{aligned}$
:xx)=x3

$\begin{aligned} f (x) = \frac{1}{x} \end{aligned}$
:xx)=1x

$\begin{aligned} f (x) = x^{n} - x, n > 0 \end{aligned}$
:xx)=xn-x,n>0

$\begin{aligned} x = y^{2} + 2 \end{aligned}$
::x=y2+2 x=y2+2

Determine if the relations below are functions, one-to one functions or neither:
::确定以下关系是否为职能、一对一的职能或两者兼有:

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

一对一函数及其逆函数

One-to-One Functions and Their Inverses ::一对一函数及其逆函数

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Example 7 ::例7

Review ::回顾

Review (Answers) ::回顾(答复)

One-to-One Functions and Their Inverses
::一对一函数及其逆函数

Examples
::实例

Example 1
::例1

Example 2
::例2

Example 3
::例3

Example 4
::例4

Example 5
::例5

Example 6
::例6

Example 7
::例7

Review
::回顾

Review (Answers)
::回顾(答复)