Course: 3.3 基本指数函数

Section outline

Select section General

Collapse Expand
General

Collapse all Expand all
- Select activity 新闻通告
  
  新闻通告 Forum

基本指数函数

Can solving an exponential function predict the future? Can be a fast track to wealth?
::解决指数函数能够预测未来吗? 能够快速实现财富吗?

As a matter of fact, yes! Successful entrepreneurs all over the world know the value of modeling population and economic growth and decay. By constructing an accurate exponential equation to model the past and present growth of a particular area of the country, state, or even town, the ideal location for a new business to thrive can be predicted.
::事实上,是的!全世界成功的企业家都知道人口、经济增长和衰退模型的价值。通过构建一个精确的指数式方程式来模拟国家、州甚至城镇某个特定地区的过去和现在的增长,可以预测到新企业兴旺的理想地点。

Some things cannot be modeled of course, such as natural disasters and the like, but often a few well educated guesses make the difference between stunning success and dismal failure in the business world.
::当然,有些事情是无法模拟的,例如自然灾害等等,但往往有一些受过良好教育的猜测在商业界的惊人成功和令人沮丧的失败之间有区别。

Basic Exponential Functions
::基本指数函数

In this lesson you will learn about exponential functions, a family of functions different from the other function families because the variable x is in the exponent . For example, the functions f ( x ) = 2 ^x and g ( x ) = 100(2)5 ^x are exponential functions.
::在此课程中, 您将学习指数函数, 函数组与其他函数组不同, 因为变量 x 在指数中。例如, 函数 f( x) = 2x 和 g( x) = 100(2)5x 是指数函数。

Evaluating Exponential Functions
::评估证据职能

Consider the function f ( x ) = 2 ^x . When we input a value for x , we find the function value by raising 2 to the exponent of x . For example, if x = 3, we have f (3) = 2 ³ = 8.
::考虑函数 f( x) = 2x。当我们输入 x 的值时, 我们通过向 x 的指数加注 2 来找到函数值。例如, 如果 x = 3, 我们有 f(3) = 23 = 8 。

If we choose larger values of x , we will get larger function values, as the function values will be larger powers of 2. For example, f (10) = 2 ¹⁰ = 1,024.
::如果我们选择 x 的较大值, 我们就会得到更大的函数值, 因为函数值将是 2 的较大功率。例如, f(10) = 210 = 1,024 。

If we choose smaller values of x , we will quickly end up with fractions. For instance, if x = 0 , we have f (0) = 2 ⁰ = 1. If x = -3, we have $\begin{aligned} f (- 3) = 2^{- 3} = {(\frac{1}{2})}^{3} = \frac{1}{8} \end{aligned}$ . If we choose smaller and smaller x values, the function values will be smaller and smaller fractions. For example, if x = -10, we have $\begin{aligned} f (- 10) = 2^{- 10} = {(\frac{1}{2})}^{10} = \frac{1}{1024} \end{aligned}$ . Notice that none of the x values we choose will result in a function value of "0", because the numerator of the fraction will always be 1. This tells us that while the domain of this function is the set of all real numbers, the range is limited to the set of positive real numbers.
::如果我们选择 x 的较小值, 我们就会很快以分数结束。例如, 如果 x = 0, 我们就会有 f( 0) = 20 = 1. 如果 x = - 3, 我们就会有 f( 3) = 2- 3 = ( 12) 3 = 18 。如果我们选择较小和小 x 值, 函数值将是较小和小分数。例如, 如果 x = - 10, 我们就会有 f( 10) = 2- 10 = ( 12) 10 = 11024 。请注意, 我们选择的 x 值不会产生 " 0 " 的函数值, 因为分数的计算器总是为 1 。这告诉我们, 虽然此函数的域是所有实际数的集合, 但范围限于正数的组。

In general, if we have a function of the form f ( x ) = a ^x , where a is a positive real number , the domain of the function is the set of all real numbers, and the range is limited to the set of positive real numbers. This restricted domain will result in a specific shape of the graph.
::一般而言,如果我们有一个 f(x) = ax 的函数, 即一个正数为正数的表 f(x) = ax, 函数的域是所有实际数的一组, 范围限于正数的一组。这个限制域将导致图形的具体形状。

Solving Exponential Equations
::解决指数等号

Solving an exponential equation means determining the value of x for a given function value. The solution to the equation 2 ^x = 8 is the value of x that makes the equation a true statement, therefore x = 3, since 2 ³ = 8.
::解析指数方程式意味着确定给定函数值的 x 值。方程式 2x = 8 的解决方案是使方程式成为真实语句的 x 值, 因此 x = 3, 因为23 = 8 。

Examples
::实例

Example 1
::例1

Solve for x : 3 (2 ^x ^{+ 1} ) = 24.
::x: 3(2x+1)=24。

We can solve this equation by writing both sides of the equation as a power of 2:
::我们可以通过将等式的两面写成 2 的能量来解答这个等式:

\begin{aligned} 3 (2^{x + 1}) = 24 \end{aligned}

\begin{aligned} \frac{3 (2^{x + 1})}{3} = \frac{24}{3} \end{aligned}

\begin{aligned} 2^{x + 1} = 8 \end{aligned}

\begin{aligned} 2^{x + 1} = 2^{3} \end{aligned}

To solve the equation now, recall a property of exponents: if b ^x = b ^y , then x = y . That is, if two powers of the same base are equal, the exponents must be equal. This property tells us how to solve:
::要解析方程式, 请记住一个指数属性 : 如果 bx = by, 那么 x = y 。也就是说, 如果同一基础的两个权力相等, 指数必须相等。此属性告诉我们如何解答 :

\begin{aligned} 2^{x + 1} = 2^{3} \end{aligned}

\begin{aligned} \Rightarrow x + 1 = 3 \end{aligned}

\begin{aligned} x = 2 \end{aligned}

Example 2
::例2

For the function g ( x ) = 3 ^x , find g (2), g (4), g (0), g (-2), g (-4).
::函数 g( x) = 3x, 参见 g(2), g(4), g(0), g( 2), g( 4) 。

$\begin{aligned} g (2) = 3^{2} = 9 \end{aligned}$
::g(2)=32=9

$\begin{aligned} g (4) = 3^{4} = 81 \end{aligned}$
::g(4)=34=81

$\begin{aligned} g (0) = 3^{0} = 1 \end{aligned}$
::g( 0)=30=1

$\begin{aligned} g (- 2) = 3^{- 2} = \frac{1}{3^{2}} = \frac{1}{9} \end{aligned}$
::g(-2)=3-2=132=19

$\begin{aligned} g (- 4) = 3^{- 4} = \frac{1}{3^{4}} = \frac{1}{81} \end{aligned}$
::g(-4)=3-4=134=181

The values of the function g ( x ) = 3 ^x behave much like those of f ( x ) = 2 ^x : if we choose larger values, we get larger and larger function values. If x = 0, the function value is 1. And, if we choose smaller and smaller x values, the function values will be smaller and smaller fractions. Also, the range of g ( x ) is limited to positive values.
::函数 g(x) = 3x 的值与 f(x) = 2x 的值相似:如果我们选择更大的值,我们就会得到更大的函数值。如果 x = 0,函数值为 1。如果我们选择小于和小于 x 的值,函数值将是小于和小于分数。此外, g(x) 的范围仅限于正值。

Example 3
::例3

Use a graphing utility to solve each equation.
::使用图形化工具解析每个方程式。

2 ³ ^x ^{- 1} = 7
::23x-1=7

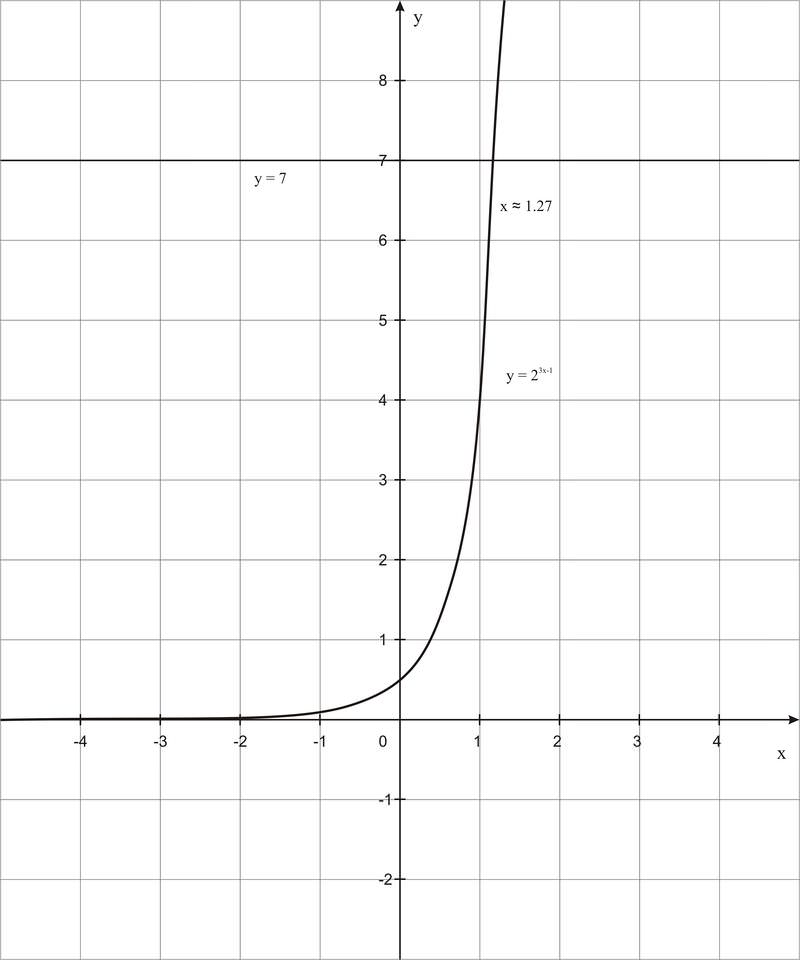
Graph the function y = 2 ³ ^x ^{- 1} and find the point where the graph intersects the horizontal line y = 7. The solution is x ≈ 1.27.
::图形 y = 23x-1, 并找到图形交叉水平线y = 7. 的点, 答案是 x = 1. 27。

6 ^-4 ^x = 2 ⁸ ^x ^{- 5}
::6-4x=28x-5

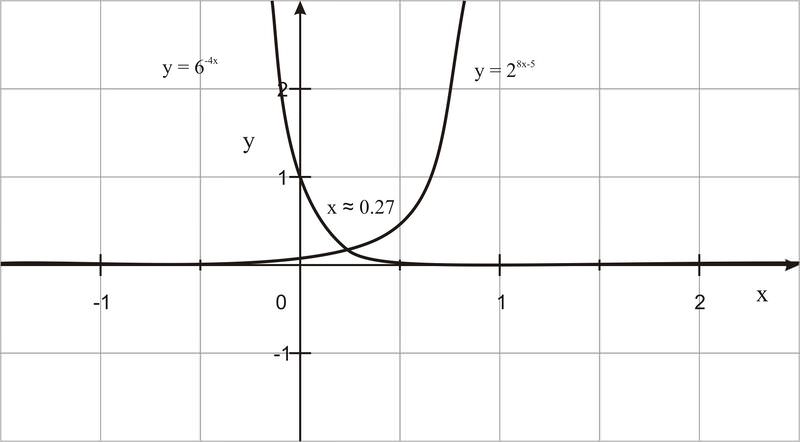
Graph the functions y = 6 ^-4 ^x and y = 2 ⁸ ^x ^{- 5} and find their intersection point.
::函数 y = 6-4x 和 y = 28x- 5, 并找到它们的交叉点。

The solution is approximately x ≈ 0.27. (Your graphing calculator should show 9 digits: 0.272630365.)
::溶液大约 x 0.27。 (您的图形计算器应显示 9位数 : 0.27630365。 )

Example 4
::例4

Graph $\begin{aligned} f (x) = 2^{x} \end{aligned}$ by creating a value table.
::图f(x)=2x,通过创建值表。

First, create a table showing values for x and f(x):
::首先,创建一个表格,显示 x 和 f( x) 的数值:

x	f(x)
(-3)	1/8
(-2)	1/4
(-1)	1/2
0	1
1	2
2	4
3	8

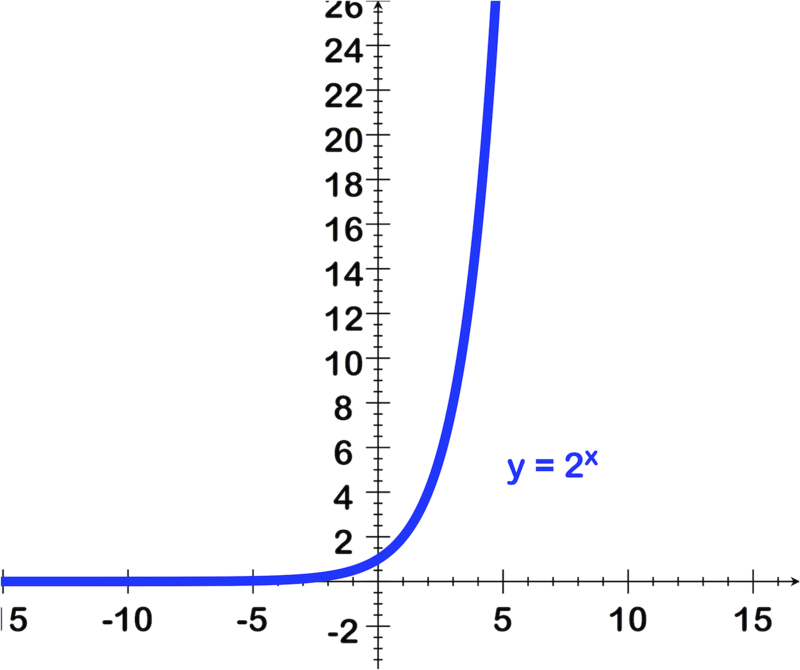
Observe that $\begin{aligned} f \end{aligned}$ is increasing and one-to-one. Also, $\begin{aligned} f \end{aligned}$ is strictly positive and the range of $\begin{aligned} a^{x} \end{aligned}$ is $\begin{aligned} (0, \infty) \end{aligned}$ . Finally, it is important to notice that $\begin{aligned} f (0) = 1 \end{aligned}$ and $\begin{aligned} f (1) = 2 \end{aligned}$ .
::最后,必须注意到,f(0)=1和f(1)=2。

The graph looks like this:
::图表看起来是这样的:

Example 5
::例5

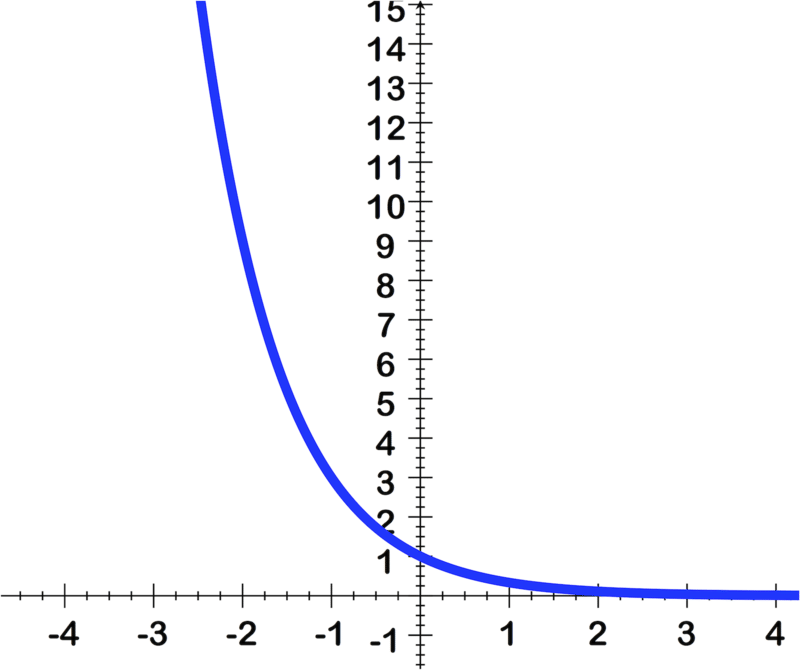
Graph $\begin{aligned} g (x) = (\frac{1}{2})^{x} \end{aligned}$ and explain how it relates to the graph of $\begin{aligned} f (x) = 2^{x} \end{aligned}$ from Example 4 .
::图g(x)=(12)x,并解释它与例4中的f(x)=2x的图形有何关联。

To graph $\begin{aligned} g (x) = (\frac{1}{2})^{x} \end{aligned}$ first consider how it compares to $\begin{aligned} f (x) = 2^{x} \end{aligned}$ from Example 4:
::图g(x)=(12)x首先考虑它与例4中的f(x)=2x的对比:

At first, it looks like a completely new function, but consider:
::首先,它看起来像一个全新的功能,但考虑:

$\begin{aligned} (\frac{1}{2})^{x} = \frac{1}{2^{x}} = 2^{- x} \end{aligned}$
:12x=12x=2-x)

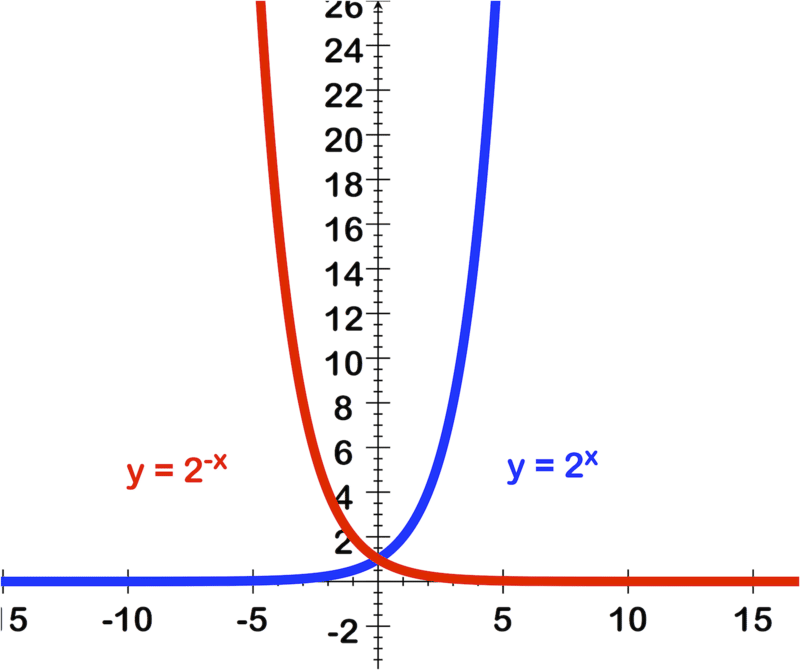
Since $\begin{aligned} 2^{x} \end{aligned}$ is the inverse of $\begin{aligned} 2^{- x} \end{aligned}$ (which could also be written as $\begin{aligned} g (x) = f (- x) \end{aligned}$ ) the graph of $\begin{aligned} g \end{aligned}$ is just the reflection of the graph of $\begin{aligned} f \end{aligned}$ across the y-axis!
::由于 2x 是 2 - x (也可以写成 g( x) =f( - x) ) 的反向, g 的图只是 f 横跨 y 轴的图形的反射 !

The graph below shows $\begin{aligned} f (x) = 2^{x} \end{aligned}$ in blue and $\begin{aligned} g (x) = (\frac{1}{2})^{x} \end{aligned}$ in red:
::下图显示f(x)=2x(蓝色)和g(x)=(12)x(红色):

Example 6
::例6

Solve the equation 5 ⁶ ^x ^{+ 10} = 25 ^x ^{- 1} .
::解决56x+10=25x-1的方程式。

Use the technique explained in the lesson:
::使用课中解释的技巧:

5 ⁶ ^x ^{+ 10} = 25 ^x ^{- 1}
::56x10=25x-1

5 ⁶ ^x ^{+ 10} = (5 ² ) ^x ^{- 1}
::56x10=(52)x-1

5 ⁶ ^x ^{+ 10} = 5 ² ^x ^{- 2}
::56x10=52x-2

$\begin{aligned} \Rightarrow \end{aligned}$ 6 x + 10 = 2 x - 2
::6x + 10 = 2x - 2

4 x + 10 = -2
::4x+10=-2

4 x = -12
::4x = -12

x = -3
::x = -3 = -3

Review
::回顾

Describe an exponential function, and give an example.
::描述指数函数,并举一个例子。

What is an exponential function with increasing outputs known as?
::增加产出的指数函数是什么?

What is an exponential function with outputs that decrease known as?
::产出减少的指数函数是什么?

Evaluate each function at the given value.
::按给定值评价每项功能。

$\begin{aligned} f (x) = \frac{1}{3} \cdot 6^{x} \end{aligned}$ at x = 2
::f(x)=136xxxxx=2

%20%3D%2010%5Ccdot2%5En"> $\begin{aligned} f (n) = 10 \cdot 2^{n} \end{aligned}$ at n = 5
::f=10%2nnnnn=5

$\begin{aligned} g (x) = \frac{1}{5} \cdot (\frac{1}{3})^{x} \end{aligned}$ at x = 3
::g( x) = 15%( 13x x x = 3)

Look at the graph below of the exponential function $\begin{aligned} g (x) = a^{x} \end{aligned}$ . Find $\begin{aligned} a \end{aligned}$
::查看指数函数 g( x) =ax 下方的指数函数 g( x) =ax 的图形。 find a

Sketch the graph of each exponential function and explicitly evaluate each function for at least four values of x:
::绘制每个指数函数的图形,并明确评估每个函数的至少四个x值:

$\begin{aligned} f (x) = π^{x} \end{aligned}$
:fx) x

$\begin{aligned} f (x) = (\frac{2}{3})^{- x} \end{aligned}$
:xx)=(23)-x

$\begin{aligned} f (x) = 2^{x + 4} - 2 \end{aligned}$
:xx)=2x+4-2

Find the average rate of change of $\begin{aligned} f (x) = 2^{x} \end{aligned}$ from $\begin{aligned} x = 3 \end{aligned}$ to $\begin{aligned} x = 6 \end{aligned}$ . Draw a graph that illustrates your answer
::查找 f( x) =2x 从 x=3 到 x=6 的平均变化速率。绘制一个图形, 显示您的答复

HINT for problems 12 - 14:
::针对问题12-14:

$\begin{aligned} A = P (1 + \frac{r}{n})^{n t} \end{aligned}$ where:
::A=P(1+rn)nt, 其中 :

A = ending A mount

P = P rincipal (beginning amount)

r = interest r ate (as a decimal value - NOT as a percentage!)

n = n umber of compoundings per period (commonly one year)

t = t ime (the number of periods/years)

If you invest $28,000 in an account that gets 10% annual interest compounded quarterly, how much would you have in 15 years?
::如果你投资28,000美元在一个账户中, 得到10%的年利息复计季度, 15年内你有多少?

If you invested a penny on Jan 1, 1776 at 12% interest compounded daily, how much would you have on Jan 1, 2013 ?
::如果你在1月1日、1776年1月1日投资一分钱,

How much would you need to invest to get $20,000 in 3 years at an annual interest rate of 6.5% compounded monthly?
::3年内,你需要投资多少钱才能以每月6.5%的年利率获得20,000美元?

The half-life of element -137m is 2.552 minutes. How much of an 10 gram sample would be left after 8 minutes?
::元素-137m的半衰期为2.552分钟,8分钟后将有多少10克样本还剩多少?

The half – life of carbon 14 is 5,730 years. How much of a 100 gram sample would be left after 25,000 years ?
::碳14的半衰期是5,730年。 25,000年后,100克样本中有多少还剩下?

Sketch and use the graphs of $\begin{aligned} f (x) = (\frac{1}{3})^{x} \end{aligned}$ and $\begin{aligned} p (x) = (\frac{1}{4})^{x} \end{aligned}$ to graph the inequality $\begin{aligned} (\frac{1}{3})^{x} \leq g (x) \leq (\frac{1}{4})^{x} \end{aligned}$
::使用 f(x) =( 13) x 和 p(x) =( 14) x 的图解来绘制不平等( 13x) x (x) =( 14) x ) 的图解

Review (Answers)
::回顾(答复)

Click to see the answer key or go to the Table of Contents and click on the Answer Key under the 'Other Versions' option.
::单击可查看答题键, 或转到目录中, 单击“ 其他版本” 选项下的答题键。

Section outline

General

基本指数函数

Basic Exponential Functions ::基本指数函数

Evaluating Exponential Functions ::评估证据职能

Solving Exponential Equations ::解决指数等号

Examples ::实例

Example 1 ::例1

Example 2 ::例2

Example 3 ::例3

Example 4 ::例4

Example 5 ::例5

Example 6 ::例6

Review ::回顾

Review (Answers) ::回顾(答复)